DOCSLIB.ORG

Vation Is Left As an Cise

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Vation Is Left As an Cise 408 Chapter 9 Gas Power Systems 70 60 ~ I=" 50 ,:; u 40 'u"'" .....!.::: 30 0;" E 20 ~ ~ 10 0 5 10 15 20 .... Figure 9.6 Thermal efficiency of the cold air· Compression ralio, r standard Diesel cycle, k = 1.4. where r is the compression ratio and rc the cutoff ratio. The derivation is left as an cise. This relationship is shown in Fig. 9,6 for k = 1.4. Equation 9.13 for the Diesel differs from Eq. 9.8 for the Otto cycle only by the term in brackets, which for " > greater than unity. Thus, when the compression ratio is the same, the thermal the cold air-standard Diesel cycle would be less than that of the cold air-standard cycle. In the next example, we illustrate the analysis of the air-standard Diesel cycle. 1 II. I Q., ~ h 'I ....., ~',"1""": " .} ....I.-J,. l_ L ' ...... h,. "L b~ f .... l. Qt\VJ(",. / 'I".... tl.. ? r -J L...,.., U I'~J l.'''''/',; 1;1' J ... ,," j.,,>-I. '" At the beginning of the compression process of an air-standard Diesel cycle operating with a compression ratio of 18 , the perature is 300 K and the pressure is 0.1 MPa. The cutoC:( ratio for the cycle is 2. Determine (a) the temperature and at the end of each process of the cycle, (b) the thermal ' fficiency, (c) the mean effective pressure, in MPa. SOLUTION f'{UW ~ ' .... m c ..'( J ;(....clv4.. 'j ....;Y'\ j~..ll ~ ; ......'c.. Known: An air-standard Diesel cycle is executed with specified conditions at the beginning of the compression stroke. compression and cutoff ratios are given. Find: Determine the temperature and pressure at the end of each process, the thermal efficiency, and mean pressure. ..I" :J f£! I,..,,"",, ~..... I ., j ell\(.\ Schematic and Given Data: \1) ". 1.... "v'" rr J1. ' PI T I 4 v s .... Figure E9.2 9.J Air-Standard Diesel Cycle 409 the piston- cylinder assembly IS the closed system. 71pre:SSlcm and expimsibn processes are adiabatic. are internally reversible. '1 .la r"'O ,'~/1I 1. V:,,~""'\. modeled as an ideal gas. ~ potential energy effects are negligible. J) T~!J.., L1l"-, / . ' LJrv::.I1-T .4T.J<:, /ot1 -lillt;/v vr - JJ'" 1::: begins by detemtining proRMJies-at each_prin.cipal state of the cycle. With Tl = 300 K, Table ~giVeS ( " t.,h and vrI = 621 .2. For tl e isentropic compression process 1-2 _ I. ~ I ') L -r DP 0/ f ~ ?I~ if; r 6"'I • IJ' (: .l ,.,.. Y V2 Vrl 621.2 - :: ~ - I, 2 J - I It "1. Va = -v I = ­ = -­= 34.51 Y. v.. it" 1 '<J " "'-' T ' V r r 18 ~ - 1, v '-' 1 I ~ ~ • , V'­ , Vr - ~,I l in Tab~ we get T2 = 898.3 K and h2 = 930.98 kJ/kg. With ~ ideal g a on of state I • I • A r -; ~ f) tJ -~- - -----" _ . _ T2 VI _ (898.3~ _ 1­ '-, j~ r: '! :. P, i'!.L.,- Ii P2 - PI V - (0.1) 300 (18) - 5.39 MPa , , ~, tJ • ..A.- ~ 'j..:.-r , " . Tl 2 , r ~ .:. -;' I 1. ~ 'hI (. .' " . ' r"~ '" " e,I , . • at state 2 can be evaluated alternatively lising the isentrHpic relationship, P2 ' =' P'I'(Pr2/PrI)' .i ~ (1 ) e. ?rocess 2-3 occurs at constant pressure, the ideal gas equation of state gives 11-, ilJ'} .J; ~ )( f8 _ __1_ - ~ J..JJ"I "<- WI.' 11 ~I__ V3 t! 1,Ji J ('J. - :F,t~l T3 = -T2 ~7o . V2 17 I.: I,,~ . .k;4j • -,J •• '" t L("I-n~.L , ." I ~ .. r'1 , ... l. the compression ratio r, and ~e cutoff ratio re, we have r~~ t::V~ ~8 _ J.t(?/"'): L V) V,4 - Vr3 - . ) - 35.73 l. p-1, (... -:; VI. ('1" fd~l. J w,'!..., in Table .~ with Vr4' we get li4 =.§.64d1OTkg and T4 =~ K. The pressure at state 4 can be found using N ~)- , relationship P4 = P3(Pr4/Pr3 ) or the ideal gas equation of state applied at states 1 and 4. With V~= V, the ideal bl.... v"dJ of state gives 8- ~/fL JCJ.. MP"I 'I, .. .. ~ LIt.... (J I, ,-, ' V P.. PI T. (0.1 MPa) = = (~ K) = n ~J a 1~.'; ~~ , TI \ 300 K 7 "" therrnai efficiency is found using , ~ CJ"... f-­ 'Y/ = 1- Q4Jm =['1 __ ~li. - lil ) J> Q23/m h3 - h2 ~ 664.3 - 214.07 = 1 - 1999.1 _ 930.98 = 0.578 (57.8%) mean effective pressure written in terms of specific volumes is 41 0 Chapter 9 Gas Power Systems The net work of the cycle equals the net heat added [w . ~.= ;;J ~ycle Q23 Q41 . ... -- = - - - = (h3 - h2) - (U4 - Ul) m m Tn = (1999.1 - 930.98) - ~- 214.07) = ~ kJ/kg ' 1k1 ,J The specific volume at state 1 is 'lO,i,) j r.\~1.> ~ _., 8314 N· (300 K) ( m) 28.97 kg . K _ 3 5 2 - 0.861 m /kg t. lON/m ...... ,Jf'Jjn Inserting values ~ ~ \)"1 -::. ­ t~.:h. 0'I me _ ~/kg 1103 N . mill MPa I '~ ~ "'In 'to 3 2 p - 0,861(1, - 1/18) m /kg 1 kJ 106 N/m - ~ ftI ''y ( d ~ I():I .... = 0.76 MPa 0, 'J) b f kt' ,. It) lit '''' 1. o This solution uses the air tables, which account explicitly for the variation of the specific heats with that Eg. 9.13 based onthe assumption of constant specific heats has not been used to determine the thennal The cold air-standard solution of this example is left as an exercise. Air-Standard Dual Cycle The pressure-volume diagrams of actual internal combustion engines are not well by the Otto and Diesel cycles. An air-standard cycle that can be made to dual cycle the pressure variations more closely is the air-standard dual cycle. The dual cycle is in Fig. 9.7. As in the Otto and Diesel cycles, Process 1-2 is an isentropic The heat addition occurs in two steps, however: Process 2~ 3 is a constant-volume dition; Process 3-4 is a constant-pressure heat addition. Process 3- 4 also fIrst part of the power stroke. The isentropic expansion from state 4 to state 5 is .. mainder of the power stroke. As in the Otto and Diesel cycles, the cycle is a constant-volume heat rejection process, Process 5-1. Areas on the T-s and p-u can be interpreted as heat and work, respectivel)', as in the cases of the Otto c'lc\e';',. P 3 T 4 2 p=c 3 v = c 5 2 v =c v A. Figure 9.7 p-v and T-s diagrams of the air-standard dual cycle. 0.4 Air-Standard Dual Cycle 4 I I Since the dual cycle is composed of the same types of processes as the Diesel cycles, we can simply write down the appropriate work and heat transfer ex­ by reference to the corresponding earlier developments. Thus, during the isentropic process 1-2 there is no heat transfer, and the work is W l2 --;;; = 11 2 - III the corresponding process of the Otto cycle, in the constant-volume portion of the process, Process 2-3, there is no work, and the heat transfer is Q23 -;;; = u3 ­ U2 constant-pressure portion of the heat addition process, Process 3-4, there is both work transfer, as for the corresponding process of the Diesel cycle and the isentropic expansion process 4-5 there is no heat transfer, and the work is W45 --;;; = 114 - U5 the constant-volume heat rejection process 5-1 that completes the cycle involves but no work thennal efficiency is the ratio of the net work of the cycle to the total heat added WCYcl Jm Q51/m 1/ = = 1 - ----=.;:.--­ (Q2i m + Q 3~m) (Q2im + Q34/m ) (u 5 - Ul) = 1 - ---'------ (9 .14) I (113 - U2 ) + (h 4 - h3) ., example to follow provides an illustration of the analysis of an air-standard dual cycle. exhibits many of the features found in the Otto and Diesel cycle examples previously. ihe beginning of the compression process of an air-standard dual cycle with a compression ratio of 18, the temperature is K and the pressure is 0.1 MPa. The pressure ratio for the constant volume part of the heating process is 1.5:1. The vol­ ratio for the constant pressure part of the heating process is 1.2:1. Determine (a) the thermal efficiency and (b) the mean . An air-standard dual cycle is executed in a piston-cylinder assembly. Conditions are known at the beginning of the : om~)res~;ion' process, and necessary volume and pressure ratios are specified. Determine the thermal efficiency and the mep, in MPa. 4 ! 2 Chapter 9 Gas Power Systems Schematic and Giv.en DaJa: p --- } T 2 5 2 , - -7 =300K 1 1 v 5 .... Figure E9.3 AssumptWns: 1. The air in the piston-cylinder assembly is the closed system. 2. The compression and expansion processes are adiabatic. I 3. All processes are internally reversible. J o :> ~ I ",' ., PI _11 (. , I t 4. The air is modeled as an ideal gas. (;, :; 2.flrl (J1 Vr. = 62.1, 2.. S. Kinetic and potential energy effects are negligible. I 1 V'r 2 bJ('I'L ~ 1'1,s Analysis: The analysis begins by determining properties at each principal state of the cycle. States 1 and 2 are the same in Example 9.2. so UI = 214.07 kJ/kg, Tz = 898.3 K, U? = 673.2 kJ/kg. Since Process 2-3 occurs at constant volume, ideal gas equation of state reduces to give Y,...,-- ""J;I,'1 Ii.
Load more

Recommended publications
  • Steady State and Transient Efficiencies of A
    STEADY STATE AND TRANSIENT EFFICIENCIES OF A FOUR CYLINDER DIRECT INJECTION DIESEL ENGINE FOR IMPLEMENTATION IN A HYBRID ELECTRIC VEHICLE A Thesis Presented to The Graduate Faculty of The University of Akron In Partial Fulfillment of the Requirements for the Degree Masters of Science Charles Van Horn August, 2006 STEADY STATE AND TRANSIENT EFFICIENCIES OF A FOUR CYLINDER DIRECT INJECTION DIESEL ENGINE FOR IMPLEMENTATION IN A HYBRID ELECTRIC VEHICLE Charles Van Horn Thesis Approved: Accepted: Advisor Department Chair Dr. Scott Sawyer Dr. Celal Batur Faculty Reader Dean of the College Dr. Richard Gross Dr. George K. Haritos Faculty Reader Dean of the Graduate School Dr. Iqbal Husain Dr. George R. Newkome Date ii ABSTRACT The efficiencies of a four cylinder direct injection diesel engine have been investigated for the implementation in a hybrid electric vehicle (HEV). The engine was cycled through various operating points depending on the power and torque requirements for the HEV. The selected engine for the HEV is a 2005 Volkswagen 1.9L diesel engine. The 2005 Volkswagen 1.9L diesel engine was tested to develop the steady-state engine efficiencies and to evaluate the transient effects on these efficiencies. The peak torque and power curves were developed using a water brake dynamometer. Once these curves were obtained steady-state testing at various engine speeds and powers was conducted to determine engine efficiencies. Transient operation of the engine was also explored using partial throttle and variable throttle testing. The transient efficiency was compared to the steady-state efficiencies and showed a decrease from the steady- state values.
    [Show full text]
  • Thermodynamics of Power Generation
    THERMAL MACHINES AND HEAT ENGINES Thermal machines ......................................................................................................................................... 1 The heat engine ......................................................................................................................................... 2 What it is ............................................................................................................................................... 2 What it is for ......................................................................................................................................... 2 Thermal aspects of heat engines ........................................................................................................... 3 Carnot cycle .............................................................................................................................................. 3 Gas power cycles ...................................................................................................................................... 4 Otto cycle .............................................................................................................................................. 5 Diesel cycle ........................................................................................................................................... 8 Brayton cycle .....................................................................................................................................
    [Show full text]
  • Review of the Fundamentals Thermal Sciences
    Review of the Fundamentals Reading Problems Review Chapter 3 and property tables More specifically, look at: 3.2 ! 3.4, 3.6, 3.7, 8.4, 8.5, 8.6, 8.8 Thermal Sciences The thermal sciences involve the storage, transfer and conversion of energy. Thermodynamics HeatTransfer Conservationofmass Conduction Conservationofenergy Convection Secondlawofthermodynamics Radiation HeatTransfer Properties Conjugate Thermal Thermodynamics Systems Engineering FluidsMechanics FluidMechanics Fluidstatics Conservationofmomentum Mechanicalenergyequation Modeling Thermodynamics: the study of energy, energy transformations and its relation to matter. The anal- ysis of thermal systems is achieved through the application of the governing conservation equations, namely Conservation of Mass, Conservation of Energy (1st law of thermodynam- ics), the 2nd law of thermodynamics and the property relations. Heat Transfer: the study of energy in transit including the relationship between energy, matter, space and time. The three principal modes of heat transfer examined are conduction, con- vection and radiation, where all three modes are affected by the thermophysical properties, geometrical constraints and the temperatures associated with the heat sources and sinks used to drive heat transfer. Fluid Mechanics: the study of fluids at rest or in motion. While this course will not deal exten- sively with fluid mechanics we will be influenced by the governing equations for fluid flow, namely Conservation of Momentum and Conservation of Mass. 1 Examples of Energy Conversion windmills
    [Show full text]
  • Performance Analysis of a Diesel Cycle Under the Restriction of Maximum Cycle Temperature with Considerations of Heat Loss, Friction, and Variable Specific Heats S.S
    Vol. 120 (2011) ACTA PHYSICA POLONICA A No. 6 Performance Analysis of a Diesel Cycle under the Restriction of Maximum Cycle Temperature with Considerations of Heat Loss, Friction, and Variable Specific Heats S.S. Houa;¤ and J.C. Linb aDepartment of Mechanical Engineering, Kun Shan University, Tainan City 71003, Taiwan, ROC bDepartment of General Education, Transworld University, Touliu City, Yunlin County 640, Taiwan, ROC (Received November 11, 2010) The objective of this study is to examine the influences of heat loss characterized by a percentage of fuel’s energy, friction and variable specific heats of working fluid on the performance of an air standard Diesel cycle with the restriction of maximum cycle temperature. A more realistic and precise relationship between the fuel’s chemical energy and the heat leakage that is constituted on a pair of inequalities is derived through the resulting temperature. The variations in power output and thermal efficiency with compression ratio, and the relations between the power output and the thermal efficiency of the cycle are presented. The results show that the power output as well as the efficiency where maximum power output occurs will increase with the increase of maximum cycle temperature. The temperature-dependent specific heats of working fluid have a significant influence on the performance. The power output and the working range of the cycle increase while the efficiency decreases with increasing specific heats of working fluid. The friction loss has a negative effect on the performance. Therefore, the power output and efficiency of the cycle decrease with increasing friction loss. It is noteworthy that the effects of heat loss characterized by a percentage of fuel’s energy, friction and variable specific heats of working fluid on the performance of a Diesel-cycle engine are significant and should be considered in practice cycle analysis.
    [Show full text]
  • Air Standard Assumptions Some Definitions for Reciprocation Engines
    Air Standard Assumptions In power engines, energy is provided by burning fuel within the system boundaries, i.e., internal combustion engines. The following assumptions are commonly known as the air- standard assumptions: 1- The working fluid is air, which continuously circulates in a closed loop (cycle). Air is considered as ideal gas. 2- All the processes in (ideal) power cycles are internally reversible. 3- Combustion process is modeled by a heat-addition process from an external source. 4- The exhaust process is modeled by a heat-rejection process that restores the working fluid (air) at its initial state. Assuming constant specific heats, (@25°C) for air, is called cold-air-standard assumption. Some Definitions for Reciprocation Engines: The reciprocation engine is one the most common machines that is being used in a wide variety of applications from automobiles to aircrafts to ships, etc. Intake Exhaust valve valve TDC Bore Stroke BDC Fig. 3-1: Reciprocation engine. Top dead center (TDC): The position of the piston when it forms the smallest volume in the cylinder. Bottom dead center (BDC): The position of the piston when it forms the largest volume in the cylinder. Stroke: The largest distance that piston travels in one direction. Bore: The diameter of the piston. M. Bahrami ENSC 461 (S 11) IC Engines 1 Clearance volume: The minimum volume formed in the cylinder when the piston is at TDC. Displacement volume: The volume displaced by the piston as it moves between the TDC and BDC. Compression ratio: The ratio of maximum to minimum (clearance) volumes in the cylinder: V V r max BDC Vmin VTDC Mean effective pressure (MEP): A fictitious (constant throughout the cycle) pressure that if acted on the piston will produce the work.
    [Show full text]
  • Machinery/Automation
    Machinery/Automation Miniature Blimps for Surveillance and Collection of Samples These robots could follow complex three-dimensional trajectories through buildings. NASA’s Jet Propulsion Laboratory, Pasadena, California Miniature blimps are under develop- structures on Earth. The widely per- 1.2 kg. It can be filled in 30 seconds ment as robots for use in exploring the ceived need for means to thwart attacks from the small bottle shown on the thick, cold, nitrogen atmosphere of Sat- on buildings and to mitigate the effects table in the figure. This blimp also op- urn’s moon, Titan. Similar blimps can of such attacks has prompted considera- erates under radio control and carries a also be used for surveillance and collec- tion of the use of robots. Relative to video camera. This blimp has been tion of biochemical samples in build- “rover”-type (wheeled) robots that have equipped with an ultralight (170 g) au- ings, caves, subways, and other, similar been considered for such uses, minia- tomatic pilot manufactured commer- ture blimps offer the advantage of abil- cially for radio-controlled small air- ity to move through the air in any direc- planes. This autopilot enables the tion and, hence, to perform tasks that control system of the blimp to utilize are difficult or impossible for wheeled the Global Positioning System in fol- robots, including climbing stairs and lowing a trajectory through as many as looking through windows. In addition, 60 different waypoints. This autopilot miniature blimps are expected to have also utilizes ultrasound for precise mea- greater range and to cost less, relative to surement and control of altitude when wheeled robots.
    [Show full text]
  • Thermodynamic Data
    ..................................APPENDIX A Thermodynamic data A.l Introduction The thermodynamic tables presented here for enthalpy and internal energy differ from those that are usually available, since they incorporate the enthalpy of formation. This means that there is no need for separate tabulations of calorific values, and it will be found that energy balances for combustion calculations are greatly simplified. The enthalpy of formation (t-.Hf) is perhaps more familiar to physical chemists than to engineers. The enthalpy of formation ( t-.Hf) of a substance is the standard reaction enthalpy for the formation of the compound from its elements in their reference state. The reference state of an element is its most stable state (for example, carbon atoms, but oxygen molecules) at a specified temperature and pressure, usually 298.15 K and a pressure of l bar. In the case of atoms that can exist in different forms, it is necessary to specify their form, for example, carbon is as graphite, not diamond. Combustion calculations are most readily undertaken by using absolute (some­ times known as sensible) internal energies or enthalpy. In steady-flow systems where there is displacement work then enthalpy should be used; this has been illustrated by figure 3.8. When there is no displacement work then internal energy should be used (figure 3.7). Consider now figure 3.8 in more detail. With an adiabatic combustion process from reactants (R) to products (P) the enthalpy is constant, but there is a substantial rise in temperature: (A.l) In the case of the isothermal combustion process (IR ~ IP) the temperature (T) is obviously constant, and the difference in enthalpy corresponds to the isobaric calorific value (-t-.Jfi,): t-.H~ = HR .T- HP,T (A.2) 582 Thermodynamic data A.2 Thermodynamic principles In the following sections, it will be seen how the thermodynamic data for internal energy, enthalpy, entropy and Gibbs function can all be determined from measurements of heat capacity and phase change enthalpies (or internal energies).
    [Show full text]
  • Power Plant 3
    Centre of Excellence in Renewable Energy Education and Research, New Campus, University of Lucknow, Lucknow B Voc. Renewable Energy Technology Semester II First Year Module RET-203: Power Plant Engineering Unit-2 (Air Standard cycle and Diesel Electric Power Plant) Contents: Internal Combustion Engine and External Combustion Engine: Otto Cycle, Diesel Cycle, Dual Cycle, Efficiency and Indicator Diagram. Diesel Electric Power Plant: Working Principle, Layout, Performance and Thermal Efficiency, Combined Cycle Power Plant, Layout, Efficiency. Internal Combustion Engine and External Combustion Engine In an external combustion engine, the fuel isn't burned inside the engine. With an internal combustion engine, the combustion chamber lies right in the middle of the engine. An Internal combustion engines rely on the explosive power of the fuel within the engine to produce work. In internal combustion engines, the explosion forcefully pushes pistons or expels hot high-pressure gas out of the engine at great speeds. Both moving pistons and ejected high- speed gas have the ability to do work. In external combustion engines, combustion heats a fluid which, in turn, does all the work. Example: Atkinson, Brayton/Joule, Diesel, Otto, Gas Generator etc. An external combustion engine uses a working fluid, either a liquid or a gas or both, that is heated by a fuel burned outside the engine. The external combustion chamber is filled with a fuel and air mixture that is ignited to produce a large amount of heat. This heat is then used to heat the internal working fluid either through the engine wall or a heat exchanger. The fluid expands when heated, acting on the mechanism of the engine, thus producing motion and usable work.
    [Show full text]
  • Simulations of Compressible Flows Associated with Internal Combustion
    Simulations of compressible flows associated with internal combustion engines by Olle Bodin February 2013 Technical Reports from Royal Institute of Technology KTH Mechanics SE-100 44 Stockholm, Sweden Akademisk avhandling som med tillst˚andav Kungliga Tekniska H¨ogskolan i Stockholm framl¨aggestill offentlig granskning f¨oravl¨aggandeav teknologie doktorsexamen Fredagen den 8/2 2013 kl 10:00 i sal F3, Lindstedtsv¨agen26, Kungliga Tekniska H¨ogskolan, Vallhallav¨agen79, Stockholm. ⃝c Olle Bodin 2013 Universitetsservice US{AB, Stockholm 2013 Simulations of compressible flows associated with internal combustion engines Olle Bodin 2013, KTH Mechanics SE-100 44 Stockholm, Sweden Abstract Vehicles with internal combustion (IC) engines fueled by hydrocarbon com- pounds have been used for more than 100 years for ground transportation. During these years and in particular the last decade, the environmental as- pects of IC engines have become a major political and research topic. Follow- ing this interest, the emissions of pollutants such as NOx, CO2 and unburned hydrocarbons (UHC) from IC engines have been reduced considerably. Yet, there is still a clear need and possibility to improve engine efficiency while further reducing emissions of pollutants. The maximum efficiency of IC engines used in passenger cars is no more than 40% and considerably less than that under part load conditions. One way to improve engine efficiency is to utilize the energy of the exhaust gases to turbocharge the engine. While turbocharging is by no means a new concept, its design and integration into the gas exchange system has been of low priority in the power train design process. One expects that the rapidly increasing interest in efficient passenger car engines would mean that the use of turbo technology will become more widespread.
    [Show full text]
  • Module I BASIC THERMODYNAMICS REFERENCES: ENGINEERING THERMODYNAMICS by P.K.NAG 3RD EDITION LAWS of THERMODYNAMICS
    Module I BASIC THERMODYNAMICS REFERENCES: ENGINEERING THERMODYNAMICS by P.K.NAG 3RD EDITION LAWS OF THERMODYNAMICS • 0 th law – when a body A is in thermal equilibrium with a body B, and also separately with a body C, then B and C will be in thermal equilibrium with each other. • Significance- measurement of property called temperature. A B C Evacuated tube 100o C Steam point Thermometric property 50o C (physical characteristics of reference body that changes with temperature) – rise of mercury in the evacuated tube 0o C bulb Steam at P =1ice atm T= 30oC REASONS FOR NOT TAKING ICE POINT AND STEAM POINT AS REFERENCE TEMPERATURES • Ice melts fast so there is a difficulty in maintaining equilibrium between pure ice and air saturated water. Pure ice Air saturated water • Extreme sensitiveness of steam point with pressure TRIPLE POINT OF WATER AS NEW REFERENCE TEMPERATURE • State at which ice liquid water and water vapor co-exist in equilibrium and is an easily reproducible state. This point is arbitrarily assigned a value 273.16 K • i.e. T in K = 273.16 X / Xtriple point • X- is any thermomertic property like P,V,R,rise of mercury, thermo emf etc. OTHER TYPES OF THERMOMETERS AND THERMOMETRIC PROPERTIES • Constant volume gas thermometers- pressure of the gas • Constant pressure gas thermometers- volume of the gas • Electrical resistance thermometer- resistance of the wire • Thermocouple- thermo emf CELCIUS AND KELVIN(ABSOLUTE) SCALE H Thermometer 2 Ar T in oC N Pg 2 O2 gas -273 oC (0 K) Absolute pressure P This absolute 0K cannot be obtatined (Pg+Patm) since it violates third law.
    [Show full text]
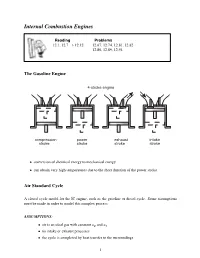
  • Internal Combustion Engines
    Internal Combustion Engines Reading Problems 12.1, 12.7 ! 12.12 12.67, 12.74, 12.81, 12.82 12.86, 12.89, 12.94 The Gasoline Engine • conversion of chemical energy to mechanical energy • can obtain very high temperatures due to the short duration of the power stroke Air Standard Cycle A closed cycle model for the IC engine, such as the gasoline or diesel cycle. Some assumptions must be made in order to model this complex process. ASSUMPTIONS: • air is an ideal gas with constant cp and cv • no intake or exhaust processes • the cycle is completed by heat transfer to the surroundings 1 • the internal combustion process is replaced by a heat transfer process from a TER • all internal processes are reversible • heat addition occurs instantaneously while the piston is at TDC Definitions Mean Effective Pressure (MEP): The theoretical constant pressure that, if it acted on the piston during the power stroke would produce the same net work as actually developed in one complete cycle. net work for one cycle W MEP = = net displacement volume VBDC − VT DC The mean effective pressure is an index that relates the work output of the engine to it size (displacement volume). Otto Cycle • the theoretical model for the gasoline engine • consists of four internally reversible processes • heat is transferred to the working fluid at constant volume Otto Cycle Efficiency W Q − Q Q Q η = net = H L = 1 − L = 1 − 4−1 QH QH QH Q2−3 QH = mcv(T3 − T2)(intake) QL = mcv(T4 − T1)(exhaust) Therefore ! T4 ! − 1 (T4 − T1) T1 T1 η = 1 − = 1 − ! (T − T ) T T3 3 2 2 − 1 T2 2 Since
    [Show full text]
  • Thermodynamic Cycles • Look at Different Cycles That Approximate Real Processes • You Can Categorize These Processes Several Different Ways • Power Cycles Vs
    Thermodynamic Cycles • Look at different cycles that approximate real processes • You can categorize these processes several different ways • Power Cycles vs. Refrigeration • Gas vs. Vapor • Closed vs. open • Internal Combustion vs. External Combustion Power Cycles • Otto Cycle • Spark Ignition • Diesel Cycle • Brayton Cycle • Gas Turbine •RankineCycle These are all heat engines. They convert heat to work, so the efficiency is: Wnet ηth = Qin Ideal Cycles • We’ll be using ideal cycles to analyze real systems, so lets start with the only ideal cycle we’ve studied so far Carnot Cycle W Q Q-W=0 Æ Q=W In addition, we know that the efficiency for a Carnot Cycle is: TL ηth, Carnot =−1 TH Carnot Cycle is not a good model for most real processes • For example • Internal combustion engine •Gas turbine • We need to develop a new model, that is still ideal Air-Standard Assumptions • Air continuously circulates in a closed loop and behaves as an ideal gas • All the processes are internally reversible • Combustion is replaced by a heat- addition process from the outside • Heat rejection replaces the exhaust process • Also assume a constant value for Cp, evaluated at room temperature Terminology for Reciprocating Devices V max V Compression Ratio r ==BDC V min VTDC Mean Effective Pressure 2 W = PdV ∫1 W = P∆V v v 1-2 Isentropic Compression 2-3 Constant Volume Heat Addition 3-4 Isentropic Expansion 4-1 Constant Volume Heat Rejection Thermal Efficiency of the Otto Cycle Wnet Qnet QQin− out Qout ηth === =−1 Qin Qin Qin Qin Apply First Law Closed System
    [Show full text]