DOCSLIB.ORG

Papr Reduction in OFDM Communications with Generalized

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Papr Reduction in OFDM Communications with Generalized Copyright Warning & Restrictions The copyright law of the United States (Title 17, United States Code) governs the making of photocopies or other reproductions of copyrighted material. Under certain conditions specified in the law, libraries and archives are authorized to furnish a photocopy or other reproduction. One of these specified conditions is that the photocopy or reproduction is not to be “used for any purpose other than private study, scholarship, or research.” If a, user makes a request for, or later uses, a photocopy or reproduction for purposes in excess of “fair use” that user may be liable for copyright infringement, This institution reserves the right to refuse to accept a copying order if, in its judgment, fulfillment of the order would involve violation of copyright law. Please Note: The author retains the copyright while the New Jersey Institute of Technology reserves the right to distribute this thesis or dissertation Printing note: If you do not wish to print this page, then select “Pages from: first page # to: last page #” on the print dialog screen The Van Houten library has removed some of the personal information and all signatures from the approval page and biographical sketches of theses and dissertations in order to protect the identity of NJIT graduates and faculty. ASAC A EUCIO I OM COMMUICAIOS WI GEEAIE ISCEE OUIE ASOM b Srt Sn h n dvnt f Gnrlzd rt rr rnfr (G t blt t dn d ltn f ntnt dl rthnl d t bd n th drd prfrn tr n th nnrn p f ntrt On f th n drb f Orthnl rn vn Mltplxn (OM t th hh t Avr r t (A vl hh drtl rltd t pr nptn f th t rt rr rnfr ( prd OM thnl l nn Snl Crrr rn vn Mltpl A (SCMA hh h lr A vl d fr pln hnnl In th th th A f prd OM frthr drd b n G npt h prfrn prvnt f G bd A rdtn fr vr SCMA ntn nr r vltd b ltn rfrn ltn rlt hd tht A ffn f SCMA t fr nr h Shft Kn (SK Qdrtr h Shft Kn (QSK nd 1 Qdrtr Apltd Mdltn (1-QAM dtl dltn thn r nrd A EUCIO I OM COMMUICAIOS WI GEEAIE ISCEE OUIE ASOM b Srt Sn A h Sbttd t th lt f r Inttt f hnl n rtl lfllnt f th rnt fr th r f Mtr f Sn n Eltrl Ennrn prtnt f Eltrl nd Cptr Ennrn M 1 APPROVAL PAGE PAPR REDUCTION IN OFDM COMMUNICATIONS WITH GDFT Sertac Sayin Dr. Ali Akansu, Thesis Advisor Date Professor of Electrical and Computer Engineering, NJIT Dr. Alex Haimovich, Committee Member Date Professor of Electrical and Computer Engineering, NJIT Dr. Osvaldo Simeone, Committee Member Date Assistant Professor of Electrical and Computer Engineering, NJIT BIOGRAPHICAL SKETCH Author: Sertac Sayin Degree: Master of Science Date: May 2010 Undergraduate and Graduate Education: • Master of Science in Electrical Engineering, New Jersey Institute of Technology, Newark, NJ, 2010 • Bachelor of Science in Electrical Engineering, Middle East Technical University, Ankara, Turkey, 2003 Major: Electrical Engineering Svl nn Sbt S vl bb Sn Sn ye vl bl En Sn blvd thr Sbt Sn blvd fthr Sn S nd blvd tr En Sn ACKOWEGME First of all, I would like to express my sincere gratitude to my advisor, Professor Ali, Akansu, for all his support, encouragement and his guidance throughout my Master's study. He prepared me for the professional life. I am very grateful to Professor Alexander Haimovich and Assistant Professor Osvaldo Simeon of the ECE Department of NJIT for aggreing to participate on my thesis committee. I would like to thank to the Scientific and Technological Research Council of Turkey (TUBITAK) for their financial support for my master's study. I am proud they chose me out of many candidates. The last and the most, I would like to thank my family for their support. Even though they are 5000 miles away, they were always there for me. Especially, I want to thank them for the long, supportive and encouraging phone calls. Without them I could not finish this thesis. v TABLE OF CONTENTS Chapter Page 1 INTRODUCTION 1 1.1 Objective 1 1.2 Background Information 1 2 LTE OVERVIEW AS OFDMA AND SCFDMA 3 2.1 OFDMA 3 2.2 OFDMA Architecture 5 2.3 OFDMA Frame Structure 6 2.4 SCFDMA 6 2.5 SCFDMA Architecture 7 2.6 SCFDMA Frame Structure 12 3 GENERALIZED DFT 14 3.1 Theory of DFT and GDFT 14 3.2 GDFT Design 16 4 PEAK TO AVERAGE POWER RATIO REDUCTION IN SCFDMA WITH GDFT 18 4.1 Theory 18 4.2 SCFDMA Analysis 19 4.3 Design and Performance of GDFT Based SCFDMA 21 5 CONCLUSION 34 APPENDIX MATLAB CODE USED FOR SIMULATIONS 36 REFERENCES 40 vii LIST OF FIGURES Figure Page 2.1 Conventional FDMA (the upper one) and Orthogonal (the lower one) FDMA 3 2.2 The carrier signals in frequency domain and in time domain 4 2.3 OFDMA system block diagram 6 2.4 Difference Between Channel Representations Between OFDMA and SCFDMA... 7 2.5 SCFDMA system block diagram for transmitter and receiver 8 2.6 SCFDMA Subcarrier Mappings; Distributed and Localized Modes 9 2.7 Comparison of PAPR for different subcarrier mapping types of SCFDMA with DFT size 16 and IDFT size 512 10 2.8 Comparison of CCDF of PAPR for IFDMA, DFDMA, LFDMA and OFDMA..... 11 2.9 Resource block for LTE system 13 4.1 SCFDMA block diagram 19 4.2 Position of elements of° (a) before multiplying (b) after multiplying with G matrix 24 4.3 Position of elements of 0 (a) before multiplying (b) after multiplying with G matrix 26 4.4 Proposed SCFDMA system block diagram 27 4.5 CCDF of PAPR for SCFDMA with DFT or GDFT size (N) =16 and IDFT size=32 with BPSK digital modulation 28 4.6 CCDF of PAPR for SCFDMA with DFT or GDFT size (N) =16 and IDFT size=64 with BPSK digital modulation 28 4.7 CCDF of PAPR for SCFDMA with DFT or GDFT size (N) =16 and IDFT size=512 with BPSK digital modulation 29 4.8 CCDF of PAPR for SCFDMA with DFT or GDFT size (N) =16 and IDFT size=2048 with BPSK digital modulation 29 viii LIST OF FIGURES (Continued) Figure Page 4.9 CCDF of PAPR for SCFDMA with DFT or GDFT size (N) =32 and IDFT size=64 with BPSK digital modulation 30 4.10 CCDF of PAPR for DFT or GDFT size (N) =16 and IDFT size=128, SCFDMA with BPSK digital modulation 30 4.11 CCDF of PAPR for DFT or GDFT size (N) =16 and IDFT-size=128, SCFDMA with BPSK digital modulation 31 4.12 CCDF of PAPR for DFT or GDFT size (N) =8 and IDFT size=16, SCFDMA with QPSK digital modulation 31 4.13 CCDF of PAPR for DFT or GDFT size (N) =64 and IDFT size=128, SCFDMA with QPSK digital modulation 32 4.14 CCDF of PAPR for DFT or GDFT size (N) =32 and IDFT size=64, SCFDMA with QAM digital modulation 32 ix CHAPTER 1 INTRODUCTION 1.1 Objective Objective of this thesis is to introduce a method to reduce peak to average power (PAPR) for Single Carrier Frequency Division Multiple Access (SCFDMA) with the Localized Frequency Division Multiple Access (LFDMA) subcarrier mapping for different digital modulation types like; Binary Phase Shift Keying (BPSK), Quadrature Phase Shift Keying (QPSK) and 16 Quadrature Amplitude Modulation (QAM). As background information, Long Term Evolution (LTE), a beyond third generation mobile broadband standard, successor to UMTS and CDMA2000 (which are 3G cellular technologies), is reviewed as two parts downlink, Orthogonal Frequency Division Multiple Access (OFDMA) and uplink SCFDMA. And Generalized Discrete Fourier Transform (GDFT) is introduced. Finally, the difference between conventional SCFDMA system and the proposed SCFDMA system is compared in terms of PAPR with different sizes of frequency band and different number of users. 1.2 Background Information Since the beginning of humanity, communication is one of the basic needs. At first, they started to communicate through fire, smoke... etc and then, the telegraph was invented. Wired phone invention followed telegraph and today, with the technological improvements, people can communicate wirelessly between each other through cell 1 2 phones in their pockets. Engineers are always looking for faster, reliable and safer solutions to problems. In the wireless communication field, the technology that is used as 3 rd Generation (3G) in the cell phones which is Code division Multiple Access (CDMA) based, has achieved its limits. So for further increase in throughput, the technology is changed to LTE. And LTE is based on OFDM in the downlink channel (link from station to mobile) and Discrete Fourier Transform (DFT) spread OFDM or in other words SCFDMA in the uplink channel (link from mobile to station). The reason to use two different standards for uplink and downlink is PAPR. PAPR is directly related to battery life of the mobile. So PAPR is not a big issue for downlink because station is stationary and does not require battery. However, mobiles are using battery therefore battery life is one of the biggest issues for them. SCFDMA has similar throughput performance and essentially the same overall complexity as OFDMA. A principal advantage of SC-FDMA is the peak-to-average power ratio (PAPR), which is lower than that of OFDMA. SCFDMA is currently a strong candidate for the uplink multiple access scheme in the Long Term Evolution of cellular systems under consideration by the Third Generation Partnership Project (3GPP).
Load more

Recommended publications
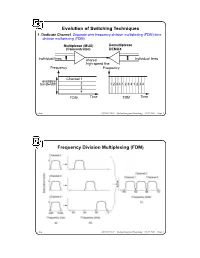
  • Evolution of Switching Techniques Frequency Division Multiplexing
    Evolution of Switching Techniques 1. Dedicate Channel. Separate wire frequency division multiplexing (FDM) time division multiplexing (TDM) Multiplexor (MUX) Demultiplexor (Concentrator) DEMUX individual lines shared individual lines high speed line Frequency Frequency Channel 1 available bandwidth 2 1 2 3 4 1 2 3 4 1 2 3 4 3 4 FDM Time TDM Time chow CS522 F2001—Multiplexing and Switching—10/17/2001—Page 1 Frequency Division Multiplexing (FDM) chow CS522 F2001—Multiplexing and Switching—10/17/2001—Page 2 Wavelength Division Multiplexing chow CS522 F2001—Multiplexing and Switching—10/17/2001—Page 3 Impact of WDM z Many big organizations are starting projects to design WDM system or DWDN (Dense Wave Division Mutiplexing Network). We may see products appear in next three years.In Fujitsu and CCL/Taiwan, 128 different wavelengthes on the same strand of fiber was reported working in the lab. z We may have optical routers between end systems that can take one wavelenght signal, covert to different wavelenght, send it out on different links. Some are designing traditional routers that covert optical signal to electronical signal, and use time slot interchange based on high speed memory to do the switching, the convert the electronic signal back to optical signal. z With this type of optical networks, we will have a virtual circuit network, where each connection is assigned some wave length. Each connection can have 2.4 gbps tremedous bandwidth. z With inital 128 different wavelength, we can have about 10 end users. If each pair of end users needs to communicate simultaneously, it will use 10*10=100 different wavelength.
    [Show full text]
  • Lecture 8: Overview of Computer Networking Roadmap
    Lecture 8: Overview of Computer Networking Slides adapted from those of Computer Networking: A Top Down Approach, 5th edition. Jim Kurose, Keith Ross, Addison-Wesley, April 2009. Roadmap ! what’s the Internet? ! network edge: hosts, access net ! network core: packet/circuit switching, Internet structure ! performance: loss, delay, throughput ! media distribution: UDP, TCP/IP 1 What’s the Internet: “nuts and bolts” view PC ! millions of connected Mobile network computing devices: server Global ISP hosts = end systems wireless laptop " running network apps cellular handheld Home network ! communication links Regional ISP " fiber, copper, radio, satellite access " points transmission rate = bandwidth Institutional network wired links ! routers: forward packets (chunks of router data) What’s the Internet: “nuts and bolts” view ! protocols control sending, receiving Mobile network of msgs Global ISP " e.g., TCP, IP, HTTP, Skype, Ethernet ! Internet: “network of networks” Home network " loosely hierarchical Regional ISP " public Internet versus private intranet Institutional network ! Internet standards " RFC: Request for comments " IETF: Internet Engineering Task Force 2 A closer look at network structure: ! network edge: applications and hosts ! access networks, physical media: wired, wireless communication links ! network core: " interconnected routers " network of networks The network edge: ! end systems (hosts): " run application programs " e.g. Web, email " at “edge of network” peer-peer ! client/server model " client host requests, receives
    [Show full text]
  • Circuit-Switched Coherence
    Circuit-Switched Coherence ‡Natalie Enright Jerger, ‡Mikko Lipasti, and ?Li-Shiuan Peh ‡Electrical and Computer Engineering Department, University of Wisconsin-Madison ?Department of Electrical Engineering, Princeton University Abstract—Circuit-switched networks can significantly lower contention, overall system performance can degrade by 20% the communication latency between processor cores, when or more. This latency sensitivity coupled with low link uti- compared to packet-switched networks, since once circuits are set up, communication latency approaches pure intercon- lization motivates our exploration of circuit-switched fabrics nect delay. However, if circuits are not frequently reused, the for CMPs. long set up time and poorer interconnect utilization can hurt Our investigations show that traditional circuit-switched overall performance. To combat this problem, we propose a hybrid router design which intermingles packet-switched networks do not perform well, as circuits are not reused suf- flits with circuit-switched flits. Additionally, we co-design a ficiently to amortize circuit setup delay. This observation prediction-based coherence protocol that leverages the exis- motivates a network with a hybrid router design that sup- tence of circuits to optimize pair-wise sharing between cores. The protocol allows pair-wise sharers to communicate di- ports both circuit and packet switching with very fast circuit rectly with each other via circuits and drives up circuit reuse. reconfiguration (setup/teardown). Our preliminary results Circuit-switched coherence provides overall system perfor- show this leading to up to 8% improvement in overall system mance improvements of up to 17% with an average improve- performance over a packet-switched fabric. ment of 10% and reduces network latency by up to 30%.
    [Show full text]
  • Medium Access Control Layer
    Telematics Chapter 5: Medium Access Control Sublayer User Server watching with video Beispielbildvideo clip clips Application Layer Application Layer Presentation Layer Presentation Layer Session Layer Session Layer Transport Layer Transport Layer Network Layer Network Layer Network Layer Univ.-Prof. Dr.-Ing. Jochen H. Schiller Data Link Layer Data Link Layer Data Link Layer Computer Systems and Telematics (CST) Physical Layer Physical Layer Physical Layer Institute of Computer Science Freie Universität Berlin http://cst.mi.fu-berlin.de Contents ● Design Issues ● Metropolitan Area Networks ● Network Topologies (MAN) ● The Channel Allocation Problem ● Wide Area Networks (WAN) ● Multiple Access Protocols ● Frame Relay (historical) ● Ethernet ● ATM ● IEEE 802.2 – Logical Link Control ● SDH ● Token Bus (historical) ● Network Infrastructure ● Token Ring (historical) ● Virtual LANs ● Fiber Distributed Data Interface ● Structured Cabling Univ.-Prof. Dr.-Ing. Jochen H. Schiller ▪ cst.mi.fu-berlin.de ▪ Telematics ▪ Chapter 5: Medium Access Control Sublayer 5.2 Design Issues Univ.-Prof. Dr.-Ing. Jochen H. Schiller ▪ cst.mi.fu-berlin.de ▪ Telematics ▪ Chapter 5: Medium Access Control Sublayer 5.3 Design Issues ● Two kinds of connections in networks ● Point-to-point connections OSI Reference Model ● Broadcast (Multi-access channel, Application Layer Random access channel) Presentation Layer ● In a network with broadcast Session Layer connections ● Who gets the channel? Transport Layer Network Layer ● Protocols used to determine who gets next access to the channel Data Link Layer ● Medium Access Control (MAC) sublayer Physical Layer Univ.-Prof. Dr.-Ing. Jochen H. Schiller ▪ cst.mi.fu-berlin.de ▪ Telematics ▪ Chapter 5: Medium Access Control Sublayer 5.4 Network Types for the Local Range ● LLC layer: uniform interface and same frame format to upper layers ● MAC layer: defines medium access ..
    [Show full text]
  • F. Circuit Switching
    CSE 3461: Introduction to Computer Networking and Internet Technologies Circuit Switching Presentation F Study: 10.1, 10.2, 8 .1, 8.2 (without SONET/SDH), 8.4 10-02-2012 A Closer Look At Network Structure: • network edge: applications and hosts • network core: —routers —network of networks • access networks, physical media: communication links d. xuan 2 1 The Network Core • mesh of interconnected routers • the fundamental question: how is data transferred through net? —circuit switching: dedicated circuit per call: telephone net —packet-switching: data sent thru net in discrete “chunks” d. xuan 3 Network Layer Functions • transport packet from sending to receiving hosts application transport • network layer protocols in network data link network physical every host, router network data link network data link physical data link three important functions: physical physical network data link • path determination: route physical network data link taken by packets from source physical to dest. Routing algorithms network network data link • switching: move packets from data link physical physical router’s input to appropriate network data link application router output physical transport network data link • call setup: some network physical architectures require router call setup along path before data flows d. xuan 4 2 Network Core: Circuit Switching End-end resources reserved for “call” • link bandwidth, switch capacity • dedicated resources: no sharing • circuit-like (guaranteed) performance • call setup required d. xuan 5 Circuit Switching • Dedicated communication path between two stations • Three phases — Establish (set up connection) — Data Transfer — Disconnect • Must have switching capacity and channel capacity to establish connection • Must have intelligence to work out routing • Inefficient — Channel capacity dedicated for duration of connection — If no data, capacity wasted • Set up (connection) takes time • Once connected, transfer is transparent • Developed for voice traffic (phone) g.
    [Show full text]
  • Application Note: 2-Cell Test Environment
    Application Note 2-cell Test Environment MD8475A Signalling Tester 1. Background to LTE Rollout Mobile phones appearing in the late 1980s soon experienced rapid evolution of functions from 1990 to 2000 and also spread worldwide as key communications infrastructure. The mobile phone is not limited to just two-way communications between two people but also supports sending and receiving of Short Message Services (SMS), web browsing using the Internet, application and video download, etc., and has become a popular and key cultural tool supporting a fuller lifestyle for many people. Figure 1. Evolution on UE According to one research company, total mobile phone (terminal) shipments at the end of 2010 were valued at $38 billion split between 45% for 2G phones and 49% for 3G. Table 1. Mobile Terminal Shipments Mobile Terminal Shipments ($38 billion total) LTE 1.3% WiMAX 4.0% W-CDMA 40.0% CDMA 9.3% GSM 45.4% 1 MD8475A-E-F-1 The purpose of the shift from 2G to 3G systems was to make more efficient use of frequency bandwidths and was closely related to the explosive growth of the Internet. While still maintaining the easy portability of a mobile phone, users were able to access the information they needed easily at any time and place using the Internet. Similarly to growth of 3G technology, the requirements of LTE systems, which is are positioned in the market as 3.9G to maintain competitiveness with coming 4G systems, are being examined. Connectivity with IP-based core networks must be maintained to support multimedia applications and ubiquitous networks using the packet domain.
    [Show full text]
  • Research on Super 3G Technology
    03-10E_T-Box_3.3 06.12.26 10:07 AM ページ 55 NTT DoCoMo Technical Journal Vol. 8 No.3 Part 2: Research on Super 3G Technology In this part 2 of the Super 3G research that is being conducted to achieve a smooth transition from 3G to 4G, we present technology that is currently being studied for standardization as technical details. Sadayuki Abeta, Minami Ishii, Yasuhiro Kato and Kenichi Higuchi At the RAN WG1 meeting of November 2005, there was 1. Introduction agreement by many companies that high commonality is As explained in part1, Super 3G, the so-called Evolved extremely important and wireless access should be the same for URAN and UTRAN or Long term evolution by the 3rd FDD (paired spectrum) and TDD (unpaired spectrum). As this Generation Partnership Project (3GPP) has been extensively common wireless access system for FDD and TDD, Orthogonal studied since 2005. Agreement on the requirement was reached Frequency Division Multiple Access (OFDMA), which features in June of 2005 to begin investigation of specific technologies. highly efficient frequency utilization was approved for the In June 2006, it was agreed that investigation of the feasibility downlink and Single-Carrier Frequency Division Multiple of the basic approach for satisfying the requirements was essen- Access (SC-FDMA) was approved for the uplink at the tially completed, and effort shifted to the work item phase to December 2005 Plenary Meeting. start the detailed specifications work. Here, we explain technol- The features of the wireless access system are described in ogy that has been proposed as study items.
    [Show full text]
  • UMTS Core Network
    UMTS Core Network V. Mancuso, I. Tinnirello GSM/GPRS Network Architecture Radio access network GSM/GPRS core network BSS PSTN, ISDN PSTN, MSC GMSC BTS VLR MS BSC HLR PCU AuC SGSN EIR BTS IP Backbone GGSN database Internet V. Mancuso, I. Tinnirello 3GPP Rel.’99 Network Architecture Radio access network Core network (GSM/GPRS-based) UTRAN PSTN Iub RNC MSC GMSC Iu CS BS VLR UE HLR Uu Iur AuC Iub RNC SGSN Iu PS EIR BS Gn IP Backbone GGSN database Internet V. Mancuso, I. Tinnirello 3GPP RelRel.’99.’99 Network Architecture Radio access network 2G => 3G MS => UE UTRAN (User Equipment), often also called (user) terminal Iub RNC New air (radio) interface BS based on WCDMA access UE technology Uu Iur New RAN architecture Iub RNC (Iur interface is available for BS soft handover, BSC => RNC) V. Mancuso, I. Tinnirello 3GPP Rel.’99 Network Architecture Changes in the core Core network (GSM/GPRS-based) network: PSTN MSC is upgraded to 3G MSC GMSC Iu CS MSC VLR SGSN is upgraded to 3G HLR SGSN AuC SGSN GMSC and GGSN remain Iu PS EIR the same Gn GGSN AuC is upgraded (more IP Backbone security features in 3G) Internet V. Mancuso, I. Tinnirello 3GPP Rel.4 Network Architecture UTRAN Circuit Switched (CS) core network (UMTS Terrestrial Radio Access Network) MSC GMSC Server Server SGW SGW PSTN MGW MGW New option in Rel.4: GERAN (GSM and EDGE Radio Access Network) PS core as in Rel.’99 V. Mancuso, I. Tinnirello 3GPP Rel.4 Network Architecture MSC Server takes care Circuit Switched (CS) core of call control signalling network The user connections MSC GMSC are set up via MGW Server Server (Media GateWay) SGW SGW PSTN “Lower layer” protocol conversion in SGW MGW MGW (Signalling GateWay) RANAP / ISUP PS core as in Rel.’99 SS7 MTP IP Sigtran V.
    [Show full text]
  • Circuit Switching in the Internet
    CIRCUIT SWITCHING IN THE INTERNET A DISSERTATION SUBMITTED TO THE DEPARTMENT OF ELECTRICAL ENGINEERING AND THE COMMITTEE ON GRADUATE STUDIES OF STANFORD UNIVERSITY IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY Pablo Molinero Fernandez June 2003 Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. UMI Number: 3090644 Copyright 2003 by Molinero Fernandez, Pablo All rights reserved. ® UMI UMI Microform 3090644 Copyright 2003 by ProQuest Information and Learning Company. All rights reserved. This microform edition is protected against unauthorized copying under Title 17, United States Code. ProQuest Information and Learning Company 300 North Zeeb Road P.O. Box 1346 Ann Arbor, Ml 48106-1346 Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. © Copyright by Pablo Molinero Fernandez 2003 All Rights Reserved ii Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. I certify that I have read this dissertation and that, in my opinion, it is fully adequate in scope and quality as a dissertation for the degree ofD/pctor of Philosophy. Nick McKeown (Principal Adviser) I certify that I have read this dissertation and that, in my opinion, it is fully adequate in scope and quality as a dissertation for the degree of Doctor of Philosophy. _______________ Balaji Prabhakar I certify that I have read this dissertation and that, in my opinion, it is fully adequate in scope and quality as a dissertation for the degree of Doctor of Philosophy. NfSibTas Bambos Approved for the University Committee on Graduate Studies: iii Reproduced with permission of the copyright owner.
    [Show full text]
  • Chapter 10: Circuit Switching and Packet Switching Switching Networks
    Chapter 10: Circuit Switching and Packet Switching CS420/520 Axel Krings Page 1 Sequence 10 Switching Networks • Long distance transmission is typically done over a network of switched nodes • Nodes not concerned with content of data • End devices are stations — Computer, terminal, phone, etc. • A collection of nodes and connections is a communications network • Data is routed by being switched from node to node CS420/520 Axel Krings Page 2 Sequence 10 1 Nodes • Nodes may connect to other nodes only, or to stations and other nodes • Node to node links usually multiplexed • Network is usually partially connected — Some redundant connections are desirable for reliability • Two different switching technologies — Circuit switching — Packet switching CS420/520 Axel Krings Page 3 Sequence 10 Simple Switched Network CS420/520 Axel Krings Page 4 Sequence 10 2 Circuit Switching • Dedicated communication path between two stations • Three phases — Establish — Transfer — Disconnect • Must have switching capacity and channel capacity to establish connection • Must have intelligence to work out routing CS420/520 Axel Krings Page 5 Sequence 10 Circuit Switching • Inefficient — Channel capacity dedicated for duration of connection — If no data, capacity wasted • Set up (connection) takes time • Once connected, transfer is transparent • Developed for voice traffic (phone) CS420/520 Axel Krings Page 6 Sequence 10 3 Public Circuit Switched Network CS420/520 Axel Krings Page 7 Sequence 10 Telecom Components • Subscriber — Devices attached to network • Subscriber
    [Show full text]
  • Offset Time-Emulated Architecture for Optical Burst Switching - Modelling and Performance Evaluation Autor De La Tesi: Mirosław Klinkowski
    Universitat Politecnica` de Catalunya Departament d'Arquitectura de Computadors O®set Time-Emulated Architecture for Optical Burst Switching - Modelling and Performance Evaluation Ph.D. thesis by MirosÃlaw Klinkowski Advisor: Dr. Davide Careglio Co-advisors: Prof. Josep Sol¶ei Pareta, and Prof. Marian Marciniak PhD Program: Arquitectura i Tecnologia de Computadors November 2007 ACTA DE QUALIFICACIÓ DE LA TESI DOCTORAL Reunit el tribunal integrat pels sota signants per jutjar la tesi doctoral: Títol de la tesi: Offset Time-Emulated Architecture for Optical Burst Switching - Modelling and Performance Evaluation Autor de la tesi: Mirosław Klinkowski Acorda atorgar la qualificació de: No apte Aprovat Notable Excel·lent Excel·lent Cum Laude Barcelona, …………… de/d’….................…………….. de ..........…. El President El Secretari ............................................. ............................................ (nom i cognoms) (nom i cognoms) El vocal El vocal El vocal ............................................. ............................................ ..................................... (nom i cognoms) (nom i cognoms) (nom i cognoms) To Ola and my parents Acknowledgments to Marian, Josep, Davide, and MichaÃl for their measureless support, inspiration and for guiding me through the research of this thesis Wala, Barbara, Andrzej and MichaÃl for encouraging me at the very beginning of this thesis And to my family for their love, support, and for being always with me Contents List of Figures v List of Tables ix Summary xi Resum xv Structure of the thesis xix 1 Introduction 1 1.1 Optical Transport Networks . 2 1.2 Overview of the Thesis . 4 PART I: Background 7 2 Optical switching architectures 9 2.1 Principle of operation . 10 2.1.1 Optical circuit switching (OCS) . 10 2.1.2 Optical packet switching (OPS) . 10 2.1.3 Optical burst switching (OBS) .
    [Show full text]
  • 6.02 Spring 2011 Lecture #18 Next Steps… Multi-Hop Networks
    Next Steps… • Have: digital point-to-point We’ve worked on link signaling, reliability, sharing • Want: many interconnected points 6.02 Spring 2011 Lecture #18 Your Network • multi-hop networks: design criteria Here! • network topologies • circuit vs. packet switching • queues, Little’s Law 6.02 Spring 2011 Lecture 18, Slide #1 6.02 Spring 2011 Lecture 18, Slide #2 Multi-hop Networks Network Reliability • Design engineers: Link – Low MTBF components, failure prediction – Easy to identify and fix problems • Remote observability and controllability End point – Replace/expand/evolve network incrementally Switch – Defend against malicious users • Redundancy – No single point of failure – Fail-safe, Fail-safe, Fail-hard • Switches orchestrate flow of information through the network, – Automated adaptation to component failures often multiplexing many logically-independent flows over a single physical link. • Degradation, not failure – Appropriate sharing of network resources • Users: – Circuit switching vs. packet switching – High availability • Design criteria – Meaningful feedback on failure (e.g., busy signal) – Reliability, scalability, performance, cost, security, … 6.02 Spring 2011 Lecture 18, Slide #3 6.02 Spring 2011 Lecture 18, Slide #4 Network Scalability Network Performance • Enable incremental build-out • Design Engineers – increase in usage involves incremental costs (both at edges and – Utilization in interior of network) – Minimize protocol overhead – Address bottlenecks without fundamental changes – Quality of Service (performance
    [Show full text]