Convergent Evolution of Boats with Sails A
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Steering and Stabilisation Set a Course for Optimum Reliability and Performance
Marine Steering and stabilisation Set a course for optimum reliability and performance 1 Systems that keep vessels safely on course and comfortable in all conditions Since pioneering electro-hydraulic steering gear nearly a century ago, we continue to develop new systems for vessels ranging from large tankers to super yachts. Customers benefit from the world leading hydrodynamics expertise and the design resources of the Rolls-Royce rudder, steering gear, stabilisation and propulsion specialists, who cooperate to address and handle challenging projects and deliver system solutions. This minimises technical risk as well as maximising vessel performance. move Contents: Steering gear page 4 Promas page 10 Rudders page 12 Stabilisers page 18 Customer support page 22 movemake the right Steering gear Rotary vane steering gear for smaller vessels The SR series is designed with integrated frequency controlled pumps. General description Rolls-Royce supplies a complete range of steering gear, suitable for selection, alarm panels and rudder angle indicators or just a portion all types and sizes of ships. The products are designed as complete of this. The system is also prepared for interface to VDR, ships main steering systems with the actuator, power pack, steering control, alarm system, autopilot, joystick and DP when requested. Due to a alarm and rudder angle indicating system in mind, and can wide range of demands, great care has been taken from material therefore be delivered with complete control systems, including selection through construction, -

2013 Owner's Manual
O W NER ’ S M A N U A L WELCOME TO DAGGER EUROPE BE PART OF THE COMMUNITY You are in good company. Over the years Dagger From the mountains to the sea, Dagger paddlers has crafted a reputation for being at the cutting are relentless in the pursuit of adventure and play. edge of paddlesport, which is why so many of the Join in at www.daggereurope.com to share your worlds most passionate and well-known paddlers experiences, see what the team have been doing choose to use our boats. Like them, you’ll find and get the latest news. your Dagger kayak will provide years of adventure wherever you want to go, and maybe places you CONTENTS haven’t thought of yet. 4 Kayak Key Features: Recreational/Touring 5 Kayak Key Features: Whitewater Formed in the late 80’s, Dagger has spent over two decades innovating and developing to create 6 Outfitting classic designs that always deliver performance, 12 Storage & Transport comfort and value. This guide will help you get 13 Care & Maintenance the best from your new Dagger kayak and also Additional Equipment ensure it stays in good condition throughout your 14 paddling adventures. 15 Your Safety 16 Warranty Thank you for choosing Dagger kayaks. 17 Service & Support This owner’s manual and additional information is available at www.daggereurope.com KAYAK KEY FEATURES: RECREATIONAL / TOURING Rudder (some models) Stern Seat & seatback Large hatch Backband adjuster Security bar Cockpit Thighbraces Deck Deck rigging Small hatch Grab handle Compass Bow Skeg Rail (some models) Sidewall Skeg/rudder lanyard Hull Foot brace bolts Deck lines, bow and stern Chine FEATURES IN DETAIL BOW/NOSE: The front of the kayak. -

(12) Patent Application Publication (10) Pub. No.: US 2011/0053441 A1 Sakamoto (43) Pub
US 2011 0053441A1 (19) United States (12) Patent Application Publication (10) Pub. No.: US 2011/0053441 A1 Sakamoto (43) Pub. Date: Mar. 3, 2011 (54) TWIN-SKEGSHIP (52) U.S. Cl. .......................................................... 440/66 (76) Inventor: Toshinobu Sakamoto, Nagasaki (JP) (21) Appl. No.: 12/990,009 (57) ABSTRACT Provided is a twin-skeg ship that allows for a further improve (22) PCT Filed: Oct. 20, 2008 ment in propulsion performance (propulsion efficiency). A twin-skeg ship (10) having a pair of left and right skegs (3) on (86). PCT No.: PCT/UP2008/068987 the bottom (2) of a stern has reaction fins 5, each comprising a plurality of fins 5a extending radially from a bossing (6) S371 (c)(1), fixed to a stern frame (7) provided at a rear end of the skeg (3), (2), (4) Date: Nov. 12, 2010 or from a fin boss provided on the bossing (6), in a range O O where a flow immediately in front of a propeller (4) attached Publication Classification to the skeg (3) with a propeller shaft (4a) therebetween has a (51) Int. Cl. component in the same direction as a rotational direction of B63H I/28 (2006.01) the propeller (4). SKEG HULL SKEG CENTERLINE CENTERLINE CENTERLINE Patent Application Publication Mar. 3, 2011 Sheet 1 of 8 US 2011/0053441 A1 - O s as e rs CO - d - CD s to v ? ? CY se Patent Application Publication Mar. 3, 2011 Sheet 2 of 8 US 2011/0053441 A1 N LL 2. C9 d - Salt CMO H. 2 CD CN 2 -- CD E----- a caaaad m H t Lal CP : : Patent Application Publication Mar. -

Make Handy Boat Your Home Port in 2012 Fuel, Ice, Supplies Stop by Our New Marine Facilities Gasoline & Diesel to Discuss Your Boating Needs
Maine Yacht Racing 2012 The offiicall Yearbook of the Guullf of Maiine Ocean Raciing Associiatiion www.gmora.org !!"## $ %& '( ' )!' )%$ HANDY BOAT SERVICE A Full Service Boatyard Boat Storage Painting & Gelcoat Yacht Rigging Fiberglass Repair Re-Powering Launch Service Moorings Make Handy Boat your home port in 2012 Fuel, Ice, Supplies Stop by our new marine facilities Gasoline & Diesel to discuss your boating needs. Mechanical Repairs Join us at the new Falmouth Sea Grill. Custom Wood Work 215 Foreside Rd. Falmouth, ME 04105 (207) 781-5110 www.handyboat.com 2 www.gmora.org Maine Yacht Racing She’s Taken You To Bermuda, The Caribbean And The Bras d’Or Lakes. Perhaps It’s Time You Took Her To Morris. MorrisCare. The Refit, Refined. Let MorrisCare take your expectations for ser vice some of the world’s most admired yachts. to a completely new level. At Morris there is no job On top of that, our yards in Northeast Harbor and we haven’t seen before and no special fabrication Bass Harbor are situated in the heart of Maine’s most beyond our capabilities. Whether we troubleshoot dramatic cruising grounds. Penobscot Bay, Blue Hill Bay, a small electrical problem and send you on your offshore islands and Acadia National Park are all right way or undertake a major refit, you’ll quickly at our doorstep. A rewarding destination unto itself. see the difference Morris service Don’t you think your boat deserves a people make. trip to Morris? Maybe you should come to That means you can plan to repaint, our doorstep as well. -

2021 Transpacific Yacht Race Event Program
TRANSPACTHE FIFTY-FIRST RACE FROM LOS ANGELES 2021 TO HONOLULU 2 0 21 JULY 13-30, 2021 Comanche: © Sharon Green / Ultimate Sailing COMANCHE Taxi Dancer: © Ronnie Simpson / Ultimate Sailing • Hamachi: © Team Hamachi HAMACHI 2019 FIRST TO FINISH Official race guide - $5.00 2019 OVERALL CORRECTED TIME WINNER P: 808.845.6465 [email protected] F: 808.841.6610 OFFICIAL HANDBOOK OF THE 51ST TRANSPACIFIC YACHT RACE The Transpac 2021 Official Race Handbook is published for the Honolulu Committee of the Transpacific Yacht Club by Roth Communications, 2040 Alewa Drive, Honolulu, HI 96817 USA (808) 595-4124 [email protected] Publisher .............................................Michael J. Roth Roth Communications Editor .............................................. Ray Pendleton, Kim Ickler Contributing Writers .................... Dobbs Davis, Stan Honey, Ray Pendleton Contributing Photographers ...... Sharon Green/ultimatesailingcom, Ronnie Simpson/ultimatesailing.com, Todd Rasmussen, Betsy Crowfoot Senescu/ultimatesailing.com, Walter Cooper/ ultimatesailing.com, Lauren Easley - Leialoha Creative, Joyce Riley, Geri Conser, Emma Deardorff, Rachel Rosales, Phil Uhl, David Livingston, Pam Davis, Brian Farr Designer ........................................ Leslie Johnson Design On the Cover: CONTENTS Taxi Dancer R/P 70 Yabsley/Compton 2019 1st Div. 2 Sleds ET: 8:06:43:22 CT: 08:23:09:26 Schedule of Events . 3 Photo: Ronnie Simpson / ultimatesailing.com Welcome from the Governor of Hawaii . 8 Inset left: Welcome from the Mayor of Honolulu . 9 Comanche Verdier/VPLP 100 Jim Cooney & Samantha Grant Welcome from the Mayor of Long Beach . 9 2019 Barndoor Winner - First to Finish Overall: ET: 5:11:14:05 Welcome from the Transpacific Yacht Club Commodore . 10 Photo: Sharon Green / ultimatesailingcom Welcome from the Honolulu Committee Chair . 10 Inset right: Welcome from the Sponsoring Yacht Clubs . -
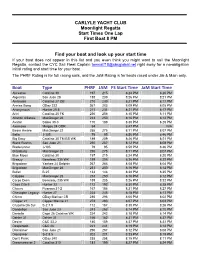
Boat Type PHRF JAM FS Start Time Jam Start Time
CARLYLE YACHT CLUB Moonlight Regatta Start Times One Lap First Boat 8 PM Find your boat and look up your start time If your boat does not appear in this list and you even think you might want to sail the Moonlight Regatta, contact the CYC Sail Fleet Captain [email protected] right away for a no-obligation initial rating and start time for your boat. The PHRF Rating is for full racing sails, and the JaM Rating is for boats raced under Jib & Main only. Boat Type PHRF JAM FS Start Time JaM Start Time Akcestas Catalina 30 197 215 8:24 PM 8:20 PM Algeciras San Juan 28 188 209 8:26 PM 8:21 PM Ambrosia Catalina 27 OB 210 230 8:21 PM 8:17 PM Annies Song ODay 222 267 283 8:09 PM 8:05 PM Anonymous Hunter 25.5 211 231 8:21 PM 8:17 PM Ariel Catalina 25 FK 236 256 8:15 PM 8:11 PM Atlantic Alliance MacGregor 26 233 250 8:16 PM 8:12 PM Avatar Sabre 30-3 170 189 8:30 PM 8:26 PM Axomoxa Melges 24 ODR 94 8:47 PM N/A Beare Amare MacGregor 22 255 275 8:11 PM 8:07 PM Bella J-105 79 95 8:50 PM 8:46 PM Big Easy Catalina 30 TM BS WK 189 209 8:26 PM 8:21 PM Black Rushin San Juan 21 250 267 8:12 PM 8:08 PM Bladerunner J-105 79 95 8:50 PM 8:46 PM Blitzeburg MacGregor 22 255 275 8:11 PM 8:07 PM Blue Moon Catalina 30 197 215 8:24 PM 8:20 PM Breezy Beneteau 235 WK 189 205 8:26 PM 8:22 PM Brigadoon Yankee 24 Dolphin 267 286 8:08 PM 8:04 PM Brigadoon MacGregor 26 233 250 8:16 PM 8:12 PM Bullet B-25 133 148 8:38 PM 8:35 PM Calypso MacGregor 26 233 250 8:16 PM 8:12 PM Carpe Diem Beneteau 235 WK 189 205 8:26 PM 8:22 PM Casa Cita II Hunter 33 172 192 8:30 PM 8:25 -

Binnen-Yardstick Tiefwasser 2008
Österreichischer Segel-Verband Binnen-Yardstick Tiefwasser 2008 Die Zusatzbuchstaben nach der Bootstype bedeutet: HBK Hubkiel KMK Kimmkiel KLS Kielschwerter KUK Kurzkiel MTK Mittelkiel SCH Schwert SWK Schwenkkiel 11 metre One Design 86 14-Foot-Dinghi 93 18-Foot-Skiff 74 29er 100 49er 78 808er 100 8m One Design HBK 7/8 Spi 91 8m One Design HBK Topspi 89 A A-Cat 76 AS 21 -> K21 Achat-Jolle 121 Achilles 24 110 Akros (12m Mast) 90 Akros (bis 13m) 84 Akros (bis 14m) 83 Akros (gr. 14m) 82 Albin Express 102 Albin Viggen 115 Alp Sail Putiferio V 97 Alpa 22 117 Alpa 515 113 Alpa 550 124 Anderson 22 120 Aquila Kiel 113 Aquila Schwert 110 Argo 680 N 99 Asso 99 (Standard) 83 Assunta (Krainer) 96 Atalanta 616 110 B BB 11 122 BB 17 119 Balaton 21 MTK 112 Balaton 24 MTK 112 Balaton 25 MTK 113 Ballad 107 Bandholm 24 117 Banner 1/2 tonner 99 Banner 23 Racer MTK 93 Banner 28 Racer 100 Bavaria 29 Speed N 101 Bavaria 30/300 111 Bavaria 32 106 Bavaria 34 96 Bavaria 606 MTK 116 Bavaria 707 HBK 116 Bavaria 707 MTK 113 Bavaria 760 MTK 113 Bavaria 770 HBK 113 Bavaria 770 MTK 112 Bavaria 808 115 Bavaria 820 MTK 111 Bénéteau 25 siehe Platu 25 Blue Sail 24 N 94 Bianca 27 115 Bianca 28 111 Bianca 36 101 Big Gipsy 11,9m² 122 Big Gipsy 14m² 120 Biga 24 MTK 114 Binnenkieler 30m² V 100 Bolero 122 Bongo Kielskiff N 97 Brenta 24 Blue Sail 24 N 94 Brenta 30 N 87 Brio 23 115 C C&C 25 111 C&C 26 110 C&C 27 108 C&C 30 107 C&C 33 102 C&C 34 102 C&C 35 91 CBS 750 MTK 114 CR 25 Cruiser 97 Cadet (Jugendboot) 152 Calif 120 Caprise 113 Carina MTK + KLS 134 Carrera Formula Uno 85 Carrera Helmsman 91 Catalina22->Jaguar22 Challenger 22 SWK 124 Chaps 30 V 88 Chess N 106 Comet(ino) 700 MTK Normal 118 Comet(ino) 701 MTK 112 Comet(ino) 770 MTK 114 Comet(ino) 800 MTK 113 Comet(ino) 801 MTK 112 Comet(ino) 860 108 Commander 31 109 Condor 55 HBK 121 Condor 70 HBK 114 Conger 118 Conrad 20 123 Conrad 600 MTK 119 Conrad 760 GT 117 Contender 103 Contest 25 119 Contest 27 114 Contest 28 113 Contest 30 109 Corsair F31 Tri 92 Corsaire 123 D Daimio 116 Dart 18 84 Defender 27 111 Dehler 18 111 Dehler 22 MTK 112 Dehler 25 Cr. -
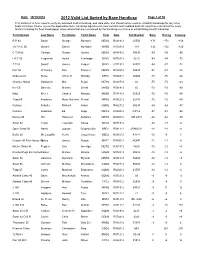
2012 Valid List Sorted by Base Handicap
Date: 10/19/2012 2012 Valid List Sorted by Base Handicap Page 1 of 30 This Valid List is to be used to verify an individual boat's handicap, and valid date, and should not be used to establish handicaps for any other boats not listed. Please review the appilication form, handicap adjustments, boat variants and modified boat list reports to understand the many factors including the fleet handicapper observations that are considered by the handicap committee in establishing a boat's handicap Yacht Design Last Name First Name Yacht Name Fleet Date Sail Number Base Racing Cruising R P 90 David George Rambler NEW2 R021912 25556 -171 -171 -156 J/V I R C 66 Meyers Daniel Numbers MHD2 R012912 119 -132 -132 -120 C T M 66 Carlson Gustav Aurora NEW2 N081412 50095 -99 -99 -90 I R C 52 Fragomen Austin Interlodge SMV2 N072412 5210 -84 -84 -72 T P 52 Swartz James Vesper SMV2 C071912 52007 -84 -87 -72 Farr 50 O' Hanley Ron Privateer NEW2 N072412 50009 -81 -81 -72 Andrews 68 Burke Arthur D Shindig NBD2 R060412 55655 -75 -75 -66 Chantier Naval Goldsmith Mat Sejaa NEW2 N042712 03 -75 -75 -63 Ker 55 Damelio Michael Denali MHD2 R031912 55 -72 -72 -60 Maxi Kiefer Charles Nirvana MHD2 R041812 32323 -72 -72 -60 Tripp 65 Academy Mass Maritime Prevail MRN2 N032212 62408 -72 -72 -60 Custom Schotte Richard Isobel GOM2 R062712 60295 -69 -69 -57 Custom Anderson Ed Angel NEW2 R020312 CAY-2 -57 -51 -36 Merlen 49 Hill Hammett Defiance NEW2 N020812 IVB 4915 -42 -42 -30 Swan 62 Tharp Twanette Glisse SMV2 N071912 -24 -18 -6 Open Class 50 Harris Joseph Gryphon Soloz NBD2 -

CD270-Manual.Pdf
CAPE DORY 270 Edited by: Catherine Monaghan, 2007 LETTER OF WELCOME Dear Skipper: Welcome to the Cape Dory fleet! You have joined the select group of sailors who recognize the quality construction and traditional workmanship found in every Cape Dory yacht. This manual has been prepared to assist you in getting to know your new yacht before setting sail for the first time. It also is a helpful guide to follow for proper care and maintenance in the future. The Cape Dory team of managers, supervisors, and quality control personnel do their very best through every step of the construction process and strive to build boats of exceptional quality which will provide their owners with many years of sailing pleasure and retain a high resale value. Please review the material carefully. You will enjoy your new Cape Dory more if you are familiar with the design and construction of the yacht and with the equipment used on board. Any questions you may have can be answered by your authorized dealer as he is a knowledgeable professional and is familiar with your new boat. He will continue to be your most important contact for information about your boat and for any problems should they develop. We appreciate your confidence in our product and assure you that with proper care, you should have many years and miles of enjoyable sailing in your new Cape Dory. Again, welcome to the fleet. May the wind always be fair. Sincerely, Andrew C. Vavolotis President Cape Dory Yachts, Inc. www.capedory.org - 2 - TABLE OF CONTENTS FORWARD & DISCLAIMER 6 CUSTOMER SERVICE 7 OWNERS RECORD 8 DEALER'S COMMISSIONING CHECKLIST 9 INTRODUCTION 13 CAPE DORY OWNERS ASSOCIATION 14 I. -

Midwinter Regatta Notice of Race February 18 & 19, 2012*
“YOUR BODY IS AN EXTENSION OF YOUR BOAT, SO MAINTAIN IT JUST AS YOU WOULD YOUR HARDWARE & SAILS” March 2011 Sailing World Neurosurgeon, Dr. Robert Bray, Jr. and colleague Peter Drasnin racing their Open 5.70 in Marina del Rey, CA. Check out the full article in the March 2011 edition of Sailing SENSIBLE SOLUTIONS FOR THE ACTIVE SAILOR SERVICES DISC Sports & Spine Center is one of America’s foremost providers • Spine Care of minimally invasive spine procedures and advanced arthroscopic • Orthopedics techniques. Dr. Robert S. Bray, Jr. founded DISC with the vision of • Sports Medicine delivering an unparalleled patient experience for those suffering from sports injuries, orthopedic issues and spine disorders in a one-stop, multi- • Pain Management disciplinary setting. With a wide range of specialists under one roof, the • Soft Tissue result is an unmatched continuity of care with more efficiency, less stress • Chiropractic Care for the patient and a zero MRSA infection rate. • Rehabilitation DISC SPORTS & SPINE CENTER Marina del Rey / Beverly Hills / Newport Beach 310.574.0400 / 866.481.DISC (3472) www.discmdgroup.com An Official Medical Services Provider of the U.S. Olympic Team The 83rd Annual SCYA Midwinter Regatta Notice of Race February 18 & 19, 2012* 1.0 RULES The regatta will be governed by the rules as defined in The Racing Rules of Sailing, 2009-2012 (“RRS”). 2.0 ELIGIBILITY AND ENTRY 2.1 Each entrant must be a member of a yacht club or sailing association belonging to the Southern California Yachting Association (SCYA), US SAILING, the Southern California Cruiser Association (SCCA), or the American Model Yacht Association (ACMYA). -

DRYA Regatta Results - DYC Regatta - (All Boats Competing Included)
DRYA Regatta Results - DYC Regatta - (all boats competing included) Originally Posted on: 2017-05-27 at approximately 17:27:52 Repost on: 2017-05-27 at 18:45:14. See notes below Race 1 notes: CLUB JAM WOULDMNOT PRINT. COMBINED WITH PRFWH. PRFWH RESULTSB AS FOLLOWS: 26226 PENDRAGON 1ST, MAJIC STAR 2ND, ADVANTAGE 3RD ALL OTHERS ARE CLUB JAM 41523 corrected finish time 150749 PRF 3 Scroll down for results Finds ways to share our sport. Invite a guest sailing." 2017-05-27 6:45 PM 1 of 7 Race 1 Results Class: PRF 1 Start Time: 11:10 Time Limit: 16:10:00 Date: Distance: 16.28 nm 1st Finish in Class: 13:42:27 Race 1 Race 1 Race 1 Race 1 Race 1 Regatta: DYC PRF Race 1 Finish Elapsed Corrected Class Sail # Boat Name Owner Club Type of Boat Rating TCF Time Time Time Place 35009 CHICO 2 Jim Weyand BYC ID 35 33 [ S ] 1.10169 13:48:25.00 02:38:25.00 02:54:31.61 1 40025 SOLUTION William H Francis BYC/GPSC FARR 40 OD MH -9 [ S ] 1.18613 13:42:27.00 02:32:27.00 03:00:49.54 2 35427 EPIC Raymond S Adams BYC BEN 42S7FRMHKITES 54 [ S ] 1.06383 14:22:48.00 03:12:48.00 03:25:06.38 3 35999 VANGUARD Michael Goran GLYC MUMM 36 ODR 42 [ S ] 1.08514 14:30:11.00 03:20:11.00 03:37:13.64 4 25669 NOT SO EZ MONEY Michael Medwid BYC DEHLER 44SQ 36 [ S ] 1.09612 14:38:10.00 03:28:10.00 03:48:10.56 5 Class: PRF 2 Start Time: 10:50 Time Limit: 15:50:00 Date: Distance: 16.28 nm 1st Finish in Class: 13:44:50 Race 1 Race 1 Race 1 Race 1 Race 1 Regatta: DYC PRF Race 1 Finish Elapsed Corrected Class Sail # Boat Name Owner Club Type of Boat Rating TCF Time Time Time Place 99 SPITFIRE -

West Crane Operation, Maintenance and Training Manual
West Crane Operation, Maintenance and Training Manual West Crane Operation, Maintenance and Training Manual 2012.11.23 v8 It is important for a Crane Operator to be instructed in the use of the crane and to understand the severe consequences of careless operation. A thorough study of the following information should provide a better understanding of safe operation and afford a greater margin of safety for people and property. The overall responsibility for the operation and maintenance of the crane lies with the Marine Facilities Director. Definitions and Requirements. "Working Load" means the external load applied to the crane, including the weight of load attaching equipment such as shackles, slings and spreader beams. "Load block" means the assembly of sheaves suspended by the hoisting rope. "Mast" means the upright member of the crane. “Hook” The crane shall be equipped with a safety latch type of hook. "Safety Hook" means a hook with a latch to prevent slings or load from accidentally slipping off the hook. "Side loading" (side pull) is a load applied at an angle to the vertical plane of the boom. "Swing" means rotation of the mast and boom for movements of loads in a horizontal direction about the axis of rotation. “Owner installed rigging” the failure of any owner installed attachment rigging, strops, lift points, bars, or angles etc. is the total responsibility of the owner. “Register” A fully completed and up-to-date register shall be kept in the office, giving the particulars and dates with respect to: • The inspections and maintenance completed. • A list of Designated Operators.