DOCSLIB.ORG

Engineering Physics I Syllabus COURSE IDENTIFICATION Course

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Engineering Physics I Syllabus COURSE IDENTIFICATION Course Engineering Physics I Syllabus COURSE IDENTIFICATION Course Prefix/Number PHYS 104 Course Title Engineering Physics I Division Applied Science Division Program Physics Credit Hours 4 credit hours Revision Date Fall 2010 Assessment Goal per Outcome(s) 70% INSTRUCTION CLASSIFICATION Academic COURSE DESCRIPTION This course is the first semester of a calculus-based physics course primarily intended for engineering and science majors. Course work includes studying forces and motion, and the properties of matter and heat. Topics will include motion in one, two, and three dimensions, mechanical equilibrium, momentum, energy, rotational motion and dynamics, periodic motion, and conservation laws. The laboratory (taken concurrently) presents exercises that are designed to reinforce the concepts presented and discussed during the lectures. PREREQUISITES AND/OR CO-RECQUISITES MATH 150 Analytic Geometry and Calculus I The engineering student should also be proficient in algebra and trigonometry. Concurrent with Phys. 140 Engineering Physics I Laboratory COURSE TEXT *The official list of textbooks and materials for this course are found on Inside NC. • COLLEGE PHYSICS, 2nd Ed. By Giambattista, Richardson, and Richardson, McGraw-Hill, 2007. • Additionally, the student must have a scientific calculator with trigonometric functions. COURSE OUTCOMES • To understand and be able to apply the principles of classical Newtonian mechanics. • To effectively communicate classical mechanics concepts and solutions to problems, both in written English and through mathematics. • To be able to apply critical thinking and problem solving skills in the application of classical mechanics. To demonstrate successfully accomplishing the course outcomes, the student should be able to: 1) Demonstrate knowledge of physical concepts by their application in problem solving. Competencies: a) Use significant digits appropriately in calculations; b) Apply algebra and trigonometry (including graphical techniques) in problem solving applications; c) Solve problems regarding counting and measuring; d) Solve problems regarding the mechanics of forces and motion, using appropriate terminology, units, and equations; e) Solve problems regarding the mechanical and thermal properties of matter. 2) Formulate problems using mathematical tools: Competencies: The student will be able to: a) Use significant digits appropriately in calculations; b) Distinguish between accuracy and precision in measurements; c) Apply algebra and trigonometry in problem solving applications; and d) Demonstrate the ability communicate ideas and facts using equations, graphs, and other symbolic tools COURSE OUTLINE 1) Introduction to Physics a) The use of mathematics b) Dimensions analysis and units c) Scientific notation and significant digits d) graphs 2) Straight Line Motion a) Velocity and acceleration b) Equations for uniformly accelerated motion c) Examples and applications d) Relative velocity 3) Curved Motion a) Uniform circular motion b) Projectile motion 4) Newton’s Laws a) The three laws b) Using the laws (force diagrams, also known as free body diagrams) c) First equilibrium condition (relating to forces that would cause motion in a straight line) d) Second equilibrium condition (rotational motion) 5) Work, Power, and Energy 2 a) Work and energy b) Power c) Conservation of Energy d) Simple machines 6) Linear Momentum a) Linear momentum and Newton’s 2nd Law b) Collisions c) Momentum and the center of mass 7) Angular Motion a) Angular analogs to linear concepts and equations b) Centripetal (not centrifugal) motion c) Rotational work and energy d) Angular momentum and conservation of angular momentum 8) States of Matter, a) Density b) Elastic modulus and pressure c) Wave principles 9) Fluids 10) Archimedes’ principle 11) Pascal’s law and Bernoulli’s equation 12) Laminar and turbulent flow INSTRUCTIONAL METHODS A variety of teaching methods will be used that includes lectures, discussions, and demonstrations. A variety of audio-visual presentations will be used as appropriate to help stress important concepts. Additional handouts will be provided. Each student should obtain the textbook presented in this syllabus’s TEXT section. GRADING SCALE 90 – 100 % → A 80 – 89 % → B 70 – 79 % → C 60 – 69 % → D Below 60% → F ASSESSMENT OF STUDENT GAIN 1. Quizzes: Announced and un-announced quizzes will be given in class. There are no make-up for missed quizzes. 2. Homework assignments: Students will be expected to complete and return assigned homework by due date. 3. Exams: There will be a total of five exams given throughout the semester. The fifth exam will be cumulative and administered as a final exam for the course. 3 ATTENDANCE POLICY Absences that occur due to students participating in official college activities are excused except in those cases where outside bodies, such as the State Board of Nursing, have requirements for minimum class minutes for each student. Students who are excused will be given reasonable opportunity to make up any missed work or receive substitute assignments from the instructor and should not be penalized for the absence. Proper procedure should be followed in notifying faculty in advance of the student’s planned participation in the event. Ultimately it is the student’s responsibility to notify the instructor in advance of the planned absence. Unless students are participating in a school activity or are excused by the instructor, they are expected to attend class. If a student’s absences exceed seventy five (75) minutes per credit hour for the course or, in the case of on-line or other non-traditional courses, the student is inactive for one-eighth of the total course duration, the instructor has the right, but is not required, to withdraw a student from the course. Once the student has been dropped for excessive absences, the registrar’s office will send a letter to the student, stating that he or she has been withdrawn. Alternatively, the faculty member may summarily issue the grade of “F” to any student whose absences exceed the above amounts. The normal appeal process may be utilized by the student. ACADEMIC INTEGRITY NCCC expects every student to demonstrate ethical behavior with regard to academic pursuits. Academic integrity in coursework is a specific requirement. Definitions, examples, and possible consequences for violations of Academic Integrity, as well as the appeals process, can be found in the College Catalog, Student Handbook, and/or Code of Student Conduct and Discipline. CELL PHONE POLICY Student cell phones and pagers must be turned off during class times. Faculty may approve an exception for special circumstances. NOTES: • The information and statements contained in this document are subject to change at the discretion of the instructor and NCCC. Changes will be published in writing and made available to students • All the written materials given to students’ remains a property of NCCC. NOTE: If you are a student with a disability who may need accommodation(s) under the Americans with Disabilities Act (ADA), please notify the Dean of Student Development, Chanute 4 Campus, Student Union, 620-431-2820, Ext. 213., or the Dean, Ottawa Campus, 785-242-2607 ext 312, as soon as possible. You will need to bring your documentation for review in order to determine reasonable accommodations, and then we can assist you in arranging any necessary accommodations. 5 .
Load more

Recommended publications
  • Glossary Physics (I-Introduction)
    1 Glossary Physics (I-introduction) - Efficiency: The percent of the work put into a machine that is converted into useful work output; = work done / energy used [-]. = eta In machines: The work output of any machine cannot exceed the work input (<=100%); in an ideal machine, where no energy is transformed into heat: work(input) = work(output), =100%. Energy: The property of a system that enables it to do work. Conservation o. E.: Energy cannot be created or destroyed; it may be transformed from one form into another, but the total amount of energy never changes. Equilibrium: The state of an object when not acted upon by a net force or net torque; an object in equilibrium may be at rest or moving at uniform velocity - not accelerating. Mechanical E.: The state of an object or system of objects for which any impressed forces cancels to zero and no acceleration occurs. Dynamic E.: Object is moving without experiencing acceleration. Static E.: Object is at rest.F Force: The influence that can cause an object to be accelerated or retarded; is always in the direction of the net force, hence a vector quantity; the four elementary forces are: Electromagnetic F.: Is an attraction or repulsion G, gravit. const.6.672E-11[Nm2/kg2] between electric charges: d, distance [m] 2 2 2 2 F = 1/(40) (q1q2/d ) [(CC/m )(Nm /C )] = [N] m,M, mass [kg] Gravitational F.: Is a mutual attraction between all masses: q, charge [As] [C] 2 2 2 2 F = GmM/d [Nm /kg kg 1/m ] = [N] 0, dielectric constant Strong F.: (nuclear force) Acts within the nuclei of atoms: 8.854E-12 [C2/Nm2] [F/m] 2 2 2 2 2 F = 1/(40) (e /d ) [(CC/m )(Nm /C )] = [N] , 3.14 [-] Weak F.: Manifests itself in special reactions among elementary e, 1.60210 E-19 [As] [C] particles, such as the reaction that occur in radioactive decay.
    [Show full text]
  • Department of Physics College of Arts and Sciences Physics
    DEPARTMENT OF PHYSICS COLLEGE OF ARTS AND SCIENCES PHYSICS Faculty I. Major in Physics—38 hours William Nettles (2006). Professor of Physics, Department A. Physics 231-232, 311, 313, 314, 420, 424(1-3 Chair, and Associate Dean of the College of Arts and hours), 430, 498—28–30 hours Sciences. B.S., Mississippi College; M.S., and Ph.D., B. Select three or more courses: PHY 262, 325, 350, Vanderbilt University. 360, 395-6-7*, 400, 410, 417, 425 (1-2 hours**), 495* Ildefonso Guilaran (2008). Associate Professor of Physics. C. Prerequisites: MAT 211, 212, 213, 314 B.S., Western Kentucky University; M.S. and Ph.D., *Must be approved Special/Independent Studies Florida State University. **Maximum 3 hours from 424 and 425 apply to major. Geoffrey Poore (2010). Assistant Professor of Physics. B.A., II. Major in Physical Science—44 hours Wheaton College; M.S. and Ph.D., University of Illinois. A. CHE 111, 112, 113, 211, 221—15 hours David A. Ward (1992, 1999). Professor of Physics, B.S. B. PHY 112, 231-32, 311, 310 or 301—22 hours and M.A., University of South Florida; Ph.D., North C. Upper Level Electives from CHE and PHY—7 Carolina State University. hours; maximum 1 hour from 424 and 1 from 498 III. Minor in Physics—24 semester hours Staff Physics 231-232, 311, + 10 hours of Physics electives Christine Rowland (2006). Academic Secretary— except PHY 111, 112, 301, 310 Engineering, Physics, Math, and Computer Science. IV. Teacher Licensure in Physics (Grades 6–12) A. Complete the requirements shown above for the Physics or Physical Science major.
    [Show full text]
  • Fundamentals of Particle Physics
    Fundamentals of Par0cle Physics Particle Physics Masterclass Emmanuel Olaiya 1 The Universe u The universe is 15 billion years old u Around 150 billion galaxies (150,000,000,000) u Each galaxy has around 300 billion stars (300,000,000,000) u 150 billion x 300 billion stars (that is a lot of stars!) u That is a huge amount of material u That is an unimaginable amount of particles u How do we even begin to understand all of matter? 2 How many elementary particles does it take to describe the matter around us? 3 We can describe the material around us using just 3 particles . 3 Matter Particles +2/3 U Point like elementary particles that protons and neutrons are made from. Quarks Hence we can construct all nuclei using these two particles -1/3 d -1 Electrons orbit the nuclei and are help to e form molecules. These are also point like elementary particles Leptons We can build the world around us with these 3 particles. But how do they interact. To understand their interactions we have to introduce forces! Force carriers g1 g2 g3 g4 g5 g6 g7 g8 The gluon, of which there are 8 is the force carrier for nuclear forces Consider 2 forces: nuclear forces, and electromagnetism The photon, ie light is the force carrier when experiencing forces such and electricity and magnetism γ SOME FAMILAR THE ATOM PARTICLES ≈10-10m electron (-) 0.511 MeV A Fundamental (“pointlike”) Particle THE NUCLEUS proton (+) 938.3 MeV neutron (0) 939.6 MeV E=mc2. Einstein’s equation tells us mass and energy are equivalent Wave/Particle Duality (Quantum Mechanics) Einstein E
    [Show full text]
  • Engineering Physics
    COLLEGE OF ENGINEERING Engineering Physics WHY ENGINEERING PHYSICS? graduates have gone on to become the CEO Engineering is about the way things work. of Eastman Kodak Co., work as acoustical Physics is about why things work the way engineers for Disney, work for the CIA, thrive they do. By combining the two, engineering in the financial sector, work in nuclear physics students are able to satisfy their engineering at Seabrook Nuclear Power Plant, curiosity and ultimately gain a deeper manage the power flow for northern New understanding of the engineering problems England, work as radiation physicists at medical centers, and become high-level UM aine’s ADVANTAGE they are working to solve. executives at SanDisk and Avis. • Professors with Ph.D. degrees, not graduate WHY STUDY ENGINEERING PHYSICS AT UMAINE? RESEARCH OPPORTUNITIES students, teach classes UMaine engineering physics was the first UMaine engineering physics students are able • State-of-the-art teaching and accredited engineering physics program in to take advantage of a myriad of research research facilities the world. Currently, it is one of only 20 programs in the U.S. and the only opportunities as undergraduates — some as • Small, student-centered accredited one in New England. e early as their freshman year. Many work classes Department of Physics and Astronomy in closely with scientists in UMaine’s Laboratory for Surface Science and Technology, which is • Opportunities to do conjunction with the College of Engineering undergraduate research offers bachelor’s and master’s degrees in internationally known for cutting-edge alongside faculty engineering physics. e curriculum research with sensors.
    [Show full text]
  • A Brief History and Philosophy of Mechanics
    A Brief History and Philosophy of Mechanics S. A. Gadsden McMaster University, [email protected] 1. Introduction During this period, several clever inventions were created. Some of these were Archimedes screw, Hero of Mechanics is a branch of physics that deals with the Alexandria’s aeolipile (steam engine), the catapult and interaction of forces on a physical body and its trebuchet, the crossbow, pulley systems, odometer, environment. Many scholars consider the field to be a clockwork, and a rolling-element bearing (used in precursor to modern physics. The laws of mechanics Roman ships). [5] Although mechanical inventions apply to many different microscopic and macroscopic were being made at an accelerated rate, it wasn’t until objects—ranging from the motion of electrons to the after the Middle Ages when classical mechanics orbital patterns of galaxies. [1] developed. Attempting to understand the underlying principles of 3. Classical Period (1500 – 1900 AD) the universe is certainly a daunting task. It is therefore no surprise that the development of ‘idea and thought’ Classical mechanics had many contributors, although took many centuries, and bordered many different the most notable ones were Galileo, Huygens, Kepler, fields—atomism, metaphysics, religion, mathematics, Descartes and Newton. “They showed that objects and mechanics. The history of mechanics can be move according to certain rules, and these rules were divided into three main periods: antiquity, classical, and stated in the forms of laws of motion.” [1] quantum. The most famous of these laws were Newton’s Laws of 2. Period of Antiquity (800 BC – 500 AD) Motion, which accurately describe the relationships between force, velocity, and acceleration on a body.
    [Show full text]
  • Classical Mechanics
    Classical Mechanics Hyoungsoon Choi Spring, 2014 Contents 1 Introduction4 1.1 Kinematics and Kinetics . .5 1.2 Kinematics: Watching Wallace and Gromit ............6 1.3 Inertia and Inertial Frame . .8 2 Newton's Laws of Motion 10 2.1 The First Law: The Law of Inertia . 10 2.2 The Second Law: The Equation of Motion . 11 2.3 The Third Law: The Law of Action and Reaction . 12 3 Laws of Conservation 14 3.1 Conservation of Momentum . 14 3.2 Conservation of Angular Momentum . 15 3.3 Conservation of Energy . 17 3.3.1 Kinetic energy . 17 3.3.2 Potential energy . 18 3.3.3 Mechanical energy conservation . 19 4 Solving Equation of Motions 20 4.1 Force-Free Motion . 21 4.2 Constant Force Motion . 22 4.2.1 Constant force motion in one dimension . 22 4.2.2 Constant force motion in two dimensions . 23 4.3 Varying Force Motion . 25 4.3.1 Drag force . 25 4.3.2 Harmonic oscillator . 29 5 Lagrangian Mechanics 30 5.1 Configuration Space . 30 5.2 Lagrangian Equations of Motion . 32 5.3 Generalized Coordinates . 34 5.4 Lagrangian Mechanics . 36 5.5 D'Alembert's Principle . 37 5.6 Conjugate Variables . 39 1 CONTENTS 2 6 Hamiltonian Mechanics 40 6.1 Legendre Transformation: From Lagrangian to Hamiltonian . 40 6.2 Hamilton's Equations . 41 6.3 Configuration Space and Phase Space . 43 6.4 Hamiltonian and Energy . 45 7 Central Force Motion 47 7.1 Conservation Laws in Central Force Field . 47 7.2 The Path Equation .
    [Show full text]
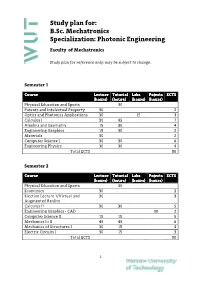
  • B.Sc. Mechatronics Specialization: Photonic Engineering
    Study plan for: B.Sc. Mechatronics Specialization: Photonic Engineering Faculty of Mechatronics Study plan for reference only; may be subject to change. Semester 1 Course Lecture Tutorial Labs Pojects ECTS (hours) (hours) (hours) (hours) Physical Education and Sports 30 Patents and Intelectual Property 30 2 Optics and Photonics Applications 30 15 3 Calculus I 30 45 7 Algebra and Geometry 15 30 4 Engineering Graphics 15 30 2 Materials 30 2 Computer Science I 30 30 6 Engineering Physics 30 30 4 Total ECTS 30 Semester 2 Course Lecture Tutorial Labs Pojects ECTS (hours) (hours) (hours) (hours) Physical Education and Sports 30 Economics 30 2 Elective Lecture 1/Virtual and 30 3 Augmented Reality Calculus II 30 30 5 Engineering Graphics ‐ CAD 30 2 Computer Science II 15 15 5 Mechanics I i II 45 45 6 Mechanics of Structures I 30 15 4 Electric Circuits I 30 15 3 Total ECTS 30 1 Study Plan for B.Sc. Mechatronics (Spec. Photonic Engineering) Semester 3 Course Lecture Tutorial Labs Pojects ECTS (hours) (hours) (hours) (hours) Physical Education and Sports 30 0 Foreign Language 60 4 Elective Lecture 2/Introduction to 30 3 MEMS Calculus III 15 30 6 Mechanics of Structures II 15 15 4 Manufacturing Technology I 30 4 Fine Machine Design I 15 30 3 Electric Circuits II 30 3 Basics of Automation and Control I 30 15 4 Total ECTS 31 Semester 4 Course Lecture Tutorial Labs Pojects ECTS (hours) (hours) (hours) (hours) Physical Education and Sports 30 Foreign Language 60 4 Elective Lecture 3/Photographic 30 3 techniques in image acqusition Elective Lecture 4 30 3 /Enterpreneurship Optomechatronics 30 30 5 Electronics I 15 15 2 Electronics II 15 1 Fine Machine Design II 15 15 3 Manufacturing Technology 30 2 Metrology 30 30 4 Total ECTS 27 Semester 5 Course Lecture Tutorial Labs Pojects ECTS (hours) (hours) (hours) (hours) Physical Education and Sports 30 0 Foreign Language 60 4 Marketing 30 2 Elective Lecture 5/ Electric 30 2 2 Study Plan for B.Sc.
    [Show full text]
  • Exercises in Classical Mechanics 1 Moments of Inertia 2 Half-Cylinder
    Exercises in Classical Mechanics CUNY GC, Prof. D. Garanin No.1 Solution ||||||||||||||||||||||||||||||||||||||||| 1 Moments of inertia (5 points) Calculate tensors of inertia with respect to the principal axes of the following bodies: a) Hollow sphere of mass M and radius R: b) Cone of the height h and radius of the base R; both with respect to the apex and to the center of mass. c) Body of a box shape with sides a; b; and c: Solution: a) By symmetry for the sphere I®¯ = I±®¯: (1) One can ¯nd I easily noticing that for the hollow sphere is 1 1 X ³ ´ I = (I + I + I ) = m y2 + z2 + z2 + x2 + x2 + y2 3 xx yy zz 3 i i i i i i i i 2 X 2 X 2 = m r2 = R2 m = MR2: (2) 3 i i 3 i 3 i i b) and c): Standard solutions 2 Half-cylinder ϕ (10 points) Consider a half-cylinder of mass M and radius R on a horizontal plane. a) Find the position of its center of mass (CM) and the moment of inertia with respect to CM. b) Write down the Lagrange function in terms of the angle ' (see Fig.) c) Find the frequency of cylinder's oscillations in the linear regime, ' ¿ 1. Solution: (a) First we ¯nd the distance a between the CM and the geometrical center of the cylinder. With σ being the density for the cross-sectional surface, so that ¼R2 M = σ ; (3) 2 1 one obtains Z Z 2 2σ R p σ R q a = dx x R2 ¡ x2 = dy R2 ¡ y M 0 M 0 ¯ 2 ³ ´3=2¯R σ 2 2 ¯ σ 2 3 4 = ¡ R ¡ y ¯ = R = R: (4) M 3 0 M 3 3¼ The moment of inertia of the half-cylinder with respect to the geometrical center is the same as that of the cylinder, 1 I0 = MR2: (5) 2 The moment of inertia with respect to the CM I can be found from the relation I0 = I + Ma2 (6) that yields " µ ¶ # " # 1 4 2 1 32 I = I0 ¡ Ma2 = MR2 ¡ = MR2 1 ¡ ' 0:3199MR2: (7) 2 3¼ 2 (3¼)2 (b) The Lagrange function L is given by L('; '_ ) = T ('; '_ ) ¡ U('): (8) The potential energy U of the half-cylinder is due to the elevation of its CM resulting from the deviation of ' from zero.
    [Show full text]
  • Euler and the Dynamics of Rigid Bodies Sebastià Xambó Descamps
    Euler and the dynamics of rigid bodies Sebastià Xambó Descamps Abstract. After presenting in contemporary terms an outline of the kinematics and dynamics of systems of particles, with emphasis in the kinematics and dynamics of rigid bodies, we will consider briefly the main points of the historical unfolding that produced this understanding and, in particular, the decisive role played by Euler. In our presentation the main role is not played by inertial (or Galilean) observers, but rather by observers that are allowed to move in an arbitrary (smooth, non-relativistic) way. 0. Notations and conventions The material in sections 0-6 of this paper is an adaptation of parts of the Mechanics chapter of XAMBÓ-2007. The mathematical language used is rather standard. The read- er will need a basic knowledge of linear algebra, of Euclidean geometry (see, for exam- ple, XAMBÓ-2001) and of basic calculus. 0.1. If we select an origin in Euclidean 3-space , each point can be specified by a vector , where is the Euclidean vector space associated with . This sets up a one-to-one correspondence between points and vectors . The inverse map is usually denoted . Usually we will speak of “the point ”, instead of “the point ”, implying that some point has been chosen as an origin. Only when conditions on this origin become re- levant will we be more specific. From now on, as it is fitting to a mechanics context, any origin considered will be called an observer. When points are assumed to be moving with time, their movement will be assumed to be smooth.
    [Show full text]
  • Engineering Physics I & Ii
    ENGINEERING PHYSICS I & II DIPLOMA COURSE IN ENGINEERING FIRST AND SECOND SEMESTER A Publication under Government of Tamilnadu Distribution of Free Textbook Programme (NOT FOR SALE) Untouchability is a sin Untouchability is a crime Untouchability is a inhuman DIRECTORATE OF TECHNICAL EDUCATION GOVERNMENT OF TAMILNADU Government of Tamilnadu First Edition – 2015 THIRU. PRAVEEN KUMAR I.A.S Principal Secretary / Commissioner of Technical Education Directorate of Technical Education Guindy, Chennai- 600025 Dr. K.SUNDARAMOORTHY, M.E., Phd., Additional Director of Technical Education (Polytechnics) Directorate of Technical Education Guindy, Chennai- 600025 Co-ordinator Convener Er. R.SORNAKUMAR M.E., THIRU. K.SELVARAJAN M.Sc., Principal HOD (UG) / Physics Dr. Dharmambal Government Institute of Chemical Technology Polytechnic College for Women Tharamani, Chennai—113 Tharamani, Chennai—113 Reviewer Dr.K.SIVAKUMAR, M.Sc., Phd., Professor of Physics and Dean, Regional office Anna University, Madurai—7. Authors Dr.K.RAJESEKAR, M.Sc., Phd., Lecturer (UG)/ Physics Government Polytechnic College Nagercoil THIRU.G.MOHANA SUNDARAM, M.Sc.,M.Phil.,M.Ed., THIRU S.NAGARAJAN, M.Sc., HOD(UG)/Physics HOD(UG)/ Physics Central Polytechnic College Government Polytechnic College, Taramani, Chennai-113. Purasaiwakkam, Chennai –12 THIRU.N.SARAVANAN, M.Sc.,M.Phil,M.Ed., TMT.G.INDIRA, M.Sc.,M.Phil., HOD(UG)/Physics Lecturer/Physics Meenakshi Krishnan Polytechnic College Dr. Dharmambal Government Pammal, Chennai—75 Polytechnic College for Women Tharamani, Chennai—113 This book has been prepared by the Directorate of Technical Education This book has been printed on 60 G.S.M Paper Through the Tamil Nadu Text book and Educational Services Corporation ii FOREWORD With the concept of Global Village after liberalisation and globalisation, our country India has become one of the most sought after destinations by many Multi National Companies for investment.
    [Show full text]
  • The Universe As a Laboratory: Fundamental Physics
    The Universe as a Laboratory: Fundamental Physics The universe serves as an unparalleled laboratory for frontier physics, providing extreme conditions and unique opportunities to test theoretical models. Astronomical observations can yield invaluable information for physicists across the entire spectrum of the science, studying everything from the smallest constituents of mat- ter to the largest known structures. Astronomy is the principal player in the quest to uncover the full story about the origin, evolution and ultimate fate of the universe. The earliest “baby picture” of the universe is the map of the cosmic microwave background (CMB) radiation, predicted in 1948 and discovered in 1964. For years, physicists insisted that this radiation, seen coming from all directions in space, had to have irregularities in order for the universe as we know it to exist. These irregularities were not discovered until the COBE satellite mapped the radiation in 1992. Later, the WMAP satellite refined the measurement, allowing cosmologists to pinpoint the age of the universe at 13.7 billion years. Continued studies, including ground-based observations, seek to glean clues from the CMB about the basic nature of the universe and of its fundamental constituents. New telescopes and new technology promise to give astronomers better information about extremely distant objects—objects seen as they were in the early history of the universe. This, in turn, will provide valuable clues about how the first stars and galaxies developed and evolved into the objects we see in the universe today. The biggest mysteries in physics—and the biggest challenges for cosmologists—are the nature of dark matter and dark energy, which together constitute 95 percent of the universe.
    [Show full text]
  • NGSS Physics in the Universe
    Standards-Based Education Priority Standards NGSS Physics in the Universe 11th Grade HS-PS2-1: Analyze data to support the claim that Newton’s second law of motion describes PS 1 the mathematical relationship among the net force on a macroscopic object, its mass, and its acceleration. HS-PS2-2: Use mathematical representations to support the claim that the total momentum of PS 2 a system of objects is conserved when there is no net force on the system. HS-PS2-3: Apply scientific and engineering ideas to design, evaluate, and refine a device that PS 3 minimizes the force on a macroscopic object during a collision. HS-PS2-4: Use mathematical representations of Newton’s Law of Gravitation and Coulomb’s PS 4 Law to describe and predict the gravitational and electrostatic forces between objects. HS-PS2-5: Plan and conduct an investigation to provide evidence that an electric current can PS 5 produce a magnetic field and that a changing magnetic field can produce an electric current. HS-PS3-1: Create a computational model to calculate the change in energy of one PS 6 component in a system when the change in energy of the other component(s) and energy flows in and out of the system are known/ HS-PS3-2: Develop and use models to illustrate that energy at the macroscopic scale can be PS 7 accounted for as either motions of particles or energy stored in fields. HS-PS3-3: Design, build, and refine a device that works within given constraints to convert PS 8 one form of energy into another form of energy.
    [Show full text]