DOCSLIB.ORG

Lecture Notes for PHY 405 Classical Mechanics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Lecture Notes for PHY 405 Classical Mechanics Lecture Notes for PHY 405 Classical Mechanics From Thorton & Marion's Classical Mechanics Prepared by Dr. Joseph M. Hahn Saint Mary's University Department of Astronomy & Physics November 25, 2003 revised November 29 Chapter 11: Dynamics of Rigid Bodies rigid body = a collection of particles whose relative positions are fixed. We will ignore the microscopic thermal vibrations occurring among a `rigid' body's atoms. The inertia tensor Consider a rigid body that is composed of N particles. Give each particle an index α = 1 : : : N. Particle α has a velocity vf,α measured in the fixed reference frame and velocity vr,α = drα=dt in the reference frame that rotates about axis !~ . Then according to Eq. 10.17: vf,α = V + vr,α + !~ × rα where V = velocity of the moving origin relative to the fixed origin. Note that the particles in a rigid body have zero relative velocity, ie, vr,α = 0. 1 Thus vα = V + !~ × rα after dropping the f subscript 1 1 and T = m v2 = m (V + !~ × r )2 is the particle's KE α 2 α α 2 α α N so T = Tα the system's total KE is α=1 X1 1 = MV2 + m V · (!~ × r ) + m (!~ × r )2 2 α α 2 α α α α X X 1 1 = MV2 + V · !~ × m r + m (!~ × r )2 2 α α 2 α α α ! α X X where M = α mα = the system's total mass. P Now choose the system's center of mass R as the origin of the moving frame. 0 Since rα = R + rα is α's position in the fixed reference frame, 0 ) R = α mαrα=M = α mα(R + rα)=M = R + α mαrα=M. ) m r = 0 and the middle term in T is zero: α Pα α P P P thus T = Ttrans + Trot 1 where T = MV2 = KE due to system's translation trans 2 1 and T = m (!~ × r )2 = KE due to system's rotation rot 2 α α α X Now focus on Trot, and note that (A × B)2 = A2B2 − (A · B)2 see page 28 for proof. 2 Thus 1 T = m [!2r2 − (!~ · r )2] rot 2 α α α α X In Cartesian coordinates, !~ = !xx^ + !yy^ + !z^z 3 2 2 2 2 2 so ! = !x + !y + !z ≡ !i i=1 3 X and rα = xα;ix^i i=1 X3 so !~ · rα = !ixα;i i=1 X Thus 1 3 3 3 3 T = m !2 x2 − ! x ! x rot 2 α 2 i α;k i α;i 0 j α;j13 α i=1 ! ! i=1 ! j=1 X X Xk=1 X X 4 @ A5 We can also write 3 !i = !jδi;j j=1 X 1 i = j where δ = i;j 0 i 6= j 3 3 2 so !i = !i !jδi;j = !i!jδi;j j=1 j=1 X X and also note that ai bi = aibi ≡ aibi i ! i ! i j i;j X X X X X 3 1 3 so T = m ! ! δ x2 − ! ! x x rot 2 α 2 i j i;j α;k i j α;i α;j3 α i;j ! i;j X X Xk=1 X 3 1 4 5 = m ! ! δ x2 − x x 2 α i j i;j α;k α;i α;j α i;j " # X X Xk=1 3 1 = ! ! m δ x2 − x x 2 i j α i;j α;k α;i α;j i;j α " # X X Xk=1 3 3 1 ≡ I ! ! 2 i;j i j i=1 j=1 X X 3 2 where Ii;j ≡ mα δi;j xα;k − xα;ixα;j α " # X Xk=1 are the 9 elements of a 3 × 3 matrix called the inertial tensor fIg. 2 Note that the Ii;j has units of mass×length . Since xα;1 = xα, xα;2 = yα, xα;3 = zα, 2 2 α mα(yα + zα) − α mαxαyα − α mαxαzα fIg = − m y x m (x2 + z2) − m y z 8 P α α α α α Pα α α Pα α α α 9 − m z x − m z y m (x2 + y2 ) < Pα α α α P α α α α α Pα α α = : P P P ; Be sure to write your matrix elements Ii;j consistently; here, the i index increments down along a column while the j index increments across a row. Also note that Ii;j = Ij;i ) the inertia tensor is symmetric. The diagonal elements Ii;i = the moments of inertia while the off–diagonal elements Ii=6 j =the products of inertia 4 For a continuous body having a density ρ(r), 3 2 dIi;j ! δi;j xk − xixj dm ! Xk=1 = the contribution to Ii;j due to mass element dm = ρdV 3 2 thus Ii;j = dIi;j = ρ(r) δi;j xk − xixj dV V V ! Z Z Xk=1 where the integration proceeds over the system's volume V . Example 11.3 Calculate fIg for a cube of mass M and width b and uniform density ρ = M=b3. Place the origin at one corner of the cube. Fig. 11-3. 5 b b b 2 2 2 2 I1;1 = ρ dx dy dz(x + y + z − x ) Z0 Z0 Z0 b 1 = ρb dy(y2b + b3) 0 3 Z1 1 = ρb( b4 + b4) 3 3 2 2 = ρb5 = Mb2 3 3 It is straightforward to show that the other diagonal elements are I2;2 = I3;3 = I1;1. The off–diagonal elements are similarly identical: b b b I1;2 = −ρ dx dy dz · xy Z0 Z0 Z0 1 1 1 1 = −ρ b2 b2 b = − ρb5 = − Mb2 2 2 4 4 = Ii=6 j Thus this cube has an inertia tensor 2=3 −1=4 −1=4 fIg = Mb2 −1=4 2=3 −1=4 8 9 < −1=4 −1=4 2=3 = : ; 6 Principal Axes of Inertia The axes x^i that diagonalizes a body's inertia tensor fIg is called the principal axes of inertia. In this case Ii;j = Iiδi;j 3 3 1 so T = I ! ! = rotational KE rot 2 i;j i j i=1 j=1 X X 1 3 = I !2 2 i i i=1 X where the three Ii are the body's principal moments of inertia. If this body is also rotating about one of its principal axis, say, the ^z, then !~ = !^z and 1 T = I !2 rot 2 z which is the familiar formula for the rotational KE in terms of inertia Iz found in the elementary textbooks. 1 2 )those formulae with Trot = 2I! are only valid when the rotation axis !~ lies along one of the body's three principal axes. The procedure for determining the orientation of a body's principal axes of inertia is given in Section 11.5. 7 Angular Momentum The system's total angular momentum relative to the moving/rotating origin Orot is L = mαrα × vα α X where rα and vα are α'a position and velocity relative to Orot. Recall that vα = !~ × rα (Eqn. 10.17), so L = mαrα × (!~ × rα) α X Chapter 1 and problem 1-22 show that A × (B × A) = A2B − (A · B)A 2 so L = mα[rα!~ − (rα · !~ )rα] α X and the ith component of L is 2 Li = mα[rα!i − (rα · !~ )xα;i] α X And again use 3 3 3 2 2 rα = xα;k rα · !~ = xα;j!j !i = !jδi;j j=1 j=1 Xk=1 X X 8 So 3 3 3 L = m x2 ! δ − x ! x i α 0 α;k j i;j α;j j α;i1 α j=1 j=1 X Xk=1 X X 3 @ 3 A 2 = !j mα δi;j xα;k − xα;ixα;j j=1 α ! X X Xk=1 3 = Iij!j j=1 X where the Ii;j are the elements of the inertial tensor fIg. Note that 3 3 3 L = Lix^i = Iij!jx^i i=1 i=1 j=1 X X X = fIg · !~ Lets confirm this last step by explicitly doing the matrix multiplication: L1 I11 I12 I13 !1 L = I I I ! 0 2 1 0 21 22 23 1 0 2 1 L3 I31 I32 I33 !3 @ A @ A @ A I11!1 + I12!2 + I13!3 j I1j!j = I ! + I ! + I ! = I ! 0 21 1 22 2 23 3 1 0 Pj 2j j 1 I31!1 + I32!2 + I33!3 j I3j!j B P C @ A @ A which confirms L = fIg · !~ . P Evidently the inertia tensor related the system's angular momentum L to its rotation !~ . 9 Now examine 3 3 3 1 1 1 ! L = !~ · L = I ! ! 2 i i 2 2 ij i j i=1 i=1 j=1 X X X = Trot = the body's KE due to its rotation 1 1 ) T = !~ · L = !~ · fIg · !~ rot 2 2 Note that the RHS is a scalar (as is should) since fIg · !~ is a vector, and a vector·vector = scalar. Chapter 9 showed that if an external torque N is applied to the body, then dL N = = fIg · !~_ dt since fIg is a constant. We now have several methods available for obtaining the equation of motion: Newton's Laws, Lagrange equations, Hamilton's equation, and N = fIg · !~_ (which follows from Newton's Laws) the latter equation is usually quite handy for rotating rigid bodies.
Load more

Recommended publications
  • Glossary Physics (I-Introduction)
    1 Glossary Physics (I-introduction) - Efficiency: The percent of the work put into a machine that is converted into useful work output; = work done / energy used [-]. = eta In machines: The work output of any machine cannot exceed the work input (<=100%); in an ideal machine, where no energy is transformed into heat: work(input) = work(output), =100%. Energy: The property of a system that enables it to do work. Conservation o. E.: Energy cannot be created or destroyed; it may be transformed from one form into another, but the total amount of energy never changes. Equilibrium: The state of an object when not acted upon by a net force or net torque; an object in equilibrium may be at rest or moving at uniform velocity - not accelerating. Mechanical E.: The state of an object or system of objects for which any impressed forces cancels to zero and no acceleration occurs. Dynamic E.: Object is moving without experiencing acceleration. Static E.: Object is at rest.F Force: The influence that can cause an object to be accelerated or retarded; is always in the direction of the net force, hence a vector quantity; the four elementary forces are: Electromagnetic F.: Is an attraction or repulsion G, gravit. const.6.672E-11[Nm2/kg2] between electric charges: d, distance [m] 2 2 2 2 F = 1/(40) (q1q2/d ) [(CC/m )(Nm /C )] = [N] m,M, mass [kg] Gravitational F.: Is a mutual attraction between all masses: q, charge [As] [C] 2 2 2 2 F = GmM/d [Nm /kg kg 1/m ] = [N] 0, dielectric constant Strong F.: (nuclear force) Acts within the nuclei of atoms: 8.854E-12 [C2/Nm2] [F/m] 2 2 2 2 2 F = 1/(40) (e /d ) [(CC/m )(Nm /C )] = [N] , 3.14 [-] Weak F.: Manifests itself in special reactions among elementary e, 1.60210 E-19 [As] [C] particles, such as the reaction that occur in radioactive decay.
    [Show full text]
  • A Brief History and Philosophy of Mechanics
    A Brief History and Philosophy of Mechanics S. A. Gadsden McMaster University, [email protected] 1. Introduction During this period, several clever inventions were created. Some of these were Archimedes screw, Hero of Mechanics is a branch of physics that deals with the Alexandria’s aeolipile (steam engine), the catapult and interaction of forces on a physical body and its trebuchet, the crossbow, pulley systems, odometer, environment. Many scholars consider the field to be a clockwork, and a rolling-element bearing (used in precursor to modern physics. The laws of mechanics Roman ships). [5] Although mechanical inventions apply to many different microscopic and macroscopic were being made at an accelerated rate, it wasn’t until objects—ranging from the motion of electrons to the after the Middle Ages when classical mechanics orbital patterns of galaxies. [1] developed. Attempting to understand the underlying principles of 3. Classical Period (1500 – 1900 AD) the universe is certainly a daunting task. It is therefore no surprise that the development of ‘idea and thought’ Classical mechanics had many contributors, although took many centuries, and bordered many different the most notable ones were Galileo, Huygens, Kepler, fields—atomism, metaphysics, religion, mathematics, Descartes and Newton. “They showed that objects and mechanics. The history of mechanics can be move according to certain rules, and these rules were divided into three main periods: antiquity, classical, and stated in the forms of laws of motion.” [1] quantum. The most famous of these laws were Newton’s Laws of 2. Period of Antiquity (800 BC – 500 AD) Motion, which accurately describe the relationships between force, velocity, and acceleration on a body.
    [Show full text]
  • Classical Mechanics
    Classical Mechanics Hyoungsoon Choi Spring, 2014 Contents 1 Introduction4 1.1 Kinematics and Kinetics . .5 1.2 Kinematics: Watching Wallace and Gromit ............6 1.3 Inertia and Inertial Frame . .8 2 Newton's Laws of Motion 10 2.1 The First Law: The Law of Inertia . 10 2.2 The Second Law: The Equation of Motion . 11 2.3 The Third Law: The Law of Action and Reaction . 12 3 Laws of Conservation 14 3.1 Conservation of Momentum . 14 3.2 Conservation of Angular Momentum . 15 3.3 Conservation of Energy . 17 3.3.1 Kinetic energy . 17 3.3.2 Potential energy . 18 3.3.3 Mechanical energy conservation . 19 4 Solving Equation of Motions 20 4.1 Force-Free Motion . 21 4.2 Constant Force Motion . 22 4.2.1 Constant force motion in one dimension . 22 4.2.2 Constant force motion in two dimensions . 23 4.3 Varying Force Motion . 25 4.3.1 Drag force . 25 4.3.2 Harmonic oscillator . 29 5 Lagrangian Mechanics 30 5.1 Configuration Space . 30 5.2 Lagrangian Equations of Motion . 32 5.3 Generalized Coordinates . 34 5.4 Lagrangian Mechanics . 36 5.5 D'Alembert's Principle . 37 5.6 Conjugate Variables . 39 1 CONTENTS 2 6 Hamiltonian Mechanics 40 6.1 Legendre Transformation: From Lagrangian to Hamiltonian . 40 6.2 Hamilton's Equations . 41 6.3 Configuration Space and Phase Space . 43 6.4 Hamiltonian and Energy . 45 7 Central Force Motion 47 7.1 Conservation Laws in Central Force Field . 47 7.2 The Path Equation .
    [Show full text]
  • Engineering Physics I Syllabus COURSE IDENTIFICATION Course
    Engineering Physics I Syllabus COURSE IDENTIFICATION Course Prefix/Number PHYS 104 Course Title Engineering Physics I Division Applied Science Division Program Physics Credit Hours 4 credit hours Revision Date Fall 2010 Assessment Goal per Outcome(s) 70% INSTRUCTION CLASSIFICATION Academic COURSE DESCRIPTION This course is the first semester of a calculus-based physics course primarily intended for engineering and science majors. Course work includes studying forces and motion, and the properties of matter and heat. Topics will include motion in one, two, and three dimensions, mechanical equilibrium, momentum, energy, rotational motion and dynamics, periodic motion, and conservation laws. The laboratory (taken concurrently) presents exercises that are designed to reinforce the concepts presented and discussed during the lectures. PREREQUISITES AND/OR CO-RECQUISITES MATH 150 Analytic Geometry and Calculus I The engineering student should also be proficient in algebra and trigonometry. Concurrent with Phys. 140 Engineering Physics I Laboratory COURSE TEXT *The official list of textbooks and materials for this course are found on Inside NC. • COLLEGE PHYSICS, 2nd Ed. By Giambattista, Richardson, and Richardson, McGraw-Hill, 2007. • Additionally, the student must have a scientific calculator with trigonometric functions. COURSE OUTCOMES • To understand and be able to apply the principles of classical Newtonian mechanics. • To effectively communicate classical mechanics concepts and solutions to problems, both in written English and through mathematics. • To be able to apply critical thinking and problem solving skills in the application of classical mechanics. To demonstrate successfully accomplishing the course outcomes, the student should be able to: 1) Demonstrate knowledge of physical concepts by their application in problem solving.
    [Show full text]
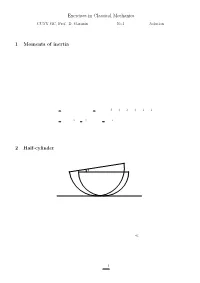
  • Exercises in Classical Mechanics 1 Moments of Inertia 2 Half-Cylinder
    Exercises in Classical Mechanics CUNY GC, Prof. D. Garanin No.1 Solution ||||||||||||||||||||||||||||||||||||||||| 1 Moments of inertia (5 points) Calculate tensors of inertia with respect to the principal axes of the following bodies: a) Hollow sphere of mass M and radius R: b) Cone of the height h and radius of the base R; both with respect to the apex and to the center of mass. c) Body of a box shape with sides a; b; and c: Solution: a) By symmetry for the sphere I®¯ = I±®¯: (1) One can ¯nd I easily noticing that for the hollow sphere is 1 1 X ³ ´ I = (I + I + I ) = m y2 + z2 + z2 + x2 + x2 + y2 3 xx yy zz 3 i i i i i i i i 2 X 2 X 2 = m r2 = R2 m = MR2: (2) 3 i i 3 i 3 i i b) and c): Standard solutions 2 Half-cylinder ϕ (10 points) Consider a half-cylinder of mass M and radius R on a horizontal plane. a) Find the position of its center of mass (CM) and the moment of inertia with respect to CM. b) Write down the Lagrange function in terms of the angle ' (see Fig.) c) Find the frequency of cylinder's oscillations in the linear regime, ' ¿ 1. Solution: (a) First we ¯nd the distance a between the CM and the geometrical center of the cylinder. With σ being the density for the cross-sectional surface, so that ¼R2 M = σ ; (3) 2 1 one obtains Z Z 2 2σ R p σ R q a = dx x R2 ¡ x2 = dy R2 ¡ y M 0 M 0 ¯ 2 ³ ´3=2¯R σ 2 2 ¯ σ 2 3 4 = ¡ R ¡ y ¯ = R = R: (4) M 3 0 M 3 3¼ The moment of inertia of the half-cylinder with respect to the geometrical center is the same as that of the cylinder, 1 I0 = MR2: (5) 2 The moment of inertia with respect to the CM I can be found from the relation I0 = I + Ma2 (6) that yields " µ ¶ # " # 1 4 2 1 32 I = I0 ¡ Ma2 = MR2 ¡ = MR2 1 ¡ ' 0:3199MR2: (7) 2 3¼ 2 (3¼)2 (b) The Lagrange function L is given by L('; '_ ) = T ('; '_ ) ¡ U('): (8) The potential energy U of the half-cylinder is due to the elevation of its CM resulting from the deviation of ' from zero.
    [Show full text]
  • Post-Newtonian Approximation
    Post-Newtonian gravity and gravitational-wave astronomy Polarization waveforms in the SSB reference frame Relativistic binary systems Effective one-body formalism Post-Newtonian Approximation Piotr Jaranowski Faculty of Physcis, University of Bia lystok,Poland 01.07.2013 P. Jaranowski School of Gravitational Waves, 01{05.07.2013, Warsaw Post-Newtonian gravity and gravitational-wave astronomy Polarization waveforms in the SSB reference frame Relativistic binary systems Effective one-body formalism 1 Post-Newtonian gravity and gravitational-wave astronomy 2 Polarization waveforms in the SSB reference frame 3 Relativistic binary systems Leading-order waveforms (Newtonian binary dynamics) Leading-order waveforms without radiation-reaction effects Leading-order waveforms with radiation-reaction effects Post-Newtonian corrections Post-Newtonian spin-dependent effects 4 Effective one-body formalism EOB-improved 3PN-accurate Hamiltonian Usage of Pad´eapproximants EOB flexibility parameters P. Jaranowski School of Gravitational Waves, 01{05.07.2013, Warsaw Post-Newtonian gravity and gravitational-wave astronomy Polarization waveforms in the SSB reference frame Relativistic binary systems Effective one-body formalism 1 Post-Newtonian gravity and gravitational-wave astronomy 2 Polarization waveforms in the SSB reference frame 3 Relativistic binary systems Leading-order waveforms (Newtonian binary dynamics) Leading-order waveforms without radiation-reaction effects Leading-order waveforms with radiation-reaction effects Post-Newtonian corrections Post-Newtonian spin-dependent effects 4 Effective one-body formalism EOB-improved 3PN-accurate Hamiltonian Usage of Pad´eapproximants EOB flexibility parameters P. Jaranowski School of Gravitational Waves, 01{05.07.2013, Warsaw Relativistic binary systems exist in nature, they comprise compact objects: neutron stars or black holes. These systems emit gravitational waves, which experimenters try to detect within the LIGO/VIRGO/GEO600 projects.
    [Show full text]
  • Euler and the Dynamics of Rigid Bodies Sebastià Xambó Descamps
    Euler and the dynamics of rigid bodies Sebastià Xambó Descamps Abstract. After presenting in contemporary terms an outline of the kinematics and dynamics of systems of particles, with emphasis in the kinematics and dynamics of rigid bodies, we will consider briefly the main points of the historical unfolding that produced this understanding and, in particular, the decisive role played by Euler. In our presentation the main role is not played by inertial (or Galilean) observers, but rather by observers that are allowed to move in an arbitrary (smooth, non-relativistic) way. 0. Notations and conventions The material in sections 0-6 of this paper is an adaptation of parts of the Mechanics chapter of XAMBÓ-2007. The mathematical language used is rather standard. The read- er will need a basic knowledge of linear algebra, of Euclidean geometry (see, for exam- ple, XAMBÓ-2001) and of basic calculus. 0.1. If we select an origin in Euclidean 3-space , each point can be specified by a vector , where is the Euclidean vector space associated with . This sets up a one-to-one correspondence between points and vectors . The inverse map is usually denoted . Usually we will speak of “the point ”, instead of “the point ”, implying that some point has been chosen as an origin. Only when conditions on this origin become re- levant will we be more specific. From now on, as it is fitting to a mechanics context, any origin considered will be called an observer. When points are assumed to be moving with time, their movement will be assumed to be smooth.
    [Show full text]
  • Kinematics, Kinetics, Dynamics, Inertia Kinematics Is a Branch of Classical
    Course: PGPathshala-Biophysics Paper 1:Foundations of Bio-Physics Module 22: Kinematics, kinetics, dynamics, inertia Kinematics is a branch of classical mechanics in physics in which one learns about the properties of motion such as position, velocity, acceleration, etc. of bodies or particles without considering the causes or the driving forces behindthem. Since in kinematics, we are interested in study of pure motion only, we generally ignore the dimensions, shapes or sizes of objects under study and hence treat them like point objects. On the other hand, kinetics deals with physics of the states of the system, causes of motion or the driving forces and reactions of the system. In a particular state, namely, the equilibrium state of the system under study, the systems can either be at rest or moving with a time-dependent velocity. The kinetics of the prior, i.e., of a system at rest is studied in statics. Similarly, the kinetics of the later, i.e., of a body moving with a velocity is called dynamics. Introduction Classical mechanics describes the area of physics most familiar to us that of the motion of macroscopic objects, from football to planets and car race to falling from space. NASCAR engineers are great fanatics of this branch of physics because they have to determine performance of cars before races. Geologists use kinematics, a subarea of classical mechanics, to study ‘tectonic-plate’ motion. Even medical researchers require this physics to map the blood flow through a patient when diagnosing partially closed artery. And so on. These are just a few of the examples which are more than enough to tell us about the importance of the science of motion.
    [Show full text]
  • New Rotational Dynamics- Inertia-Torque Principle and the Force Moment the Character of Statics Guagsan Yu* Harbin Macro, Dynamics Institute, P
    Computa & tio d n ie a l l p M Yu, J Appl Computat Math 2015, 4:3 p a Journal of A t h f e o m l DOI: 10.4172/2168-9679.1000222 a a n t r ISSN: 2168-9679i c u s o J Applied & Computational Mathematics Research Article Open Access New Rotational Dynamics- Inertia-Torque Principle and the Force Moment the Character of Statics GuagSan Yu* Harbin Macro, Dynamics Institute, P. R. China Abstract Textual point of view, generate in a series of rotational dynamics experiment. Initial research, is wish find a method overcome the momentum conservation. But further study, again detected inside the classical mechanics, the error of the principle of force moment. Then a series of, momentous the error of inside classical theory, all discover come out. The momentum conservation law is wrong; the newton third law is wrong; the energy conservation law is also can surpass. After redress these error, the new theory namely perforce bring. This will involve the classical physics and mechanics the foundation fraction, textbooks of physics foundation part should proceed the grand modification. Keywords: Rigid body; Inertia torque; Centroid moment; Centroid occurrence change? The Inertia-torque, namely, such as Figure 3 the arm; Statics; Static force; Dynamics; Conservation law show, the particle m (the m is also its mass) is a r 1 to O the slewing radius, so it the Inertia-torque is: Introduction I = m.r1 (1.1) Textual argumentation is to bases on the several simple physics experiment, these experiments pass two videos the document to The Inertia-torque is similar with moment of force, to the same of proceed to demonstrate.
    [Show full text]
  • A Short History of Physics (Pdf)
    A Short History of Physics Bernd A. Berg Florida State University PHY 1090 FSU August 28, 2012. References: Most of the following is copied from Wikepedia. Bernd Berg () History Physics FSU August 28, 2012. 1 / 25 Introduction Philosophy and Religion aim at Fundamental Truths. It is my believe that the secured part of this is in Physics. This happend by Trial and Error over more than 2,500 years and became systematic Theory and Observation only in the last 500 years. This talk collects important events of this time period and attaches them to the names of some people. I can only give an inadequate presentation of the complex process of scientific progress. The hope is that the flavor get over. Bernd Berg () History Physics FSU August 28, 2012. 2 / 25 Physics From Acient Greek: \Nature". Broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves. The universe is commonly defined as the totality of everything that exists or is known to exist. In many ways, physics stems from acient greek philosophy and was known as \natural philosophy" until the late 18th century. Bernd Berg () History Physics FSU August 28, 2012. 3 / 25 Ancient Physics: Remarkable people and ideas. Pythagoras (ca. 570{490 BC): a2 + b2 = c2 for rectangular triangle: Leucippus (early 5th century BC) opposed the idea of direct devine intervention in the universe. He and his student Democritus were the first to develop a theory of atomism. Plato (424/424{348/347) is said that to have disliked Democritus so much, that he wished his books burned.
    [Show full text]
  • NEWTON's FIRST LAW of MOTION the Law of INERTIA
    NEWTON’S FIRST LAW OF MOTION The law of INERTIA INERTIA - describes how much an object tries to resist a change in motion (resist a force) inertia increases with mass INERTIA EXAMPLES Ex- takes more force to stop a bowling ball than a basket ball going the same speed (bowling ball tries more to keep going at a constant speed- resists stopping) Ex- it takes more force to lift a full backpack than an empty one (full backpack tries to stay still more- resists moving ; it has more inertia) What the law of inertia says…. AKA Newton’s First Law of Motion An object at rest, stays at rest Because the net force is zero! Forces are balanced (equal & opposite) …an object in motion, stays in motion Motion means going at a constant speed & in a straight line The net force is zero on this object too! NO ACCELERATION! …unless acted upon by a net force. Only when this happens will you get acceleration! (speed or direction changes) Forces are unbalanced now- not all equal and opposite there is a net force> 0N! You have overcome the object’s inertia! How does a traveling object move once all the forces on it are balanced? at a constant speed in a straight line Why don’t things just move at a constant speed in a straight line forever then on Earth? FRICTION! Opposes the motion & slows things down or GRAVITY if motion is in up/down direction These make the forces unbalanced on the object & cause acceleration We can’t get away from those forces on Earth! (we can encounter some situations where they are negligible though!) HOW can you make a Bowling
    [Show full text]
  • RELATIVISTIC GRAVITY and the ORIGIN of INERTIA and INERTIAL MASS K Tsarouchas
    RELATIVISTIC GRAVITY AND THE ORIGIN OF INERTIA AND INERTIAL MASS K Tsarouchas To cite this version: K Tsarouchas. RELATIVISTIC GRAVITY AND THE ORIGIN OF INERTIA AND INERTIAL MASS. 2021. hal-01474982v5 HAL Id: hal-01474982 https://hal.archives-ouvertes.fr/hal-01474982v5 Preprint submitted on 3 Feb 2021 (v5), last revised 11 Jul 2021 (v6) HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Distributed under a Creative Commons Attribution| 4.0 International License Relativistic Gravity and the Origin of Inertia and Inertial Mass K. I. Tsarouchas School of Mechanical Engineering National Technical University of Athens, Greece E-mail-1: [email protected] - E-mail-2: [email protected] Abstract If equilibrium is to be a frame-independent condition, it is necessary the gravitational force to have precisely the same transformation law as that of the Lorentz-force. Therefore, gravity should be described by a gravitomagnetic theory with equations which have the same mathematical form as those of the electromagnetic theory, with the gravitational mass as a Lorentz invariant. Using this gravitomagnetic theory, in order to ensure the relativity of all kinds of translatory motion, we accept the principle of covariance and the equivalence principle and thus we prove that, 1.
    [Show full text]