DOCSLIB.ORG

Two-Phase Auto-Piloted Synchronous Motors and Actuators

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Two-Phase Auto-Piloted Synchronous Motors and Actuators IMPERIAL COLLEGE OF SCIENCE AND TECHNOLOGY DEPARTMENT OF ELECTRICAL ENGINEERING TWO-PHASE AUTO-PILOTED SYNCHRONOUS MOTORS AND ACTUATORS it Thesis submitted for the degree of Doctor of Philosophy of the University of London. it by Amadeu Leao Santos Rodrigues, M.Sc. (D.I.C.) July 1983 The thesis is concerned with certain aspects of the design and per- formance of drives based on variable speed synchronous motors fed from variable frequency sources, controlled by means of rotor-position sensors. This auto-piloted or self-synchronised form of control enables the machine to operate either with an adjustable load angle or an adjustable torque angle depending on whether a voltage or a current source feed is used. D.c. machine-type characteristics can thus be obtained from the system. The thesis commences with an outline of some fundamental design aspects and a summary of torque production mechanisms in electrical machines. The influence of configuration and physical size on machine performance is discussed and the advantages of the use for servo applic- ations of direct-drive as opposed to step-down transmissions are explained. Developments in permanent magnet materials have opened the way to permanent magnet motors of improved performance, and a brief review of the properties of the various materials presently available is given. A finite-difference method using magnetic scalar potential for calculating the magnetic field of permanent magnets in the presence of iron cores and macroscopic currents is described. A comparison with the load line method is made for some typical cases. Analogies between the mechanical commutator of a d.c. machine and the electronic commutator of the system studied are drawn and a theory valid for damper-less motors operating under both steady and dynamic conditions is presented. The design, manufacture and testing of a 1000 lb.ft, limited motion, rare-earth permanent-magnet-excited rotary actuator, begun in an earlier project, is described. Computer solutions for the numerical calculation of air gap flux density distribution, air gap inductance and demagnetisation current limit are given and correlated with test results. D.c. disc motors with printed circuit armatures are now widely used in servo applications. The design, construction and testing of a per- manent-magnet-excited, rotating-armature, auto-piloted synchronous disc motor is described. Two types of rotor construction were investigated. Finally, experimental results serve to supplement a theoretical com- parison between disc and equivalent drum motors. Both coil excitation and permanent magnet field excitation are considered. ACKNOWLEDGEMENTS The work described in this thesis was carried out under the supervision of Dr H.Bolton, B.Sc.(Eng.), Ph.D., Reader in Electrical Machines at the Department of Electrical Engineering, Imperial College of Science and Tech- nology, London. For the invaluable help, advice, constant encouragement and stimulating discussions during the course of this work, the author would like to express his extreme gratitude to his supervisor. The bulk of the manufacturing work of the prototypes and test rigs was carried out in the Electrical Engineering Workshop at Imperial College, under the supervision of Mr. R. Moore to whom, along with his staff, the author is grateful. Thanks are also due to Mr. R.B. Owen for his practical assistance and advice during the work. Considerable assistance was received from Dr. D. Pedder and Mr N. Mallinson on problems associated with the electronic portions. The author is deeply indebted to the "Universidade Nova de Lisboa" for all the facilities provided and to the "Instituto Nacional de Investigacao Cientffica" for generous financial support received during his studies in England, without which this work would not have been possible. Thanks are finally due to many colleagues and friends at Imperial College who have helped to make the research enjoyable. CONTENTS Page ABSTRACT ii ACKNOWLEDGEMENTS iv CONTENTS v INTRODUCTION 1 CHAPTER 1: SOME FUNDAMENTAL ASPECTS OF ELECTRICAL MACHINES 7 1.1 - GENERALITIES 7 1.2 - ELECTROMAGNETIC TORQUE IN INDUCTIVELY COUPLED CIRCUITS 7 1.2.1 - Particular cases 9 1.3 - MAGNETIC AND ELECTROMAGNETIC MACHINES 14 1.3.1 - Electromagnetic machines 14 1.3.2 - Magnetic machines 15 1.4 - ELECTRICAL MACHINES TOPOLOGY 18 1.5 - TORQUE EXPRESSION FOR A TWO-PHASE MULTI-POLE SYNCHRONOUS MOTOR 20 1.6 - POLE PROFILE FOR A SINUSOIDAL AIR GAP FLUX DENSITY DISTRIBUTION 30 1.7 - SPECIFIC TANGENTIAL FORCE DEVELOPED BY AN ELECTROMAGNETIC MACHINE 32 1.8 - VARIATION OF STATOR INSIDE RADIUS WITH STATOR OUTSIDE RADIUS 34 vi Page 1.9 - DYNAMIC FACTORS OF A MOTOR 36 1.9.1 - Optimal gear ratio 37 1.9.2 - Variation of dynamic factors with motor proportions 39 1.9.3 - Comparison between a direct and an optimal gearing drive 41 1.10 - HYDRAULIC MOTOR VERSUS ELECTRIC TORQUE MOTOR 45 1.11 - COMPARISON BETWEEN ARCUATE AND CYLINDRICAL CONFIGURATIONS 48 1.12 - COMPARISON BETWEEN DISC AND CYLINDRICAL CONFIGURATIONS 50 1.13 - EQUIVALENT CIRCUIT AND PHASOR DIAGRAM OF A SYNCHRONOUS MOTOR 55 1.14 - INDUCTANCE CALCULATION 57 1.14.1 - Expressions for leakage inductance 58 1.14.2- Air gap inductance of q coils linked 60 1.15 - STATOR FLUX DENSITY ON LOAD 67 CHAPTER 2: PERMANENT MAGNET FIELD ANALYSIS 73 2.1 - GENERALITIES 73 2.2 - FUNDAMENTAL PARAMETERS OF A PERMANENT MAGNET MATERIAL 74 2.2.1 - Intrinsic magnetisation or polarisation 75 2.2.2 - The various permeabilities 79 2.2.3 - The Energy Product 81 2.2.4 - The shape factor 84 2.3 - CLASSIFICATION OF PERMANENT MAGNET MATERIALS 84 2.4 - MAGNET ARRANGEMENT IN ROTATING ELECTRICAL MACHINES 88 2.5 - THE CALCULATION OF A PERMANENT MAGNET UNDER STATIC CONDITIONS 91 2.5.1 - Working point for the minimum volume of the magnet material 94 vn 2.5.2 - Leakage factor formulae for specific permanent magnet configurations 2.6 - THE CALCULATION OF A PERMANENT MAGNET UNDER DYNAMIC CONDITIONS 2.6.1 - Recoil constant energy contours 2.7 - COMPUTATION OF THE FIELD DISTRIBUTION IN A PERMANENT MAGNET MACHINE 2.7.1 - Modelling the magnetic field problem in permanent magnet devices 2.7.2 - Linear representation of demagnetisation characteristics 2.7.3 - Derivation of finite-difference equations for magneti scalar potential in polar coordinates 2.7.4 - Field solution at no-load 2.7.5 - Field solution on load 2.7.6 - Flux plot 2.7.7 - Derivation of finite-difference equations for magneti scalar potential in cylindrical coordinates 2.8 - COMPARISON OF LOAD LINE AND MESH ANALYSIS METHOD 2.8.1 - Calculation of the air gap flux density using the load-line method 2.8.2 - Calculation of the air gap flux density using the mesh analysis method 2.9 - MANUAL SOLUTION FOR THE MAXIMUM PERMISSIBLE STATOR CURRENT CALCULATION CHAPTER 3: AUTO-PILOTED SYNCHRONOUS MOTOR THEORY 3.1 - GENERALITIES 3.2 - MECHANICAL COMMUTATOR REPLACEMENT 3.3 - TRANSISTOR-SWITCHED TWO-PHASE SYNCHRONOUS MOTOR PRINCIPLE viii Page 3.4 - SINE WAVE OPERATION 157 3.5 - TYPES OF ROTOR POSITION SENSORS 159 3.6 - OVERALL SYNCHRO-RESOLVER SYSTEM 166 3.6.1 - Influence of the ratio w /m r c in synchro-resolver system 174 3.7 - ANALYSIS OF THE SYNCHRONOUS MOTOR WITH ROTOR POSITION CONTROL 177 3.7.1 - Steady-state theory of a synchronous motor operating at variable-frequency and fixed load angle 180 3.7.2 - Steady-state theory of a synchronous motor operating at variable-frequency and fixed torque angle 193 3.7.3 - Operating chart for a synchronous motor at variable frequency 203 3.8 - MOTOR RESPONSE TO A STEP INPUT SIGNAL 204 CHAPTER 4: LIMITED MOTION, ROTARY BRUSHLESS ACTUATOR 208 4.1 - GENERALITIES 208 4.2 - DESIGN OF ACTUATOR STATOR 209 4.3 - WINDING ARRANGEMENT 213 4.3.1 - Winding factor 214 4.4 - LEAKAGE INDUCTANCE CALCULATION 215 4.4.1 - Slot leakage inductance 215 4.4.2 - End-winding leakage inductance 218 4.5 - DESIGN OF ACTUATOR ROTOR 219 4.6 - AIR GAP FLUX DENSITY DISTRIBUTION ON NO LOAD 221 4.6.1 - Flux set up per tooth pitch by the B.P.R.E. magnet 222 4.7 - NORMAL FORCE SEEN BY THE SHAFT 225 4.8 - AIR GAP INDUCTANCE CALCULATION 228 4.9 - STATOR CURRENT LIMITATION 231 ix 4.9.1 - Current limit for starting saturation of the magnetic circuit 4.9.2 - Current limit for starting demagnetisation of the permanent magnets 4.10 - FUNDAMENTAL ELECTROMAGNETIC TORQUE 4.11 - PREDICTED RIPPLE TORQUE 4.12 - TEST RESULTS 4.12.1 - Static torque tests 4.12.2 - Stator winding inductance measurement 4.12.3 - Air gap flux density measurement 4.12.4 - Temperature-rise test 4.12.5 - Rotor inertia measurement 4.12.6 - Viscous damping coefficient measurement 4.13 - DESCRIPTION OF THE COMPLETE ACTUATOR SYSTEM 4.13.1 - Synchro-resolver characteristics 4.13.2 - Machine requirements for electronic supply matching 4.13.3 - Actuator dynamic behaviour 4.14 - POSITION CONTROLLER 4.14.1 - System response to a step input 4.14.2 - Effect of tachometer feedback 4.14.3 - System response with variable input 4.15 - NOVEL TACHOMETER CHAPTER 5: TWO-PHASE AUTO-PILOTED DISC SYNCHRONOUS MOTOR 5.1 - GENERALITIES 5.2 - MACHINE CONFIGURATION 5.2.1 - Wire-wound rotor construction 5.2.2 - Printed rotor layout 5.3 - AIR GAP FLUX DENSITY CALCULATION Page 5.4 - ARMATURE REACTION AND INDUCTANCE CALCULATION 300 5.5 - BACK E.M.F. AND TORQUE CONSTANT 301 5.5.1 - Torque constant evaluation 305 5.6 - TWO-PHASE INVERTER CIRCUITRY 306 5.7 - MACHINE OPERATION FROM A SINUSOIDAL SUPPLY 309 5.8 - TEST RIG FOR OBTAINING SPEED CHARACTERISTICS 313 5.8.1 - The speedometer 314 5.8.2 - The eddy-current brake 315 5.9 - TEST RESULTS 317 5.9.1 - Air gap flux density measurement 317
Load more

Recommended publications
  • Single-Phase Line Start Permanent Magnet Synchronous Motor with Skewed Stator*
    POWER ELECTRONICS AND DRIVES Vol. 1(36), No. 2, 2016 DOI: 10.5277/PED160212 SINGLE-PHASE LINE START PERMANENT MAGNET SYNCHRONOUS MOTOR WITH SKEWED STATOR* MACIEJ GWOŹDZIEWICZ, JAN ZAWILAK Wrocław University of Science and Technology, Wybrzeże Stanisława Wyspiańskiego 27, 50-370 Wrocław, Poland, e-mail: [email protected], [email protected] Abstract: The article deals with single-phase line start permanent magnet synchronous motor with skewed stator. Constructions of two physical motor models are presented. Results of the motors run- ning properties are analysed. Keywords: single-phase motor, permanent magnet, skew, vibration 1. INTRODUCTION Single-phase induction motors almost always have skewed rotors. It is a simple and effective solution in limitation of the motor vibration, noise and torque pulsation. In the case of line start permanent magnet synchronous motors skewed rotor is ex- tremely difficult to manufacture due to interior permanent magnets. Skewed stator is less complicated in comparison with skewed rotor [3], [4], [7], [8]. During many tests of single-phase line start permanent magnet synchronous motor physical models The authors noticed that vibration is one of the main drawbacks of these motors [1], [2]. It prompted them to construct and build a single-phase line start permanent magnet motor with skewed stator. 2. MOTOR CONSTRUCTION Two dimensional field-circuit models of the single-phase line start permanent magnet synchronous motor were applied in Maxwell software. The models are based on the mass production single-phase induction motor Seh 80-2B type: rated power Pn = 1.1 kW, rated voltage Un = 230 V, rated frequency fn = 50 Hz, number of pole * Manuscript received: September 7, 2016; accepted: December 7, 2016.
    [Show full text]
  • Chapter # 2 Cylindrical Synchronous Generator and Motor 1
    Benha University Electrical Engineering Department Faculty of Engineering at Shubra Electric Machines II Chapter # 2 Cylindrical Synchronous Generator and Motor 1. Introduction Synchronous machines are named by this name as their speed is directly related to the line frequency. Synchronous machines may be operated either as motor or generator. Synchronous generators are called alternators. Synchronous motors are used mainly for power factor correction when operate at no load. Synchronous machines are usually constructed with stationary stator (armature) windings that carrying the current and rotating rotor (field) winding that create the magnetic flux. This flux is produced by DC current from a separate source (e.g. DC shunt generator). 2. Types of Synchronous Generators The type of synchronous generators depends on the prime mover type as: a) Steam turbines: synchronous generators that driven by steam turbine are high speed machines and known as turbo alternators. The maximum rotor speed is 3600 rpm corresponding 60 Hz and two poles. b) Hydraulic turbines: synchronous generators that driven by water turbine are with speed varies from 50 to 500 rpm. The type of turbine to be used depends on the water head. For water head of 400m, Pelton wheel turbines are used. But for water head up to 350 m, Francis Turbines are used. For water head up to 50 m, Kaplan Turbines are used. 1 Chapter #2 Cylindrical Synchronous Machines Dr. Ahmed Mustafa Hussein Benha University Electrical Engineering Department Faculty of Engineering at Shubra Electric Machines II c) Diesel Engines: they are used as prime movers for synchronous generator of small ratings. For the type a) and c) the rotor shape is cylindrical as shown in Fig.
    [Show full text]
  • Hybrid Synchronous Motor Electromagnetic Torque Research
    MATEC Web of Conferences 19, 01026 (2014) DOI: 10.1051/matecconf/201419 01 026 C Owned by the authors, published by EDP Sciences, 2014 Hybrid synchronous motor electromagnetic torque research Elena E. Suvorkovaa, Lev K. Burulko National Research Tomsk Polytechnic University, 634050 Tomsk, Russia Abstract. Electromagnetic field distribution models in reluctance and permanent magnet parts were made by means of Elcut. Dependences of electromagnetic torque on torque angle were obtained. 1. Introduction Present-day position is inextricably connected with developing process in all components of electric drive: electrical machines, power semiconductors and converters on its base. One of the main electric motors development directions is expanding special motors’ construction range for applying in modern competitive object-orientated systems. Electric machines prospects of promotion lead to its non-traditional usage such as hybrid synchronous motor (HSM). HSM main principles of operation make it possible to use as executive engine in a number of production plants, such as artificial fiber production [1]. Electric drive projecting involves verification and regulation method choice which are determined by main electric machine characteristics. Thus main goals of this paper are hybrid synchronous motor air-gap magnetic field research and electromagnetic torque main parts determination. 2. Problem statement HSM is a machine with stator created on basis of serial asynchronous motor and rotor consisting on two parts. The main rotor part is a reluctance machine which is 70% of active rotor length [2], the other is synchronous permanent-magnet machine which is 30% [1]. Power is developed by reluctance machine as the cheapest and simple in design, and energy of constant magnets poles is used for increasing power and improving operational characteristics.
    [Show full text]
  • Rita MBAYED Contribution to the Control of the Hybrid Excitation
    Année 2012 UNIVERSITE DE CERGY PONTOISE THESE Présentée pour obtenir le grade de DOCTEUR DE L’UNIVERSITE DE CERGY PONTOISE Ecole doctorale: Sciences et Ingénierie Spécialité: Génie Electrique Soutenance publique prévue le 12 Décembre 2012 Par Rita MBAYED Contribution to the Control of the Hybrid Excitation Synchronous Machine for Embedded Applications JURY Rapporteurs : Prof. Gérard CHAMPENOIS Université de Poitiers Prof. Eric SEMAIL Ecole Nationale d'Arts et Métiers ParisTech Examinateurs : Prof. Francis LABRIQUE Université Catholique de Louvain Prof. Mohamed GABSI Ecole Normale Supérieure Cachan Dr. Vincent LANFRANCHI Université de Technologie de Compiègne Directeur de thèse : Prof. Eric MONMASSON Université de Cergy Pontoise Co-directeurs : Prof. GeorgesSALLOUM Université Libanaise Dr. Lionel VIDO Université de Cergy Pontoise Laboratoire SATIE - UCP/UMR 8029, 1 rue d’Eragny, 95031 Neuville sur Oise France The secret is comprised in three words: Work, finish, publish. Michael Faraday Ere many generations pass, our machinery will be driven by a power obtainable at any point of the universe. This idea is not novel. Men have been led to it long ago by instinct or reason; it has been expressed in many ways, and in many places, in the history of old and new. We find it in the delightful myth of Antheus, who derives power from the earth; we find it among the subtle speculations of one of your splendid mathematicians and in many hints and statements of thinkers of the present time. Throughout space there is energy. Is this energy static or kinetic? If static our hopes are in vain; if kinetic - and this we know it is, for certain - then it is a mere question of time when men will succeed in attaching their machinery to the very wheelwork of nature.
    [Show full text]
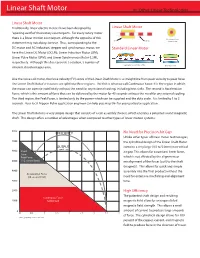
  • Linear Shaft Motor Vs
    Linear Shaft Motor vs. Other Linear Technologies Linear Shaft Motor Traditionally, linear electric motors have been designed by Linear Shaft Motor “opening out flat” their rotary counterparts. For every rotary motor there is a linear motion counterpart, although the opposite of this No influence from Coil Magnets statement may not always be true. Thus, corresponding to the change in gap DC motor and AC induction, stepper and synchronous motor, we Standard Linear Motor have the Linear DC Motor (DCLM), Linear Induction Motor (LIM), Linear Pulse Motor (LPM), and Linear Synchronous Motor (LSM), respectively. Although this does provide a solution, a number of Cogging by concentration of flux inherent disadvantages arise. Absorption force Like the voice coil motor, the force velocity (FV) curve of the Linear Shaft Motor is a straight line from peak velocity to peak force. The Linear Shaft Motor’s FV curves are split into three regions. The first is what we call Continuous Force. It is the region in which the motor can operate indefinitely without the need for any external cooling, including heat sinks. The second is Acceleration Force, which is the amount of force that can be delivered by the motor for 40 seconds without the need for any external cooling. The third region, the Peak Force, is limited only by the power which can be supplied and the duty cycle. It is limited to 1 to 2 seconds. Your local Nippon Pulse application engineer can help you map this for your particular application. The Linear Shaft Motor is a very simple design that consists of a coil assembly (forcer), which encircles a patented round magnetic shaft.
    [Show full text]
  • Apermanent Magnet Synchronous Motor for an Electric Vehicle
    TRITA-ETS-2004-04 ISSN 1650-674x ISRN KTH/R 0404-SE ISBN 91-7283-803-5 A PERMANENT MAGNET SYNCHRONOUS MOTOR FOR AN ELECTRIC VEHICLE - DESIGN ANALYSIS Yung-kang Chin Stockholm 2004 ELECTRICAL MACHINES AND POWER ELECTRONICS DEPARTMENT OF ELECTRICAL ENGINEERING ROYAL INSTITUTE OF TECHNOLOGY SWEDEN Submitted to the School of Computer Science, Electrical Engineering and Engineering Physics, KTH, in partial fulfilment of the requirements for the degree of Technical Licentiate. Copyright © Yung-kang Chin, Sweden, 2004 Printed in Sweden Universitetsservice US AB TRITA-ETS-2004-04 ISSN 1650-674x ISRN KTH/R 0404-SE ISBN 91-7283-803-5 PPrreeffaaccee This technical licentiate thesis deals with the design analysis of a permanent magnet synchronous motor for an electric vehicle. A thesis is a report that conveys the used theoretical approach and the experimental results on a specific problem in a specific area. A thesis could also develop a purely theoretical approach to a topic. It is my aim as the author to present these findings and theoretical approaches clearly and effectively with this concise report. Never Say Never! This is the phrase I have always referred to and it even appears on my screensaver. When I started my doctoral study at KTH, my plan was to write my doctoral dissertation directly without taking the licentiate examination. Well, as I am now writing the preface of my licentiate thesis, my thought has obviously changed through out the duration of the project work. A good friend of mine, who has a PhD degree in Physics himself, once told me that working on a doctoral degree is just like walking through a long dark tunnel.
    [Show full text]
  • What Is a Synchronous AC Motor? Hysteresis and Reluctance Type Designs
    A TECHNICAL PAPER FROM BODINE ELECTRIC COMPANY What Is a Synchronous AC Motor? Hysteresis and Reluctance Type Designs Introduction The difference between the speed of the rotating magnetic field of an induction motor (which is always synchronous) and the speed of the rotor is known as “slip.” When the rotor design enables it to “lock into step” with the field, the slip is reduced to zero and the motor is said to run at synchronous speed. Upon reaching the running mode, synchronous motors operate at constant speed -- the speed being dependent on the frequency of the power supply. This constant speed feature makes fixed-speed AC synchronous motors an ideal, low-cost solution for timing and other applications requiring a constant speed output, and without the need for a motor speed control. Design and Operation There are two common types of small synchronous AC induction motors, classified according to the type of rotor used: AMPS RPMs Pull In Pull Out HP a) hysteresis synchronous motors. 2.0 2000 0.10 b) reluctance synchronous motors 1.6 1600 0.08 1. Hysteresis-type AC synchronous motors: Unlike squirrel- cage rotor AC induction motors, this motor type develops 1.2 1200 0.06 torque because of the magnetic hysteresis loss induced in its permanent magnet alloy rotor core. Although the stator 0.8 800 0.04 in a hysteresis synchronous design is wound much like that FULL LOAD of the conventional squirrel cage motor, its rotor is made of 0.4 400 0.02 a heat-treated cast permanent magnet alloy cylinder (with a nonmagnetic support) securely mounted to the shaft.
    [Show full text]
  • BASIC CONCEPTS of MODELING 3 Phase Synchronous Machine With
    UNIT I - BASIC CONCEPTS OF MODELING 3 phase synchronous machine with and without damper bars and 3 - phase induction machine Introduction: It was shown in an earlier chapter that an alternator driven at a constant speed produces an alternating voltage at a fixed frequency dependent on the number of poles in the machine. A machine designed to be connected to the supply and run at synchronous speed is referred to as a synchronous machine. The description applies to both motors and generators. A synchronous condenser is a special application of a synchronous motor. While the synchronous motor has only one generally used name, the synchronous generator is on occasion referred to as an alternator or as an a.c. generator. The term alternator has been used in previous chapters and will be used in this chapter but it should be remembered that other terms are in use. In general, the principles of construction and operation are similar for both alternators and generators, just as there were basic similarities between d.c. motors and generators. While alternators were once seldom seen outside power houses and whole communities were supplied from a central source, there is now an expanding market for smaller sized alternators suitable for the provision of power for portable tools. Today, with the growth in computer control, there is a further need for standby generating plant to ensure a continuity of supply to prevent a loss of data from computer memories. So much information is being stored in computers today that even brief interruptions to the power supplies can have serious consequences on the accuracy and extent of information stored.
    [Show full text]
  • Dynamics Induced in Microparticles by Electromagnetic Fields
    DYNAMICS INDUCED IN MICROPARTICLES BY ELECTROMAGNETIC FIELDS A conceptual introduction to nanoelectromechanical systems Patricio Robles Escuela de Ingeniería Eléctrica, Pontificia Universidad Católica de Valparaíso, Chile Roberto Rojas Departamento de Física, Universidad Técnica Federico Santa María, Valparaíso, Chile Italo Chiarella Escuela de Ingeniería Eléctrica, Pontificia Universidad Católica de Valparaíso, Chile 1 PREFACE This is a review addressed to undergraduate students of electrical engineering and physics careers, and our aim is to present a pedagogical integration of some knowledge acquired in electromagnetism and electromechanical energy conversion courses, and to show how they can be used in actual technology applications, in particular for microscopic and nanoscopic systems. In general, the contents of electromagnetic courses looks rather abstract to students at an intermediate level of the electrical engineering career and its applications are hard to be appreciated by them. The course of electromechanical energy conversion provides to the students a good link with processes of electrical engineering but in our opinion it is necessary a book containing a better integration and correlation of topics learned in these courses, such as energy and momentum transfer between electromagnetic fields and movile devices, at a macroscopic and at a microscopic level. At a macroscopic scale, in general a good integration results in these courses for understanding how by means of variation in the energy stored in the magnetic field and interaction between rotating magnetic fields it is possible to produce mechanical or electric power for the operation of motors or generators, respectively. In general the programs of these courses give less emphasis on similar processes that are possible with the energy stored in the electric field as is the case, for example, of capacitors with movile plates or the interaction between electric polarized objects with rotating electric fields.
    [Show full text]
  • 5Cfefcfd1682f70bb4a20064c6b7
    Hindawi Mathematical Problems in Engineering Volume 2019, Article ID 1728768, 9 pages https://doi.org/10.1155/2019/1728768 Research Article Nonlinear Compound Control for Nonsinusoidal Vibration of the Mold Driven by Servo Motor with Variable Speed Qiang Li ,1 Yi-ming Fang ,1,2 Jian-xiong Li ,1 and Zhuang Ma1 1Key Lab of Industrial Computer Control Engineering of Hebei Province, Yanshan University, Qinhuangdao, Hebei Province 066004, China 2National Engineering Research Center for Equipment and Technology of Cold Strip Rolling, Qinhuangdao, Hebei Province 066004, China Correspondence should be addressed to Yi-ming Fang; [email protected] Received 24 April 2019; Revised 3 September 2019; Accepted 10 September 2019; Published 22 October 2019 Academic Editor: Francesc Pozo Copyright © 2019 Qiang Li et al. ,is is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In this paper, a fuzzy PI control method based on nonlinear feedforward compensation is proposed for the nonsinusoidal vibration system of mold driven by servo motor, rotated in single direction with variable speed. During controller design, there are mainly two issues to consider: (i) nonlinear relationship (approximate periodic function) between mold displacement and servo motor speed and (ii) uncertainties caused by backlash due to motor variable speed. So, firstly, the relationship between mold displacement and motor rotation speed is built directly based on the rotation vector method. ,en, an observer is designed to estimate the uncertainties and feedforward compensation. Secondly, as the motor rotates in single direction with variable speed, a fuzzy control with bidirectional parameter adjustment is adopted to improve rapidity and stability based on the traditional PI method.
    [Show full text]
  • Categorical Quantum Dynamics
    Categorical Quantum Dynamics Stefano Gogioso Trinity College University of Oxford arXiv:1709.09772v1 [quant-ph] 28 Sep 2017 A thesis submitted for the degree of Doctor of Philosophy Michaelmas 2016 Per Aspera Ad Astra Contents 1 Introduction 1 1.1 Summary of this work . .1 1.2 Background literature . .2 1.2.1 Categorical Quantum Mechanics . .2 1.2.2 Dagger compact structure . .3 1.2.3 Some application of CQM . .3 1.2.4 The ZX calculus . .4 1.2.5 Applications of strong complementarity . .4 1.3 Brief synopsis of this work . .6 1.3.1 A primer of CQM . .6 1.3.2 Coherent dynamics and symmetries . .6 1.3.3 Strong complementarity in quantum algorithms . .7 2 Categorical Quantum Mechanics 8 2.1 Symmetric monoidal categories . .8 2.1.1 Objects as physical systems . .8 2.1.2 Sequential composition of processes . .8 2.1.3 Parallel composition of processes . .9 2.1.4 States, effects and scalars . 11 2.1.5 Examples of symmetric monoidal categories . 12 2.2 Dagger-compact categories . 14 2.2.1 Dagger, isometries and unitaries . 14 2.2.2 Dagger compact structure . 15 2.2.3 Examples of dagger compact categories . 17 2.2.4 The matrix algebra . 19 2.3 Environments, causality and purification . 19 2.3.1 Environment structures . 19 2.3.2 Discarding maps in categories of matrices . 20 i 2.3.3 The CPM construction . 21 2.3.4 Purification . 24 2.4 Coherent data manipulation . 26 2.4.1 Dagger Frobenius algebras . 26 2.4.2 Quantum observables .
    [Show full text]
  • Probabilistic Methodology and Techniques for Artefact Conception and Development
    INSTITUTNATIONALDERECHERCHEENINFORMATIQUEETENAUTOMATIQUE Survey: Probabilistic Methodology and Techniques for Artefact Conception and Development Pierre Bessière & the BIBA - INRIA Research Group1 - Projet CYBERMOVE No4730 Février2003 THEM` E3 apport de recherche ISRN INRIA/RR--4730--FR+ENG ISSN 0249-6399 Survey: Probabilistic Methodology and Techniques for Artefact Conception and Development Pierre Bessière & the BIBA - INRIA Research Group1 Projet CYBERMOVE Thème 3 : Interaction homme-machine, images, données, connaissances [email protected] Rapport de recherche n°4730 - février 2003 Abstract: The purpose of this paper is to make a state of the art on probabilistic methodology and tech- niques for artefact conception and development. It is the 8th deliverable of the BIBA (Bayesian Inspired Brain and Artefacts) project. We first present the incompletness problem as the central diffi- culty that both living creatures and artefacts have to face: how can they perceive, infer, decide and act efficiently with incomplete and uncertain knowledge?. We then introduce a generic probabilistic formalism called Bayesian Programming. This formalism is then used to review the main probabilistic methodology and techniques. This review is organized in 3 parts: first the probabilistic models from Bayesian networks to Kalman filters and from sensor fusion to CAD systems, second the inference techniques and finally the learning and model acquisition and comparison methodologies. We conclude with the perspectives of the BIBA project as they rise from this state of the art. Keywords: Bayesian programming, Bayesian modelling, Bayesian reasoning, Bayesian learning, Bayesian networks 1. JUAN-MANUEL AHUACTZIN, OLIVIER AYCARD, DAVID BELLOT, FRANCIS COLAS, CHRISTOPHE COUÉ, JULIEN DIARD, RUBEN GARCIA, CARLA KOIKE, OLIVIER LEBEL- TEL, RONAN LEHY, OLIVIER MALRAIT, EMMANUEL MAZER, KAMEL MEKHNACHA, CÉDRIC PRADALIER, ANNE SPALANZANI 2 Bessière et al.
    [Show full text]