DOCSLIB.ORG

No. 40. the System of Lunar Craters, Quadrant Ii Alice P

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
No. 40. the System of Lunar Craters, Quadrant Ii Alice P NO. 40. THE SYSTEM OF LUNAR CRATERS, QUADRANT II by D. W. G. ARTHUR, ALICE P. AGNIERAY, RUTH A. HORVATH ,tl l C.A. WOOD AND C. R. CHAPMAN \_9 (_ /_) March 14, 1964 ABSTRACT The designation, diameter, position, central-peak information, and state of completeness arc listed for each discernible crater in the second lunar quadrant with a diameter exceeding 3.5 km. The catalog contains more than 2,000 items and is illustrated by a map in 11 sections. his Communication is the second part of The However, since we also have suppressed many Greek System of Lunar Craters, which is a catalog in letters used by these authorities, there was need for four parts of all craters recognizable with reasonable some care in the incorporation of new letters to certainty on photographs and having diameters avoid confusion. Accordingly, the Greek letters greater than 3.5 kilometers. Thus it is a continua- added by us are always different from those that tion of Comm. LPL No. 30 of September 1963. The have been suppressed. Observers who wish may use format is the same except for some minor changes the omitted symbols of Blagg and Miiller without to improve clarity and legibility. The information in fear of ambiguity. the text of Comm. LPL No. 30 therefore applies to The photographic coverage of the second quad- this Communication also. rant is by no means uniform in quality, and certain Some of the minor changes mentioned above phases are not well represented. Thus for small cra- have been introduced because of the particular ters in certain longitudes there are no good determi- nature of the second lunar quadrant, most of which nations of the diameters, and our values are little is covered by the dark areas Mare Imbrium and better than rough estimates. When the diameter lacks Oceanus Procellarum. The density of craters over precision, it appears in parentheses in the catalog. these extensive maria is too low to provide an ade- One additional map convention should be noted. quate network of landmarks. Accordingly, we have When a name on the map is enclosed in brackets, it placed increased emphasis on isolated elevations, may be assumed that there are no associated lettered many of which have been anonymous until now. In objects. This convention eliminates the ambiguities our map a large number of these have been indicated which must occur when one named object lies en- by lowercase Greek letters, following the conventions tirely within another. of Blagg and Mtiller's Named Lunar Formations. To avoid congestion in some limb regions, a few 2 D.W.G. ARTHUR, ALICE P. AGNIERAY, RUTH A. HORVATH, C. A. WOOD AND C. R. CHAPMAN anonymous craters have been omitted from the map. Our Langley is Schmidt's Regnault while our Aston The following are the new names introduced in is Blagg and Miiller's Ulugh Beigh E and M_idler's the second lunar quadrant: Ulugh Beigh. It should be noted that the designation Hermite French mathematician Otto Struve is now shortened to Struve since there is no other crater with that name. Sylvester British mathematician Poncelet French mathematician The maps of Comm. LPL No. 30 have now been Brianchon French mathematician published in one sheet (Lunar Designations and Positions, Quadrant I, D. W. G. Arthur and A. P. Desargues French mathematician Eddington British astronomer Agnieray. University of Arizona Press, April 1964), Cremona Italian mathematician and users of the latter publication should note that Boole British mathematician six names in the libratory zone are not mentioned in Comm. LPL No. 30. These are : Volta Italian physicist Markov Russian mathematician Goddard American physicist Moseley 1 British physicist Jansky American radio engineer Stokes British physicist Liapunov Russian mathematician Langley American astronomer Rayleigh British physicist Bunsen German chemist Riemann German mathematician R6ntgen: German physicist Boss American astronomer Aston British physicist The above formations were not designated in Named Russell American astronomer Lunar Formations. Balboa Spanish explorer The maps accompanying this Communication Dalton British chemist and physicist are extremely crowded in the limb region, and it Einstein American (German-born) physicist is clear that the standard orthographic projection is Bohr Danish physicist not suitable for the observation and identification Planck: German physicist of objects near the limb. The same is true of con- Fermi 1 American (Italian-born) physicist formal maps or maps based on rectified photographs, Hedin Swedish explorer since these do not bear much resemblance to the Some of these were designated by letters in foreshortened view presented to the observer. There- Named Lunar Formations, as follows" fore, we have commenced a series of special limb maps that show each limb region under favorable Sylvester = Philolaus P conditions of libration. These will supplement the Poncelet ---_ Anaximenes F maps in orthographic projection that accompany the Brianchon z Carpenter C various parts of The System of Lunar Craters. Pascal = Carpenter D The work was supported by the National Aero- Desargues = Anaximander C nautics and Space Administration under Grant No. Markov z Oenopides A NsG 161-61. Russell = N. component of Otto Struve Eddington = Otto Struve A :These craters lie beyond the mean limb and are not included in our catalog or shown in the maps. See Rectified Lunar Atlas by E. A. Whitaker et al., University of Arizona Press, I963. THE CATALOG Ref. B & M Designation × P D K C B C.E. 20008 858 Murchison -.002 +.089 +.996 -0.i +5.1 33.31 57.90 4f aMC 0 20014 .019 .047 .999 i .I 2.7 5.79 10.06 3 aMC p 20014A .019 .044 .999 i.I 2.5 2.91 5.06 2 pMC 0 20017 1229B Pallas C .019 .078 .997 i.i 4.5 4.07 7.07 2 C 0 20022 Pallas V .027 .029 .999 1.5 1.7 1.68 2.92 i pM 0 20025 .020 .053 .998 I.i 3.0 2.70 4.69 2 C 0 20026 Pallas F .023 .060 .998 1.3 3.4 11.03 19.17 4f aMC 0 20026A Pallas W .021 .062 .998 1.2 3.6 2.15 3.74 I pMC 0 20027 Pallas E .025 .070 .997 i .4 4.0 15.82 27.50 4f aMC 0 20028 Pallas H .027 .081 .996 i .6 4.6 3.07 5.34 i C 0 20029 1225 Pallas .028 .096 .995 1.6 5.5 28.52 49.57 3 C P 20036 .035 .063 .997 2.0 3.6 15.31 26.61 5f aMC 0 20037 .036 .074 .997 2.1 4.2 6.99 12.15 4 C 0 20044 1229A Pallas D .045 .041 .998 2.6 2.3 2.35 4.08 I pMC 0 20047 1227 Pallas B .045 .073 .996 2.6 4.2 2.20 3.82 I C 0 20047A .046 .074 .996 2.6 4.2 13.12 22.80 4 C 0 20059 Pallas X .056 .090 .994 3.2 5.2 1.64 2.85 i C 0 20069 1218A Bode L .066 .098 .993 3.8 5.6 2.66 4.62 I C 0 20070 1248A S_rmnering M .078 .000 .997 4.5 0.0 15.91 27.65 5f aMC 0 20087 .086 .076 .993 4.9 4.4 22.90 39.80 5f aMC 0 20092 .097 .029 .995 5.6 i .7 2.18 3.79 2 pMC 0 20115 1214 Bode A .020 .156 .988 1.2 9.0 7.10 12.34 i C 0 20119 Ukert J .010 .191 .982 0.6 ii .0 1.88 3.27 i C 0 20136 1217A Bode K .039 .162 .986 2.3 9.3 3.48 6.05 i C 0 20140 1226 Pallas A .040 .104 .994 2.3 6.0 6.09 10.59 i C 0 20141 1212 Bode .042 .117 .992 2.4 6.7 10.69 18.58 i C R 20151 .059 .118 .991 3.4 6.8 2.19 3.81 2 C 0 20152 1216 Bode D .057 .126 .990 3.3 7.2 2.15 3.74 2 C 0 20155 1215 Bode B .053 .152 .987 3.1 8.7 5.87 10.20 I C 0 20161 1213 Bode G .061 .II0 .992 3.5 6.3 2.53 4.40 I C 0 20166 (1251) Bode BA .069 .169 .983 4.0 9.7 2.61 4.54 i C 0 20169 Bode N .066 .190 .980 3.9 ii .0 3.49 6.07 3 C 0 20179 .075 .199 .977 4.4 ii .5 8.54 14.84 4 f aMC 0 20183 .082 .132 .988 4.7 7.6 2.09 3.63 3 C 0 1.44 2.50 20194 .097 .143 .985 5.6 8.2 2.04 3.55 2 C 0 20195 .094 .157 .983 5.5 9.0 9.96 17.31 4f aMC 0 20201 .007 .211 .977 0.4 12.2 11.67 20.28 4f aMC 0 20209 Marco Polo P .003 .291 .957 0.2 16.9 18.04 31.36 4f C 0 20213 Marco Polo T .017 .235 .972 1.0 13.6 i .80 3.13 i C 0 20235 1202 Marco Polo A .033 .257 .966 2.0 14.9 3.99 6.94 i C 0 20236 1201 Marco Polo .034 .266 .963 2.0 15.4 15.94 27.71 4 C 0 12.33 21.43 20236A .036 .263 .964 2 .i 15.2 2.10 3.65 I C 0 20238 1203A Marco Polo G .032 .287 .957 1.9 16.7 2.98 5.18 2 C 0 2 Ref.
Load more

Recommended publications
  • Texas Co-Op Power • March 2017
    LOCAL ELECTRIC COOPERATIVE EDITION MARCH 2017 Blizzard of ’57 Spring Vegetable Salads Palo Duro Pageant 35 35on Brake-worthy stops on highway through co-op country THE TRACTOR THAT STARTED IT ALL. IS CHANGING IT ALL. Metal Hood, Fenders New Deluxe Seat** New Swift-TTaach Loader** New Grille Guard New Dash Panel & Operator Platform & Tilt Steering Wheel & Swift-Connect Backhoe & Front Hitch & Display ALL-NEWW KUBOTTAA BX80 SERIES Low-Rate, Long-TTeerm Financing 6 YYeear Goingg On Noww! Limited Powertrain Warrantyy* kubota.com *Only terms and conditions of Kubota’s standard Limited Warranty applyy.. For warranty terms, see Kubota’s Limited Warranty at www.kubota.com or authorized Kubota Dealers. **Only avvaailable on certain models. Optional equipment may be shown. © Kubota TTrractor Corporation, 2017 Since 1944 March 2017 FAVORITES 5 Letters 6 Currents 18 Local Co-op News Get the latest information plus energy and safety tips from your cooperative. 29 Texas History Panhandle Blizzard of 1957 By Dawn Stephens 31 Recipes Spring Vegetable Salads 35 Focus on Texas Photo Contest: In Motion 36 Around Texas List of Local Events 38 Hit the Road Texas on a Grand Stage in Palo Duro By Sheryl Smith-Rodgers Marker near the northern end ONLINE of Interstate 35 in Texas, just TexasCoopPower.com south of the Red River Find these stories online if they don’t appear in your edition of the magazine. FEATURE Texas USA Odessa Meteor Crater 35 on 35 8 Stops with fascinating food, history and popular By E.R. Bills culture lure travelers from the interstate as it weaves Observations through Texas from Mexico to Oklahoma Another Roadside Attraction Story and photos by Julia Robinson By Ryann Ford ROAD TRIP! See video and photos at TexasCoopPower.com NEXT MONTH Drones: An Overview Texas inno- vators, including electric co-ops, hone drones as tools of today.
    [Show full text]
  • Copyrighted Material
    Index Abulfeda crater chain (Moon), 97 Aphrodite Terra (Venus), 142, 143, 144, 145, 146 Acheron Fossae (Mars), 165 Apohele asteroids, 353–354 Achilles asteroids, 351 Apollinaris Patera (Mars), 168 achondrite meteorites, 360 Apollo asteroids, 346, 353, 354, 361, 371 Acidalia Planitia (Mars), 164 Apollo program, 86, 96, 97, 101, 102, 108–109, 110, 361 Adams, John Couch, 298 Apollo 8, 96 Adonis, 371 Apollo 11, 94, 110 Adrastea, 238, 241 Apollo 12, 96, 110 Aegaeon, 263 Apollo 14, 93, 110 Africa, 63, 73, 143 Apollo 15, 100, 103, 104, 110 Akatsuki spacecraft (see Venus Climate Orbiter) Apollo 16, 59, 96, 102, 103, 110 Akna Montes (Venus), 142 Apollo 17, 95, 99, 100, 102, 103, 110 Alabama, 62 Apollodorus crater (Mercury), 127 Alba Patera (Mars), 167 Apollo Lunar Surface Experiments Package (ALSEP), 110 Aldrin, Edwin (Buzz), 94 Apophis, 354, 355 Alexandria, 69 Appalachian mountains (Earth), 74, 270 Alfvén, Hannes, 35 Aqua, 56 Alfvén waves, 35–36, 43, 49 Arabia Terra (Mars), 177, 191, 200 Algeria, 358 arachnoids (see Venus) ALH 84001, 201, 204–205 Archimedes crater (Moon), 93, 106 Allan Hills, 109, 201 Arctic, 62, 67, 84, 186, 229 Allende meteorite, 359, 360 Arden Corona (Miranda), 291 Allen Telescope Array, 409 Arecibo Observatory, 114, 144, 341, 379, 380, 408, 409 Alpha Regio (Venus), 144, 148, 149 Ares Vallis (Mars), 179, 180, 199 Alphonsus crater (Moon), 99, 102 Argentina, 408 Alps (Moon), 93 Argyre Basin (Mars), 161, 162, 163, 166, 186 Amalthea, 236–237, 238, 239, 241 Ariadaeus Rille (Moon), 100, 102 Amazonis Planitia (Mars), 161 COPYRIGHTED
    [Show full text]
  • Geoscience and a Lunar Base
    " t N_iSA Conference Pubhcatmn 3070 " i J Geoscience and a Lunar Base A Comprehensive Plan for Lunar Explora, tion unclas HI/VI 02907_4 at ,unar | !' / | .... ._-.;} / [ | -- --_,,,_-_ |,, |, • • |,_nrrr|l , .l -- - -- - ....... = F _: .......... s_ dd]T_- ! JL --_ - - _ '- "_r: °-__.......... / _r NASA Conference Publication 3070 Geoscience and a Lunar Base A Comprehensive Plan for Lunar Exploration Edited by G. Jeffrey Taylor Institute of Meteoritics University of New Mexico Albuquerque, New Mexico Paul D. Spudis U.S. Geological Survey Branch of Astrogeology Flagstaff, Arizona Proceedings of a workshop sponsored by the National Aeronautics and Space Administration, Washington, D.C., and held at the Lunar and Planetary Institute Houston, Texas August 25-26, 1988 IW_A National Aeronautics and Space Administration Office of Management Scientific and Technical Information Division 1990 PREFACE This report was produced at the request of Dr. Michael B. Duke, Director of the Solar System Exploration Division of the NASA Johnson Space Center. At a meeting of the Lunar and Planetary Sample Team (LAPST), Dr. Duke (at the time also Science Director of the Office of Exploration, NASA Headquarters) suggested that future lunar geoscience activities had not been planned systematically and that geoscience goals for the lunar base program were not articulated well. LAPST is a panel that advises NASA on lunar sample allocations and also serves as an advocate for lunar science within the planetary science community. LAPST took it upon itself to organize some formal geoscience planning for a lunar base by creating a document that outlines the types of missions and activities that are needed to understand the Moon and its geologic history.
    [Show full text]
  • Glossary Glossary
    Glossary Glossary Albedo A measure of an object’s reflectivity. A pure white reflecting surface has an albedo of 1.0 (100%). A pitch-black, nonreflecting surface has an albedo of 0.0. The Moon is a fairly dark object with a combined albedo of 0.07 (reflecting 7% of the sunlight that falls upon it). The albedo range of the lunar maria is between 0.05 and 0.08. The brighter highlands have an albedo range from 0.09 to 0.15. Anorthosite Rocks rich in the mineral feldspar, making up much of the Moon’s bright highland regions. Aperture The diameter of a telescope’s objective lens or primary mirror. Apogee The point in the Moon’s orbit where it is furthest from the Earth. At apogee, the Moon can reach a maximum distance of 406,700 km from the Earth. Apollo The manned lunar program of the United States. Between July 1969 and December 1972, six Apollo missions landed on the Moon, allowing a total of 12 astronauts to explore its surface. Asteroid A minor planet. A large solid body of rock in orbit around the Sun. Banded crater A crater that displays dusky linear tracts on its inner walls and/or floor. 250 Basalt A dark, fine-grained volcanic rock, low in silicon, with a low viscosity. Basaltic material fills many of the Moon’s major basins, especially on the near side. Glossary Basin A very large circular impact structure (usually comprising multiple concentric rings) that usually displays some degree of flooding with lava. The largest and most conspicuous lava- flooded basins on the Moon are found on the near side, and most are filled to their outer edges with mare basalts.
    [Show full text]
  • Planetary Surfaces
    Chapter 4 PLANETARY SURFACES 4.1 The Absence of Bedrock A striking and obvious observation is that at full Moon, the lunar surface is bright from limb to limb, with only limited darkening toward the edges. Since this effect is not consistent with the intensity of light reflected from a smooth sphere, pre-Apollo observers concluded that the upper surface was porous on a centimeter scale and had the properties of dust. The thickness of the dust layer was a critical question for landing on the surface. The general view was that a layer a few meters thick of rubble and dust from the meteorite bombardment covered the surface. Alternative views called for kilometer thicknesses of fine dust, filling the maria. The unmanned missions, notably Surveyor, resolved questions about the nature and bearing strength of the surface. However, a somewhat surprising feature of the lunar surface was the completeness of the mantle or blanket of debris. Bedrock exposures are extremely rare, the occurrence in the wall of Hadley Rille (Fig. 6.6) being the only one which was observed closely during the Apollo missions. Fragments of rock excavated during meteorite impact are, of course, common, and provided both samples and evidence of co,mpetent rock layers at shallow levels in the mare basins. Freshly exposed surface material (e.g., bright rays from craters such as Tycho) darken with time due mainly to the production of glass during micro- meteorite impacts. Since some magnetic anomalies correlate with unusually bright regions, the solar wind bombardment (which is strongly deflected by the magnetic anomalies) may also be responsible for darkening the surface [I].
    [Show full text]
  • Feature of the Month – January 2016 Galilaei
    A PUBLICATION OF THE LUNAR SECTION OF THE A.L.P.O. EDITED BY: Wayne Bailey [email protected] 17 Autumn Lane, Sewell, NJ 08080 RECENT BACK ISSUES: http://moon.scopesandscapes.com/tlo_back.html FEATURE OF THE MONTH – JANUARY 2016 GALILAEI Sketch and text by Robert H. Hays, Jr. - Worth, Illinois, USA October 26, 2015 03:32-03:58 UT, 15 cm refl, 170x, seeing 8-9/10 I sketched this crater and vicinity on the evening of Oct. 25/26, 2015 after the moon hid ZC 109. This was about 32 hours before full. Galilaei is a modest but very crisp crater in far western Oceanus Procellarum. It appears very symmetrical, but there is a faint strip of shadow protruding from its southern end. Galilaei A is the very similar but smaller crater north of Galilaei. The bright spot to the south is labeled Galilaei D on the Lunar Quadrant map. A tiny bit of shadow was glimpsed in this spot indicating a craterlet. Two more moderately bright spots are east of Galilaei. The western one of this pair showed a bit of shadow, much like Galilaei D, but the other one did not. Galilaei B is the shadow-filled crater to the west. This shadowing gave this crater a ring shape. This ring was thicker on its west side. Galilaei H is the small pit just west of B. A wide, low ridge extends to the southwest from Galilaei B, and a crisper peak is south of H. Galilaei B must be more recent than its attendant ridge since the crater's exterior shadow falls upon the ridge.
    [Show full text]
  • Special Catalogue Milestones of Lunar Mapping and Photography Four Centuries of Selenography on the Occasion of the 50Th Anniversary of Apollo 11 Moon Landing
    Special Catalogue Milestones of Lunar Mapping and Photography Four Centuries of Selenography On the occasion of the 50th anniversary of Apollo 11 moon landing Please note: A specific item in this catalogue may be sold or is on hold if the provided link to our online inventory (by clicking on the blue-highlighted author name) doesn't work! Milestones of Science Books phone +49 (0) 177 – 2 41 0006 www.milestone-books.de [email protected] Member of ILAB and VDA Catalogue 07-2019 Copyright © 2019 Milestones of Science Books. All rights reserved Page 2 of 71 Authors in Chronological Order Author Year No. Author Year No. BIRT, William 1869 7 SCHEINER, Christoph 1614 72 PROCTOR, Richard 1873 66 WILKINS, John 1640 87 NASMYTH, James 1874 58, 59, 60, 61 SCHYRLEUS DE RHEITA, Anton 1645 77 NEISON, Edmund 1876 62, 63 HEVELIUS, Johannes 1647 29 LOHRMANN, Wilhelm 1878 42, 43, 44 RICCIOLI, Giambattista 1651 67 SCHMIDT, Johann 1878 75 GALILEI, Galileo 1653 22 WEINEK, Ladislaus 1885 84 KIRCHER, Athanasius 1660 31 PRINZ, Wilhelm 1894 65 CHERUBIN D'ORLEANS, Capuchin 1671 8 ELGER, Thomas Gwyn 1895 15 EIMMART, Georg Christoph 1696 14 FAUTH, Philipp 1895 17 KEILL, John 1718 30 KRIEGER, Johann 1898 33 BIANCHINI, Francesco 1728 6 LOEWY, Maurice 1899 39, 40 DOPPELMAYR, Johann Gabriel 1730 11 FRANZ, Julius Heinrich 1901 21 MAUPERTUIS, Pierre Louis 1741 50 PICKERING, William 1904 64 WOLFF, Christian von 1747 88 FAUTH, Philipp 1907 18 CLAIRAUT, Alexis-Claude 1765 9 GOODACRE, Walter 1910 23 MAYER, Johann Tobias 1770 51 KRIEGER, Johann 1912 34 SAVOY, Gaspare 1770 71 LE MORVAN, Charles 1914 37 EULER, Leonhard 1772 16 WEGENER, Alfred 1921 83 MAYER, Johann Tobias 1775 52 GOODACRE, Walter 1931 24 SCHRÖTER, Johann Hieronymus 1791 76 FAUTH, Philipp 1932 19 GRUITHUISEN, Franz von Paula 1825 25 WILKINS, Hugh Percy 1937 86 LOHRMANN, Wilhelm Gotthelf 1824 41 USSR ACADEMY 1959 1 BEER, Wilhelm 1834 4 ARTHUR, David 1960 3 BEER, Wilhelm 1837 5 HACKMAN, Robert 1960 27 MÄDLER, Johann Heinrich 1837 49 KUIPER Gerard P.
    [Show full text]
  • Pfizer Vaccine
    Find a Walgreens near you to receive an additional dose of the Pfizer COVID-19 vaccine Vaccines subject to availability, State-, age-, and health-related restrictions may apply. PFIZER STORES State Store Address City Zipcode AK 15092 1470 W NORTHERN LIGHTS BLVD ANCHORAGE 99503 AK 13656 725 E NORTHERN LIGHTS BLVD ANCHORAGE 99503 AK 12680 2197 W DIMOND BLVD ANCHORAGE 99515 AK 15653 4353 LAKE OTIS PARKWAY ANCHORAGE 99508 AK 13449 12405 BRANDON ST ANCHORAGE 99515 AK 15654 2550 E 88TH AVE ANCHORAGE 99507 AK 15362 12051 OLD GLENN HWY EAGLE RIVER 99577 AK 15944 530 OLD STEESE HWY FAIRBANKS 99701 AL 9951 9301 HIGHWAY 119 ALABASTER 35007 AL 11279 7155 US HIGHWAY 431 ALBERTVILLE 35950 AL 11819 1401 GOLDEN SPRINGS RD ANNISTON 36207 AL 19256 2413 HIGHWAY 431 NORTH ANNISTON 36206 AL 7951 800 QUINTARD AVE ANNISTON 36201 AL 11651 4700 HIGHWAY 280 BIRMINGHAM 35242 AL 6034 101 GREEN SPRINGS HWY BIRMINGHAM 35209 AL 7791 101 DOUG BAKER BLVD BIRMINGHAM 35242 AL 7245 668 LOMB AVE SW BIRMINGHAM 35211 AL 7306 4496 VALLEYDALE RD BIRMINGHAM 35242 AL 6035 2101 RICHARD ARRINGTON JR BLVD S BIRMINGHAM 35209 AL 15144 3020 CLAIRMONT AVE S BIRMINGHAM 35205 AL 10333 3150 GREEN VALLEY RD BIRMINGHAM 35243 AL 11469 9325 PARKWAY E BIRMINGHAM 35215 AL 4846 2301 CENTER POINT PKWY BIRMINGHAM 35215 AL 10965 920 US HIGHWAY 431 BOAZ 35957 AL 11531 16468 HIGHWAY 280 CHELSEA 35043 AL 15205 444 2ND AVE NW CULLMAN 35055 AL 11180 1700 2ND AVE SW CULLMAN 35055 AL 5606 3025 US HIGHWAY 98 DAPHNE 36526 AL 9976 1127 6TH AVE SE DECATUR 35601 AL 7404 2041 E MAIN ST DOTHAN 36301 AL 7405 2940
    [Show full text]
  • Planetary Science : a Lunar Perspective
    APPENDICES APPENDIX I Reference Abbreviations AJS: American Journal of Science Ancient Sun: The Ancient Sun: Fossil Record in the Earth, Moon and Meteorites (Eds. R. 0.Pepin, et al.), Pergamon Press (1980) Geochim. Cosmochim. Acta Suppl. 13 Ap. J.: Astrophysical Journal Apollo 15: The Apollo 1.5 Lunar Samples, Lunar Science Insti- tute, Houston, Texas (1972) Apollo 16 Workshop: Workshop on Apollo 16, LPI Technical Report 81- 01, Lunar and Planetary Institute, Houston (1981) Basaltic Volcanism: Basaltic Volcanism on the Terrestrial Planets, Per- gamon Press (1981) Bull. GSA: Bulletin of the Geological Society of America EOS: EOS, Transactions of the American Geophysical Union EPSL: Earth and Planetary Science Letters GCA: Geochimica et Cosmochimica Acta GRL: Geophysical Research Letters Impact Cratering: Impact and Explosion Cratering (Eds. D. J. Roddy, et al.), 1301 pp., Pergamon Press (1977) JGR: Journal of Geophysical Research LS 111: Lunar Science III (Lunar Science Institute) see extended abstract of Lunar Science Conferences Appendix I1 LS IV: Lunar Science IV (Lunar Science Institute) LS V: Lunar Science V (Lunar Science Institute) LS VI: Lunar Science VI (Lunar Science Institute) LS VII: Lunar Science VII (Lunar Science Institute) LS VIII: Lunar Science VIII (Lunar Science Institute LPS IX: Lunar and Planetary Science IX (Lunar and Plane- tary Institute LPS X: Lunar and Planetary Science X (Lunar and Plane- tary Institute) LPS XI: Lunar and Planetary Science XI (Lunar and Plane- tary Institute) LPS XII: Lunar and Planetary Science XII (Lunar and Planetary Institute) 444 Appendix I Lunar Highlands Crust: Proceedings of the Conference in the Lunar High- lands Crust, 505 pp., Pergamon Press (1980) Geo- chim.
    [Show full text]
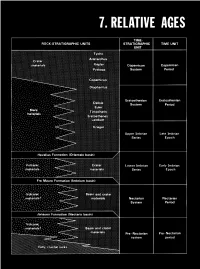
  • Relative Ages
    CONTENTS Page Introduction ...................................................... 123 Stratigraphic nomenclature ........................................ 123 Superpositions ................................................... 125 Mare-crater relations .......................................... 125 Crater-crater relations .......................................... 127 Basin-crater relations .......................................... 127 Mapping conventions .......................................... 127 Crater dating .................................................... 129 General principles ............................................. 129 Size-frequency relations ........................................ 129 Morphology of large craters .................................... 129 Morphology of small craters, by Newell J. Fask .................. 131 D, method .................................................... 133 Summary ........................................................ 133 table 7.1). The first three of these sequences, which are older than INTRODUCTION the visible mare materials, are also dominated internally by the The goals of both terrestrial and lunar stratigraphy are to inte- deposits of basins. The fourth (youngest) sequence consists of mare grate geologic units into a stratigraphic column applicable over the and crater materials. This chapter explains the general methods of whole planet and to calibrate this column with absolute ages. The stratigraphic analysis that are employed in the next six chapters first step in reconstructing
    [Show full text]
  • Weiler2006.Pdf (5.444Mb)
    Study of the Gas and Dust Activity of Recent Comets vorgelegt von Diplom-Physiker Michael Weiler aus Andernach Von der Fakult¨at II - Mathematik und Naturwissenschaften der Technischen Universit¨at Berlin zur Erlangung des akademischen Grades Doktor der Naturwissenschaften Dr. rer. nat. genehmigte Dissertation Promotionsausschuss: Vorsitzender: Prof. Dr.-Ing. Hans Joachim Eichler Berichter/Gutachter: Prof. Dr. rer. nat. Heike Rauer Berichter/Gutachter: Prof. Dr. rer. nat. Erwin Sedlmayr Tag der wissenschaftlichen Aussprache: 18.12.2006 Berlin 2007 D 83 1 Contents 0 Zusammenfassung 6 1 Introduction 7 1.1 Historical Development of Comet Science in Brief . ...... 7 1.2 Short Overview of the Present Picture of Comets . ..... 7 1.2.1 TheCometaryNucleus ........................ 8 1.2.2 TheDustComaandTail........................ 9 1.2.3 TheNeutralComa ........................... 10 1.2.4 ThePlasmaEnvironment . 10 1.2.5 Dynamical Classification of Comets . 11 1.2.6 CometarySourceRegions . 12 1.2.7 Classification according to the Coma Composition . 13 1.2.8 Correlations between Taxonomy, Source Regions, and Formation RegionsofComets ........................... 14 1.3 The Formation Chemistry of C2 and C3 ................... 15 1.4 Goalsofthiswork................................ 16 2 Optical Comet Observations 19 2.1 OpticalEmissionsfromComets . 19 2.1.1 GasEmissions.............................. 19 2.1.2 Light Scattering by Dust Particles . 20 2.1.3 OpticalObservationsoftheNucleus. 21 2.2 Overview of Observational Techniques . 22 2.2.1 Long-SlitSpectroscopy . 22 2.2.2 Imaging ................................. 23 2.3 ObservationalDatasetofthisWork . 23 2.3.1 Observations of Comet 67P/Churyumov-Gerasimenko . 24 2.3.2 Observations of Comet 9P/Tempel 1 . 27 2.3.3 Observations of Comets C/2002 T7 LINEAR and C/2001 Q4 NEAT 28 2.3.4 Reference Observations of Comet C/1995 O1 Hale-Bopp .
    [Show full text]
  • Meet the Philosophers of Ancient Greece
    Meet the Philosophers of Ancient Greece Everything You Always Wanted to Know About Ancient Greek Philosophy but didn’t Know Who to Ask Edited by Patricia F. O’Grady MEET THE PHILOSOPHERS OF ANCIENT GREECE Dedicated to the memory of Panagiotis, a humble man, who found pleasure when reading about the philosophers of Ancient Greece Meet the Philosophers of Ancient Greece Everything you always wanted to know about Ancient Greek philosophy but didn’t know who to ask Edited by PATRICIA F. O’GRADY Flinders University of South Australia © Patricia F. O’Grady 2005 All rights reserved. No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording or otherwise without the prior permission of the publisher. Patricia F. O’Grady has asserted her right under the Copyright, Designs and Patents Act, 1988, to be identi.ed as the editor of this work. Published by Ashgate Publishing Limited Ashgate Publishing Company Wey Court East Suite 420 Union Road 101 Cherry Street Farnham Burlington Surrey, GU9 7PT VT 05401-4405 England USA Ashgate website: http://www.ashgate.com British Library Cataloguing in Publication Data Meet the philosophers of ancient Greece: everything you always wanted to know about ancient Greek philosophy but didn’t know who to ask 1. Philosophy, Ancient 2. Philosophers – Greece 3. Greece – Intellectual life – To 146 B.C. I. O’Grady, Patricia F. 180 Library of Congress Cataloging-in-Publication Data Meet the philosophers of ancient Greece: everything you always wanted to know about ancient Greek philosophy but didn’t know who to ask / Patricia F.
    [Show full text]