2.5. Chiral Perturbation Theory
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Acta Centri Lucusiensis
ACTA CENTRI LUCUSIENSIS nr. 2B/2014 Centrul de studii DacoRomanistice LUCUS Timişoara ISSN 2343-8266 ISSN-L 2343-8266 http://www.laurlucus.ro Colegiul ştiinţific coordonator: prof. univ. dr. Dan Negrescu secretar: prof. univ. dr. Sergiu Drincu membri: prof. univ. dr. Ştefan Buzărnescu lect. univ. dr. Valy-Geta Ceia lect. univ. dr. Călin Timoc membru de onoare: cerc. şt. dr. Leonard Velcescu (Perpignan, Franţa) Colegiul de redacţie director: Laurenţiu Nistorescu secretar de redacţie: Daniel Haiduc redactori: Cătălin Borangic Antuza Genescu Daniela Damian Responsabilitatea asupra conţinutului articolelor aparţine în mod exclusiv autorilor 3 Cuprins Argument Laurenţiu Nistorescu _6 Ficţiunea retragerii aureliene şi destructurarea sa conceptuală Studii şi însemnări V.D. Călărăşanu 18 Însemnări privind relaţia regalităţii geto-dacice cu sacerdoţiul dionisiac Bogdan Muscalu 23 Tradiţii romane în istoria serviciilor de intelligence Constantin Elen 37 Din nou despre termenul limigantes Dan Negrescu 39 Despre o menţiune ieronimiană Remus Mihai Feraru 42 Relațiile dintre Biserică și stat în viziunea Sfântului Maxim Mărturisitorul Convergenţe Sergiu Enache 57 Două topoare de luptă din fier descoperite la Gătaia Sorin Damian 62 Repere evenimenţiale în evoluţiile de la Dunăre din secolele VIII-IX Lecturi critice Claudia S. Popescu 67 Chestiunea celţilor intracarpatici şi câteva prezumţii de relativizat 4 Daniela Damian 71 Semnal: Peuce XII/2014 Basarab Constantin 73 Kallatida, prefigurarea unei monografii Dosar DakkHabbit Daniel Haiduc 76 DakHabbit: Investigaţii cartodinamice ale habitatului Daciei preromane Cătălin Borangic, Alexandru Berzovan 82 Concepte despre cetatea dacică (I) 5 Argument 6 Laurenţiu Nistorescu Ficţiunea retragerii aureliene şi destructurarea sa conceptuală1 The fictionality of the Aurelian withdrawal and its conceptual dismantle Abstract: The “Aurelian withdrawal” phrase appeared as a result of misreading the literary sources and a simplistic – and sometimes tendentious – perception of the historical processes. -

Avisos Del Diario Oficial
DiarioOficial | Nº 30.734 - julio 28 de 2021 Avisos 11 JULIO MARÍA POSE POMBO (IUE 2-23617/2021). Montevideo, 12 de julio de 2021. MARIA VICTORIA GIOVANELLI FERREIRA, Actuario Adjunto. 01) $ 6913 10/p 12618 Jul 20- Ago 02 ALFREDO BREITFELD (IUE 2-9980/2021). Montevideo, 05 de julio de 2021. MARIA VICTORIA GIOVANELLI FERREIRA, SEGUNDO TURNO Actuario Adjunto. 01) $ 6913 10/p 12550 Jul 20- Ago 02 JESÚS PARDO AGRA y de SYLVIA ALEJANDRA PARDO PEREYRA (IUE LUIS CARLOS PEREIRA (IUE 2-23262/2021). 2-59898/2020). Montevideo, 12 de julio de 2021. Montevideo, 04 de junio de 2021. MARIA VICTORIA GIOVANELLI FERREIRA, MARIA VICTORIA GIOVANELLI FERREIRA, Actuario Adjunto. Actuario Adjunto. 01) $ 6913 10/p 12497 Jul 20- Ago 02 PODER JUDICIAL 01) $ 6913 10/p 13417 Jul 26- Ago 06 VALENTIN RODRÍGUEZ PÉREZ (IUE CARLOS ADOLFO MARIÑO MOLINARI 2-23417/2021). (Ley 16.044 Arts. 3o., 4o. y 5o.) (IUE 2-9047/2021). Montevideo, 12 de julio de 2021. Los señores Jueces Letrados de Familia han Montevideo, 12 de julio de 2021. MARIA VICTORIA GIOVANELLI FERREIRA, dispuesto la apertura de las Sucesiones MARIA VICTORIA GIOVANELLI FERREIRA, Actuario Adjunto. que se enuncian seguidamente y citan y Actuario Adjunto. 01) $ 6913 10/p 12447 Jul 20- Ago 02 emplazan a los herederos, acreedores y demás 01) $ 6913 10/p 13355 Jul 26- Ago 06 interesados en ellas, para que, dentro del MARIA IDISGLADEZ MORENO LAGO (IUE término de TREINTA DÍAS, comparezcan a ROBERTO DUERA FULINE (IUE 2-60251/2020). 2-58261/2020). deducir en forma sus derechos ante la Sede Montevideo, 12 de julio de 2021. -

Desintegraciones Hadrónicas Y Radiativas Del Leptón
Desintegraciones hadr´onicas y radiativas del lept´on tau: τ (P P P ) ντ , τ P γντ − → − − → − Pablo Roig Garc´es IFIC, Departament de F´ısica Te`orica Tesis doctoral Director: Jorge Portol´es Ib´a˜nez Val`encia, a 15 de Noviembre de 2010 JORGE PORTOLES´ IBA´NEZ,˜ Cient´ıfico Titular del Instituto de F´ısica Cor- puscular de Val`encia, CERTIFICA Que la presente memoria “Desintegraciones hadr´onicas y radiativas del lept´on tau” ha sido realizada bajo su direcci´on en el Departament de F´ı- sica Te`orica de la Universitat de Val`encia, por PABLO ROIG GARCES´ y constituye su Tesis para optar al grado de Doctor en F´ısica. Y para que as´ı conste, en cumplimiento de la legislaci´on vigente, presenta en el Departament de F´ısica Te`orica de la Universitat de Val`encia la referida Tesis Doctoral, y firma el presente certificado. Val`encia, a 4 d’Octubre de 2010. Jorge Portol´es Ib´a˜nez A mi madre, por todo y por siempre; y a Maru, por aguantarme durante la redacci´on de esta Tesis. ´Indice general 1. Introducci´on 1 1.1. Introducci´ongeneralalproblema . 1 1.2. La F´ısica del τ .............................. 3 1.3. QCD: la teor´ıade la interacci´on fuerte . 9 1.4. Las Teor´ıas Cu´anticas de Campos Efectivas . 12 1.5. Teor´ıaQuiraldePerturbaciones . 15 1.6. El l´ımite de gran n´umero de colores de QCD .............. 17 1.7. LaTeor´ıaQuiraldeResonancias. 18 1.8. Organizaci´ondelaTesis . 20 2. Introduction 21 2.1. -

¿CALVO? Órganos Genitales
EL DILUVIO DIARIO REPUBLICANO Aflo LXYII — Nóm. 91 a Barcelona — Miércoles, 16 de abril de 1924 • 10 céntimos Redtccfón. Adtnlnlstncidt T Talleres ESCUD1LLERS BUNCHS 8 bU Teléf A-e30 • Annndos y Sascripriones: PLAZA REAL, 7 SUSCUfCIOB etretiooi, «tu. I u au. nnn, KU rw tnaisirt.-fortngu. imtrtu » fnipinu, ftu. I'M irmiiln. Dnob paun, plu U (riaulrt. kJ/^DO A M JICJinLernas 0 externas, grietas, ele, recién inV^r\T\nPlncOl<-,s o crónicas. Absolutamente segura ia AVISO curación con POMADA AN£MA-SMITH. Ultimo adelanto de la cien• Conviene a toda señora, caballero j cia médica. iMillares de curaciones! Basta un solo tabú. No lo dude niño comprar sus guardapolvos, batai tfd. 5 pts. caja. Segalá, R. Flores 14: Alsina, P. Crédito. 4: Oru» Ra o trajea en los almacenes EL. LOUVRE la EscudiMers "15: Salus Fonfanella 7; S*rra Pelayo S y farmacias Carmen, 38. MAL.^ DECRETOS IMPOTENCIA. MATRIZ : Iralamientos modernos sin dolor. — Rambla, Llano Boquerla, número R entre calle Hospital i San Piblo. De 9a12vdp3a8. Festivos, de 9 a 12 SIFILIS Desarrollo, beileza y emlur-. cimiento en dos meses con PILDORAS Específicos SELLES CIRCASIANAS del PECHOS doctor BRUN El rey de la sangre humana |37 año» de éiitc mundial es el meict reclamol seis pesetas Irasco (l'ATKMADO) Scgalá. R. Rotes, 14; Alsina. P Crédito, 4; Vicente Ferrer y C.1 Garantizado por la Ley Infernac onal Cruz Roja, Escudillers, número 75; Salus, Fontanclla, 7; Sena, ile Puros Alimenlos de 30 de Junio de Pelayo, 9; Farmacia Moderna, Hospital, 2, v tarmacias ¿zar 1906. CURACION RADICAL DE LA SIFILIS EXTIRPACION RADICAL CN 40 DIAS con todas sus derivaciones (por la electrlelrta'V crónicas y hereditarias, locos, mudos, PELO Absolulamenle ga antizada. -

O Mineiro Moçambicano
UNIVERSIDADE EDUARDO MONDLANE CENTRO DE ESTUDOS AFRICANOS O MINEIRO MOÇAMBICANO Um estudo sobre a exportaçāo de māo de obra Introdução e Capítulo I: A exportaçāo de māo de obra. 1977 Published in 2012 by the Ruth First Papers Project www.ruthfirstpapers.org.uk UNIVERSIDADE EDUARDO MONbLAME CENTRO DE ESTUDOS AFRICANOS UM ESTUDO SOBRE A EXPORTACAO DE MAO DE OBRA* f c'- - I l>.,$i ; C M 7 rnapuro- Director do Pmjecto: Ruth First Membms e Associadw. do de Estudos Africanos AnMnio Pachem (directorcadjunh) Eulslia de Brito Lufs de Brito -Nogueira da Costa Miguel da Cruz Ana Maria Loforte Kurt UadtSrin --Marta Maddrin Alpheus Manghesi Barry Munslow David Wield Marc Wuyts Outms membros das Brigadas que alizaram Trabalho do Cempo: Ricardo Bambo Jose CapGo Ernesto Cossa Jacqueline de Vries Valente Jarnine Atarias Mandevo Armando Machava Eudlia Mascarenhas Samuel ~alomkMatrJ11Juane Arlindo Moises bra go Muhai ConceiGGo Quadms Emfdio Ricardo June Stephen ~alombZandamela ~rnvfncia de Inhambane - partici- pantes nas Brigadas: Carlos Mfirio Chambale Ven^ancio Cuarnbe Miguel c. :a" - Rafael Mussanhane Paulino -1'' ; +W,- S- ,,-L JCflio Thai Pascoiil Watch Helena Dolny Diana Jelley Sri Nimpuno Adorindo Santos Rosalie Clough Ests project0 40 poderio scr levado- a cab0 sern o apoio das seguintes eetrwturas e serviws: - Ministru do Trabalho - Govsrnador da Provfncia de Inhambm - Aeitor da Universidade Eduardo Mondlane - Director do. Instituto de ~nvestiga~zoCienldfica - Director do Cantro de Estudos Africanos - Governador do Banca de Mu~ambique V Minist4rio -
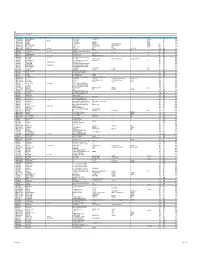
Details of Shareholders Unclaimed
HCC CONSECUTIVE OUTSTANDING PHY AND ELC RECORDS DIV PAY DATE 14-06-2011 SrNo Folio No/DPID ClientID 1st Holder Name 1st Joint Holder 2nd Joint Holder Add Line 1 Add Line 2 Add Line 3 Add Line 4 Add State Add Pincode Cumrrent Holding Amount_14JUN11 1 1201320000260366 SHIRODE ASHABAI VAMAN AT POST - SAYGAON TAL. CHALISGAON JALGAON 100 40.00 2 1203450000046694 MANISHA DANA Suvajit Dana B-1/135, KALYANI, NADIA 50 20.00 3 1201130000108840 ANITA MODI 410, A SILVER MALL, 8, RNT MARG, INDORE 40 16.00 4 1206850000006279 VIBHA RANGA W/O RAJESH RANGA KARMISAR ROAD OUT SIDE NATHUSAR GATE BIKANER 33401 40 16.00 5 1201060100100743 AMRISH NARESH SAXENA H. NO. 17 KABIR NIWAS MGIMS CAMPUS, SEWAGRAM WARDHA 42102 420 114.40 6 1201060100048428 Manoj Kumar Yadav Subhama Vihar Colony Lafagarh Gas , Godam Mangla Bilaspur 47751 100 40.00 7 IN30023910776917 RAHUL DUGGAL Shaveta Kapoor 15TH FLOOR SMSD PO BOX 3838 ABUDHABI, UAE 100000 600 240.00 8 IN30023911246780 OTTAKATH CHATHUNTAKAYIL KUTTIAMU P O BOX 61999 ABUDHABI U A E U A E 100000 600 240.00 9 HKA0009149 ASHOK KUMAR GULANI Padmaja Gulani 4/2 SINGLE STOREY RAMESH NAGAR NEW DELHI 110001 1000 400.00 10 HKB0040862 B S YADAV EDUCATION JCO HQ 502 AD GP (SP) C/O 56 APO DELHI 110001 500 400.00 11 HKC0264587 COLOMPRAKASH AWASTHY 11 CORPS PROVOST UNIT C/O 56 APO DELHI 110001 250 200.00 12 HKD0255276 DIPANKAR BANERJEE Sandhya Banerjee IDSA SAPRU HOUSE BARAKHAMBA ROAD NEW DELHI 110001 1500 1,200.00 13 HKK0006845 KARUNA SHARMA Raman Kumar H NO D-2 RANA PARTAP BAGH G T ROAD DELHI 110001 1000 800.00 14 HKN0259201 NEERJA -

(Nleopoldo'iii Comunica Al!Parlamento Su Decision
iiuiiidiupuin MAÑANA COMENZAN Diario Burgos LAS TAREAS DE LOS Año LX - Núm, 18.464 - Miércoles 2 de Agosto de 1950 - Apartado 46 - Teléfono 2015 - 50 céntimos CURSOS DE VERANO PARA EXTRANJEROS (NLEOPOLDO'III COMUNICA AL!PARLAMENTO Mas de 200*alumno5 se han mafriculado ya Hoy por la tarde llegarán a nuestra ciudad la mayor pane de los eslu- dlárttes extranjeros que vienen a los cur>os de verana que se celebraran en el SU DECISION DE DELEGAR LOS PODERES instituto Nacional de Enseñanza Media. , , , Pertenecen odos a distintas nacionalidades, predominando los franceses. F] viaje 1c han realizado en tren-hasta Bayona y desde Bayona a.Burgos en au- tecares ,que comenzarán a llegar a nuestra ciudad de cinco a seis de la REALES EN EL PRINCIPE BALDUINO tarde, marchando directamente al Instituto. Mañana, dia 3, a las diez de la mañana'; se reunirán todos les es.i:-, -wwv iiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiniiiiiiiiimiiiiiiiiiiiiiiiiiiimiiiii dianles en el Instituto para recibir las instrucciones generales de los Cursos, temonzando inmedialamenle tedas las enseñanzas. Al frente de la expedición viene Mr. Merimce, profesor de español de la Universidad de Toulcuse. _ las cuatro de la madrugada [lima i pilií tlll , l\ domingo, dia (>, y después de la misa del Espíritu Santo, que se ce• lebrará a las diez y media en la Iglesia del Carmen, se verificará la sesión • 'e apertura de ks Cjrsos en el Paraninfo del Instljulo, cqri asistencia de auto- r.'dados extranjeras, provinciales y lecah s. Monarca presidió una reuniónfl81 clp",0 "Cíi Ps'ará encargado de la cración inaugural el catedrático de I.P.era'ura de dicho Instituto, don Juan:,. -

La Revista De Taos, 10-18-1907 Jose ́ Montaner
University of New Mexico UNM Digital Repository Revista de Taos, 1905-1922 New Mexico Historical Newspapers 10-18-1907 La Revista de Taos, 10-18-1907 Jose ́ Montaner Follow this and additional works at: https://digitalrepository.unm.edu/revista_taos_news Recommended Citation Montaner, Jose.́ "La Revista de Taos, 10-18-1907." (1907). https://digitalrepository.unm.edu/revista_taos_news/88 This Newspaper is brought to you for free and open access by the New Mexico Historical Newspapers at UNM Digital Repository. It has been accepted for inclusion in Revista de Taos, 1905-1922 by an authorized administrator of UNM Digital Repository. For more information, please contact [email protected]. Lic. f'j? ... í TO ADVERTISERS. O - None of iiu'ri'-iwiii- in , te Northern Nc-v- r can If you want to progress in "ta- -x r !'X-- :í they do buiacs,-- -- have íuccv. and want the Mexican r i (ill i U i ' 1 patronage, you have to adver- MM ft i 'I í tiut advertido m tbia i spftr. f l I i l tise in this paper; bus the lar-pv- st v circulation in New México. J I We oifer our post office to verify Our cireidat ion guar.'iiiteist it L 2J00 copes every V, ii fffK. í Periódico Iliberal é Independiente. ER, I M- - JOSE MONTAN j M' de Montaner' Lditob v Pbopiwakio. TiemTolan Los Tiranos a la "Vos de la Pionca Independiente, Sf.cketakir Rarrim:. Año VI. Taos, Nuevo México, U. S. A., Viernes 18 de Octubre, 1907. No. 41 Lo que debe hacerse. -

După 378 Cu Privire Specială La Provincia Dacia Ripensis
Prăbuşirea apărării romane de frontieră la Dunărea de Mijloc şi de Jos după 378 cu privire specială la provincia Dacia Ripensis Nicolae GUDEA 1. Goţii la Dunărea de Jos de la mijlocul secolului III până la 378 Capitolul acesta se vrea o schiţă introductivă la evenimentele militare de la sfârşitul secolului IV, evenimente care au dus la prăbuşirea graniţei romane pe Dunăre. Nu avem deci intenţia de a realiza o istorie exhaustivă a goţilor în perioada menţionată. S-au scris despre ei numeroase lucrări mai generale (Wolframm 1990; Kazanski 1991; Bierbrauer 1994), zonale: Rusia, Ucraina (Magomedov 2001) sau locale: România (Ioniţă 1972; Harhoiu 1990). Cea mai completă lucrare referitoare la goţi, care îmbină sursele scrise cu realitatea arheologică este cea a lui B. Magomedov (Magomedov 2001). În această lucrare autorul prezintă evoluţia cronologică a mişcării goţilor dinspre nord spre sud, cultura lor materială şi a fixat relativ bine limitele lor spre teritoriul provinciilor dacice. El a stabilit trei perioade mari de răspândire şi dezvoltare a culturii lor materiale: 1. perioada 230-270 când gotii coboară spre sud atingând ţărmul de nord al Mării Negre, ajungând în sudul Moldovei şi în Câmpia Munteană. Este perioada marilor atacuri asupra Imperiului Roman din Moesia Inferior până în Pont şi Bithynia, urmate de reîntoarcerea în teritoriile de "baştină" (Magomedov 2001, 28 7, fig. 88); II. 270-330, perioadă de linişte relativă în care lipsesc aproape total atacurile asupra Imperiului (Magomedol' 2001, 288, fig. 89); III. 330-3 78, perioadă de atacuri generale asupra graniţei romane, urmată de stabilirea pe teritoriul Imperiului, mai ales în provinciile de la Dunărea de Mijloc şi de Jos (Magomedov 2001, 289, fig. -

MAL.BS SECRETOS R8ot,JERN,Ctar,Sl3at8^,L:,S; Tratamientos Modernos Sin Dolor.— Rambla, Llano Boqu^Rfa, Número 6, Entre Calle Hospital Y San Pablo
Afio LXV—Núm. 97 Barcelona.— Miérccles 3 de Mayo de 1922 i O céntimos DIARIO REPUBLICANO {ledaccwn, Administradón y Talleres: ESCUDILLERS BLANCHS, 3 bis.- Te^f. 630-a.—Annndos y Suscripciones: PLAZA REAL. 7 -n.CKsJL SUSORiPCIOW: Baroelona, ptaa. 2 ai mes. — Fucpa, ptai>. 7'50 trlnwslre. Portugal, Amér-Ioa y F'liplnas, ptas- S'BO trimestro. — Demás pcfses, ptas. IB trlmosti-a f ANTO DEL DIA: — -olpmnWad d9 fian José J lí Invfcnclía'rte la Santa Cruz ¡Sale el sol a la» !'.•£ mafíana.—Se pono a tas ({10 tarde.—Salo la Luna a las 10'4 luaílana.—se ponú a las 11°I6 marmr.a I E^^^tJBB BtM tí ^ inlprna- u externas, grietas, ele, recién .klvilvRavATCArO o irrrtnieas. Absolulamenlc segura la b«ii<u y a curación coa POMADA AWEMA-SIWITH. Ultimo adelanto de la cien• PECHOS duftclnucnt cia médica. ¡Millares de curaciones! Basta un solo tabo. tío lo dud# MiconiuPit'DO'a&s ciaoAsiA Vd. 5 pts. caja. Scgalá, R. Flores 14: Alsina, 1'. Crédito. 4; Crux Ro. B AS ít\ Dz P»i4. Broa. Inoltnu»», UcBipic bwrflciow • !• ulvd. Rtcomca ja Escúdillers 75; Salas Ko ntanella 7; Serra Pelayo 9 y farmae.as did<i poi rmUacUi mídicn iJS ifioi * «lio •sadltl! • P tááwé» aSTo mÉü& sor caos ¿roSteriM.0^ «irtnj. P Oldllo. i; V. »*• f C*. P'« C.:«lufli. 13; en 30 anos práctica Clínica, cura a toda edad, y por crónico sea d caso. Ja soi* K>><. *• KIoi«, «; Ollrtr. Ho^li»!. 3 y prto- <kra y zumbidos de oídos que privan oir.. Uso iácil, sin peli&ro y de acción rá^ t)alc» ftrniÉclti.— Mandando 6*50 pías ca te- tyf d* coir«o • Giro Peslat • Pou» Atehé, pida al órgano auditivo, que sensibiliza y vitifica. -

£/ Gobierno Encubre CQRRÜPCÍQK ADMINISTRATIVA
bemoauo n»i rAK-niHi FDiriON DK l> rAfUNAe COMI MSI A Dfc CtMOMMl A Bniota. acaato 11 N IMS B(r«r««r. Na. IM (Mí) » Vn jawtis MUIUSO DIAZ C'lIlCt'LA IXM JUKVB DiCato, CMCTvra !• N» l*-«) LN FL rAia A**<**4*- IJrrnaia del MUMarta A4r«B UN y N«4: Mal W4 d* Gabiema Na. lllll Y«UU«> MW41 Preeto: fM» Tartta FaaUl ■«^aciAa Mk n éa la AMauntolracU* iB^raao M Ultaal^ S*Ul Nvtoaal CalomMa Narra LUa. £/ Gobierno Encubre CQRRÜPCÍQK ADMINISTRATIVA La familia del ministro de Agricultura se enriqueció en seis años, siendo Peñalosa gerente del tncora y ministro,. con la agricultural Sin aclarar "chanchullos * de! ministro y Fadul. — El Incora, un negociado "fabuloso". (Lea página tercera). o MAS (HPtÓM/tnCO TOCOS eo* coetoA....ry Comunistas EXIGEN iRx EIECTDRAEES liA A un año del aplastamiento de la contrarrevolución FI» E.TCKCITO KOJO que aplaiRió al nacUmn. ona tm mU en Chewaiovaqoia, haré nn afio. derrotó la rontrarrevolndón faadsla. cHEcosL ovao uia es Y seevutu stemo sociausTa (LIA PAGINAS 9a. Y lOa.) CJlfW 24 as Acosre km iQ7Q — ÍMCM CL CCNTEN/\tll0 O£L IVACJMÍCJVTQ D£ LCIVrjV — JI970 Jt€t9 9jnuJaHw^ l^niaügH» se r^^Mxó 9D Bui ^aur9 te <*• IsBín M ¡9t BtBéi BVZMtMAJMQK. <1M corra*. Santander, camarada Miguel fio. puiL-.ul juvenil). La juventud co* drigue*. y da un miembro da la munuta de cata dudad realizó dlracciua rarional da la JUCO. MSDELLOf (Del corrwpowal Matfwaaaa y «awirWart. uit gian acto Juvenil político y Los oradorva destacaron la Im- luvenih. En Centro da Ealu'lios tb ■ L. -

Ixe Congrès Européen D'analyse Musicale 9Th European Music
IXe congrès européen d’Analyse musicale 9th European Music Analysis Conference Approches contemporaines ACCRA de la création et de la réflexion artistiques Université de Strasbourg SMA http://euromac2017.unistra.fr The extended abstracts of papers and posters are available on-line on the conference website. The proceedings of EuroMAC 9 will be published on-line after the conference. Graphic design/Conception graphique Jean-Marc CHOUVEL Programme book design/Conception du livret du programme Alexandre FREUND-LEHMANN (supervision) Xavier HASCHER Sandrine BANDURA Nathalie HÉROLD Mathilde BATTAGLIA Laura WALDVOGEL Nerea BERNABEU SEPULCRE Website design/Conception du site Internet : Studio Meta Alexandre FREUND-LEHMANN (supervision) Xavier HASCHER Mathilde BATTAGLIA Nathalie HÉROLD Madeleine LE BOUTEILLER Julie WALKER Nerea BERNABEU SEPULCRE Sandrine BANDURA Laura WALDVOGEL EasyChair system management/Gestion de la plateforme EasyChair Pierre COUPRIE © 2017, LabEx GREAM, 5 allée du Général Rouvillois, 67083 Strasbourg Cedex. Toute reproduction ou représentation de ce programme, intégrale ou partielle, serait illicite sans l’autorisation de l’éditeur et constituerait une contrefaçon. Les cas strictement limités à l’usage privé ou de citation sont régis par la loi du 11 mars 1957. iii Sommaire Un mot de bienvenue v A Word of Welcome vii Ein Willkommensgrußwort ix Benvenuti xi Remerciements xiii Comités xv Programme général 1 Thèmes des sessions préorganisées 23 Programme détaillé et résumés des présentations 41 Annexes 423 Détails pratiques 425 GREAM 429 IReMus 430 Index des auteurs 431 Index des modérateurs 437 Index des autres contributeurs 439 iii Contents Un mot de bienvenue v A Word of Welcome vii Ein Willkommensgrußwort ix Benvenuti xi Many thanks to..