DOCSLIB.ORG

Capacitors and Capacitance

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Capacitors and Capacitance Capacitors and Capacitance Capacitors are devices that can store a charge Q at some voltage V. The greater the capacitance, the more charge that can be stored. The equation for capacitance, C, is very simple: Q ⎡ C ⎤ Q C = ⎢ ⎥ = []F 1F = 1 farad V ⎣V ⎦ V Even an isolated conducting sphere has capacitance. Michael Faraday We just take the equation for the electric potential of a point charge (which also applies to conducting spheres, and find the above ratio: Q kQ Q R R V = C = = R V k Find the capacitance of “Old Sparky” r 0.20m C = = = 22.2×10−12 F = 22.2 pF k 9.00×109 N ⋅ m2 / C2 A capacitance of ~ 20 pF is not very big. If this Van de Graaf generator could reach 1,000,000 V, the total charge on the dome would be only 20 μC. This is one reason this device is safe. The other is that high voltage causes charge to travel along the surface of objects (such as our bodies). The generic capacitor It is more practical to build a conductor out of two conductors, charging them equal and opposite, as an electric dipole. With the right geometry, this will create a “contained” electric field, and the possibility of much larger capacitance than can be achieved with a sphere of equivalent size. Easily calculable capacitor #1: parallel plates Here’s the example we’ve been referring to for some time: the parallel plate capacitor. We assume that the plates are so large compared to their separation d that we can ignore the fringe field, and that all the electric field is inside. Then, as we found earlier, V = Ed. And, since all the charge is on the inner surfaces of the conductors, E = σ /ε0 ‘ Q σA σA ⎛ ε ⎞ ε A This is a simple result. Notice that C C = = = ⎜ 0 ⎟ = 0 V Ed d ⎝ σ ⎠ d depends only on ε0 and the dimensions of the capacitor. We will see the same What happens to C if d thing with all other capacitors. is made very small??? Calculable capacitor #2: concentric spheres This calculation is also easy. We use the equation for the electric potential of a sphere of a given radius and charge. We apply it once to the inner sphere, and again to the outer, to find the voltage difference between the two. (By Gauss’s Law, the only electric field is between the two spheres.) kQ kQ ⎛ r − r ⎞ ⎜ b a ⎟ ΔV = Va −Vb = − = kQ⎜ ⎟ ra rb ⎝ ra rb ⎠ Then, the capacitance of Q 1 ⎛ rarb ⎞ 4πε0rarb a spherical capacitor (in C = = ⎜ ⎟ = vacuum) is: ΔV k ⎝ rb − ra ⎠ rb − ra Calculable capacitor #3: coaxial infinite cylinders We’ve done most of the work already for this, by finding the difference in electric potential at two different radii in a cylindrically symmetric geometry. We simply use that earlier result for ΔV, and find C from the basic equation. ⎛ rb ⎞ ΔV = 2kλ ln⎜ ⎟ ⎝ ra ⎠ Notice that to calculate a Q for the capacitance equation, we need to choose a length, L, so that Q = λL: Capacitance Q λL L C 1 2πε0 C = = = = = per unit length ΔV ⎛ rb ⎞ ⎛ rb ⎞ L ⎛ rb ⎞ ⎛ rb ⎞ 2kλ ln⎜ ⎟ 2k ln⎜ ⎟ 2k ln⎜ ⎟ ln⎜ ⎟ (in vacuum). ⎝ ra ⎠ ⎝ ra ⎠ ⎝ ra ⎠ ⎝ ra ⎠ Popular design for early capacitors – the Leyden Jar In 1745, the Leyden Jar (or Leyden Bottle) was invented by Ewald Jürgen von Kleist (1700-1748). The glass increases the A “Leyden Battery”. What would we capacitance dramatically, as we shall call this configuration today? Again, understand soon … we’ll be discussing this further … Glass Early charging machines Induction machine invented by James Wimshurst c. 1880. The two disks, with narrow tin-foil strips glued around the rim, are rotated in opposite directions by a system of pulleys and belts. At each side there is a conductor, terminating in metal brushes that rub against the tin-foil sectors. The charge is induced in two jaw collectors and stored in a pair of Leyden jars connected to two sliding electrodes. This machine was highly popular and is still used today for teaching purposes. It worked well even in damp weather and did not reverse polarity. Apart from laboratory demonstrations, it was used for medical treatment and as a high-voltage source for the first X-ray tubes. By ~ 1905. Large machines! Modern capacitors: many sizes, shapes, and types http://en.wikipedia.org/wiki/Capacitor http://www.sparkmuseum.com/RADIOS.HTM http://www.uoguelph.ca/~antoon/gadgets/caps/caps.html Capacitor types: (most common types are in red). Metal film: Made from polymer foil with a layer of metal deposited on surface. They have good quality and stability, and are suitable for timer circuits and high frequencies. Mica: Similar to metal film. Often high voltage. Suitable for high frequencies. Paper: Used for high voltages. Glass: Used for high voltages. Stable temperature coefficient in a wide range of temperatures. Ceramic: Chips of altering layers of metal and ceramic. Very common, they find use in low-precision coupling and filtering applications. Good for high frequencies. Electrolytic: Polarized. Similar to metal film in construction, but the electrodes are made of aluminum etched for much higher surface area, and the dielectric is soaked with liquid electrolyte. Can achieve high capacities. Tantalum: Like electrolytic. Polarized. Better performance at higher frequencies. Can tolerate low temperatures. Supercapacitors: Made from carbon aerogel, carbon nanotubes, or highly porous electrode materials. Extremely high capacity. More discussion to come on the subject of dielectrics… Capacitors connected in parallel Consider starting with uncharged capacitors, then connecting a battery across the terminals. What is the total charge in this circuit? Why do the two capacitors have the same voltage, in equilibrium? Use C = Q/V … Solve for the total capacitance of this equivalent circuit, Ceq, in terms of C1 and C2. Å Derive the equation Capacitors connected in series Consider starting with uncharged capacitors, then placing a charge +Q on capacitor C1. Why do the two capacitors have the same charge, in equilibrium? What is the relationship among the voltages? Use C = Q/V … Again, solve for the total capacitance of this “equivalent circuit”, Ceq, in terms of C1 and C2. Å Derive the equation Equations for capacitors connected in parallel and in series Parallel: C = C1 + C2 + ... 1 1 1 Series: = + + ... C C1 C2 Finding the equivalent capacitance of a complex circuit by successive combination of its elements, using the equations we just derived. These circuits are purely capacitive. No resistors, etc. Å Do Potential energy stored in a capacitor We will calculate the work required +Q A to start with a discharged capacitor +++ ++ and charge it to a total charge Q. Imagine we are taking positive V dq d E charge from the lower plate in increments dq and moving them _____ through the voltage difference V -Q created by the electric field. The q 1 Q Q2 work required for this move is qV. U = dW = Vdq = dq = qdq = With each dq that is moved, V ∫ ∫∫ ∫ C C 0 2C increases, so that the work for each dq rises as the capacitor This is the potential energy in any charges. We are describing the charged capacitor since the integration at right, with the final derivation is general! answer being the potential energy For the case of parallel plates: stored in the capacitor. ε A Q2d C = 0 U = d 2ε 0 A General expressions for potential energy in a capacitor, and energy density of the electric field. There are two other forms of the general expression for the potential energy in a capacitor, derivable from the expression on the last page by using V = Q/C to eliminate one of the three variables, V, Q, or C, from the equation: Q2 CV 2 QV U = = = 2C 2 2 Where is the energy stored? Amazingly, in the electric field itself! For the parallel plate capacitor, which has a constant electric field, it is easy to calculate the energy in this field, starting from the second form above: 1 2 1 ⎛ ε 0 A ⎞ 2 1 2 U = CV = ⎜ ⎟(Ed) = ε 0E (Ad) 2 2 ⎝ d ⎠ 2 The factor (Ad) is the volume of this capacitor. If we 1 divide by this factor, the result will be the energy u = ε E 2 density, a general formula that applies (point by point) 2 0 to all electric fields in a vacuum: Charging one capacitor from another: final conditions, and energy. Å Do Why have we been saying “in a vacuum”? If we fill the volume of any capacitor with a “dielectric” material, we will see the following: C0 C For the same charge Q, the voltage on the capacitor in vacuum, V0, will be greater than the voltage, V, on the same capacitor filled with dielectric. Since C = Q/V, the capacitance has been increased by V0 /V. Very useful, but how does this happen? Æ What’s a “dielectric material”? It’s an insulator. And, the property of a dielectric that causes the increase of capacitance is its “polarizability.” There are two classes of dielectrics, with different polarization mechanisms: Polar molecules Non-polar molecules E induces polarization in Partial alignment with E each atom or molecule In both cases, each dipole has an interior electric field that points opposite to the applied field E. So, the total electric field is reduced. Then, since V in a capacitor is the integral of E with distance, V is reduced. The “dielectric constant”, K, is the factor by which C increases: C = KC0 Dielectric constants for various materials: More dielectric constants, plus some “breakdown voltages”: Dielectrics in capacitors: bringing all the physics together First, consider a block of dielectric in an external field E.
Load more

Recommended publications
  • Discovery of Radio Waves 1887 Static Electricity
    Heinrich Hertz (1857 - 1894) Discovery of Radio Waves 1887 Static Electricity • Thales of Miletus (624 – 526 BC) – Two pieces of amber rubbed with wool or two pieces of glass rubbed with silk would repel each other. • We now know that the amber removes electrons from the wool and becomes negatively charged. • Similarly, the glass becomes positively charged, having given up electrons to the silk. – Also, the amber would be attracted to the glass and the wool to the silk. Static Electricity Magnetism • Thales of Miletus (624-526 BCE) • Described the lodestone • China in 100 BCE used the magnetic compass. • By convention, the direction of a magnetic field (S -> N) is indicated by a compass needle. Galileo Galilei (1564 – 1642) • One of the earliest “scientists”, dared to “tinker with nature”, rather than merely observing it. • Observed moons of Jupiter, and supported the Copernican hypothesis. Isaac Newton (1642 – 1727) • Invented calculus to describe gravitation. • Demonstrated that white light is a mixture of colours. • Postulated that light is a stream of corpuscles. • Invented the Newtonian telescope. Static Electricity • 1663 – The earliest friction machines rubbed a glass sphere against wool. • 1733 – Charles Francois du Fay (1698 – 1739) postulated that there were two kinds of electrical fluid – vitreous and resinous Static Electricity • 1733 – The Leyden jar invented in Holland could store charges from generators. • Spurred much research into static electricity. Static Electricity • Benjamin Franklin (1705 - 1790) • 1751 - Lightning was static electricity • Arbitrarily defined Vitreous as “positive” • Resinous, “negative” • Theory of charge conservation Static Electricity • Luigi Galvani (1737–1798) • 1770 - Discovered that static electricity from a Leyden jar could make frog’s legs twitch.
    [Show full text]
  • The Stage Is Set
    The Stage Is Set: Developments before 1900 Leading to Practical Wireless Communication Darrel T. Emerson National Radio Astronomy Observatory1, 949 N. Cherry Avenue, Tucson, AZ 85721 In 1909, Guglielmo Marconi and Carl Ferdinand Braun were awarded the Nobel Prize in Physics "in recognition of their contributions to the development of wireless telegraphy." In the Nobel Prize Presentation Speech by the President of the Royal Swedish Academy of Sciences [1], tribute was first paid to the earlier theorists and experimentalists. “It was Faraday with his unique penetrating power of mind, who first suspected a close connection between the phenomena of light and electricity, and it was Maxwell who transformed his bold concepts and thoughts into mathematical language, and finally, it was Hertz who through his classical experiments showed that the new ideas as to the nature of electricity and light had a real basis in fact.” These and many other scientists set the stage for the rapid development of wireless communication starting in the last decade of the 19th century. I. INTRODUCTION A key factor in the development of wireless communication, as opposed to pure research into the science of electromagnetic waves and phenomena, was simply the motivation to make it work. More than anyone else, Marconi was to provide that. However, for the possibility of wireless communication to be treated as a serious possibility in the first place and for it to be able to develop, there had to be an adequate theoretical and technological background. Electromagnetic theory, itself based on earlier experiment and theory, had to be sufficiently developed that 1.
    [Show full text]
  • Introduction What Is a Polymer Capacitor?
    ECAS series (polymer-type aluminum electrolytic capacitor) No. C2T2CPS-063 Introduction If you take a look at the main board of an electronic device such as a personal computer, you’re likely to see some of the six types of capacitors shown below (Fig. 1). Common types of capacitors include tantalum electrolytic capacitors (MnO2 type and polymer type), aluminum electrolytic capacitors (electrolyte can type, polymer can type, and chip type), and MLCC. Figure 1. Main Types of Capacitors What Is a Polymer Capacitor? There are many other types of capacitors, such as film capacitors and niobium capacitors, but here we will describe polymer capacitors, a type of capacitor produced by Murata among others. In both tantalum electrolytic capacitors and aluminum electrolytic capacitors, a polymer capacitor is a type of electrolytic capacitor in which a conductive polymer is used as the cathode. In a polymer-type aluminum electrolytic capacitor, the anode is made of aluminum foil and the cathode is made of a conductive polymer. In a polymer-type tantalum electrolytic capacitor, the anode is made of the metal tantalum and the cathode is made of a conductive polymer. Figure 2 shows an example of this structure. Figure 2. Example of Structure of Conductive Polymer Aluminum Capacitor In conventional electrolytic capacitors, an electrolyte (electrolytic solution) or manganese dioxide (MnO2) was used as the cathode. Using a conductive polymer instead provides many advantages, making it possible to achieve a lower equivalent series resistance (ESR), more stable thermal characteristics, improved safety, and longer service life. As can be seen in Fig. 1, polymer capacitors have lower ESR than conventional electrolytic Copyright © muRata Manufacturing Co., Ltd.
    [Show full text]
  • Capacitors and Inductors
    DC Principles Study Unit Capacitors and Inductors By Robert Cecci In this text, you’ll learn about how capacitors and inductors operate in DC circuits. As an industrial electrician or elec- tronics technician, you’ll be likely to encounter capacitors and inductors in your everyday work. Capacitors and induc- tors are used in many types of industrial power supplies, Preview Preview motor drive systems, and on most industrial electronics printed circuit boards. When you complete this study unit, you’ll be able to • Explain how a capacitor holds a charge • Describe common types of capacitors • Identify capacitor ratings • Calculate the total capacitance of a circuit containing capacitors connected in series or in parallel • Calculate the time constant of a resistance-capacitance (RC) circuit • Explain how inductors are constructed and describe their rating system • Describe how an inductor can regulate the flow of cur- rent in a DC circuit • Calculate the total inductance of a circuit containing inductors connected in series or parallel • Calculate the time constant of a resistance-inductance (RL) circuit Electronics Workbench is a registered trademark, property of Interactive Image Technologies Ltd. and used with permission. You’ll see the symbol shown above at several locations throughout this study unit. This symbol is the logo of Electronics Workbench, a computer-simulated electronics laboratory. The appearance of this symbol in the text mar- gin signals that there’s an Electronics Workbench lab experiment associated with that section of the text. If your program includes Elec tronics Workbench as a part of your iii learning experience, you’ll receive an experiment lab book that describes your Electronics Workbench assignments.
    [Show full text]
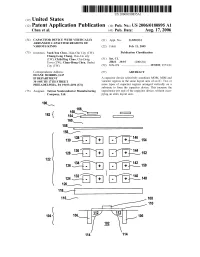
  • 100“ 168\A166\1::: 1:1 162 { 164C 1
    US 20060180895Al (19) United States (12) Patent Application Publication (10) Pub. No.: US 2006/0180895 A1 Chen et al. (43) Pub. Date: Aug. 17, 2006 (54) CAPACITOR DEVICE WITH VERTICALLY (21) Appl. No.: 11/055,933 ARRANGED CAPACITOR REGIONS OF VARIOUS KINDS (22) Filed: Feb. 11, 2005 (75) Inventors: Yueh-You Chen, Hsin-Chu City (TW); Publication Classi?cation Chung-Long Chang, Dou-Liu city (TW); Chih-Ping Chao, Chu-Dong (51) Int. Cl. Town (TW); Chun-Hong Chen, Jhubei H01L 29/93 (2006.01) City (TW) (52) U.S. Cl. .......................................... .. 257/595; 257/E2l Correspondence Address: (57) ABSTRACT DUANE MORRIS, LLP IP DEPARTMENT A capacitor device selectively combines MOM, MIM and 30 SOUTH 17TH STREET varactor regions in the same layout area of an IC. TWo or PHILADELPHIA, PA 19103-4196 (US) more types of capacitor regions arranged vertically on a substrate to form the capacitor device. This increase the (73) Assignee: Taiwan Semiconductor Manufacturing capacitance per unit of the capacitor device, Without occu Company, Ltd. pying an extra layout area. 100“ 168\A166\1::: 1:1 162 { 164C 1:: . 160 158, F I /_\~ ’/'_‘\ 130 Bi- - + - +--E6_,154 /\_ A/A\ 128 i. - + - +--?, 152 122 ' 134 . ,/—\ 142 126 \_/—'—~ . + .. +_-\_, 150 /\'_ ‘/_\ 4 124 i. + - +--—2, 148 120% 118/1- ] 116f 108 112 112 104 10s \ p — /_/ 106 _ m _ 114 l_/114 110 Patent Application Publication Aug. 17, 2006 Sheet 2 0f 2 US 2006/0180895 A1 200“ - + - + + - + - - + - + + - + - FIG. 2 300% 316% + ' + 314“ 312% + + 310v“ ' 308 “w - + - + 306\___ 304“ + + FIG. 3 US 2006/0180895 A1 Aug.
    [Show full text]
  • Capacitor & Capacitance
    CAPACITOR & CAPACITANCE - TYPES Capacitor types Listed by di-electric material. A 12 pF 20 kV fixed vacuum capacitor Vacuum : Two metal, usually copper, electrodes are separated by a vacuum. The insulating envelope is usually glass or ceramic. Typically of low capacitance - 10 - 1000 pF and high voltage, up to tens of kilovolts, they are most often used in radio transmitters and other high voltage power devices. Both fixed and variable types are available. Vacuum variable capacitors can have a minimum to maximum capacitance ratio of up to 100, allowing any tuned circuit to cover a full decade of frequency. Vacuum is the most perfect of dielectrics with a zero loss tangent. This allows very high powers to be transmitted without significant loss and consequent heating. Air : Air dielectric capacitors consist of metal plates separated by an air gap. The metal plates, of which there may be many interleaved, are most often made of aluminium or silver-plated brass. Nearly all air dielectric capacitors are variable and are used in radio tuning circuits. Metallized plastic film: Made from high quality polymer film (usually polycarbonate, polystyrene, polypropylene, polyester (Mylar), and for high quality capacitors polysulfone), and metal foil or a layer of metal deposited on surface. They have good quality and stability, and are suitable for timer circuits. Suitable for high frequencies. Mica: Similar to metal film. Often high voltage. Suitable for high frequencies. Expensive. Excellent tolerance. Paper: Used for relatively high voltages. Now obsolete. Glass: Used for high voltages. Expensive. Stable temperature coefficient in a wide range of temperatures. Ceramic: Chips of alternating layers of metal and ceramic.
    [Show full text]
  • 3. PPE Materials Components and Devices 2019 USPAS
    Pulsed Power Engineering: Materials & Passive Components and Devices U.S. Particle Accelerator School University of New Mexico Craig Burkhart & Mark Kemp SLAC National Accelerator Laboratory June 24-28, 2019 Materials & Passive Components and Devices Used in Pulsed Power Engineering - Materials • Conductors • Insulators • Magnetic material - Passive components and devices • Resistors • Capacitors • Inductors • Transformers • Transmission lines • Loads - Klystrons - Beam kickers Jun. 24-28, 2019 USPAS Pulsed Power Engineering C. Burkhart & M. Kemp 2 Materials - Generally encounter three types of materials in pulsed power work • Conductors - Wires & cable - Buss bars - Shielding - Resistors • Insulators - Cables and bushing - Standoffs - Capacitors • Magnetic - Inductors, transformers, and magnetic switches - Ferrite and tape-wound Jun. 24-28, 2019 USPAS Pulsed Power Engineering C. Burkhart & M. Kemp 3 Calculating Resistance - At low frequency, resistance (R) determined by: • R = ρℓ/A (ohm) - Material resistivity, ρ (Ω•cm) - Conductor length, ℓ (cm) - Conductor cross-sectional area, A (cm2) - At high frequency, effective conductor area decreased by “skin effect” • Conducted current produces magnetic field • Magnetic field induces eddy currents in conductor which oppose/cancel B • Eddy currents decay due to material resistance, allow conducted current/magnetic field to penetrate material • Skin depth, δ, is the effective conducted current penetration (B = Bapplied/e) • δ = (2ρ/μω)½ (meters) for a current of a fixed frequency ω=2πf, or δ ≈ (2tρ/μ)½ (meters) for a pulsed current of duration t (sec) - Material resistivity, ρ (Ω•m) - Material permeability, μ (H/m) ½ ½ • δ = (6.6/f )[(ρ/ρc)/(μ/μo)] (cm) -8 - Normalized resistivity, (ρ/ρc) , copper resistivity, ρc = 1.7 X 10 (Ω•m) -7 - Relative permeability, μr =(μ/μo), permeability of free space, μo = 4π X 10 (H/m) • Litz wire is woven to minimize skin effects Jun.
    [Show full text]
  • Leyden Jars and Batteries According to Benjamin Franklin
    eRittenhouse The Art of Making Leyden Jars and Batteries According to Benjamin Franklin Sara J. Schechner David P. Wheatland Curator of the Collection of Historical Scientific Instruments Department of the History of Science, Harvard University [email protected] Abstract The Leyden jar was arguably the most important instrument for electrical experiments in the second half of the 18th century, and Benjamin Franklin’s fame as a natural philosopher was based largely on his explanation of how it worked. In two remarkable letters written in the 1750s to scholars in Boston, Franklin offers instruction on the making of Leyden jars and assembling them into batteries. The letters also illustrate the challenges of getting and maintaining natural philosophical apparatus in colonial America, and a culture of recycling goods in order to make do. In the 1750s, Benjamin Franklin sent supplies and instructions for making Leyden jars to James Bowdoin, a Boston merchant and statesman interested in natural philosophy,1 and to John Winthrop, Hollis Professor of Mathematics and Natural Philosophy at Harvard College. Given the importance of Leyden jars to the development of Franklin’s own electrical theory, we are curious to know how Franklin made his own and what his recommendations might have been. The letters also illustrate the culture of repurposing goods and bricolage that was part of early modern science, particularly in the American colonies.2 1 James Bowdoin (1726-1790) was elected to the Massachusetts House of Representatives in 1753 and in 1757 began decades of service in the Council. His later leadership positions included governorship of the Commonwealth of Massachusetts in 1785-1787.
    [Show full text]
  • Lesson 04 Capacitors Inductors Antennas
    Sierra College CIE-01 Jim Weir 530.272.2203 Lesson 04 [email protected] www.rstengineering.com/sierra Capacitors Inductors Antennas Capacitors A capacitor is two conductors separated by an insulator. That's pretty generic, isn't it? For example, you are a salt water sack (conductor) separated from your lab partner by an insulator (air). Does that make you two a capacitor? You bet. How about your automobile (steel) separated from the earth (conductor) by rubber tires? Yup (anybody old enough to remember "grounding straps"?). How about the earth and the moon separated by space? You bet. Going to the other extreme, how about two copper atoms separated by the "nothingness" of a billionth of an inch inside the copper molecule? You got it. One of the first capacitors was the Leyden jar, so named because it was invented by Pieter van Musschenbroek of the University of Leyden, Netherlands in 1745. It consisted of an outer metal shell, a glass jar, and an inner metal plate. Two brass conductors separated by a glass insulator. Because at the time it was thought to "condense" the "vapors of electricity" into a jar, it was originally called a "condenser", a name that was used for this electrical device up until the 1950s when the modern word capacitor became the preferred nomenclature. Page 1 of 16 Benjamin Franklin (late, of Philadelphia) did some experimentation with atmospheric static electricity. Franklin used the static electricity to first attract the small pith ball to the Leyden jar's "bell", and then after it was charged, it was repelled to the "grounding" bell, then reattracted to the jar bell, and so on until the static charge was dissipated.
    [Show full text]
  • MT-101: Decoupling Techniques
    MT-101 TUTORIAL Decoupling Techniques WHAT IS PROPER DECOUPLING AND WHY IS IT NECESSARY? Most ICs suffer performance degradation of some type if there is ripple and/or noise on the power supply pins. A digital IC will incur a reduction in its noise margin and a possible increase in clock jitter. For high performance digital ICs, such as microprocessors and FPGAs, the specified tolerance on the supply (±5%, for example) includes the sum of the dc error, ripple, and noise. The digital device will meet specifications if this voltage remains within the tolerance. The traditional way to specify the sensitivity of an analog IC to power supply variations is the power supply rejection ratio (PSRR). For an amplifier, PSRR is the ratio of the change in output voltage to the change in power supply voltage, expressed as a ratio (PSRR) or in dB (PSR). PSRR can be referred to the output (RTO) or referred to the input (RTI). The RTI value is equal to the RTO value divided by the gain of the amplifier. Figure 1 shows how the PSR of a typical high performance amplifier (AD8099) degrades with frequency at approximately 6 dB/octave (20 dB/decade). Curves are shown for both the positive and negative supply. Although 90 dB at dc, the PSR drops rapidly at higher frequencies where more and more unwanted energy on the power line will couple to the output directly. Therefore, it is necessary to keep this high frequency energy from entering the chip in the first place. This is generally done with a combination of electrolytic capacitors (for low frequency decoupling), ceramic capacitors (for high frequency decoupling), and possibly ferrite beads.
    [Show full text]
  • Wei Thesis.Pdf
    UNIVERSITY OF CALIFORNIA Santa Barbara Wide Bandwidth Power Heterojunction Bipolar Transistors and Amplifiers A Dissertation submitted in partial satisfaction of the requirements for the degree Doctor of Philosophy in Electrical and Computer Engineering by Yun Wei Committee in charge: Professor Mark Rodwell, Chair Professor Steve Long Professor Umesh Mishra Professor Robert York March, 2003 The dissertation of Yun Wei is approved. _____________________________________________ Professor Steve Long _____________________________________________ Professor Umesh Mishra _____________________________________________ Professor Robert York _____________________________________________ Professor Mark Rodwell, Committee Chair November, 2002 ii Wide Bandwidth Power Heterojunction Bipolar Transistors and Amplifiers Copyright © 2003 by Yun Wei iii To my wife and daughter. iv ACKNOWLEDGEMENTS I would like to say that I feel lucky of being a student of Prof. Rodwell. I am always indebted to him for his advice and assistance during my graduate school career. I have learned not only the knowledge, but also gained a lot from his enthusiasm for scientific research and willingness to help others. I would also like to thank my committee members Prof. Umesh Mishra, Prof. Stephen Long and Prof. Robert York for their patience, encouragement and support. It was my greatest pleasure of working with my colleagues, who gave me both helps and friendliness. Thanks to Dino, James, Shri, Tomas and PK, who gave me the first laboratory training. Special thanks to Paidi, Miguel and Dennis; this thesis would not have been possible without their contributions. Also thanks to Sangmin, Zach, Shouxuan, Mattias, and Navin for their suggestions and support during this work. The excellent support received from Jack Whaley, Mike Anzlowar, Bob Hill, and Neil Baker led to the successful fabrication of the devices and MMICs described in this work.
    [Show full text]
  • 01. Franklin Intro 9/04
    Franklin and Electrostatics- Ben Franklin as my Lab Partner A Workshop on Franklin’s Experiments in Electrostatics Developed at the Wright Center for Innovative Science Teaching Tufts University Medford MA 02155 by Robert A. Morse, Ph.D. ©2004 Sept 2004 Benjamin Franklin observing his lightning alarm. Described in Section VII. Engraving after the painting by Mason Chamberlin, R. A. Reproduced from Bigelow, 1904 Vol. VII Franklin and Electrostatics version 1.3 ©2004 Robert A. Morse Wright Center for Science Teaching, Tufts University Section I- page 1 Copyright and reproduction Copyright 2004 by Robert A. Morse, Wright Center for Science Education, Tufts University, Medford, MA. Quotes from Franklin and others are in the public domain, as are images labeled public domain. These materials may be reproduced freely for educational and individual use and extracts may be used with acknowledgement and a copy of this notice.These materials may not be reproduced for commercial use or otherwise sold without permission from the copyright holder. The materials are available on the Wright Center website at www.tufts.edu/as/wright_center/ Acknowledgements Rodney LaBrecque, then at Milton Academy, wrote a set of laboratory activities on Benjamin Franklin’s experiments, which was published as an appendix to my 1992 book, Teaching about Electrostatics, and I thank him for directing my attention to Franklin’s writing and the possibility of using his experiments in teaching. I would like to thank the Fondation H. Dudley Wright and the Wright Center for Innovative Science Teaching at Tufts University for the fellowship support and facilities that made this work possible.
    [Show full text]