Nuclear Physics Exploring the Heart of Matter
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

B2.IV Nuclear and Particle Physics
B2.IV Nuclear and Particle Physics A.J. Barr February 13, 2014 ii Contents 1 Introduction 1 2 Nuclear 3 2.1 Structure of matter and energy scales . 3 2.2 Binding Energy . 4 2.2.1 Semi-empirical mass formula . 4 2.3 Decays and reactions . 8 2.3.1 Alpha Decays . 10 2.3.2 Beta decays . 13 2.4 Nuclear Scattering . 18 2.4.1 Cross sections . 18 2.4.2 Resonances and the Breit-Wigner formula . 19 2.4.3 Nuclear scattering and form factors . 22 2.5 Key points . 24 Appendices 25 2.A Natural units . 25 2.B Tools . 26 2.B.1 Decays and the Fermi Golden Rule . 26 2.B.2 Density of states . 26 2.B.3 Fermi G.R. example . 27 2.B.4 Lifetimes and decays . 27 2.B.5 The flux factor . 28 2.B.6 Luminosity . 28 2.C Shell Model § ............................. 29 2.D Gamma decays § ............................ 29 3 Hadrons 33 3.1 Introduction . 33 3.1.1 Pions . 33 3.1.2 Baryon number conservation . 34 3.1.3 Delta baryons . 35 3.2 Linear Accelerators . 36 iii CONTENTS CONTENTS 3.3 Symmetries . 36 3.3.1 Baryons . 37 3.3.2 Mesons . 37 3.3.3 Quark flow diagrams . 38 3.3.4 Strangeness . 39 3.3.5 Pseudoscalar octet . 40 3.3.6 Baryon octet . 40 3.4 Colour . 41 3.5 Heavier quarks . 43 3.6 Charmonium . 45 3.7 Hadron decays . 47 Appendices 48 3.A Isospin § ................................ 49 3.B Discovery of the Omega § ...................... -

Electron-Nucleon Scattering at LDMX for DUNE
Snowmass Letter of Intent: Snowmass Topical Groups: NF6, RF6, TF11 Electron-Nucleon Scattering at LDMX for DUNE Torsten Akesson1, Artur Ankowski2, Nikita Blinov3, Lene Kristian Bryngemark4, Pierfrancesco Butti2, Caterina Doglioni1, Craig Dukes5, Valentina Dutta6, Bertrand Echenard7, Thomas Eichlersmith8, Ralf Ehrlich5, Andrew Furmanski∗8, Niramay Gogate9, Mathew Graham2, Craig Group5, Alexander Friedland2, David Hitlin7, Vinay Hegde9, Christian Herwig3, Joseph Incandela6, Wesley Ketchumy3, Gordan Krnjaic3, Amina Li6, Shirley Liz2,3, Dexu Lin7, Jeremiah Mans8, Cristina Mantilla Suarez3, Phillip Masterson6, Martin Meier8, Sophie Middleton7, Omar Moreno2, Geoffrey Mullier1, Tim Nelson2, James Oyang7, Gianluca Petrillo2, Ruth Pottgen1, Stefan Prestel1, Luis Sarmiento1, Philip Schuster2, Hirohisa Tanaka2, Lauren Tompkins4, Natalia Toro2, Nhan Tran§3, and Andrew Whitbeck9 1Lund University 2Stanford Linear Accelerator Laboratory 3Fermi National Accelerator Laboratory 4Stanford University 5University of Virginia 6University of California Santa Barbara 7California Institute of Technology 8University of Minnesota 9Texas Tech University ABSTRACT We point out that the LDMX (Light Dark Matter eXperiment) detector design, conceived to search for sub-GeV dark matter, will also have very advantageous characteristics to pursue electron-nucleus scattering measurements of direct relevance to the neutrino program at DUNE and elsewhere. These characteristics include a 4-GeV electron beam, a precision tracker, electromagnetic and hadronic calorimeters with near 2p azimuthal acceptance from the forward beam axis out to 40◦ angle, and low reconstruction energy threshold. LDMX thus could provide (semi)exclusive cross section measurements, with∼ detailed information about final-state electrons, pions, protons, and neutrons. We compare the predictions of two widely used neutrino generators (GENIE, GiBUU) in the LDMX region of acceptance to illustrate the large modeling discrepancies in electron-nucleus interactions at DUNE-like kinematics. -
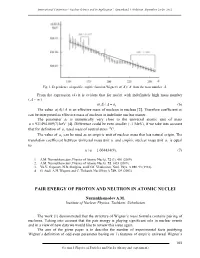
Pair Energy of Proton and Neutron in Atomic Nuclei
International Conference “Nuclear Science and its Application”, Samarkand, Uzbekistan, September 25-28, 2012 Fig. 1. Dependence of specific empiric function Wigner's a()/ A A from the mass number A. From the expression (4) it is evident that for nuclei with indefinitely high mass number ( A ~ ) a()/. A A a1 (6) The value a()/ A A is an effective mass of nucleon in nucleus [2]. Therefore coefficient a1 can be interpreted as effective mass of nucleon in indefinite nuclear matter. The parameter a1 is numerically very close to the universal atomic unit of mass u 931494.009(7) keV [4]. Difference could be even smaller (~1 MeV), if we take into account that for definition of u, used mass of neutral atom 12C. The value of a1 can be used as an empiric unit of nuclear mass that has natural origin. The translation coefficient between universal mass unit u and empiric nuclear mass unit a1 is equal to: u/ a1 1.004434(9). (7) 1. A.M. Nurmukhamedov, Physics of Atomic Nuclei, 72 (3), 401 (2009). 2. A.M. Nurmukhamedov, Physics of Atomic Nuclei, 72, 1435 (2009). 3. Yu.V. Gaponov, N.B. Shulgina, and D.M. Vladimirov, Nucl. Phys. A 391, 93 (1982). 4. G. Audi, A.H. Wapstra and C. Thibault, Nucl.Phys A 729, 129 (2003). PAIR ENERGY OF PROTON AND NEUTRON IN ATOMIC NUCLEI Nurmukhamedov A.M. Institute of Nuclear Physics, Tashkent, Uzbekistan The work [1] demonstrated that the structure of Wigner’s mass formula contains pairing of nucleons. Taking into account that the pair energy is playing significant role in nuclear events and in a view of new data we would like to review this issue again. -

From Quark and Nucleon Correlations to Discrete Symmetry and Clustering
From quark and nucleon correlations to discrete symmetry and clustering in nuclei G. Musulmanbekov JINR, Dubna, RU-141980, Russia E-mail: [email protected] Abstract Starting with a quark model of nucleon structure in which the valence quarks are strongly correlated within a nucleon, the light nu- clei are constructed by assuming similar correlations of the quarks of neighboring nucleons. Applying the model to larger collections of nucleons reveals the emergence of the face-centered cubic (FCC) sym- metry at the nuclear level. Nuclei with closed shells possess octahedral symmetry. Binding of nucleons are provided by quark loops formed by three and four nucleon correlations. Quark loops are responsible for formation of exotic (borromean) nuclei, as well. The model unifies independent particle (shell) model, liquid-drop and cluster models. 1 Introduction arXiv:1708.04437v2 [nucl-th] 19 Sep 2017 Historically there are three well known conventional nuclear models based on different assumption about the phase state of the nucleus: the liquid-drop, shell (independent particle), and cluster models. The liquid-drop model re- quires a dense liquid nuclear interior (short mean-free-path, local nucleon interactions and space-occupying nucleons) in order to predict nuclear bind- ing energies, radii, collective oscillations, etc. In contrast, in the shell model each point nucleon moves in mean-field potential created by other nucleons; the model predicts the existence of nucleon orbitals and shell-like orbital- filling. The cluster models require the assumption of strong local-clustering 1 of particularly the 4-nucleon alpha-particle within a liquid or gaseous nuclear interior in order to make predictions about the ground and excited states of cluster configurations. -

First Results of the Cosmic Ray NUCLEON Experiment
Prepared for submission to JCAP First results of the cosmic ray NUCLEON experiment E. Atkin,a V. Bulatov,b V. Dorokhov,b N. Gorbunov,c;d S. Filippov,b V. Grebenyuk,c;d D. Karmanov,e I. Kovalev,e I. Kudryashov,e A. Kurganov,e M. Merkin,e A. Panov,e;1 D. Podorozhny,e D. Polkov,b S. Porokhovoy,c V. Shumikhin,a L. Sveshnikova,e A. Tkachenko,c;f L. Tkachev,c;d A. Turundaevskiy,e O. Vasiliev ande A. Voronine aNational Research Nuclear University “MEPhI”, Kashirskoe highway, 31. Moscow, 115409, Russia bSDB Automatika, Mamin-Sibiryak str, 145, Ekaterinburg, 620075, Russia cJoint Institute for Nuclear Research, Dubna, Joliot-Curie, 6, Moscow region, 141980, Russia d arXiv:1702.02352v2 [astro-ph.HE] 2 Jul 2018 “DUBNA” University, Universitetskaya str., 19, Dubna, Moscow region, 141980, Russia eSkobeltsyn Institute of Nuclear Physics, Moscow State University, 1(2), Leninskie gory, GSP-1, Moscow, 119991, Russia f Bogolyubov Institute for Theoretical Physics, 14-b Metrolohichna str., Kiev, 03143, Ukraine 1Corresponding author. E-mail: [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], [email protected], tfl[email protected], [email protected], [email protected], [email protected], [email protected], [email protected] Abstract. -

14. Structure of Nuclei Particle and Nuclear Physics
14. Structure of Nuclei Particle and Nuclear Physics Dr. Tina Potter Dr. Tina Potter 14. Structure of Nuclei 1 In this section... Magic Numbers The Nuclear Shell Model Excited States Dr. Tina Potter 14. Structure of Nuclei 2 Magic Numbers Magic Numbers = 2; 8; 20; 28; 50; 82; 126... Nuclei with a magic number of Z and/or N are particularly stable, e.g. Binding energy per nucleon is large for magic numbers Doubly magic nuclei are especially stable. Dr. Tina Potter 14. Structure of Nuclei 3 Magic Numbers Other notable behaviour includes Greater abundance of isotopes and isotones for magic numbers e.g. Z = 20 has6 stable isotopes (average=2) Z = 50 has 10 stable isotopes (average=4) Odd A nuclei have small quadrupole moments when magic First excited states for magic nuclei higher than neighbours Large energy release in α, β decay when the daughter nucleus is magic Spontaneous neutron emitters have N = magic + 1 Nuclear radius shows only small change with Z, N at magic numbers. etc... etc... Dr. Tina Potter 14. Structure of Nuclei 4 Magic Numbers Analogy with atomic behaviour as electron shells fill. Atomic case - reminder Electrons move independently in central potential V (r) ∼ 1=r (Coulomb field of nucleus). Shells filled progressively according to Pauli exclusion principle. Chemical properties of an atom defined by valence (unpaired) electrons. Energy levels can be obtained (to first order) by solving Schr¨odinger equation for central potential. 1 E = n = principle quantum number n n2 Shell closure gives noble gas atoms. Are magic nuclei analogous to the noble gas atoms? Dr. -

Electron- Vs Neutrino-Nucleus Scattering
Electron- vs Neutrino-Nucleus Scattering Omar Benhar INFN and Department of Physics Universita` “La Sapienza” I-00185 Roma, Italy NUFACT11 University of Geneva, August 2nd, 2011 Neutrino-nucleus scattering . impact of the flux average . flux-averaged electron scattering x-section: a numerical experiment . contributions of reaction mechanisms other than quasi elastic single nucleon knock out to the MiniBooNE CCQE data sample Summary & Outlook Outline Electron scattering . standard data representation . theoretical description: the impulse approximation Omar Benhar (INFN, Roma) NUFACT11 Geneva 02/08/2011 2 / 24 Summary & Outlook Outline Electron scattering . standard data representation . theoretical description: the impulse approximation Neutrino-nucleus scattering . impact of the flux average . flux-averaged electron scattering x-section: a numerical experiment . contributions of reaction mechanisms other than quasi elastic single nucleon knock out to the MiniBooNE CCQE data sample Omar Benhar (INFN, Roma) NUFACT11 Geneva 02/08/2011 2 / 24 Outline Electron scattering . standard data representation . theoretical description: the impulse approximation Neutrino-nucleus scattering . impact of the flux average . flux-averaged electron scattering x-section: a numerical experiment . contributions of reaction mechanisms other than quasi elastic single nucleon knock out to the MiniBooNE CCQE data sample Summary & Outlook Omar Benhar (INFN, Roma) NUFACT11 Geneva 02/08/2011 2 / 24 The inclusive electron-nucleus x-section The x-section of the process e -

Prospects for Measurements with Strange Hadrons at Lhcb
Prospects for measurements with strange hadrons at LHCb A. A. Alves Junior1, M. O. Bettler2, A. Brea Rodr´ıguez1, A. Casais Vidal1, V. Chobanova1, X. Cid Vidal1, A. Contu3, G. D'Ambrosio4, J. Dalseno1, F. Dettori5, V.V. Gligorov6, G. Graziani7, D. Guadagnoli8, T. Kitahara9;10, C. Lazzeroni11, M. Lucio Mart´ınez1, M. Moulson12, C. Mar´ınBenito13, J. Mart´ınCamalich14;15, D. Mart´ınezSantos1, J. Prisciandaro 1, A. Puig Navarro16, M. Ramos Pernas1, V. Renaudin13, A. Sergi11, K. A. Zarebski11 1Instituto Galego de F´ısica de Altas Enerx´ıas(IGFAE), Santiago de Compostela, Spain 2Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom 3INFN Sezione di Cagliari, Cagliari, Italy 4INFN Sezione di Napoli, Napoli, Italy 5Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom, now at Universit`adegli Studi di Cagliari, Cagliari, Italy 6LPNHE, Sorbonne Universit´e,Universit´eParis Diderot, CNRS/IN2P3, Paris, France 7INFN Sezione di Firenze, Firenze, Italy 8Laboratoire d'Annecy-le-Vieux de Physique Th´eorique , Annecy Cedex, France 9Institute for Theoretical Particle Physics (TTP), Karlsruhe Institute of Technology, Kalsruhe, Germany 10Institute for Nuclear Physics (IKP), Karlsruhe Institute of Technology, Kalsruhe, Germany 11School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom 12INFN Laboratori Nazionali di Frascati, Frascati, Italy 13Laboratoire de l'Accelerateur Lineaire (LAL), Orsay, France 14Instituto de Astrof´ısica de Canarias and Universidad de La Laguna, Departamento de Astrof´ısica, La Laguna, Tenerife, Spain 15CERN, CH-1211, Geneva 23, Switzerland 16Physik-Institut, Universit¨atZ¨urich,Z¨urich,Switzerland arXiv:1808.03477v2 [hep-ex] 31 Jul 2019 Abstract This report details the capabilities of LHCb and its upgrades towards the study of kaons and hyperons. -

In-Medium QCD Sum Rules for Ω Meson, Nucleon and D Meson QCD-Summenregeln F ¨Ur Im Medium Modifizierte Ω-Mesonen, Nukleonen Und D-Mesonen
Institut f¨ur Theoretische Physik Fakult¨at Mathematik und Naturwissenschaften Technische Universit¨at Dresden In-Medium QCD Sum Rules for ω Meson, Nucleon and D Meson QCD-Summenregeln f ¨ur im Medium modifizierte ω-Mesonen, Nukleonen und D-Mesonen Dissertation zur Erlangung des akademischen Grades Doctor rerum naturalium vorgelegt von Ronny Thomas geboren am 7. Februar 1978 in Dresden C Dresden 2008 To Andrea and Maximilian Eingereicht am 07. Oktober 2008 1. Gutachter: Prof. Dr. Burkhard K¨ampfer 2. Gutachter: Prof. Dr. Christian Fuchs 3. Gutachter: PD Dr. Stefan Leupold Verteidigt am 28. Januar 2009 Abstract The modifications of hadronic properties caused by an ambient nuclear medium are investigated within the scope of QCD sum rules. This is exemplified for the cases of the ω meson, the nucleon and the D meson. By virtue of the sum rules, integrated spectral densities of these hadrons are linked to properties of the QCD ground state, quantified in condensates. For the cases of the ω meson and the nucleon it is discussed how the sum rules allow a restriction of the parameter range of poorly known four-quark condensates by a comparison of experimental and theoretical knowledge. The catalog of independent four-quark condensates is covered and relations among these condensates are revealed. The behavior of four-quark condensates under the chiral symmetry group and the relation to order parameters of spontaneous chiral symmetry breaking are outlined. In this respect, also the QCD condensates appearing in differences of sum rules of chiral partners are investigated. Finally, the effects of an ambient nuclear medium on the D meson are discussed and relevant condensates are identified. -

Dark Matter in Nuclear Physics
Dark Matter in Nuclear Physics George Fuller (UCSD), Andrew Hime (LANL), Reyco Henning (UNC), Darin Kinion (LLNL), Spencer Klein (LBNL), Stefano Profumo (Caltech) Michael Ramsey-Musolf (Caltech/UW Madison), Robert Stokstad (LBNL) Introduction A transcendent accomplishment of nuclear physics and observational cosmology has been the definitive measurement of the baryon content of the universe. Big Bang Nucleosynthesis calculations, combined with measurements made with the largest new telescopes of the primordial deuterium abundance, have inferred the baryon density of the universe. This result has been confirmed by observations of the anisotropies in the Cosmic Microwave Background. The surprising upshot is that baryons account for only a small fraction of the observed mass and energy in the universe. It is now firmly established that most of the mass-energy in the Universe is comprised of non-luminous and unknown forms. One component of this is the so- called “dark energy”, believed to be responsible for the observed acceleration of the expansion rate of the universe. Another component appears to be composed of non-luminous material with non-relativistic kinematics at the current epoch. The relationship between the dark matter and the dark energy is unknown. Several national studies and task-force reports have found that the identification of the mysterious “dark matter” is one of the most important pursuits in modern science. It is now clear that an explanation for this phenomenon will require some sort of new physics, likely involving a new particle or particles, and in any case involving physics beyond the Standard Model. A large number of dark matter studies, from theory to direct dark matter particle detection, involve nuclear physics and nuclear physicists. -

Lepton Probes in Nuclear Physics
L C f' - l ■) aboratoire ATIONAI FR9601644 ATURNE 91191 Gif-sur-Yvette Cedex France LEPTON PROBES IN NUCLEAR PHYSICS J. ARVIEUX Laboratoire National Saturne IN2P3-CNRS A DSM-CEA, CESaclay F-9I191 Gif-sur-Yvette Cedex, France EPS Conference : Large Facilities in Physics, Lausanne (Switzerland) Sept. 12-14, 1994 ££)\-LNS/Ph/94-18 Centre National de la Recherche Scientifique CBD Commissariat a I’Energie Atomique VOL LEPTON PROBES IN NUCLEAR PHYSICS J. ARVTEUX Laboratoire National Saturne IN2P3-CNRS &. DSM-CEA, CESaclay F-91191 Gif-sur-Yvette Cedex, France ABSTRACT 1. Introduction This review concerns the facilities which use the lepton probe to learn about nuclear physics. Since this Conference is attended by a large audience coming from diverse horizons, a few definitions may help to explain what I am going to talk about. 1.1. Leptons versus hadrons The particle physics world is divided in leptons and hadrons. Leptons are truly fundamental particles which are point-like (their dimension cannot be measured) and which interact with matter through two well-known forces : the electromagnetic interaction and the weak interaction which have been regrouped in the 70's in the single electroweak interaction following the theoretical insight of S. Weinberg (Nobel prize in 1979) and the experimental discoveries of the Z° and W±- bosons at CERN by C. Rubbia and Collaborators (Nobel prize in 1984). The leptons comprise 3 families : electrons (e), muons (jt) and tau (r) and their corresponding neutrinos : ve, and vr . Nuclear physics can make use of electrons and muons but since muons are produced at large energy accelerators, they more or less belong to the particle world although they can also be used to study solid state physics. -

The Nuclear Physics of Neutron Stars
The Nuclear Physics of Neutron Stars Exotic Beam Summer School 2015 Florida State University Tallahassee, FL - August 2015 J. Piekarewicz (FSU) Neutron Stars EBSS 2015 1 / 21 My FSU Collaborators My Outside Collaborators Genaro Toledo-Sanchez B. Agrawal (Saha Inst.) Karim Hasnaoui M. Centelles (U. Barcelona) Bonnie Todd-Rutel G. Colò (U. Milano) Brad Futch C.J. Horowitz (Indiana U.) Jutri Taruna W. Nazarewicz (MSU) Farrukh Fattoyev N. Paar (U. Zagreb) Wei-Chia Chen M.A. Pérez-Garcia (U. Raditya Utama Salamanca) P.G.- Reinhard (U. Erlangen-Nürnberg) X. Roca-Maza (U. Milano) D. Vretenar (U. Zagreb) J. Piekarewicz (FSU) Neutron Stars EBSS 2015 2 / 21 S. Chandrasekhar and X-Ray Chandra White dwarfs resist gravitational collapse through electron degeneracy pressure rather than thermal pressure (Dirac and R.H. Fowler 1926) During his travel to graduate school at Cambridge under Fowler, Chandra works out the physics of the relativistic degenerate electron gas in white dwarf stars (at the age of 19!) For masses in excess of M =1:4 M electrons becomes relativistic and the degeneracy pressure is insufficient to balance the star’s gravitational attraction (P n5=3 n4=3) ∼ ! “For a star of small mass the white-dwarf stage is an initial step towards complete extinction. A star of large mass cannot pass into the white-dwarf stage and one is left speculating on other possibilities” (S. Chandrasekhar 1931) Arthur Eddington (1919 bending of light) publicly ridiculed Chandra’s on his discovery Awarded the Nobel Prize in Physics (in 1983 with W.A. Fowler) In 1999, NASA lunches “Chandra” the premier USA X-ray observatory J.