S Ince the Brilliant Insights and Pioneering
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

B2.IV Nuclear and Particle Physics
B2.IV Nuclear and Particle Physics A.J. Barr February 13, 2014 ii Contents 1 Introduction 1 2 Nuclear 3 2.1 Structure of matter and energy scales . 3 2.2 Binding Energy . 4 2.2.1 Semi-empirical mass formula . 4 2.3 Decays and reactions . 8 2.3.1 Alpha Decays . 10 2.3.2 Beta decays . 13 2.4 Nuclear Scattering . 18 2.4.1 Cross sections . 18 2.4.2 Resonances and the Breit-Wigner formula . 19 2.4.3 Nuclear scattering and form factors . 22 2.5 Key points . 24 Appendices 25 2.A Natural units . 25 2.B Tools . 26 2.B.1 Decays and the Fermi Golden Rule . 26 2.B.2 Density of states . 26 2.B.3 Fermi G.R. example . 27 2.B.4 Lifetimes and decays . 27 2.B.5 The flux factor . 28 2.B.6 Luminosity . 28 2.C Shell Model § ............................. 29 2.D Gamma decays § ............................ 29 3 Hadrons 33 3.1 Introduction . 33 3.1.1 Pions . 33 3.1.2 Baryon number conservation . 34 3.1.3 Delta baryons . 35 3.2 Linear Accelerators . 36 iii CONTENTS CONTENTS 3.3 Symmetries . 36 3.3.1 Baryons . 37 3.3.2 Mesons . 37 3.3.3 Quark flow diagrams . 38 3.3.4 Strangeness . 39 3.3.5 Pseudoscalar octet . 40 3.3.6 Baryon octet . 40 3.4 Colour . 41 3.5 Heavier quarks . 43 3.6 Charmonium . 45 3.7 Hadron decays . 47 Appendices 48 3.A Isospin § ................................ 49 3.B Discovery of the Omega § ...................... -
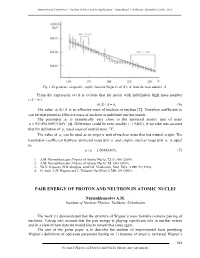
Pair Energy of Proton and Neutron in Atomic Nuclei
International Conference “Nuclear Science and its Application”, Samarkand, Uzbekistan, September 25-28, 2012 Fig. 1. Dependence of specific empiric function Wigner's a()/ A A from the mass number A. From the expression (4) it is evident that for nuclei with indefinitely high mass number ( A ~ ) a()/. A A a1 (6) The value a()/ A A is an effective mass of nucleon in nucleus [2]. Therefore coefficient a1 can be interpreted as effective mass of nucleon in indefinite nuclear matter. The parameter a1 is numerically very close to the universal atomic unit of mass u 931494.009(7) keV [4]. Difference could be even smaller (~1 MeV), if we take into account that for definition of u, used mass of neutral atom 12C. The value of a1 can be used as an empiric unit of nuclear mass that has natural origin. The translation coefficient between universal mass unit u and empiric nuclear mass unit a1 is equal to: u/ a1 1.004434(9). (7) 1. A.M. Nurmukhamedov, Physics of Atomic Nuclei, 72 (3), 401 (2009). 2. A.M. Nurmukhamedov, Physics of Atomic Nuclei, 72, 1435 (2009). 3. Yu.V. Gaponov, N.B. Shulgina, and D.M. Vladimirov, Nucl. Phys. A 391, 93 (1982). 4. G. Audi, A.H. Wapstra and C. Thibault, Nucl.Phys A 729, 129 (2003). PAIR ENERGY OF PROTON AND NEUTRON IN ATOMIC NUCLEI Nurmukhamedov A.M. Institute of Nuclear Physics, Tashkent, Uzbekistan The work [1] demonstrated that the structure of Wigner’s mass formula contains pairing of nucleons. Taking into account that the pair energy is playing significant role in nuclear events and in a view of new data we would like to review this issue again. -

Charge Radius of the Short-Lived Ni68 and Correlation with The
PHYSICAL REVIEW LETTERS 124, 132502 (2020) Charge Radius of the Short-Lived 68Ni and Correlation with the Dipole Polarizability † S. Kaufmann,1 J. Simonis,2 S. Bacca,2,3 J. Billowes,4 M. L. Bissell,4 K. Blaum ,5 B. Cheal,6 R. F. Garcia Ruiz,4,7, W. Gins,8 C. Gorges,1 G. Hagen,9 H. Heylen,5,7 A. Kanellakopoulos ,8 S. Malbrunot-Ettenauer,7 M. Miorelli,10 R. Neugart,5,11 ‡ G. Neyens ,7,8 W. Nörtershäuser ,1,* R. Sánchez ,12 S. Sailer,13 A. Schwenk,1,5,14 T. Ratajczyk,1 L. V. Rodríguez,15, L. Wehner,16 C. Wraith,6 L. Xie,4 Z. Y. Xu,8 X. F. Yang,8,17 and D. T. Yordanov15 1Institut für Kernphysik, Technische Universität Darmstadt, D-64289 Darmstadt, Germany 2Institut für Kernphysik and PRISMA+ Cluster of Excellence, Johannes Gutenberg-Universität Mainz, D-55128 Mainz, Germany 3Helmholtz Institute Mainz, GSI Helmholtzzentrum für Schwerionenforschung GmbH, D-64291 Darmstadt, Germany 4School of Physics and Astronomy, The University of Manchester, Manchester, M13 9PL, United Kingdom 5Max-Planck-Institut für Kernphysik, D-69117 Heidelberg, Germany 6Oliver Lodge Laboratory, Oxford Street, University of Liverpool, Liverpool L69 7ZE, United Kingdom 7Experimental Physics Department, CERN, CH-1211 Geneva 23, Switzerland 8KU Leuven, Instituut voor Kern- en Stralingsfysica, B-3001 Leuven, Belgium 9Physics Division, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA and Department of Physics and Astronomy, University of Tennessee, Knoxville, Tennessee 37996, USA 10TRIUMF, 4004 Wesbrook Mall, Vancouver, British Columbia, V6T 2A3, Canada 11Institut -

Muonic Atoms and Radii of the Lightest Nuclei
Muonic atoms and radii of the lightest nuclei Randolf Pohl Uni Mainz MPQ Garching Tihany 10 June 2019 Outline ● Muonic hydrogen, deuterium and the Proton Radius Puzzle New results from H spectroscopy, e-p scattering ● Muonic helium-3 and -4 Charge radii and the isotope shift ● Muonic present: HFS in μH, μ3He 10x better (magnetic) Zemach radii ● Muonic future: muonic Li, Be 10-100x better charge radii ● Ongoing: Triton charge radius from atomic T(1S-2S) 400fold improved triton charge radius Nuclear rms charge radii from measurements with electrons values in fm * elastic electron scattering * H/D: laser spectroscopy and QED (a lot!) * He, Li, …. isotope shift for charge radius differences * for medium-high Z (C and above): muonic x-ray spectroscopy sources: * p,d: CODATA-2014 * t: Amroun et al. (Saclay) , NPA 579, 596 (1994) * 3,4He: Sick, J.Phys.Chem.Ref Data 44, 031213 (2015) * Angeli, At. Data Nucl. Data Tab. 99, 69 (2013) The “Proton Radius Puzzle” Measuring Rp using electrons: 0.88 fm ( +- 0.7%) using muons: 0.84 fm ( +- 0.05%) 0.84 fm 0.88 fm 5 μd 2016 CODATA-2014 4 μp 2013 5.6 σ 3 e-p scatt. μp 2010 2 H spectroscopy 1 0.83 0.84 0.85 0.86 0.87 0.88 0.89 0.9 Proton charge radius R [fm] ch μd 2016: RP et al (CREMA Coll.) Science 353, 669 (2016) μp 2013: A. Antognini, RP et al (CREMA Coll.) Science 339, 417 (2013) The “Proton Radius Puzzle” Measuring Rp using electrons: 0.88 fm ( +- 0.7%) using muons: 0.84 fm ( +- 0.05%) 0.84 fm 0.88 fm 5 μd 2016 CODATA-2014 4 μp 2013 5.6 σ 3 e-p scatt. -

The MITP Proton Radius Puzzle Workshop
Report on The MITP Proton Radius Puzzle Workshop June 2–6, 2014 in Waldthausen Castle, Mainz, Germany 1 Description of the Workshop The organizers of the workshop were: • Carl Carlson, William & Mary, [email protected] • Richard Hill, University of Chicago, [email protected] • Savely Karshenboim, MPI fur¨ Quantenoptik & Pulkovo Observatory, [email protected] • Marc Vanderhaeghen, Universitat¨ Mainz, [email protected] The web page of the workshop, which contains all talks, can be found at https://indico.mitp.uni-mainz.de/conferenceDisplay.py?confId=14 . The size of the proton is one of the most fundamental observables in hadron physics. It is measured through an electromagnetic form factor. The latter is directly related to the distribution of charge and magnetization of the baryon and through such imaging provides the basis of nearly all studies of the hadron structure. In very recent years, a very precise knowledge of nucleon form factors has become more and more im- portant as input for precision experiments in several fields of physics. Well known examples are the hydrogen Lamb shift and the hydrogen hyperfine splitting. The atomic physics measurements of energy level splittings reach an impressive accuracy of up to 13 significant digits. Its theoretical understanding however is far less accurate, being at the part-per-million level (ppm). The main theoretical uncertainty lies in proton structure corrections, which limits the search for new physics in these kinds of experiment. In this context, the recent PSI measurement of the proton charge radius from the Lamb shift in muonic hydrogen has given a value that is a startling 4%, or 5 standard deviations, lower than the values ob- tained from energy level shifts in electronic hydrogen and from electron-proton scattering experiments, see figure below. -

Prospects for Measurements with Strange Hadrons at Lhcb
Prospects for measurements with strange hadrons at LHCb A. A. Alves Junior1, M. O. Bettler2, A. Brea Rodr´ıguez1, A. Casais Vidal1, V. Chobanova1, X. Cid Vidal1, A. Contu3, G. D'Ambrosio4, J. Dalseno1, F. Dettori5, V.V. Gligorov6, G. Graziani7, D. Guadagnoli8, T. Kitahara9;10, C. Lazzeroni11, M. Lucio Mart´ınez1, M. Moulson12, C. Mar´ınBenito13, J. Mart´ınCamalich14;15, D. Mart´ınezSantos1, J. Prisciandaro 1, A. Puig Navarro16, M. Ramos Pernas1, V. Renaudin13, A. Sergi11, K. A. Zarebski11 1Instituto Galego de F´ısica de Altas Enerx´ıas(IGFAE), Santiago de Compostela, Spain 2Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom 3INFN Sezione di Cagliari, Cagliari, Italy 4INFN Sezione di Napoli, Napoli, Italy 5Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom, now at Universit`adegli Studi di Cagliari, Cagliari, Italy 6LPNHE, Sorbonne Universit´e,Universit´eParis Diderot, CNRS/IN2P3, Paris, France 7INFN Sezione di Firenze, Firenze, Italy 8Laboratoire d'Annecy-le-Vieux de Physique Th´eorique , Annecy Cedex, France 9Institute for Theoretical Particle Physics (TTP), Karlsruhe Institute of Technology, Kalsruhe, Germany 10Institute for Nuclear Physics (IKP), Karlsruhe Institute of Technology, Kalsruhe, Germany 11School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom 12INFN Laboratori Nazionali di Frascati, Frascati, Italy 13Laboratoire de l'Accelerateur Lineaire (LAL), Orsay, France 14Instituto de Astrof´ısica de Canarias and Universidad de La Laguna, Departamento de Astrof´ısica, La Laguna, Tenerife, Spain 15CERN, CH-1211, Geneva 23, Switzerland 16Physik-Institut, Universit¨atZ¨urich,Z¨urich,Switzerland arXiv:1808.03477v2 [hep-ex] 31 Jul 2019 Abstract This report details the capabilities of LHCb and its upgrades towards the study of kaons and hyperons. -

Physics Has a Core Problem
Physics Has a Core Problem Physicists can solve many puzzles by taking more accurate and careful measurements. Randolf Pohl and his colleagues at the Max Planck Institute of Quantum Optics in Garching, however, actually created a new problem with their precise measurements of the proton radius, because the value they measured differs significantly from the value previously considered to be valid. The difference could point to gaps in physicists’ picture of matter. Measuring with a light ruler: Randolf Pohl and his team used laser spectroscopy to determine the proton radius – and got a surprising result. PHYSICS & ASTRONOMY_Proton Radius TEXT PETER HERGERSBERG he atmosphere at the scien- tific conferences that Ran- dolf Pohl has attended in the past three years has been very lively. And the T physicist from the Max Planck Institute of Quantum Optics is a good part of the reason for this liveliness: the commu- nity of experts that gathers there is working together to solve a puzzle that Pohl and his team created with its mea- surements of the proton radius. Time and time again, speakers present possible solutions and substantiate them with mathematically formulated arguments. In the process, they some- times also cast doubt on theories that for decades have been considered veri- fied. Other speakers try to find weak spots in their fellow scientists’ explana- tions, and present their own calcula- tions to refute others’ hypotheses. In the end, everyone goes back to their desks and their labs to come up with subtle new deliberations to fuel the de- bate at the next meeting. In 2010, the Garching-based physi- cists, in collaboration with an interna- tional team, published a new value for the charge radius of the proton – that is, the nucleus at the core of a hydro- gen atom. -

Dark Matter in Nuclear Physics
Dark Matter in Nuclear Physics George Fuller (UCSD), Andrew Hime (LANL), Reyco Henning (UNC), Darin Kinion (LLNL), Spencer Klein (LBNL), Stefano Profumo (Caltech) Michael Ramsey-Musolf (Caltech/UW Madison), Robert Stokstad (LBNL) Introduction A transcendent accomplishment of nuclear physics and observational cosmology has been the definitive measurement of the baryon content of the universe. Big Bang Nucleosynthesis calculations, combined with measurements made with the largest new telescopes of the primordial deuterium abundance, have inferred the baryon density of the universe. This result has been confirmed by observations of the anisotropies in the Cosmic Microwave Background. The surprising upshot is that baryons account for only a small fraction of the observed mass and energy in the universe. It is now firmly established that most of the mass-energy in the Universe is comprised of non-luminous and unknown forms. One component of this is the so- called “dark energy”, believed to be responsible for the observed acceleration of the expansion rate of the universe. Another component appears to be composed of non-luminous material with non-relativistic kinematics at the current epoch. The relationship between the dark matter and the dark energy is unknown. Several national studies and task-force reports have found that the identification of the mysterious “dark matter” is one of the most important pursuits in modern science. It is now clear that an explanation for this phenomenon will require some sort of new physics, likely involving a new particle or particles, and in any case involving physics beyond the Standard Model. A large number of dark matter studies, from theory to direct dark matter particle detection, involve nuclear physics and nuclear physicists. -

Electron Charge Density: a Clue from Quantum Chemistry for Quantum Foundations
Electron Charge Density: A Clue from Quantum Chemistry for Quantum Foundations Charles T. Sebens California Institute of Technology arXiv v.2 June 24, 2021 Forthcoming in Foundations of Physics Abstract Within quantum chemistry, the electron clouds that surround nuclei in atoms and molecules are sometimes treated as clouds of probability and sometimes as clouds of charge. These two roles, tracing back to Schr¨odingerand Born, are in tension with one another but are not incompatible. Schr¨odinger'sidea that the nucleus of an atom is surrounded by a spread-out electron charge density is supported by a variety of evidence from quantum chemistry, including two methods that are used to determine atomic and molecular structure: the Hartree-Fock method and density functional theory. Taking this evidence as a clue to the foundations of quantum physics, Schr¨odinger'selectron charge density can be incorporated into many different interpretations of quantum mechanics (and extensions of such interpretations to quantum field theory). Contents 1 Introduction2 2 Probability Density and Charge Density3 3 Charge Density in Quantum Chemistry9 3.1 The Hartree-Fock Method . 10 arXiv:2105.11988v2 [quant-ph] 24 Jun 2021 3.2 Density Functional Theory . 20 3.3 Further Evidence . 25 4 Charge Density in Quantum Foundations 26 4.1 GRW Theory . 26 4.2 The Many-Worlds Interpretation . 29 4.3 Bohmian Mechanics and Other Particle Interpretations . 31 4.4 Quantum Field Theory . 33 5 Conclusion 35 1 1 Introduction Despite the massive progress that has been made in physics, the composition of the atom remains unsettled. J. J. Thomson [1] famously advocated a \plum pudding" model where electrons are seen as tiny negative charges inside a sphere of uniformly distributed positive charge (like the raisins|once called \plums"|suspended in a plum pudding). -

Lepton Probes in Nuclear Physics
L C f' - l ■) aboratoire ATIONAI FR9601644 ATURNE 91191 Gif-sur-Yvette Cedex France LEPTON PROBES IN NUCLEAR PHYSICS J. ARVIEUX Laboratoire National Saturne IN2P3-CNRS A DSM-CEA, CESaclay F-9I191 Gif-sur-Yvette Cedex, France EPS Conference : Large Facilities in Physics, Lausanne (Switzerland) Sept. 12-14, 1994 ££)\-LNS/Ph/94-18 Centre National de la Recherche Scientifique CBD Commissariat a I’Energie Atomique VOL LEPTON PROBES IN NUCLEAR PHYSICS J. ARVTEUX Laboratoire National Saturne IN2P3-CNRS &. DSM-CEA, CESaclay F-91191 Gif-sur-Yvette Cedex, France ABSTRACT 1. Introduction This review concerns the facilities which use the lepton probe to learn about nuclear physics. Since this Conference is attended by a large audience coming from diverse horizons, a few definitions may help to explain what I am going to talk about. 1.1. Leptons versus hadrons The particle physics world is divided in leptons and hadrons. Leptons are truly fundamental particles which are point-like (their dimension cannot be measured) and which interact with matter through two well-known forces : the electromagnetic interaction and the weak interaction which have been regrouped in the 70's in the single electroweak interaction following the theoretical insight of S. Weinberg (Nobel prize in 1979) and the experimental discoveries of the Z° and W±- bosons at CERN by C. Rubbia and Collaborators (Nobel prize in 1984). The leptons comprise 3 families : electrons (e), muons (jt) and tau (r) and their corresponding neutrinos : ve, and vr . Nuclear physics can make use of electrons and muons but since muons are produced at large energy accelerators, they more or less belong to the particle world although they can also be used to study solid state physics. -

The Nuclear Physics of Neutron Stars
The Nuclear Physics of Neutron Stars Exotic Beam Summer School 2015 Florida State University Tallahassee, FL - August 2015 J. Piekarewicz (FSU) Neutron Stars EBSS 2015 1 / 21 My FSU Collaborators My Outside Collaborators Genaro Toledo-Sanchez B. Agrawal (Saha Inst.) Karim Hasnaoui M. Centelles (U. Barcelona) Bonnie Todd-Rutel G. Colò (U. Milano) Brad Futch C.J. Horowitz (Indiana U.) Jutri Taruna W. Nazarewicz (MSU) Farrukh Fattoyev N. Paar (U. Zagreb) Wei-Chia Chen M.A. Pérez-Garcia (U. Raditya Utama Salamanca) P.G.- Reinhard (U. Erlangen-Nürnberg) X. Roca-Maza (U. Milano) D. Vretenar (U. Zagreb) J. Piekarewicz (FSU) Neutron Stars EBSS 2015 2 / 21 S. Chandrasekhar and X-Ray Chandra White dwarfs resist gravitational collapse through electron degeneracy pressure rather than thermal pressure (Dirac and R.H. Fowler 1926) During his travel to graduate school at Cambridge under Fowler, Chandra works out the physics of the relativistic degenerate electron gas in white dwarf stars (at the age of 19!) For masses in excess of M =1:4 M electrons becomes relativistic and the degeneracy pressure is insufficient to balance the star’s gravitational attraction (P n5=3 n4=3) ∼ ! “For a star of small mass the white-dwarf stage is an initial step towards complete extinction. A star of large mass cannot pass into the white-dwarf stage and one is left speculating on other possibilities” (S. Chandrasekhar 1931) Arthur Eddington (1919 bending of light) publicly ridiculed Chandra’s on his discovery Awarded the Nobel Prize in Physics (in 1983 with W.A. Fowler) In 1999, NASA lunches “Chandra” the premier USA X-ray observatory J. -

Introduction to Nuclear Physics and Nuclear Decay
NM Basic Sci.Intro.Nucl.Phys. 06/09/2011 Introduction to Nuclear Physics and Nuclear Decay Larry MacDonald [email protected] Nuclear Medicine Basic Science Lectures September 6, 2011 Atoms Nucleus: ~10-14 m diameter ~1017 kg/m3 Electron clouds: ~10-10 m diameter (= size of atom) water molecule: ~10-10 m diameter ~103 kg/m3 Nucleons (protons and neutrons) are ~10,000 times smaller than the atom, and ~1800 times more massive than electrons. (electron size < 10-22 m (only an upper limit can be estimated)) Nuclear and atomic units of length 10-15 = femtometer (fm) 10-10 = angstrom (Å) Molecules mostly empty space ~ one trillionth of volume occupied by mass Water Hecht, Physics, 1994 (wikipedia) [email protected] 2 [email protected] 1 NM Basic Sci.Intro.Nucl.Phys. 06/09/2011 Mass and Energy Units and Mass-Energy Equivalence Mass atomic mass unit, u (or amu): mass of 12C ≡ 12.0000 u = 19.9265 x 10-27 kg Energy Electron volt, eV ≡ kinetic energy attained by an electron accelerated through 1.0 volt 1 eV ≡ (1.6 x10-19 Coulomb)*(1.0 volt) = 1.6 x10-19 J 2 E = mc c = 3 x 108 m/s speed of light -27 2 mass of proton, mp = 1.6724x10 kg = 1.007276 u = 938.3 MeV/c -27 2 mass of neutron, mn = 1.6747x10 kg = 1.008655 u = 939.6 MeV/c -31 2 mass of electron, me = 9.108x10 kg = 0.000548 u = 0.511 MeV/c [email protected] 3 Elements Named for their number of protons X = element symbol Z (atomic number) = number of protons in nucleus N = number of neutrons in nucleus A A A A (atomic mass number) = Z + N Z X N Z X X [A is different than, but approximately equal to the atomic weight of an atom in amu] Examples; oxygen, lead A Electrically neural atom, Z X N has Z electrons in its 16 208 atomic orbit.