DOCSLIB.ORG

The Nuclear Physics of Neutron Stars

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Nuclear Physics of Neutron Stars The Nuclear Physics of Neutron Stars Exotic Beam Summer School 2015 Florida State University Tallahassee, FL - August 2015 J. Piekarewicz (FSU) Neutron Stars EBSS 2015 1 / 21 My FSU Collaborators My Outside Collaborators Genaro Toledo-Sanchez B. Agrawal (Saha Inst.) Karim Hasnaoui M. Centelles (U. Barcelona) Bonnie Todd-Rutel G. Colò (U. Milano) Brad Futch C.J. Horowitz (Indiana U.) Jutri Taruna W. Nazarewicz (MSU) Farrukh Fattoyev N. Paar (U. Zagreb) Wei-Chia Chen M.A. Pérez-Garcia (U. Raditya Utama Salamanca) P.G.- Reinhard (U. Erlangen-Nürnberg) X. Roca-Maza (U. Milano) D. Vretenar (U. Zagreb) J. Piekarewicz (FSU) Neutron Stars EBSS 2015 2 / 21 S. Chandrasekhar and X-Ray Chandra White dwarfs resist gravitational collapse through electron degeneracy pressure rather than thermal pressure (Dirac and R.H. Fowler 1926) During his travel to graduate school at Cambridge under Fowler, Chandra works out the physics of the relativistic degenerate electron gas in white dwarf stars (at the age of 19!) For masses in excess of M =1:4 M electrons becomes relativistic and the degeneracy pressure is insufficient to balance the star’s gravitational attraction (P n5=3 n4=3) ∼ ! “For a star of small mass the white-dwarf stage is an initial step towards complete extinction. A star of large mass cannot pass into the white-dwarf stage and one is left speculating on other possibilities” (S. Chandrasekhar 1931) Arthur Eddington (1919 bending of light) publicly ridiculed Chandra’s on his discovery Awarded the Nobel Prize in Physics (in 1983 with W.A. Fowler) In 1999, NASA lunches “Chandra” the premier USA X-ray observatory J. Piekarewicz (FSU) Neutron Stars EBSS 2015 3 / 21 Some Historical Facts Chandrasekhar shows that massive stars will collapse (1931) Chadwick discovers the neutron (1932) ... predicted earlier by Ettore Majorana but never published! Baade and Zwicky introduce the concept of neutron stars (1933) Oppenheimer-Volkoff compute masses of neutron stars using GR (1939) Predict M? '0:7 M as maximum NS mass or minimum black hole mass Jocelyn Bell discovers pulsars (1967) Gold and Pacini propose basic lighthouse model (1968) Pulsars are rapidly rotating Neutron Stars! J. Piekarewicz (FSU) Neutron Stars EBSS 2015 4 / 21 Jocelyn Bell Worked with Anthony Hewish on constructing a radio telescope to study quasars In 1967 as a graduate student (at the age of 24!) detected a bit of “scruff” Jocelyn Bell discovers amazing regularity in the radio signals( P =1:33730119 s) Speculated that the signal might be from another civilization (LGM-1) Paper announcing the first pulsar published in Nature (February 1968) A Hewish, S J Bell, J D H Pilkington, P F Scott, R A Collins Antony Hewish and Martin Ryle awarded the Nobel Prize in Physics in 1974 The “No-Bell” roundly condemned by many astronomers (Fred Hoyle) “I believe it would demean Nobel Prizes if they were awarded to research students, except in very exceptional cases, and I do not believe this is one of them” J. Piekarewicz (FSU) Neutron Stars EBSS 2015 5 / 21 Table of Contents 5 Neutron Star Crust: Preface by Jocelyn Bell Table of Contents Preface ...................................................................... 1 Introduction ................................................................. 3 Neutron star crust and molecular dynamics simulation C. J. Horowitz, J. Hughto, A. Schneider, and D. K. Berry . 6 Nuclear pasta in supernovae and neutron stars Preface 1 G. Watanabe and2JocelynBellBurnell T. Maruyama . 26 Terrestrial andthe field, astrophysical both observational andsuperfluidity: theoretical, and identify coldsome atoms of the critical and problems neutron on matter A. Gezerlis andwhich J. majorCarlson progress may . .be . expected. .in . the . next . .. decade. 48 Dr. Carlos Bertulani’s and Dr. Jorge Piekarewicz’s goal has been to put together a Pairing correlationscomprehensive and review thermodynamic of some of the main theoretical properties ideas related of toinner the structure crust and matter dynamics of neutron stars, with special emphasis on the nuclear physics. I have found J. Margueron andthe idea N. very Sandulescu timely and have gladly . accepted . their . invitati . .on . to . write. .. the . preface . to. this . 68 Preface The crust ofcollection spinning-down of review articles. neutron stars Ibelievethatthisbookwillhaveawidereadership.Mostarticles are accessible to a R. Negreiros, S.graduate Schramm, student, or to and a non-practitioner F. Weber researcher, . wit . .hout . much. knowledge . of. the . field. 87 Moreover, I expect that this book will become a useful resource for the many established Influence ofpractitioners. the nuclear I hope you symmetry agree with me, find energy the book enjoyabon thele tostructure read, and useful to and have composition of the Jocelyn Bell Burnell ∗ University of Oxford, Denys Wilkinson Building outer crust on your shelves. Keble Road, Oxford OX1 3RH, UK X. Roca-Maza, J. Piekarewicz, T. Garc´ıa-Galvez,´ and M. Centelles . 104 Jocelyn Bell Burnell Equation of stateUniversity for of Oxford proto-neutron star Ijudgemyselffortunatetobeworkinginanexcitingandfastmoving area January 2012 of science and at a time when the public has become fascinated by questions re- G.Shen .................................................................... 129 garding the birth and evolution of stars, the nature of dark matter and dark en- From nuclei to nuclear pasta ergy, the formation of black holes and the origin and evolution of the universe. C.O. Dorso, P.A. G´ımenez-Molinelli, and J.A. Lopez´ . 151 The physics of neutron stars is one of these fas- The structure of the neutron star crust within a semi-microscopic energy density func- cinating subjects. Neutron stars are formed in su- pernova explosions of massive stars or by accretion- tional method induced collapse of smaller white dwarf stars. Their existence was confirmed through the discovery of ra- M. Baldo and E.E. Saperstein . 171 dio pulsars during my thesis work in 1967. Since The inner crust and its structure then this field has evolved enormously. Today we know of accretion-powered pulsars which are pre- D.P. Menezes, S.S. Avancini, C. Providencia,ˆ and M.D. Alloy . 194 dominantly bright X-ray sources, rotation-powered pulsars observed throughout the electromagnetic Neutron-star crusts and finite nuclei spectrum, radio-quiet neutron stars, and highly mag- S. Goriely, J. M. Pearson, and N. Chamel . 214 netized neutron stars or magnetars. No wonder there has been an explosion in the research activity related The nuclear symmetry energy, the inner crust, and global neutron star modeling to neutron stars! W.G. Newton, M. Gearheart, J. Hooker, and Bao-An Li . 236 It is now hard to collect in a single book what we already know about neutron stars along with some of Neutron starquakes and the dynamic crust the exciting new developments. In this volume ex- perts have been asked to articulate what they believe A.L.Watts . 266 are the critical, open questions in the field. In order for the book to be useful to a more Thermal and transport properties of the neutron star inner crust general audience, the presentations also aim to be as pedagogical as possible. This book is a collection of articles on the neutron stars themselves, written by well- D. Page and S. Reddy . 282 known physicists. It is written with young researchers as thetargetaudience,tohelpthis new generation move the field forward. The invited authors summarize the current status of Quantum description of the low-density inner crust: finite size effects and linear re- ∗[email protected] sponse, superfluidity, vortices P. Avogadro, F. Barranco, R.A. Broglia, and E. Vigezzi . 309 J. Piekarewicz (FSU) Neutron Stars EBSS 2015 6 / 21 Biography of a Neutron Star: The Crab Pulsar SN 1054 first observed as a new “star” in the sky on July 4, 1054 Event recorded in multiple Chinese and Japanese documents Event also recorded by Anasazi residents of Chaco Canyon, NM Crab nebula and pulsar became the SN remnants Name: PSR B0531+21 Distance: 6,500 ly POB: Taurus Temperature: 106 K Mass: 1.4 M Density: 1014g/cm3 Radius: 10 km Pressure: 1029 atm Period: 33 ms Magnetic Field: 1012 G J. Piekarewicz (FSU) Neutron Stars EBSS 2015 7 / 21 A Grand Challenge: How does subatomic matter organize itself? “Nuclear Physics: Exploring the Heart of Matter” (2010 Committee on the Assessment and Outlook for Nuclear Physics) Consider A nucleons and Z leptons in a fixed volume V at T ≡0 ... cold fully catalyzed matter in thermal and chemical equilibrium Enforce charge neutrality protons = electrons + muons Enforce chemical (i.e., beta) equilibrium: n!p+e− +¯ν; p+e− !n+ν Impossible to answer such a question under normal laboratory conditions — as such a system is in general unbound! J. Piekarewicz (FSU) Neutron Stars EBSS 2015 8 / 21 Neutron Stars as Nuclear Physics Gold Mines Neutron Stars are the remnants of massive stellar explosions Are bound by gravity NOT by the strong force Satisfy the Tolman-Oppenheimer-Volkoff equation( vesc=c ∼1=2) Only Physics sensitive to: Equation of state of neutron-rich matter EOS must span about 11 orders of magnitude in baryon density Increase from 0.7!2M must be explained byLETTER NuclearRESEARCH Physics! Received 7 July;dM accepted 1 September 2010. MS0 2 2.5 GR MPA1 = 4 r E(r) ∞ AP3 1. Lattimer, J. M. & Prakash, M. Theπ physics of neutron stars. Science 304, 536–542 < PAL1 P ENG (2004). dr AP4 MS2 2. Lattimer, J. M. & Prakash, M. Neutron star observations: prognosis for equation of Causality state constraints.dP Phys. Rep. 442, 109–165E(r (2007).)M(r) P(r) 2.0 J1614-2230 3. Glendenning, N. K. &= Schaffner-Bielich,−G J. Kaon condensation and1 dynamical+ SQM3 MS1 nucleons in neutron stars. Phys. Rev. Lett. 81, 4564–45672 (1998). J1903+0327 FSU 4. Lackey, B. D.,dr Nayyar, M. & Owen, B. J. Observationalr constraints on hyperonsE in (r) ) ( SQM1 PAL6 GM3 neutron stars.
Load more

Recommended publications
  • Neutron Stars
    Chandra X-Ray Observatory X-Ray Astronomy Field Guide Neutron Stars Ordinary matter, or the stuff we and everything around us is made of, consists largely of empty space. Even a rock is mostly empty space. This is because matter is made of atoms. An atom is a cloud of electrons orbiting around a nucleus composed of protons and neutrons. The nucleus contains more than 99.9 percent of the mass of an atom, yet it has a diameter of only 1/100,000 that of the electron cloud. The electrons themselves take up little space, but the pattern of their orbit defines the size of the atom, which is therefore 99.9999999999999% Chandra Image of Vela Pulsar open space! (NASA/PSU/G.Pavlov et al. What we perceive as painfully solid when we bump against a rock is really a hurly-burly of electrons moving through empty space so fast that we can't see—or feel—the emptiness. What would matter look like if it weren't empty, if we could crush the electron cloud down to the size of the nucleus? Suppose we could generate a force strong enough to crush all the emptiness out of a rock roughly the size of a football stadium. The rock would be squeezed down to the size of a grain of sand and would still weigh 4 million tons! Such extreme forces occur in nature when the central part of a massive star collapses to form a neutron star. The atoms are crushed completely, and the electrons are jammed inside the protons to form a star composed almost entirely of neutrons.
    [Show full text]
  • The Five Common Particles
    The Five Common Particles The world around you consists of only three particles: protons, neutrons, and electrons. Protons and neutrons form the nuclei of atoms, and electrons glue everything together and create chemicals and materials. Along with the photon and the neutrino, these particles are essentially the only ones that exist in our solar system, because all the other subatomic particles have half-lives of typically 10-9 second or less, and vanish almost the instant they are created by nuclear reactions in the Sun, etc. Particles interact via the four fundamental forces of nature. Some basic properties of these forces are summarized below. (Other aspects of the fundamental forces are also discussed in the Summary of Particle Physics document on this web site.) Force Range Common Particles It Affects Conserved Quantity gravity infinite neutron, proton, electron, neutrino, photon mass-energy electromagnetic infinite proton, electron, photon charge -14 strong nuclear force ≈ 10 m neutron, proton baryon number -15 weak nuclear force ≈ 10 m neutron, proton, electron, neutrino lepton number Every particle in nature has specific values of all four of the conserved quantities associated with each force. The values for the five common particles are: Particle Rest Mass1 Charge2 Baryon # Lepton # proton 938.3 MeV/c2 +1 e +1 0 neutron 939.6 MeV/c2 0 +1 0 electron 0.511 MeV/c2 -1 e 0 +1 neutrino ≈ 1 eV/c2 0 0 +1 photon 0 eV/c2 0 0 0 1) MeV = mega-electron-volt = 106 eV. It is customary in particle physics to measure the mass of a particle in terms of how much energy it would represent if it were converted via E = mc2.
    [Show full text]
  • Photons from 252Cf and 241Am-Be Neutron Sources H
    Neutronenbestrahlungsraum Calibration Laboratory LB6411 Am-Be Quelle [email protected] Photons from 252Cf and 241Am-Be neutron sources H. Hoedlmoser, M. Boschung, K. Meier and S. Mayer Paul Scherrer Institut, CH-5232 Villigen PSI, Switzerland At the accredited PSI calibration laboratory neutron reference fields traceable to the standards of the Physikalisch-Technische Bundesanstalt (PTB) in Germany are available for the calibration of ambient and personal dose equivalent (rate) meters and passive dosimeters. The photon contribution to H*(10) in the neutron fields of the 252Cf and 241Am-Be sources was measured using various photon dose rate meters and active and passive dosimeters. Measuring photons from a neutron source involves considerable uncertainties due to the presence of neutrons, due to a non-zero neutron sensitivity of the photon detector and due to the energy response of the photon detectors. Therefore eight independent detectors and methods were used to obtain a reliable estimate for the photon contribution as an average of the individual methods. For the 241Am-Be source a photon contribution of approximately 4.9% was determined and for the 252Cf source a contribution of 3.6%. 1) Photon detectors 2) Photons from 252Cf and 241Am-Be neutron sources Figure 1 252Cf decays through -emission (~97%) and through spontaneous fission (~3%) with a half-life of 2.65 y. Both processes are accompanied by photon radiation. Furthermore the spectrum of fission products contains radioactive elements that produce additional gamma photons. In the 241Am-Be source 241Am decays through -emission and various low energy emissions: 241Am237Np + + with a half life of 432.6 y.
    [Show full text]
  • B2.IV Nuclear and Particle Physics
    B2.IV Nuclear and Particle Physics A.J. Barr February 13, 2014 ii Contents 1 Introduction 1 2 Nuclear 3 2.1 Structure of matter and energy scales . 3 2.2 Binding Energy . 4 2.2.1 Semi-empirical mass formula . 4 2.3 Decays and reactions . 8 2.3.1 Alpha Decays . 10 2.3.2 Beta decays . 13 2.4 Nuclear Scattering . 18 2.4.1 Cross sections . 18 2.4.2 Resonances and the Breit-Wigner formula . 19 2.4.3 Nuclear scattering and form factors . 22 2.5 Key points . 24 Appendices 25 2.A Natural units . 25 2.B Tools . 26 2.B.1 Decays and the Fermi Golden Rule . 26 2.B.2 Density of states . 26 2.B.3 Fermi G.R. example . 27 2.B.4 Lifetimes and decays . 27 2.B.5 The flux factor . 28 2.B.6 Luminosity . 28 2.C Shell Model § ............................. 29 2.D Gamma decays § ............................ 29 3 Hadrons 33 3.1 Introduction . 33 3.1.1 Pions . 33 3.1.2 Baryon number conservation . 34 3.1.3 Delta baryons . 35 3.2 Linear Accelerators . 36 iii CONTENTS CONTENTS 3.3 Symmetries . 36 3.3.1 Baryons . 37 3.3.2 Mesons . 37 3.3.3 Quark flow diagrams . 38 3.3.4 Strangeness . 39 3.3.5 Pseudoscalar octet . 40 3.3.6 Baryon octet . 40 3.4 Colour . 41 3.5 Heavier quarks . 43 3.6 Charmonium . 45 3.7 Hadron decays . 47 Appendices 48 3.A Isospin § ................................ 49 3.B Discovery of the Omega § ......................
    [Show full text]
  • Astromaterial Science and Nuclear Pasta
    Astromaterial Science and Nuclear Pasta M. E. Caplan∗ and C. J. Horowitzy Center for Exploration of Energy and Matter and Department of Physics, Indiana University, Bloomington, IN 47405, USA (Dated: June 28, 2017) We define `astromaterial science' as the study of materials in astronomical objects that are qualitatively denser than materials on earth. Astromaterials can have unique prop- erties related to their large density, though they may be organized in ways similar to more conventional materials. By analogy to terrestrial materials, we divide our study of astromaterials into hard and soft and discuss one example of each. The hard as- tromaterial discussed here is a crystalline lattice, such as the Coulomb crystals in the interior of cold white dwarfs and in the crust of neutron stars, while the soft astro- material is nuclear pasta found in the inner crusts of neutron stars. In particular, we discuss how molecular dynamics simulations have been used to calculate the properties of astromaterials to interpret observations of white dwarfs and neutron stars. Coulomb crystals are studied to understand how compact stars freeze. Their incredible strength may make crust \mountains" on rotating neutron stars a source for gravitational waves that the Laser Interferometer Gravitational-Wave Observatory (LIGO) may detect. Nu- clear pasta is expected near the base of the neutron star crust at densities of 1014 g/cm3. Competition between nuclear attraction and Coulomb repulsion rearranges neutrons and protons into complex non-spherical shapes such as sheets (lasagna) or tubes (spaghetti). Semi-classical molecular dynamics simulations of nuclear pasta have been used to study these phases and calculate their transport properties such as neutrino opacity, thermal conductivity, and electrical conductivity.
    [Show full text]
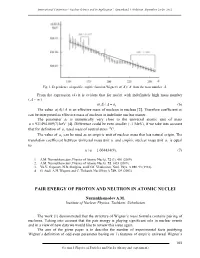
  • Pair Energy of Proton and Neutron in Atomic Nuclei
    International Conference “Nuclear Science and its Application”, Samarkand, Uzbekistan, September 25-28, 2012 Fig. 1. Dependence of specific empiric function Wigner's a()/ A A from the mass number A. From the expression (4) it is evident that for nuclei with indefinitely high mass number ( A ~ ) a()/. A A a1 (6) The value a()/ A A is an effective mass of nucleon in nucleus [2]. Therefore coefficient a1 can be interpreted as effective mass of nucleon in indefinite nuclear matter. The parameter a1 is numerically very close to the universal atomic unit of mass u 931494.009(7) keV [4]. Difference could be even smaller (~1 MeV), if we take into account that for definition of u, used mass of neutral atom 12C. The value of a1 can be used as an empiric unit of nuclear mass that has natural origin. The translation coefficient between universal mass unit u and empiric nuclear mass unit a1 is equal to: u/ a1 1.004434(9). (7) 1. A.M. Nurmukhamedov, Physics of Atomic Nuclei, 72 (3), 401 (2009). 2. A.M. Nurmukhamedov, Physics of Atomic Nuclei, 72, 1435 (2009). 3. Yu.V. Gaponov, N.B. Shulgina, and D.M. Vladimirov, Nucl. Phys. A 391, 93 (1982). 4. G. Audi, A.H. Wapstra and C. Thibault, Nucl.Phys A 729, 129 (2003). PAIR ENERGY OF PROTON AND NEUTRON IN ATOMIC NUCLEI Nurmukhamedov A.M. Institute of Nuclear Physics, Tashkent, Uzbekistan The work [1] demonstrated that the structure of Wigner’s mass formula contains pairing of nucleons. Taking into account that the pair energy is playing significant role in nuclear events and in a view of new data we would like to review this issue again.
    [Show full text]
  • Opportunities for Neutrino Physics at the Spallation Neutron Source (SNS)
    Opportunities for Neutrino Physics at the Spallation Neutron Source (SNS) Paper submitted for the 2008 Carolina International Symposium on Neutrino Physics Yu Efremenko1,2 and W R Hix2,1 1University of Tennessee, Knoxville TN 37919, USA 2Oak Ridge National Laboratory, Oak Ridge TN 37981, USA E-mail: [email protected] Abstract. In this paper we discuss opportunities for a neutrino program at the Spallation Neutrons Source (SNS) being commissioning at ORNL. Possible investigations can include study of neutrino-nuclear cross sections in the energy rage important for supernova dynamics and neutrino nucleosynthesis, search for neutrino-nucleus coherent scattering, and various tests of the standard model of electro-weak interactions. 1. Introduction It seems that only yesterday we gathered together here at Columbia for the first Carolina Neutrino Symposium on Neutrino Physics. To my great astonishment I realized it was already eight years ago. However by looking back we can see that enormous progress has been achieved in the field of neutrino science since that first meeting. Eight years ago we did not know which region of mixing parameters (SMA. LMA, LOW, Vac) [1] would explain the solar neutrino deficit. We did not know whether this deficit is due to neutrino oscillations or some other even more exotic phenomena, like neutrinos decay [2], or due to the some other effects [3]. Hints of neutrino oscillation of atmospheric neutrinos had not been confirmed in accelerator experiments. Double beta decay collaborations were just starting to think about experiments with sensitive masses of hundreds of kilograms. Eight years ago, very few considered that neutrinos can be used as a tool to study the Earth interior [4] or for non- proliferation [5].
    [Show full text]
  • Phase Transitions and the Casimir Effect in Neutron Stars
    University of Tennessee, Knoxville TRACE: Tennessee Research and Creative Exchange Masters Theses Graduate School 12-2017 Phase Transitions and the Casimir Effect in Neutron Stars William Patrick Moffitt University of Tennessee, Knoxville, [email protected] Follow this and additional works at: https://trace.tennessee.edu/utk_gradthes Part of the Other Physics Commons Recommended Citation Moffitt, William Patrick, "Phase Transitions and the Casimir Effect in Neutron Stars. " Master's Thesis, University of Tennessee, 2017. https://trace.tennessee.edu/utk_gradthes/4956 This Thesis is brought to you for free and open access by the Graduate School at TRACE: Tennessee Research and Creative Exchange. It has been accepted for inclusion in Masters Theses by an authorized administrator of TRACE: Tennessee Research and Creative Exchange. For more information, please contact [email protected]. To the Graduate Council: I am submitting herewith a thesis written by William Patrick Moffitt entitled "Phaser T ansitions and the Casimir Effect in Neutron Stars." I have examined the final electronic copy of this thesis for form and content and recommend that it be accepted in partial fulfillment of the requirements for the degree of Master of Science, with a major in Physics. Andrew W. Steiner, Major Professor We have read this thesis and recommend its acceptance: Marianne Breinig, Steve Johnston Accepted for the Council: Dixie L. Thompson Vice Provost and Dean of the Graduate School (Original signatures are on file with official studentecor r ds.) Phase Transitions and the Casimir Effect in Neutron Stars A Thesis Presented for the Master of Science Degree The University of Tennessee, Knoxville William Patrick Moffitt December 2017 Abstract What lies at the core of a neutron star is still a highly debated topic, with both the composition and the physical interactions in question.
    [Show full text]
  • Prospects for Measurements with Strange Hadrons at Lhcb
    Prospects for measurements with strange hadrons at LHCb A. A. Alves Junior1, M. O. Bettler2, A. Brea Rodr´ıguez1, A. Casais Vidal1, V. Chobanova1, X. Cid Vidal1, A. Contu3, G. D'Ambrosio4, J. Dalseno1, F. Dettori5, V.V. Gligorov6, G. Graziani7, D. Guadagnoli8, T. Kitahara9;10, C. Lazzeroni11, M. Lucio Mart´ınez1, M. Moulson12, C. Mar´ınBenito13, J. Mart´ınCamalich14;15, D. Mart´ınezSantos1, J. Prisciandaro 1, A. Puig Navarro16, M. Ramos Pernas1, V. Renaudin13, A. Sergi11, K. A. Zarebski11 1Instituto Galego de F´ısica de Altas Enerx´ıas(IGFAE), Santiago de Compostela, Spain 2Cavendish Laboratory, University of Cambridge, Cambridge, United Kingdom 3INFN Sezione di Cagliari, Cagliari, Italy 4INFN Sezione di Napoli, Napoli, Italy 5Oliver Lodge Laboratory, University of Liverpool, Liverpool, United Kingdom, now at Universit`adegli Studi di Cagliari, Cagliari, Italy 6LPNHE, Sorbonne Universit´e,Universit´eParis Diderot, CNRS/IN2P3, Paris, France 7INFN Sezione di Firenze, Firenze, Italy 8Laboratoire d'Annecy-le-Vieux de Physique Th´eorique , Annecy Cedex, France 9Institute for Theoretical Particle Physics (TTP), Karlsruhe Institute of Technology, Kalsruhe, Germany 10Institute for Nuclear Physics (IKP), Karlsruhe Institute of Technology, Kalsruhe, Germany 11School of Physics and Astronomy, University of Birmingham, Birmingham, United Kingdom 12INFN Laboratori Nazionali di Frascati, Frascati, Italy 13Laboratoire de l'Accelerateur Lineaire (LAL), Orsay, France 14Instituto de Astrof´ısica de Canarias and Universidad de La Laguna, Departamento de Astrof´ısica, La Laguna, Tenerife, Spain 15CERN, CH-1211, Geneva 23, Switzerland 16Physik-Institut, Universit¨atZ¨urich,Z¨urich,Switzerland arXiv:1808.03477v2 [hep-ex] 31 Jul 2019 Abstract This report details the capabilities of LHCb and its upgrades towards the study of kaons and hyperons.
    [Show full text]
  • Improved Algorithms and Coupled Neutron-Photon Transport For
    Submitted to ‘Chinese Physics C’ Improved Algorithms and Coupled Neutron-Photon Transport for Auto-Importance Sampling Method * Xin Wang(王鑫)1,2 Zhen Wu(武祯)3 Rui Qiu(邱睿)1,2;1) Chun-Yan Li(李春艳)3 Man-Chun Liang(梁漫春)1 Hui Zhang(张辉) 1,2 Jun-Li Li(李君利)1,2 Zhi Gang(刚直)4 Hong Xu(徐红)4 1 Department of Engineering Physics, Tsinghua University, Beijing 100084, China 2Key Laboratory of Particle & Radiation Imaging, Ministry of Education, Beijing 100084, China 3 Nuctech Company Limited, Beijing 100084, China 4 State Nuclear Hua Qing (Beijing) Nuclear Power Technology R&D Center Co. Ltd., Beijing 102209, China Abstract: The Auto-Importance Sampling (AIS) method is a Monte Carlo variance reduction technique proposed for deep penetration problems, which can significantly improve computational efficiency without pre-calculations for importance distribution. However, the AIS method is only validated with several simple examples, and cannot be used for coupled neutron-photon transport. This paper presents improved algorithms for the AIS method, including particle transport, fictitious particle creation and adjustment, fictitious surface geometry, random number allocation and calculation of the estimated relative error. These improvements allow the AIS method to be applied to complicated deep penetration problems with complex geometry and multiple materials. A Completely coupled Neutron-Photon Auto-Importance Sampling (CNP-AIS) method is proposed to solve the deep penetration problems of coupled neutron-photon transport using the improved algorithms. The NUREG/CR-6115 PWR benchmark was calculated by using the methods of CNP-AIS, geometry splitting with Russian roulette and analog Monte Carlo, respectively.
    [Show full text]
  • 8.1 the Neutron-To-Proton Ratio
    M. Pettini: Introduction to Cosmology | Lecture 8 PRIMORDIAL NUCLEOSYNTHESIS Our discussion at the end of the previous lecture concentrated on the rela- tivistic components of the Universe, photons and leptons. Baryons (which are non-relativistic) did not figure because they make a trifling contribu- tion to the energy density. However, from t ∼ 1 s a number of nuclear reactions involving baryons took place. The end result of these reactions was to lock up most of the free neutrons into 4He nuclei and to create trace amounts of D, 3He, 7Li and 7Be. This is Primordial Nucleosynthesis, also referred to as Big Bang Nucleosynthesis (BBN). 8.1 The Neutron-to-Proton Ratio Before neutrino decoupling at around 1 MeV, neutrons and protons are kept in mutual thermal equilibrium through charged-current weak interactions: + n + e ! p +ν ¯e − p + e ! n + νe (8.1) − n ! p + e +ν ¯e While equilibrium persists, the relative number densities of neutrons and protons are given by a Boltzmann factor based on their mass difference: n ∆m c2 1:5 = exp − = exp − (8.2) p eq kT T10 where 10 ∆m = (mn − mp) = 1:29 MeV = 1:5 × 10 K (8.3) 10 and T10 is the temperature in units of 10 K. As discussed in Lecture 7.1.2, this equilibrium will be maintained so long as the timescale for the weak interactions is short compared with the timescale of the cosmic expansion (which increases the mean distance between parti- cles). In 7.2.1 we saw that the ratio of the two rates varies approximately as: Γ T 3 ' : (8.4) H 1:6 × 1010 K 1 This steep dependence on temperature can be appreciated as follows.
    [Show full text]
  • How and Why to Go Beyond the Discovery of the Higgs Boson
    How and Why to go Beyond the Discovery of the Higgs Boson John Alison University of Chicago http://hep.uchicago.edu/~johnda/ComptonLectures.html Lecture Outline April 1st: Newton’s dream & 20th Century Revolution April 8th: Mission Barely Possible: QM + SR April 15th: The Standard Model April 22nd: Importance of the Higgs April 29th: Guest Lecture May 6th: The Cannon and the Camera May 13th: The Discovery of the Higgs Boson May 20th: Problems with the Standard Model May 27th: Memorial Day: No Lecture June 3rd: Going beyond the Higgs: What comes next ? 2 Reminder: The Standard Model Description fundamental constituents of Universe and their interactions Triumph of the 20th century Quantum Field Theory: Combines principles of Q.M. & Relativity Constituents (Matter Particles) Spin = 1/2 Leptons: Quarks: νe νµ ντ u c t ( e ) ( µ) ( τ ) ( d ) ( s ) (b ) Interactions Dictated by principles of symmetry Spin = 1 QFT ⇒ Particle associated w/each interaction (Force Carriers) γ W Z g Consistent theory of electromagnetic, weak and strong forces ... ... provided massless Matter and Force Carriers Serious problem: matter and W, Z carriers have Mass ! 3 Last Time: The Higgs Feild New field (Higgs Field) added to the theory Allows massive particles while preserve mathematical consistency Works using trick: “Spontaneously Symmetry Breaking” Zero Field value Symmetric in Potential Energy not minimum Field value of Higgs Field Ground State 0 Higgs Field Value Ground state (vacuum of Universe) filled will Higgs field Leads to particle masses: Energy cost to displace Higgs Field / E=mc 2 Additional particle predicted by the theory. Higgs boson: H Spin = 0 4 Last Time: The Higgs Boson What do we know about the Higgs Particle: A Lot Higgs is excitations of v-condensate ⇒ Couples to matter / W/Z just like v X matter: e µ τ / quarks W/Z h h ~ (mass of matter) ~ (mass of W or Z) matter W/Z Spin: 0 1/2 1 3/2 2 Only thing we don’t (didn’t!) know is the value of mH 5 History of Prediction and Discovery Late 60s: Standard Model takes modern form.
    [Show full text]