DOCSLIB.ORG

Statistical Inference a Work in Progress

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Statistical Inference a Work in Progress Ronald Christensen Department of Mathematics and Statistics University of New Mexico Copyright c 2019 Statistical Inference A Work in Progress Springer v Seymour and Wes. Preface “But to us, probability is the very guide of life.” Joseph Butler (1736). The Analogy of Religion, Natural and Revealed, to the Constitution and Course of Nature, Introduction. https://www.loc.gov/resource/dcmsiabooks. analogyofreligio00butl_1/?sp=41 Normally, I wouldn’t put anything this incomplete on the internet but I wanted to make parts of it available to my Advanced Inference Class, and once it is up, you have lost control. Seymour Geisser was a mentor to Wes Johnson and me. He was Wes’s Ph.D. advisor. Near the end of his life, Seymour was finishing his 2005 book Modes of Parametric Statistical Inference and needed some help. Seymour asked Wes and Wes asked me. I had quite a few ideas for the book but then I discovered that Sey- mour hated anyone changing his prose. That was the end of my direct involvement. The first idea for this book was to revisit Seymour’s. (So far, that seems only to occur in Chapter 1.) Thinking about what Seymour was doing was the inspiration for me to think about what I had to say about statistical inference. And much of what I have to say is inspired by Seymour’s work as well as the work of my other professors at Min- nesota, notably Christopher Bingham, R. Dennis Cook, Somesh Das Gupta, Mor- ris L. Eaton, Stephen E. Fienberg, Narish Jain, F. Kinley Larntz, Frank B. Martin, Stephen Orey, William Suderth, and Sanford Weisberg. No one had a greater influ- ence on my career than my advisor, Donald A. Berry. I simply would not be where I am today if Don had not taken me under his wing. The material in this book is what I (try to) cover in the first semester of a one year course on Advanced Statistical Inference. The other semester I use Ferguson (1996). The course is for students who have had at least Advanced Calculus and hopefully some Introduction to Analysis. The course is at least as much about introducing some mathematical rigor into their studies as it is about teaching statistical inference. (Rigor also occurs in our Linear Models class but there it is in linear algebra and vii viii Preface here it is in analysis.) I try to introduce just enough measure theory for students to get an idea of its value (and to facility my presentations). But I get tired of doing analysis, so occasionally I like to teach some inference in the advanced inference course. Many years ago I went to a JSM (Joint Statistical Meeting) and heard Brian Joiner make the point that everybody learns from examples to generalities/theory. Ever since I have tried, with varying amounts of success, to incorporate this dictum into my books. (Plane Answers’ first edition preceded that experience.) This book has four chapters of example based discussion before it begins the theory in Chapter 5. There are only three chapters of theory but they are tied to extensive appendices on technical material. The first appendix merely reviews basic (non-measure theoretic) ideas of multivariate distributions. The second briefly introduces ideas of measure theory, measure theoretic probability, and convergence. Appendix C introduces the measure theoretic approaches to conditional probability and conditional expecta- tion. Appendix D adds a little depth (very little) to the discussion of measure theory and probability. Appendix E introduces the concept of identifiability. Appendix F merely reviews concepts of multivariate differentiation. Chapters 8 through 13 are me being self-indulgent and tossing in things of personal interest to me. (They don’t actually get covered in the class.) References to PA and ALM are to my books Plane Answers and Advanced Linear Modeling. Preface ix Recommended Additional Reading Ferguson, T. S. (1967). Mathematical Statistics: A Decision Theoretic Approach. Academic Press, New York. I would use this as a text if it were not out of print! I may have borrowed even more than I realized from this. Rao, C. R. (1973). Linear Statistical Inference and Its Applications, Second Edition. John Wiley and Sons, New York. Covers almost everything I want to cover. Not bad to read but I have found it impossible to teach out of. Cramer,´ H. (1946). Mathematical Methods of Statistics. Princeton University Press, Princeton. Excellent! All the analysis you need to do math stat? Limited because of age. Lehmann, E. L. (1983) Theory of Point Estimation. John Wiley and Sons, New York. (Now Lehmann and Casella.) Lehmann, E. L. (1986) Testing Statistical Hypotheses, Second Edition. John Wiley and Sons, New York. (Now Lehmann and Romano.) Berger, J. O. (1993). Statistical Decision Theory and Bayesian Analysis. Revised Second Edition. Springer-Verlag, New York. We used to teach Advanced Inference out of above three books. Cox, D. R. and Hinkley, D. V. (1974). Theoretical Statistics. Chapman and Hall, London. More profound on ideas, less on math. Manoukian, E. B. (1986), Modern Concepts and Theorems of Mathematical Statistics. Springer- Verlag, New York. SHORT! Usually the first book off my shelf. Statements, not proofs or explanations. Anderson, T. W. (2003). An Introduction to Multivariate Statistical Analysis, Third Edition. John Wiley and Sons, New York. For our purposes, a source for multivariate normal only. An alternative to PA for this. Wilks, Mathematical Statistics; Zacks, Theory of Statistical Inference. Both old but thorough. Wilks is great for order statistics and distributions related to discrete data. Wasserman, Larry (2004). All of Statistics. Springer, New York. Statistical Inference Cox, D.R. (2006). Principles of Statistical Inference. Cambridge University Press, Cambridge. Fisher, R.A. (1956). Statistical Methods and Scientific Inference, Third Edition, 1973. Hafner Press, New York. Geisser, S. (1993). Modes of Parametric Statistical Inference. Wiley, New York. Bayesian Books de Finetti, B. (1974, 1975). Theory of Probability, Vols. 1 and 2. John Wiley and Sons, New York. Jeffreys, H. (1961). Theory of Probability, Third Edition. Oxford University Press, London. Savage, L. J. (1954). The Foundations of Statistics. John Wiley and Sons, New York. DeGroot, M. H. (1970). Optimal Statistical Decisions. McGraw-Hill, New York. First three are foundational. There are now TONS of other books, see mine for other references. Large Sample Theory Books Ferguson, Thomas S. (1996). A Course in Large Sample Theory. Chapman and Hall, New York. I teach out of this. (Need I say more?) Lehmann, E. L. (1999) Elements of Large-Sample Theory. Springer. Serfling, R. J. (1980). Approximation Theorems of Mathematical Statistics, Wiley, (paperback, 2001) I haven’t read either of the last two, but I hear they are good. x Preface Probability and Measure Theory Books Ash, Robert B. and Doleans-Dade, Catherine A. (2000). Probability and Measure Theory, Second Edition. Academic Press, San Diego. I studied the first edition of this while in grad school and continue to use it as a reference. Billingsley, Patrick (2012). Probability and Measure, Fourth Edition. Wiley, New York. I haven’t read this, but I hear it is good. There are lots of others. There are also lots of good books on probability alone. Contents Preface ............................................................ vii Table of Contents ................................................... ix 1 Overview ...................................................... 1 1.1 Early Examples............................................1 1.2 Testing...................................................1 1.3 Decision Theory...........................................2 1.4 Some Ideas about Inference..................................2 1.5 The End..................................................2 1.6 The Bitter End.............................................3 2 Significance Tests .............................................. 5 2.1 Generalities...............................................5 2.2 Continuous Distributions.................................... 13 2.2.1 One Sample Normals................................. 13 2.3 Testing Two Sample Variances................................ 19 2.4 Fisher’s z distribution........................................ 21 2.5 Final Notes................................................ 27 3 Hypothesis Tests ............................................... 29 3.1 Testing Two Simple Hypotheses.............................. 29 3.1.1 Neyman-Pearson tests................................ 30 3.1.2 Bayesian Tests...................................... 33 3.2 Simple Versus Composite Hypotheses......................... 34 3.2.1 Neyman-Pearson Testing.............................. 35 3.2.2 Bayesian Testing..................................... 36 3.3 Composite versus Composite................................. 37 3.3.1 Neyman-Pearson Testing.............................. 37 3.3.2 Bayesian Testing..................................... 38 3.4 More on Neyman-Pearson Tests.............................. 38 xiii xiv Contents 3.5 More on Bayesian Testing................................... 39 3.6 Hypothesis Test P Values.................................... 40 3.7 Permutation Tests.......................................... 41 4 Comparing Testing Procedures .................................. 43 4.1 Discussion................................................ 44 4.2 Jeffreys’ Critique........................................... 46 5 Decision Theory................................................ 47 5.1 Optimal Prior Actions......................................
Load more

Recommended publications
  • F:\RSS\Me\Society's Mathemarica
    School of Social Sciences Economics Division University of Southampton Southampton SO17 1BJ, UK Discussion Papers in Economics and Econometrics Mathematics in the Statistical Society 1883-1933 John Aldrich No. 0919 This paper is available on our website http://www.southampton.ac.uk/socsci/economics/research/papers ISSN 0966-4246 Mathematics in the Statistical Society 1883-1933* John Aldrich Economics Division School of Social Sciences University of Southampton Southampton SO17 1BJ UK e-mail: [email protected] Abstract This paper considers the place of mathematical methods based on probability in the work of the London (later Royal) Statistical Society in the half-century 1883-1933. The end-points are chosen because mathematical work started to appear regularly in 1883 and 1933 saw the formation of the Industrial and Agricultural Research Section– to promote these particular applications was to encourage mathematical methods. In the period three movements are distinguished, associated with major figures in the history of mathematical statistics–F. Y. Edgeworth, Karl Pearson and R. A. Fisher. The first two movements were based on the conviction that the use of mathematical methods could transform the way the Society did its traditional work in economic/social statistics while the third movement was associated with an enlargement in the scope of statistics. The study tries to synthesise research based on the Society’s archives with research on the wider history of statistics. Key names : Arthur Bowley, F. Y. Edgeworth, R. A. Fisher, Egon Pearson, Karl Pearson, Ernest Snow, John Wishart, G. Udny Yule. Keywords : History of Statistics, Royal Statistical Society, mathematical methods.
    [Show full text]
  • Two Principles of Evidence and Their Implications for the Philosophy of Scientific Method
    TWO PRINCIPLES OF EVIDENCE AND THEIR IMPLICATIONS FOR THE PHILOSOPHY OF SCIENTIFIC METHOD by Gregory Stephen Gandenberger BA, Philosophy, Washington University in St. Louis, 2009 MA, Statistics, University of Pittsburgh, 2014 Submitted to the Graduate Faculty of the Kenneth P. Dietrich School of Arts and Sciences in partial fulfillment of the requirements for the degree of Doctor of Philosophy University of Pittsburgh 2015 UNIVERSITY OF PITTSBURGH KENNETH P. DIETRICH SCHOOL OF ARTS AND SCIENCES This dissertation was presented by Gregory Stephen Gandenberger It was defended on April 14, 2015 and approved by Edouard Machery, Pittsburgh, Dietrich School of Arts and Sciences Satish Iyengar, Pittsburgh, Dietrich School of Arts and Sciences John Norton, Pittsburgh, Dietrich School of Arts and Sciences Teddy Seidenfeld, Carnegie Mellon University, Dietrich College of Humanities & Social Sciences James Woodward, Pittsburgh, Dietrich School of Arts and Sciences Dissertation Director: Edouard Machery, Pittsburgh, Dietrich School of Arts and Sciences ii Copyright © by Gregory Stephen Gandenberger 2015 iii TWO PRINCIPLES OF EVIDENCE AND THEIR IMPLICATIONS FOR THE PHILOSOPHY OF SCIENTIFIC METHOD Gregory Stephen Gandenberger, PhD University of Pittsburgh, 2015 The notion of evidence is of great importance, but there are substantial disagreements about how it should be understood. One major locus of disagreement is the Likelihood Principle, which says roughly that an observation supports a hypothesis to the extent that the hy- pothesis predicts it. The Likelihood Principle is supported by axiomatic arguments, but the frequentist methods that are most commonly used in science violate it. This dissertation advances debates about the Likelihood Principle, its near-corollary the Law of Likelihood, and related questions about statistical practice.
    [Show full text]
  • Computing the Oja Median in R: the Package Ojanp
    Computing the Oja Median in R: The Package OjaNP Daniel Fischer Karl Mosler Natural Resources Institute of Econometrics Institute Finland (Luke) and Statistics Finland University of Cologne and Germany School of Health Sciences University of Tampere Finland Jyrki M¨ott¨onen Klaus Nordhausen Department of Social Research Department of Mathematics University of Helsinki and Statistics Finland University of Turku Finland and School of Health Sciences University of Tampere Finland Oleksii Pokotylo Daniel Vogel Cologne Graduate School Institute of Complex Systems University of Cologne and Mathematical Biology Germany University of Aberdeen United Kingdom June 27, 2016 arXiv:1606.07620v1 [stat.CO] 24 Jun 2016 Abstract The Oja median is one of several extensions of the univariate median to the mul- tivariate case. It has many nice properties, but is computationally demanding. In this paper, we first review the properties of the Oja median and compare it to other multivariate medians. Afterwards we discuss four algorithms to compute the Oja median, which are implemented in our R-package OjaNP. Besides these 1 algorithms, the package contains also functions to compute Oja signs, Oja signed ranks, Oja ranks, and the related scatter concepts. To illustrate their use, the corresponding multivariate one- and C-sample location tests are implemented. Keywords Oja median, Oja signs, Oja signed ranks, Oja ranks, R,C,C++ 1 Introduction The univariate median is a popular location estimator. It is, however, not straightforward to generalize it to the multivariate case since no generalization known retains all properties of univariate estimator, and therefore different gen- eralizations emphasize different properties of the univariate median.
    [Show full text]
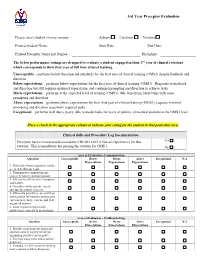
  • Third Year Preceptor Evaluation Form
    3rd Year Preceptor Evaluation Please select student’s home campus: Auburn Carolinas Virginia Printed Student Name: Start Date: End Date: Printed Preceptor Name and Degree: Discipline: The below performance ratings are designed to evaluate a student engaged in their 3rd year of clinical rotations which corresponds to their first year of full time clinical training. Unacceptable – performs below the expected standards for the first year of clinical training (OMS3) despite feedback and direction Below expectations – performs below expectations for the first year of clinical training (OMS3). Responds to feedback and direction but still requires maximal supervision, and continual prompting and direction to achieve tasks Meets expectations – performs at the expected level of training (OMS3); able to perform basic tasks with some prompting and direction Above expectations – performs above expectations for their first year of clinical training (OMS3); requires minimal prompting and direction to perform required tasks Exceptional – performs well above peers; able to model tasks for peers or juniors, of medical students at the OMS3 level Place a check in the appropriate column to indicate your rating for the student in that particular area. Clinical skills and Procedure Log Documentation Preceptor has reviewed and discussed the CREDO LOG (Clinical Experience) for this Yes rotation. This is mandatory for passing the rotation for OMS 3. No Area of Evaluation - Communication Question Unacceptable Below Meets Above Exceptional N/A Expectations Expectations Expectations 1. Effectively listen to patients, family, peers, & healthcare team. 2. Demonstrates compassion and respect in patient communications. 3. Effectively collects chief complaint and history. 4. Considers whole patient: social, spiritual & cultural concerns.
    [Show full text]
  • The Likelihood Principle
    1 01/28/99 ãMarc Nerlove 1999 Chapter 1: The Likelihood Principle "What has now appeared is that the mathematical concept of probability is ... inadequate to express our mental confidence or diffidence in making ... inferences, and that the mathematical quantity which usually appears to be appropriate for measuring our order of preference among different possible populations does not in fact obey the laws of probability. To distinguish it from probability, I have used the term 'Likelihood' to designate this quantity; since both the words 'likelihood' and 'probability' are loosely used in common speech to cover both kinds of relationship." R. A. Fisher, Statistical Methods for Research Workers, 1925. "What we can find from a sample is the likelihood of any particular value of r [a parameter], if we define the likelihood as a quantity proportional to the probability that, from a particular population having that particular value of r, a sample having the observed value r [a statistic] should be obtained. So defined, probability and likelihood are quantities of an entirely different nature." R. A. Fisher, "On the 'Probable Error' of a Coefficient of Correlation Deduced from a Small Sample," Metron, 1:3-32, 1921. Introduction The likelihood principle as stated by Edwards (1972, p. 30) is that Within the framework of a statistical model, all the information which the data provide concerning the relative merits of two hypotheses is contained in the likelihood ratio of those hypotheses on the data. ...For a continuum of hypotheses, this principle
    [Show full text]
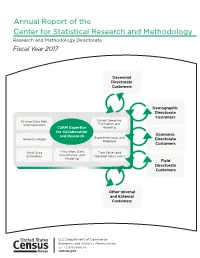
  • Annual Report of the Center for Statistical Research and Methodology Research and Methodology Directorate Fiscal Year 2017
    Annual Report of the Center for Statistical Research and Methodology Research and Methodology Directorate Fiscal Year 2017 Decennial Directorate Customers Demographic Directorate Customers Missing Data, Edit, Survey Sampling: and Imputation Estimation and CSRM Expertise Modeling for Collaboration Economic and Research Experimentation and Record Linkage Directorate Modeling Customers Small Area Simulation, Data Time Series and Estimation Visualization, and Seasonal Adjustment Modeling Field Directorate Customers Other Internal and External Customers ince August 1, 1933— S “… As the major figures from the American Statistical Association (ASA), Social Science Research Council, and new Roosevelt academic advisors discussed the statistical needs of the nation in the spring of 1933, it became clear that the new programs—in particular the National Recovery Administration—would require substantial amounts of data and coordination among statistical programs. Thus in June of 1933, the ASA and the Social Science Research Council officially created the Committee on Government Statistics and Information Services (COGSIS) to serve the statistical needs of the Agriculture, Commerce, Labor, and Interior departments … COGSIS set … goals in the field of federal statistics … (It) wanted new statistical programs—for example, to measure unemployment and address the needs of the unemployed … (It) wanted a coordinating agency to oversee all statistical programs, and (it) wanted to see statistical research and experimentation organized within the federal government … In August 1933 Stuart A. Rice, President of the ASA and acting chair of COGSIS, … (became) assistant director of the (Census) Bureau. Joseph Hill (who had been at the Census Bureau since 1900 and who provided the concepts and early theory for what is now the methodology for apportioning the seats in the U.S.
    [Show full text]
  • Point Estimation Decision Theory
    Point estimation Suppose we are interested in the value of a parameter θ, for example the unknown bias of a coin. We have already seen how one may use the Bayesian method to reason about θ; namely, we select a likelihood function p(D j θ), explaining how observed data D are expected to be generated given the value of θ. Then we select a prior distribution p(θ) reecting our initial beliefs about θ. Finally, we conduct an experiment to gather data and use Bayes’ theorem to derive the posterior p(θ j D). In a sense, the posterior contains all information about θ that we care about. However, the process of inference will often require us to use this posterior to answer various questions. For example, we might be compelled to choose a single value θ^ to serve as a point estimate of θ. To a Bayesian, the selection of θ^ is a decision, and in dierent contexts we might want to select dierent values to report. In general, we should not expect to be able to select the true value of θ, unless we have somehow observed data that unambiguously determine it. Instead, we can only hope to select an estimate that is “close” to the true value. Dierent denitions of “closeness” can naturally lead to dierent estimates. The Bayesian approach to point estimation will be to analyze the impact of our choice in terms of a loss function, which describes how “bad” dierent types of mistakes can be. We then select the estimate which appears to be the least “bad” according to our current beliefs about θ.
    [Show full text]
  • The Fire and Smoke Model Evaluation Experiment—A Plan for Integrated, Large Fire–Atmosphere Field Campaigns
    atmosphere Review The Fire and Smoke Model Evaluation Experiment—A Plan for Integrated, Large Fire–Atmosphere Field Campaigns Susan Prichard 1,*, N. Sim Larkin 2, Roger Ottmar 2, Nancy H.F. French 3 , Kirk Baker 4, Tim Brown 5, Craig Clements 6 , Matt Dickinson 7, Andrew Hudak 8 , Adam Kochanski 9, Rod Linn 10, Yongqiang Liu 11, Brian Potter 2, William Mell 2 , Danielle Tanzer 3, Shawn Urbanski 12 and Adam Watts 5 1 University of Washington School of Environmental and Forest Sciences, Box 352100, Seattle, WA 98195-2100, USA 2 US Forest Service Pacific Northwest Research Station, Pacific Wildland Fire Sciences Laboratory, Suite 201, Seattle, WA 98103, USA; [email protected] (N.S.L.); [email protected] (R.O.); [email protected] (B.P.); [email protected] (W.M.) 3 Michigan Technological University, 3600 Green Court, Suite 100, Ann Arbor, MI 48105, USA; [email protected] (N.H.F.F.); [email protected] (D.T.) 4 US Environmental Protection Agency, 109 T.W. Alexander Drive, Durham, NC 27709, USA; [email protected] 5 Desert Research Institute, 2215 Raggio Parkway, Reno, NV 89512, USA; [email protected] (T.B.); [email protected] (A.W.) 6 San José State University Department of Meteorology and Climate Science, One Washington Square, San Jose, CA 95192-0104, USA; [email protected] 7 US Forest Service Northern Research Station, 359 Main Rd., Delaware, OH 43015, USA; [email protected] 8 US Forest Service Rocky Mountain Research Station Moscow Forestry Sciences Laboratory, 1221 S Main St., Moscow, ID 83843, USA; [email protected] 9 Department of Atmospheric Sciences, University of Utah, 135 S 1460 East, Salt Lake City, UT 84112-0110, USA; [email protected] 10 Los Alamos National Laboratory, P.O.
    [Show full text]
  • Journals in Assessment, Evaluation, Measurement, Psychometrics and Statistics
    Leadership Awards Publications Resources Membership About Journals in Assessment, Evaluation, Measurement, Psychometrics and Statistics Compiled by (mailto:[email protected]) Lihshing Leigh Wang (mailto:[email protected]) , Chair of APA Division 5 Public and International Affairs Committee. Journal Association/ Scope and Aims (Adapted from journals' mission Impact Publisher statements) Factor* American Journal of Evaluation (http://www.sagepub.com/journalsProdDesc.nav? American Explores decisions and challenges related to prodId=Journal201729) Evaluation conceptualizing, designing and conducting 1.16 Association/Sage evaluations. Offers original articles about the methods, theory, ethics, politics, and practice of evaluation. Features broad, multidisciplinary perspectives on issues in evaluation relevant to education, public administration, behavioral sciences, human services, health sciences, sociology, criminology and other disciplines and professional practice fields. The American Statistician (http://amstat.tandfonline.com/loi/tas#.Vk-A2dKrRpg) American Publishes general-interest articles about current 0.98^ Statistical national and international statistical problems and Association programs, interesting and fun articles of a general nature about statistics and its applications, and the teaching of statistics. Applied Measurement in Education (http://www.tandf.co.uk/journals/titles/08957347.asp) Taylor & Francis Because interaction between the domains of 0.33 research and application is critical to the evaluation and improvement of
    [Show full text]
  • The Theory of the Design of Experiments
    The Theory of the Design of Experiments D.R. COX Honorary Fellow Nuffield College Oxford, UK AND N. REID Professor of Statistics University of Toronto, Canada CHAPMAN & HALL/CRC Boca Raton London New York Washington, D.C. C195X/disclaimer Page 1 Friday, April 28, 2000 10:59 AM Library of Congress Cataloging-in-Publication Data Cox, D. R. (David Roxbee) The theory of the design of experiments / D. R. Cox, N. Reid. p. cm. — (Monographs on statistics and applied probability ; 86) Includes bibliographical references and index. ISBN 1-58488-195-X (alk. paper) 1. Experimental design. I. Reid, N. II.Title. III. Series. QA279 .C73 2000 001.4 '34 —dc21 00-029529 CIP This book contains information obtained from authentic and highly regarded sources. Reprinted material is quoted with permission, and sources are indicated. A wide variety of references are listed. Reasonable efforts have been made to publish reliable data and information, but the author and the publisher cannot assume responsibility for the validity of all materials or for the consequences of their use. Neither this book nor any part may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying, microfilming, and recording, or by any information storage or retrieval system, without prior permission in writing from the publisher. The consent of CRC Press LLC does not extend to copying for general distribution, for promotion, for creating new works, or for resale. Specific permission must be obtained in writing from CRC Press LLC for such copying. Direct all inquiries to CRC Press LLC, 2000 N.W.
    [Show full text]
  • Statistical Theory
    Statistical Theory Prof. Gesine Reinert November 23, 2009 Aim: To review and extend the main ideas in Statistical Inference, both from a frequentist viewpoint and from a Bayesian viewpoint. This course serves not only as background to other courses, but also it will provide a basis for developing novel inference methods when faced with a new situation which includes uncertainty. Inference here includes estimating parameters and testing hypotheses. Overview • Part 1: Frequentist Statistics { Chapter 1: Likelihood, sufficiency and ancillarity. The Factoriza- tion Theorem. Exponential family models. { Chapter 2: Point estimation. When is an estimator a good estima- tor? Covering bias and variance, information, efficiency. Methods of estimation: Maximum likelihood estimation, nuisance parame- ters and profile likelihood; method of moments estimation. Bias and variance approximations via the delta method. { Chapter 3: Hypothesis testing. Pure significance tests, signifi- cance level. Simple hypotheses, Neyman-Pearson Lemma. Tests for composite hypotheses. Sample size calculation. Uniformly most powerful tests, Wald tests, score tests, generalised likelihood ratio tests. Multiple tests, combining independent tests. { Chapter 4: Interval estimation. Confidence sets and their con- nection with hypothesis tests. Approximate confidence intervals. Prediction sets. { Chapter 5: Asymptotic theory. Consistency. Asymptotic nor- mality of maximum likelihood estimates, score tests. Chi-square approximation for generalised likelihood ratio tests. Likelihood confidence regions. Pseudo-likelihood tests. • Part 2: Bayesian Statistics { Chapter 6: Background. Interpretations of probability; the Bayesian paradigm: prior distribution, posterior distribution, predictive distribution, credible intervals. Nuisance parameters are easy. 1 { Chapter 7: Bayesian models. Sufficiency, exchangeability. De Finetti's Theorem and its intepretation in Bayesian statistics. { Chapter 8: Prior distributions. Conjugate priors.
    [Show full text]
  • Research Designs for Program Evaluations
    03-McDavid-4724.qxd 5/26/2005 7:16 PM Page 79 CHAPTER 3 RESEARCH DESIGNS FOR PROGRAM EVALUATIONS Introduction 81 What Is Research Design? 83 The Origins of Experimental Design 84 Why Pay Attention to Experimental Designs? 89 Using Experimental Designs to Evaluate Programs: The Elmira Nurse Home Visitation Program 91 The Elmira Nurse Home Visitation Program 92 Random Assignment Procedures 92 The Findings 93 Policy Implications of the Home Visitation Research Program 94 Establishing Validity in Research Designs 95 Defining and Working With the Four Kinds of Validity 96 Statistical Conclusions Validity 97 Working with Internal Validity 98 Threats to Internal Validity 98 Introducing Quasi-Experimental Designs: The Connecticut Crackdown on Speeding and the Neighborhood Watch Evaluation in York, Pennsylvania 100 79 03-McDavid-4724.qxd 5/26/2005 7:16 PM Page 80 80–●–PROGRAM EVALUATION AND PERFORMANCE MEASUREMENT The Connecticut Crackdown on Speeding 101 The York Neighborhood Watch Program 104 Findings and Conclusions From the Neighborhood Watch Evaluation 105 Construct Validity 109 External Validity 112 Testing the Causal Linkages in Program Logic Models 114 Research Designs and Performance Measurement 118 Summary 120 Discussion Questions 122 References 125 03-McDavid-4724.qxd 5/26/2005 7:16 PM Page 81 Research Designs for Program Evaluations–●–81 INTRODUCTION Over the last 30 years, the field of evaluation has become increasingly diverse in terms of what is viewed as proper methods and practice. During the 1960s and into the 1970s most evaluators would have agreed that a good program evaluation should emulate social science research and, more specifically, methods should come as close to randomized experiments as possible.
    [Show full text]