Chapter 5 Statistical Inference
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

DATA COLLECTION METHODS Section III 5
AN OVERVIEW OF QUANTITATIVE AND QUALITATIVE DATA COLLECTION METHODS Section III 5. DATA COLLECTION METHODS: SOME TIPS AND COMPARISONS In the previous chapter, we identified two broad types of evaluation methodologies: quantitative and qualitative. In this section, we talk more about the debate over the relative virtues of these approaches and discuss some of the advantages and disadvantages of different types of instruments. In such a debate, two types of issues are considered: theoretical and practical. Theoretical Issues Most often these center on one of three topics: · The value of the types of data · The relative scientific rigor of the data · Basic, underlying philosophies of evaluation Value of the Data Quantitative and qualitative techniques provide a tradeoff between breadth and depth, and between generalizability and targeting to specific (sometimes very limited) populations. For example, a quantitative data collection methodology such as a sample survey of high school students who participated in a special science enrichment program can yield representative and broadly generalizable information about the proportion of participants who plan to major in science when they get to college and how this proportion differs by gender. But at best, the survey can elicit only a few, often superficial reasons for this gender difference. On the other hand, separate focus groups (a qualitative technique related to a group interview) conducted with small groups of men and women students will provide many more clues about gender differences in the choice of science majors, and the extent to which the special science program changed or reinforced attitudes. The focus group technique is, however, limited in the extent to which findings apply beyond the specific individuals included in the groups. -

Computing the Oja Median in R: the Package Ojanp
Computing the Oja Median in R: The Package OjaNP Daniel Fischer Karl Mosler Natural Resources Institute of Econometrics Institute Finland (Luke) and Statistics Finland University of Cologne and Germany School of Health Sciences University of Tampere Finland Jyrki M¨ott¨onen Klaus Nordhausen Department of Social Research Department of Mathematics University of Helsinki and Statistics Finland University of Turku Finland and School of Health Sciences University of Tampere Finland Oleksii Pokotylo Daniel Vogel Cologne Graduate School Institute of Complex Systems University of Cologne and Mathematical Biology Germany University of Aberdeen United Kingdom June 27, 2016 arXiv:1606.07620v1 [stat.CO] 24 Jun 2016 Abstract The Oja median is one of several extensions of the univariate median to the mul- tivariate case. It has many nice properties, but is computationally demanding. In this paper, we first review the properties of the Oja median and compare it to other multivariate medians. Afterwards we discuss four algorithms to compute the Oja median, which are implemented in our R-package OjaNP. Besides these 1 algorithms, the package contains also functions to compute Oja signs, Oja signed ranks, Oja ranks, and the related scatter concepts. To illustrate their use, the corresponding multivariate one- and C-sample location tests are implemented. Keywords Oja median, Oja signs, Oja signed ranks, Oja ranks, R,C,C++ 1 Introduction The univariate median is a popular location estimator. It is, however, not straightforward to generalize it to the multivariate case since no generalization known retains all properties of univariate estimator, and therefore different gen- eralizations emphasize different properties of the univariate median. -

Data Extraction for Complex Meta-Analysis (Decimal) Guide
Pedder, H. , Sarri, G., Keeney, E., Nunes, V., & Dias, S. (2016). Data extraction for complex meta-analysis (DECiMAL) guide. Systematic Reviews, 5, [212]. https://doi.org/10.1186/s13643-016-0368-4 Publisher's PDF, also known as Version of record License (if available): CC BY Link to published version (if available): 10.1186/s13643-016-0368-4 Link to publication record in Explore Bristol Research PDF-document This is the final published version of the article (version of record). It first appeared online via BioMed Central at http://systematicreviewsjournal.biomedcentral.com/articles/10.1186/s13643-016-0368-4. Please refer to any applicable terms of use of the publisher. University of Bristol - Explore Bristol Research General rights This document is made available in accordance with publisher policies. Please cite only the published version using the reference above. Full terms of use are available: http://www.bristol.ac.uk/red/research-policy/pure/user-guides/ebr-terms/ Pedder et al. Systematic Reviews (2016) 5:212 DOI 10.1186/s13643-016-0368-4 RESEARCH Open Access Data extraction for complex meta-analysis (DECiMAL) guide Hugo Pedder1*, Grammati Sarri2, Edna Keeney3, Vanessa Nunes1 and Sofia Dias3 Abstract As more complex meta-analytical techniques such as network and multivariate meta-analyses become increasingly common, further pressures are placed on reviewers to extract data in a systematic and consistent manner. Failing to do this appropriately wastes time, resources and jeopardises accuracy. This guide (data extraction for complex meta-analysis (DECiMAL)) suggests a number of points to consider when collecting data, primarily aimed at systematic reviewers preparing data for meta-analysis. -
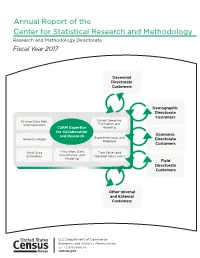
Annual Report of the Center for Statistical Research and Methodology Research and Methodology Directorate Fiscal Year 2017
Annual Report of the Center for Statistical Research and Methodology Research and Methodology Directorate Fiscal Year 2017 Decennial Directorate Customers Demographic Directorate Customers Missing Data, Edit, Survey Sampling: and Imputation Estimation and CSRM Expertise Modeling for Collaboration Economic and Research Experimentation and Record Linkage Directorate Modeling Customers Small Area Simulation, Data Time Series and Estimation Visualization, and Seasonal Adjustment Modeling Field Directorate Customers Other Internal and External Customers ince August 1, 1933— S “… As the major figures from the American Statistical Association (ASA), Social Science Research Council, and new Roosevelt academic advisors discussed the statistical needs of the nation in the spring of 1933, it became clear that the new programs—in particular the National Recovery Administration—would require substantial amounts of data and coordination among statistical programs. Thus in June of 1933, the ASA and the Social Science Research Council officially created the Committee on Government Statistics and Information Services (COGSIS) to serve the statistical needs of the Agriculture, Commerce, Labor, and Interior departments … COGSIS set … goals in the field of federal statistics … (It) wanted new statistical programs—for example, to measure unemployment and address the needs of the unemployed … (It) wanted a coordinating agency to oversee all statistical programs, and (it) wanted to see statistical research and experimentation organized within the federal government … In August 1933 Stuart A. Rice, President of the ASA and acting chair of COGSIS, … (became) assistant director of the (Census) Bureau. Joseph Hill (who had been at the Census Bureau since 1900 and who provided the concepts and early theory for what is now the methodology for apportioning the seats in the U.S. -

Reasoning with Qualitative Data: Using Retroduction with Transcript Data
Reasoning With Qualitative Data: Using Retroduction With Transcript Data © 2019 SAGE Publications, Ltd. All Rights Reserved. This PDF has been generated from SAGE Research Methods Datasets. SAGE SAGE Research Methods Datasets Part 2019 SAGE Publications, Ltd. All Rights Reserved. 2 Reasoning With Qualitative Data: Using Retroduction With Transcript Data Student Guide Introduction This example illustrates how different forms of reasoning can be used to analyse a given set of qualitative data. In this case, I look at transcripts from semi-structured interviews to illustrate how three common approaches to reasoning can be used. The first type (deductive approaches) applies pre-existing analytical concepts to data, the second type (inductive reasoning) draws analytical concepts from the data, and the third type (retroductive reasoning) uses the data to develop new concepts and understandings about the issues. The data source – a set of recorded interviews of teachers and students from the field of Higher Education – was collated by Dr. Christian Beighton as part of a research project designed to inform teacher educators about pedagogies of academic writing. Interview Transcripts Interviews, and their transcripts, are arguably the most common data collection tool used in qualitative research. This is because, while they have many drawbacks, they offer many advantages. Relatively easy to plan and prepare, interviews can be flexible: They are usually one-to one but do not have to be so; they can follow pre-arranged questions, but again this is not essential; and unlike more impersonal ways of collecting data (e.g., surveys or observation), they Page 2 of 13 Reasoning With Qualitative Data: Using Retroduction With Transcript Data SAGE SAGE Research Methods Datasets Part 2019 SAGE Publications, Ltd. -

The Theory of the Design of Experiments
The Theory of the Design of Experiments D.R. COX Honorary Fellow Nuffield College Oxford, UK AND N. REID Professor of Statistics University of Toronto, Canada CHAPMAN & HALL/CRC Boca Raton London New York Washington, D.C. C195X/disclaimer Page 1 Friday, April 28, 2000 10:59 AM Library of Congress Cataloging-in-Publication Data Cox, D. R. (David Roxbee) The theory of the design of experiments / D. R. Cox, N. Reid. p. cm. — (Monographs on statistics and applied probability ; 86) Includes bibliographical references and index. ISBN 1-58488-195-X (alk. paper) 1. Experimental design. I. Reid, N. II.Title. III. Series. QA279 .C73 2000 001.4 '34 —dc21 00-029529 CIP This book contains information obtained from authentic and highly regarded sources. Reprinted material is quoted with permission, and sources are indicated. A wide variety of references are listed. Reasonable efforts have been made to publish reliable data and information, but the author and the publisher cannot assume responsibility for the validity of all materials or for the consequences of their use. Neither this book nor any part may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying, microfilming, and recording, or by any information storage or retrieval system, without prior permission in writing from the publisher. The consent of CRC Press LLC does not extend to copying for general distribution, for promotion, for creating new works, or for resale. Specific permission must be obtained in writing from CRC Press LLC for such copying. Direct all inquiries to CRC Press LLC, 2000 N.W. -

Statistical Theory
Statistical Theory Prof. Gesine Reinert November 23, 2009 Aim: To review and extend the main ideas in Statistical Inference, both from a frequentist viewpoint and from a Bayesian viewpoint. This course serves not only as background to other courses, but also it will provide a basis for developing novel inference methods when faced with a new situation which includes uncertainty. Inference here includes estimating parameters and testing hypotheses. Overview • Part 1: Frequentist Statistics { Chapter 1: Likelihood, sufficiency and ancillarity. The Factoriza- tion Theorem. Exponential family models. { Chapter 2: Point estimation. When is an estimator a good estima- tor? Covering bias and variance, information, efficiency. Methods of estimation: Maximum likelihood estimation, nuisance parame- ters and profile likelihood; method of moments estimation. Bias and variance approximations via the delta method. { Chapter 3: Hypothesis testing. Pure significance tests, signifi- cance level. Simple hypotheses, Neyman-Pearson Lemma. Tests for composite hypotheses. Sample size calculation. Uniformly most powerful tests, Wald tests, score tests, generalised likelihood ratio tests. Multiple tests, combining independent tests. { Chapter 4: Interval estimation. Confidence sets and their con- nection with hypothesis tests. Approximate confidence intervals. Prediction sets. { Chapter 5: Asymptotic theory. Consistency. Asymptotic nor- mality of maximum likelihood estimates, score tests. Chi-square approximation for generalised likelihood ratio tests. Likelihood confidence regions. Pseudo-likelihood tests. • Part 2: Bayesian Statistics { Chapter 6: Background. Interpretations of probability; the Bayesian paradigm: prior distribution, posterior distribution, predictive distribution, credible intervals. Nuisance parameters are easy. 1 { Chapter 7: Bayesian models. Sufficiency, exchangeability. De Finetti's Theorem and its intepretation in Bayesian statistics. { Chapter 8: Prior distributions. Conjugate priors. -

Identification of Empirical Setting
Chapter 1 Identification of Empirical Setting Purpose for Identifying the Empirical Setting The purpose of identifying the empirical setting of research is so that the researcher or research manager can appropriately address the following issues: 1) Understand the type of research to be conducted, and how it will affect the design of the research investigation, 2) Establish clearly the goals and objectives of the research, and how these translate into testable research hypothesis, 3) Identify the population from which inferences will be made, and the limitations of the sample drawn for purposes of the investigation, 4) To understand the type of data obtained in the investigation, and how this will affect the ensuing analyses, and 5) To understand the limits of statistical inference based on the type of analyses and data being conducted, and this will affect final study conclusions. Inputs/Assumptions Assumed of the Investigator It is assumed that several important steps in the process of conducting research have been completed before using this part of the manual. If any of these stages has not been completed, then the researcher or research manager should first consult Volume I of this manual. 1) A general understanding of research concepts introduced in Volume I including principles of scientific inquiry and the overall research process, 2) A research problem statement with accompanying research objectives, and 3) Data or a data collection plan. Outputs/Products of this Chapter After consulting this chapter, the researcher or research -

Statistical Inference: Paradigms and Controversies in Historic Perspective
Jostein Lillestøl, NHH 2014 Statistical inference: Paradigms and controversies in historic perspective 1. Five paradigms We will cover the following five lines of thought: 1. Early Bayesian inference and its revival Inverse probability – Non-informative priors – “Objective” Bayes (1763), Laplace (1774), Jeffreys (1931), Bernardo (1975) 2. Fisherian inference Evidence oriented – Likelihood – Fisher information - Necessity Fisher (1921 and later) 3. Neyman- Pearson inference Action oriented – Frequentist/Sample space – Objective Neyman (1933, 1937), Pearson (1933), Wald (1939), Lehmann (1950 and later) 4. Neo - Bayesian inference Coherent decisions - Subjective/personal De Finetti (1937), Savage (1951), Lindley (1953) 5. Likelihood inference Evidence based – likelihood profiles – likelihood ratios Barnard (1949), Birnbaum (1962), Edwards (1972) Classical inference as it has been practiced since the 1950’s is really none of these in its pure form. It is more like a pragmatic mix of 2 and 3, in particular with respect to testing of significance, pretending to be both action and evidence oriented, which is hard to fulfill in a consistent manner. To keep our minds on track we do not single out this as a separate paradigm, but will discuss this at the end. A main concern through the history of statistical inference has been to establish a sound scientific framework for the analysis of sampled data. Concepts were initially often vague and disputed, but even after their clarification, various schools of thought have at times been in strong opposition to each other. When we try to describe the approaches here, we will use the notions of today. All five paradigms of statistical inference are based on modeling the observed data x given some parameter or “state of the world” , which essentially corresponds to stating the conditional distribution f(x|(or making some assumptions about it). -

Data Collection, Data Quality and the History of Cause-Of-Death Classifi Cation
Chapter 8 Data Collection, Data Quality and the History of Cause-of-Death Classifi cation Vladimir Shkolnikov , France Meslé , and Jacques Vallin Until 1996, when INED published its work on trends in causes of death in Russia (Meslé et al . 1996 ) , there had been no overall study of cause-specifi c mortality for the Soviet Union as a whole or for any of its constituent republics. Yet at least since the 1920s, all the republics had had a modern system for registering causes of death, and the information gathered had been subject to routine statistical use at least since the 1950s. The fi rst reason for the gap in the literature was of course that, before perestroika, these data were not published systematically and, from 1974, had even been kept secret. A second reason was probably that researchers were often ques- tioning the data quality; however, no serious study has ever proved this. On the contrary, it seems to us that all these data offer a very rich resource for anyone attempting to track and understand cause-specifi c mortality trends in the countries of the former USSR – in our case, in Ukraine. Even so, a great deal of effort was required to trace, collect and computerize the various archived data deposits. This chapter will start with a brief description of the registration system and a quick summary of the diffi culties we encountered and the data collection methods we used. We shall then review the results of some studies that enabled us to assess the quality of the data. -

Topics of Statistical Theory for Register-Based Statistics Zhang, Li-Chun Statistics Norway Kongensgt
Topics of statistical theory for register-based statistics Zhang, Li-Chun Statistics Norway Kongensgt. 6, Pb 8131 Dep N-0033 Oslo, Norway E-mail: [email protected] 1. Introduction For some decades now administrative registers have been an important data source for official statistics alongside survey sampling and population census. Not only do they provide frames and valuable auxiliary information for sample surveys and censuses, systems of inter-linked statistical registers (i.e. registers for statistical uses) have been developed on the basis of various available administrative registers to produce a wide range of purely register-based statistics (e.g. Statistics Denmark, 1995; Statistics Finland, 2004; Wallgren and Wallgren, 2007). A summary of the development of some of the key statistical registers in the Nordic countries is given in UNECE (2007, Table on page 5), the earliest ones of which came already into existence in the late 1960s and early 1970s. Statistics Denmark was the first to conduct a register-based census in 1981, and the next census in 2011 will be completely register-based in all Nordic countries. Whereas the so-called virtual census (e.g. Schulte Nordholt, 2005), which combines data from registers and various sample surveys in a more ‘traditional’ way, will be implemented in a number of European countries. The major advantages associated with the statistical use of administrative registers include reduction of response burden, long-term cost efficiency, as well as potentials for detailed spatial-demographic and longitudinal statistics. The trend towards more extensive use of administrative data has long been recognized by statisticians around the world (e.g. -

INTRODUCTION, HISTORY SUBJECT and TASK of STATISTICS, CENTRAL STATISTICAL OFFICE ¢ SZTE Mezőgazdasági Kar, Hódmezővásárhely, Andrássy Út 15
STATISTISTATISTICSCS INTRODUCTION, HISTORY SUBJECT AND TASK OF STATISTICS, CENTRAL STATISTICAL OFFICE SZTE Mezőgazdasági Kar, Hódmezővásárhely, Andrássy út 15. GPS coordinates (according to GOOGLE map): 46.414908, 20.323209 AimAim ofof thethe subjectsubject Name of the subject: Statistics Curriculum codes: EMA15121 lect , EMA151211 pract Weekly hours (lecture/seminar): (2 x 45’ lectures + 2 x 45’ seminars) / week Semester closing requirements: Lecture: exam (2 written); seminar: 2 written Credit: Lecture: 2; seminar: 1 Suggested semester : 2nd semester Pre-study requirements: − Fields of training: For foreign students Objective: Students learn and utilize basic statistical techniques in their engineering work. The course is designed to acquaint students with the basic knowledge of the rules of probability theory and statistical calculations. The course helps students to be able to apply them in practice. The areas to be acquired: data collection, information compressing, comparison, time series analysis and correlation study, reviewing the overall statistical services, land use, crop production, production statistics, price statistics and the current system of structural business statistics. Suggested literature: Abonyiné Palotás, J., 1999: Általános statisztika alkalmazása a társadalmi- gazdasági földrajzban. Use of general statistics in socio-economic geography.) JATEPress, Szeged, 123 p. Szűcs, I., 2002: Alkalmazott Statisztika. (Applied statistics.) Agroinform Kiadó, Budapest, 551 p. Reiczigel J., Harnos, A., Solymosi, N., 2007: Biostatisztika nem statisztikusoknak. (Biostatistics for non-statisticians.) Pars Kft. Nagykovácsi Rappai, G., 2001: Üzleti statisztika Excellel. (Business statistics with excel.) KSH Hunyadi, L., Vita L., 2008: Statisztika I. (Statistics I.) Aula Kiadó, Budapest, 348 p. Hunyadi, L., Vita, L., 2008: Statisztika II. (Statistics II.) Aula Kiadó, Budapest, 300 p. Hunyadi, L., Vita, L., 2008: Statisztikai képletek és táblázatok (oktatási segédlet).