DOCSLIB.ORG

The Theory of the Design of Experiments

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Theory of the Design of Experiments The Theory of the Design of Experiments D.R. COX Honorary Fellow Nuffield College Oxford, UK AND N. REID Professor of Statistics University of Toronto, Canada CHAPMAN & HALL/CRC Boca Raton London New York Washington, D.C. C195X/disclaimer Page 1 Friday, April 28, 2000 10:59 AM Library of Congress Cataloging-in-Publication Data Cox, D. R. (David Roxbee) The theory of the design of experiments / D. R. Cox, N. Reid. p. cm. — (Monographs on statistics and applied probability ; 86) Includes bibliographical references and index. ISBN 1-58488-195-X (alk. paper) 1. Experimental design. I. Reid, N. II.Title. III. Series. QA279 .C73 2000 001.4 '34 —dc21 00-029529 CIP This book contains information obtained from authentic and highly regarded sources. Reprinted material is quoted with permission, and sources are indicated. A wide variety of references are listed. Reasonable efforts have been made to publish reliable data and information, but the author and the publisher cannot assume responsibility for the validity of all materials or for the consequences of their use. Neither this book nor any part may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying, microfilming, and recording, or by any information storage or retrieval system, without prior permission in writing from the publisher. The consent of CRC Press LLC does not extend to copying for general distribution, for promotion, for creating new works, or for resale. Specific permission must be obtained in writing from CRC Press LLC for such copying. Direct all inquiries to CRC Press LLC, 2000 N.W. Corporate Blvd., Boca Raton, Florida 33431. Trademark Notice: Product or corporate names may be trademarks or registered trade- marks, and are used only for identification and explanation, without intent to infringe. Visit the CRC Press Web site at www.crcpress.com © 2000 by Chapman & Hall/CRC No claim to original U.S. Government works International Standard Book Number 1-58488-195-X Library of Congress Card Number 00-029529 Printed in the United States of America 2 3 4 5 6 7 8 9 0 Printed on acid-free paper Contents Preface 1Somegeneralconcepts 1.1Typesofinvestigation 1.2Observationalstudies 1.3Somekeyterms 1.4Requirementsindesign 1.5Interplaybetweendesignandanalysis 1.6Keystepsindesign 1.7Asimplifiedmodel 1.8Abroaderview 1.9Bibliographicnotes 1.10Furtherresultsandexercises 2Avoidanceofbias 2.1Generalremarks 2.2Randomization 2.3Retrospectiveadjustmentforbias 2.4Somemoreonrandomization 2.5Moreoncausality 2.6Bibliographicnotes 2.7Furtherresultsandexercises 3Controlofhaphazardvariation 3.1Generalremarks 3.2Precisionimprovementbyblocking 3.3Matchedpairs 3.4Randomizedblockdesign 3.5Partitioningsumsofsquares 3.6Retrospectiveadjustmentforimprovingprecision 3.7Specialmodelsoferrorvariation © 2000 by Chapman & Hall/CRC 3.8Bibliographicnotes 3.9Furtherresultsandexercises 4Specializedblockingtechniques 4.1Latinsquares 4.2Incompleteblockdesigns 4.3Cross-overdesigns 4.4Bibliographicnotes 4.5Furtherresultsandexercises 5Factorialdesigns:basicideas 5.1Generalremarks 5.2Example 5.3Maineffectsandinteractions 5.4Example:continued 5.5Twolevelfactorialsystems 5.6Fractionalfactorials 5.7Example 5.8Bibliographicnotes 5.9Furtherresultsandexercises 6Factorialdesigns:furthertopics 6.1Generalremarks 6.2Confoundingin2kdesigns 6.3Otherfactorialsystems 6.4Splitplotdesigns 6.5Nonspecificfactors 6.6Designsforquantitativefactors 6.7Taguchimethods 6.8Conclusion 6.9Bibliographicnotes 6.10Furtherresultsandexercises 7Optimaldesign 7.1Generalremarks 7.2Somesimpleexamples 7.3Somegeneraltheory 7.4Otheroptimalitycriteria 7.5Algorithmsfordesignconstruction 7.6Nonlineardesign © 2000 by Chapman & Hall/CRC 7.7Space-fillingdesigns 7.8Bayesiandesign 7.9Optimalityoftraditionaldesigns 7.10Bibliographicnotes 7.11Furtherresultsandexercises 8Someadditionaltopics 8.1Scaleofeffort 8.2Adaptivedesigns 8.3Sequentialregressiondesign 8.4Designsforone-dimensionalerrorstructure 8.5Spatialdesigns 8.6Bibliographicnotes 8.7Furtherresultsandexercises AStatisticalanalysis A.1Introduction A.2Linearmodel A.3Analysisofvariance A.4Moregeneralmodels;maximumlikelihood A.5Bibliographicnotes A.6Furtherresultsandexercises BSomealgebra B.1Introduction B.2Grouptheory B.3Galoisfields B.4Finitegeometries B.5Differencesets B.6Hadamardmatrices B.7Orthogonalarrays B.8Codingtheory B.9Bibliographicnotes B.10Furtherresultsandexercises CComputationalissues C.1Introduction C.2Overview C.3RandomizedblockexperimentfromChapter3 C.4AnalysisofblockdesignsinChapter4 © 2000 by Chapman & Hall/CRC C.5ExamplesfromChapter5 C.6ExamplesfromChapter6 C.7Bibliographicnotes References Listoftables © 2000 by Chapman & Hall/CRC Preface This book is an account of the major topics in the design of experiments, with particular emphasis on the key concepts involved and on the statistical structure associated with these concepts. While design of experiments is in many ways a very well developed area of statistics, it often receives less emphasis than methods of analysis in a programme of study in statistics. We have written for a general audience concerned with statistics in experimental fields and with some knowledge of and interest in theoretical issues. The mathematical level is mostly elementary; occasional passages using more advanced ideas can be skipped or omitted without inhibiting understanding of later passages. Some specialized parts of the subject have extensive and specialized lit- eratures, a few examples being incomplete block designs, mixture designs, designs for large variety trials, designs based on spatial stochastic models and designs constructed from explicit optimality requirements. We have aimed to give relatively brief introductions to these subjects eschewing technical detail. To motivate the discussion we give outline Illustrations taken from a range of areas of application. In addition we give a limited number of Examples, mostly taken from the literature, used for the different purpose of showing detailed methods of analysis without much emphasis on specific subject-matter interpretation. We have written a book about design not about analysis, al- though, as has often been pointed out, the two phases are inex- orably interrelated. Therefore it is, in particular, not a book on the linear statistical model or that related but distinct art form the analysis of variance table. Nevertheless these topics enter and there is a dilemma in presentation. What do we assume the reader knows about these matters? We have solved this problem uneasily by somewhat downplaying analysis in the text, by assuming what- ever is necessary for the section in question and by giving a review as an Appendix. Anyone using the book as a basis for a course of lectures will need to consider carefully what the prospective stu- dents are likely to understand about the linear model and to sup- plement the text appropriately. While the arrangement of chapters © 2000 by Chapman & Hall/CRC represents a logical progression of ideas, if interest is focused on a particular field of application it will be reasonable to omit certain parts or to take the material in a different order. If defence of a book on the theory of the subject is needed it is this. Successful application of these ideas hinges on adapting gen- eral principles to the special constraints of individual applications. Thus experience suggests that while it is useful to know about spe- cial designs, balanced incomplete block designs for instance, it is rather rare that they can be used directly. More commonly they need some adaptation to accommodate special circumstances and to do this effectively demands a solid theoretical base. This book has been developed from lectures given at Cambridge, Birkbeck College London, Vancouver, Toronto and Oxford. We are grateful to Amy Berrington, Mario Cortina Borja, Christl Don- nelly, Peter Kupchak, Rahul Mukerjee, John Nelder, Rob Tibshi- rani and especially Grace Yun Yi for helpful comments on a pre- liminary version. D.R. Cox and N. Reid Oxford and Toronto January 2000 © 2000 by Chapman & Hall/CRC List of tables 3.1Strengthindexofcotton 3.2Analysisofvarianceforstrengthindex 4.15 5Graeco-Latinsquare 4.2Co×mpleteorthogonalsetof5 5Latinsquares 4.3Balancedincompleteblockdesi×gns 4.4Twospecialincompleteblockdesigns 4.5Youdensquare 4.6Intrablockanalysisofvariance 4.7Interblockanalysisofvariance 4.8Analysisofvariance,generalincompleteblock design 4.9Logdryweightofchickbones 4.10Treatmentmeans,logdryweight 4.11Analysisofvariance,logdryweight 4.12Estimatesoftreatmenteffects 4.13Expansionindexofpastrydough 4.14Unadjustedandadjustedtreatmentmeans 4.15Exampleofintrablockanalysis 5.1Weightsofchicks 5.2Meanweightsofchicks 5.3Twofactoranalysisofvariance 5.4Analysisofvariance,weightsofchicks 5.5Decompositionoftreatmentsumofsquares 5.6Analysisofvariance,22factorial 5.7Analysisofvariance,2kfactorial 5.8Treatmentfactors,nutritionandcancer 5.9Data,nutritionandcancer 5.10Estimatedeffects,nutritionandcancer 5.11Data,Exercise5.6 5.12Contrasts,Exercise5.6 © 2000 by Chapman & Hall/CRC 6.1Example,doubleconfounding 6.2Degreesoffreedom,doubleconfounding 6.3TwoorthogonalLatinsquares 6.4Estimationofthemaineffect 6.51/3fraction,degreesoffreedom 6.6Asymmetricorthogonalarray 6.7Supersaturateddesign 6.8Example,split-plotanalysis 6.9Data,tensilestrengthofpaper 6.10Analysis,tensilestrengthofpaper 6.11Tableofmeans,tensilestrengthofpaper 6.12Analysisofvarianceforareplicatedfactorial 6.13Analysisofvariancewitharandomeffect 6.14Analysisofvariance,quality/quantityinteraction 6.15Design,electronicsexample
Load more

Recommended publications
  • Design of Experiments Application, Concepts, Examples: State of the Art
    Periodicals of Engineering and Natural Scinces ISSN 2303-4521 Vol 5, No 3, December 2017, pp. 421‒439 Available online at: http://pen.ius.edu.ba Design of Experiments Application, Concepts, Examples: State of the Art Benjamin Durakovic Industrial Engineering, International University of Sarajevo Article Info ABSTRACT Article history: Design of Experiments (DOE) is statistical tool deployed in various types of th system, process and product design, development and optimization. It is Received Aug 3 , 2018 multipurpose tool that can be used in various situations such as design for th Revised Oct 20 , 2018 comparisons, variable screening, transfer function identification, optimization th Accepted Dec 1 , 2018 and robust design. This paper explores historical aspects of DOE and provides state of the art of its application, guides researchers how to conceptualize, plan and conduct experiments, and how to analyze and interpret data including Keyword: examples. Also, this paper reveals that in past 20 years application of DOE have Design of Experiments, been grooving rapidly in manufacturing as well as non-manufacturing full factorial design; industries. It was most popular tool in scientific areas of medicine, engineering, fractional factorial design; biochemistry, physics, computer science and counts about 50% of its product design; applications compared to all other scientific areas. quality improvement; Corresponding Author: Benjamin Durakovic International University of Sarajevo Hrasnicka cesta 15 7100 Sarajevo, Bosnia Email: [email protected] 1. Introduction Design of Experiments (DOE) mathematical methodology used for planning and conducting experiments as well as analyzing and interpreting data obtained from the experiments. It is a branch of applied statistics that is used for conducting scientific studies of a system, process or product in which input variables (Xs) were manipulated to investigate its effects on measured response variable (Y).
    [Show full text]
  • Computing the Oja Median in R: the Package Ojanp
    Computing the Oja Median in R: The Package OjaNP Daniel Fischer Karl Mosler Natural Resources Institute of Econometrics Institute Finland (Luke) and Statistics Finland University of Cologne and Germany School of Health Sciences University of Tampere Finland Jyrki M¨ott¨onen Klaus Nordhausen Department of Social Research Department of Mathematics University of Helsinki and Statistics Finland University of Turku Finland and School of Health Sciences University of Tampere Finland Oleksii Pokotylo Daniel Vogel Cologne Graduate School Institute of Complex Systems University of Cologne and Mathematical Biology Germany University of Aberdeen United Kingdom June 27, 2016 arXiv:1606.07620v1 [stat.CO] 24 Jun 2016 Abstract The Oja median is one of several extensions of the univariate median to the mul- tivariate case. It has many nice properties, but is computationally demanding. In this paper, we first review the properties of the Oja median and compare it to other multivariate medians. Afterwards we discuss four algorithms to compute the Oja median, which are implemented in our R-package OjaNP. Besides these 1 algorithms, the package contains also functions to compute Oja signs, Oja signed ranks, Oja ranks, and the related scatter concepts. To illustrate their use, the corresponding multivariate one- and C-sample location tests are implemented. Keywords Oja median, Oja signs, Oja signed ranks, Oja ranks, R,C,C++ 1 Introduction The univariate median is a popular location estimator. It is, however, not straightforward to generalize it to the multivariate case since no generalization known retains all properties of univariate estimator, and therefore different gen- eralizations emphasize different properties of the univariate median.
    [Show full text]
  • Data Collection: Randomized Experiments
    9/2/15 STAT 250 Dr. Kari Lock Morgan Knee Surgery for Arthritis Researchers conducted a study on the effectiveness of a knee surgery to cure arthritis. Collecting Data: It was randomly determined whether people got Randomized Experiments the knee surgery. Everyone who underwent the surgery reported feeling less pain. SECTION 1.3 Is this evidence that the surgery causes a • Control/comparison group decrease in pain? • Clinical trials • Placebo Effect (a) Yes • Blinding • Crossover studies / Matched pairs (b) No Statistics: Unlocking the Power of Data Lock5 Statistics: Unlocking the Power of Data Lock5 Control Group Clinical Trials Clinical trials are randomized experiments When determining whether a treatment is dealing with medicine or medical interventions, effective, it is important to have a comparison conducted on human subjects group, known as the control group Clinical trials require additional aspects, beyond just randomization to treatment groups: All randomized experiments need a control or ¡ Placebo comparison group (could be two different ¡ Double-blind treatments) Statistics: Unlocking the Power of Data Lock5 Statistics: Unlocking the Power of Data Lock5 Placebo Effect Study on Placebos Often, people will experience the effect they think they should be experiencing, even if they aren’t actually Blue pills are better than yellow pills receiving the treatment. This is known as the placebo effect. Red pills are better than blue pills Example: Eurotrip 2 pills are better than 1 pill One study estimated that 75% of the
    [Show full text]
  • Design of Experiments (DOE) Using JMP Charles E
    PharmaSUG 2014 - Paper PO08 Design of Experiments (DOE) Using JMP Charles E. Shipp, Consider Consulting, Los Angeles, CA ABSTRACT JMP has provided some of the best design of experiment software for years. The JMP team continues the tradition of providing state-of-the-art DOE support. In addition to the full range of classical and modern design of experiment approaches, JMP provides a template for Custom Design for specific requirements. The other choices include: Screening Design; Response Surface Design; Choice Design; Accelerated Life Test Design; Nonlinear Design; Space Filling Design; Full Factorial Design; Taguchi Arrays; Mixture Design; and Augmented Design. Further, sample size and power plots are available. We give an introduction to these methods followed by a few examples with factors. BRIEF HISTORY AND BACKGROUND From early times, there has been a desire to improve processes with controlled experimentation. A famous early experiment cured scurvy with seamen taking citrus fruit. Lives were saved. Thomas Edison invented the light bulb with many experiments. These experiments depended on trial and error with no software to guide, measure, and refine experimentation. Japan led the way with improving manufacturing—Genichi Taguchi wanted to create repeatable and robust quality in manufacturing. He had been taught management and statistical methods by William Edwards Deming. Deming taught “Plan, Do, Check, and Act”: PLAN (design) the experiment; DO the experiment by performing the steps; CHECK the results by testing information; and ACT on the decisions based on those results. In America, other pioneers brought us “Total Quality” and “Six Sigma” with “Design of Experiments” being an advanced methodology.
    [Show full text]
  • Application of a Central Composite Design for the Study of Nox Emission Performance of a Low Nox Burner
    Energies 2015, 8, 3606-3627; doi:10.3390/en8053606 OPEN ACCESS energies ISSN 1996-1073 www.mdpi.com/journal/energies Article Application of a Central Composite Design for the Study of NOx Emission Performance of a Low NOx Burner Marcin Dutka 1,*, Mario Ditaranto 2,† and Terese Løvås 1,† 1 Department of Energy and Process Engineering, Norwegian University of Science and Technology, Kolbjørn Hejes vei 1b, Trondheim 7491, Norway; E-Mail: [email protected] 2 SINTEF Energy Research, Sem Sælands vei 11, Trondheim 7034, Norway; E-Mail: [email protected] † These authors contributed equally to this work. * Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel.: +47-41174223. Academic Editor: Jinliang Yuan Received: 24 November 2014 / Accepted: 22 April 2015 / Published: 29 April 2015 Abstract: In this study, the influence of various factors on nitrogen oxides (NOx) emissions of a low NOx burner is investigated using a central composite design (CCD) approach to an experimental matrix in order to show the applicability of design of experiments methodology to the combustion field. Four factors have been analyzed in terms of their impact on NOx formation: hydrogen fraction in the fuel (0%–15% mass fraction in hydrogen-enriched methane), amount of excess air (5%–30%), burner head position (20–25 mm from the burner throat) and secondary fuel fraction provided to the burner (0%–6%). The measurements were performed at a constant thermal load equal to 25 kW (calculated based on lower heating value). Response surface methodology and CCD were used to develop a second-degree polynomial regression model of the burner NOx emissions.
    [Show full text]
  • THE HISTORY and DEVELOPMENT of STATISTICS in BELGIUM by Dr
    THE HISTORY AND DEVELOPMENT OF STATISTICS IN BELGIUM By Dr. Armand Julin Director-General of the Belgian Labor Bureau, Member of the International Statistical Institute Chapter I. Historical Survey A vigorous interest in statistical researches has been both created and facilitated in Belgium by her restricted terri- tory, very dense population, prosperous agriculture, and the variety and vitality of her manufacturing interests. Nor need it surprise us that the successive governments of Bel- gium have given statistics a prominent place in their affairs. Baron de Reiffenberg, who published a bibliography of the ancient statistics of Belgium,* has given a long list of docu- ments relating to the population, agriculture, industry, commerce, transportation facilities, finance, army, etc. It was, however, chiefly the Austrian government which in- creased the number of such investigations and reports. The royal archives are filled to overflowing with documents from that period of our history and their very over-abun- dance forms even for the historian a most diflScult task.f With the French domination (1794-1814), the interest for statistics did not diminish. Lucien Bonaparte, Minister of the Interior from 1799-1800, organized in France the first Bureau of Statistics, while his successor, Chaptal, undertook to compile the statistics of the departments. As far as Belgium is concerned, there were published in Paris seven statistical memoirs prepared under the direction of the prefects. An eighth issue was not finished and a ninth one * Nouveaux mimoires de I'Acadimie royale des sciences et belles lettres de Bruxelles, t. VII. t The Archives of the kingdom and the catalogue of the van Hulthem library, preserved in the Biblioth^que Royale at Brussells, offer valuable information on this head.
    [Show full text]
  • Recommendations for Design Parameters for Central Composite Designs with Restricted Randomization
    Recommendations for Design Parameters for Central Composite Designs with Restricted Randomization Li Wang Dissertation submitted to the Faculty of the Virginia Polytechnic Institute and State University in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Statistics Geoff Vining, Chair Scott Kowalski, Co-Chair John P. Morgan Dan Spitzner Keying Ye August 15, 2006 Blacksburg, Virginia Keywords: Response Surface Designs, Central Composite Design, Split-plot Designs, Rotatability, Orthogonal Blocking. Copyright 2006, Li Wang Recommendations for Design Parameters for Central Composite Designs with Restricted Randomization Li Wang ABSTRACT In response surface methodology, the central composite design is the most popular choice for fitting a second order model. The choice of the distance for the axial runs, α, in a central composite design is very crucial to the performance of the design. In the literature, there are plenty of discussions and recommendations for the choice of α, among which a rotatable α and an orthogonal blocking α receive the greatest attention. Box and Hunter (1957) discuss and calculate the values for α that achieve rotatability, which is a way to stabilize prediction variance of the design. They also give the values for α that make the design orthogonally blocked, where the estimates of the model coefficients remain the same even when the block effects are added to the model. In the last ten years, people have begun to realize the importance of a split-plot structure in industrial experiments. Constructing response surface designs with a split-plot structure is a hot research area now. In this dissertation, Box and Hunters’ choice of α for rotatablity and orthogonal blocking is extended to central composite designs with a split-plot structure.
    [Show full text]
  • This History of Modern Mathematical Statistics Retraces Their Development
    BOOK REVIEWS GORROOCHURN Prakash, 2016, Classic Topics on the History of Modern Mathematical Statistics: From Laplace to More Recent Times, Hoboken, NJ, John Wiley & Sons, Inc., 754 p. This history of modern mathematical statistics retraces their development from the “Laplacean revolution,” as the author so rightly calls it (though the beginnings are to be found in Bayes’ 1763 essay(1)), through the mid-twentieth century and Fisher’s major contribution. Up to the nineteenth century the book covers the same ground as Stigler’s history of statistics(2), though with notable differences (see infra). It then discusses developments through the first half of the twentieth century: Fisher’s synthesis but also the renewal of Bayesian methods, which implied a return to Laplace. Part I offers an in-depth, chronological account of Laplace’s approach to probability, with all the mathematical detail and deductions he drew from it. It begins with his first innovative articles and concludes with his philosophical synthesis showing that all fields of human knowledge are connected to the theory of probabilities. Here Gorrouchurn raises a problem that Stigler does not, that of induction (pp. 102-113), a notion that gives us a better understanding of probability according to Laplace. The term induction has two meanings, the first put forward by Bacon(3) in 1620, the second by Hume(4) in 1748. Gorroochurn discusses only the second. For Bacon, induction meant discovering the principles of a system by studying its properties through observation and experimentation. For Hume, induction was mere enumeration and could not lead to certainty. Laplace followed Bacon: “The surest method which can guide us in the search for truth, consists in rising by induction from phenomena to laws and from laws to forces”(5).
    [Show full text]
  • Chapter 4: Fisher's Exact Test in Completely Randomized Experiments
    1 Chapter 4: Fisher’s Exact Test in Completely Randomized Experiments Fisher (1925, 1926) was concerned with testing hypotheses regarding the effect of treat- ments. Specifically, he focused on testing sharp null hypotheses, that is, null hypotheses under which all potential outcomes are known exactly. Under such null hypotheses all un- known quantities in Table 4 in Chapter 1 are known–there are no missing data anymore. As we shall see, this implies that we can figure out the distribution of any statistic generated by the randomization. Fisher’s great insight concerns the value of the physical randomization of the treatments for inference. Fisher’s classic example is that of the tea-drinking lady: “A lady declares that by tasting a cup of tea made with milk she can discriminate whether the milk or the tea infusion was first added to the cup. ... Our experi- ment consists in mixing eight cups of tea, four in one way and four in the other, and presenting them to the subject in random order. ... Her task is to divide the cups into two sets of 4, agreeing, if possible, with the treatments received. ... The element in the experimental procedure which contains the essential safeguard is that the two modifications of the test beverage are to be prepared “in random order.” This is in fact the only point in the experimental procedure in which the laws of chance, which are to be in exclusive control of our frequency distribution, have been explicitly introduced. ... it may be said that the simple precaution of randomisation will suffice to guarantee the validity of the test of significance, by which the result of the experiment is to be judged.” The approach is clear: an experiment is designed to evaluate the lady’s claim to be able to discriminate wether the milk or tea was first poured into the cup.
    [Show full text]
  • Effect of Design Selection on Response Surface Performance
    NASA Contractor Report 4520 Effect of Design Selection on Response Surface Performance William C. Carpenter University of South Florida Tampa, Florida Prepared for Langley Research Center under Grant NAG1-1378 National Aeronautics and Space Administration Office of Management Scientific and Technical Information Program 1993 Table of Contents lo Introduction ................................................. 1 1.10uality Qf Fit ............................................. 2 1.].1 Fit at the designs .................................... 2 1.1.2 Overall fit ......................................... 3 1.2. Polynomial Approximations .................................. 4 1.2.1 Exactly-determined approximation ....................... 5 1.2.2 Over-determined approximation ......................... 5 1.2.3 Under-determined approximation ........................ 6 1,3 Artificial Neural Nets ....................................... 7 1 Levels of Designs ............................................. 1O 2.1 Taylor Series Approximation ................................. 10 2,2 Example ................................................ 13 2.3 Conclu_iQn .............................................. 18 B Standard Designs ............................................ 19 3.1 Underlying Principle ....................................... 19 3.2 Statistical Concepts ....................................... 20 3.30rthogonal Designs ........................................ 23 ........................................... 24 3.3.1.1 Example of Scaled Designs: ....................
    [Show full text]
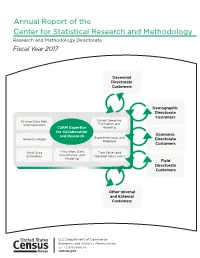
  • Annual Report of the Center for Statistical Research and Methodology Research and Methodology Directorate Fiscal Year 2017
    Annual Report of the Center for Statistical Research and Methodology Research and Methodology Directorate Fiscal Year 2017 Decennial Directorate Customers Demographic Directorate Customers Missing Data, Edit, Survey Sampling: and Imputation Estimation and CSRM Expertise Modeling for Collaboration Economic and Research Experimentation and Record Linkage Directorate Modeling Customers Small Area Simulation, Data Time Series and Estimation Visualization, and Seasonal Adjustment Modeling Field Directorate Customers Other Internal and External Customers ince August 1, 1933— S “… As the major figures from the American Statistical Association (ASA), Social Science Research Council, and new Roosevelt academic advisors discussed the statistical needs of the nation in the spring of 1933, it became clear that the new programs—in particular the National Recovery Administration—would require substantial amounts of data and coordination among statistical programs. Thus in June of 1933, the ASA and the Social Science Research Council officially created the Committee on Government Statistics and Information Services (COGSIS) to serve the statistical needs of the Agriculture, Commerce, Labor, and Interior departments … COGSIS set … goals in the field of federal statistics … (It) wanted new statistical programs—for example, to measure unemployment and address the needs of the unemployed … (It) wanted a coordinating agency to oversee all statistical programs, and (it) wanted to see statistical research and experimentation organized within the federal government … In August 1933 Stuart A. Rice, President of the ASA and acting chair of COGSIS, … (became) assistant director of the (Census) Bureau. Joseph Hill (who had been at the Census Bureau since 1900 and who provided the concepts and early theory for what is now the methodology for apportioning the seats in the U.S.
    [Show full text]
  • Concepts Underlying the Design of Experiments
    Concepts Underlying the Design of Experiments March 2000 University of Reading Statistical Services Centre Biometrics Advisory and Support Service to DFID Contents 1. Introduction 3 2. Specifying the objectives 5 3. Selection of treatments 6 3.1 Terminology 6 3.2 Control treatments 7 3.3 Factorial treatment structure 7 4. Choosing the sites 9 5. Replication and levels of variation 10 6. Choosing the blocks 12 7. Size and shape of plots in field experiments 13 8. Allocating treatment to units 14 9. Taking measurements 15 10. Data management and analysis 17 11. Taking design seriously 17 © 2000 Statistical Services Centre, The University of Reading, UK 1. Introduction This guide describes the main concepts that are involved in designing an experiment. Its direct use is to assist scientists involved in the design of on-station field trials, but many of the concepts also apply to the design of other research exercises. These range from simulation exercises, and laboratory studies, to on-farm experiments, participatory studies and surveys. What characterises the design of on-station experiments is that the researcher has control of the treatments to apply and the units (plots) to which they will be applied. The results therefore usually provide a detailed knowledge of the effects of the treat- ments within the experiment. The major limitation is that they provide this information within the artificial "environment" of small plots in a research station. A laboratory study should achieve more precision, but in a yet more artificial environment. Even more precise is a simulation model, partly because it is then very cheap to collect data.
    [Show full text]