DOCSLIB.ORG

Utilizing Distributions of Variable Influence for Feature Selection In

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Utilizing Distributions of Variable Influence for Feature Selection In UTILIZING DISTRIBUTIONS OF VARIABLE INFLUENCE FOR FEATURE SELECTION IN HYPERSPECTRAL IMAGES by Neil Stewart Walton A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science in Computer Science MONTANA STATE UNIVERSITY Bozeman, Montana April 2019 c COPYRIGHT by Neil Stewart Walton 2019 All Rights Reserved ii DEDICATION To my wonderful, supportive parents for encouraging me every step of the way, to my fantastic friends for keeping me sane and smiling through it all, and to my enigmatic brother for reasons that are as of yet still unclear to me. iii ACKNOWLEDGEMENTS I would like thank the members of the Numerical Intelligent Systems Laboratory at Montana State University | in particular, Jacob Senecal, with whom I collabo- rated on much of the research included herein, Amy Peerlinck and Jordan Schupbach for many enlightening conversations, the members of my thesis committee | Dr. David L. Millman and Dr. Joseph A. Shaw, members of the Optical Technology Center at Montana State University | especially Bryan Scherrer and Riley Logan, and, above all, my advisor and committee chair, Dr. John W. Sheppard. I would also like to thank Intel Corporation for providing funding for much of this research. iv TABLE OF CONTENTS 1. INTRODUCTION ........................................................................................1 2. BACKGROUND...........................................................................................6 2.1 Feature Selection .....................................................................................6 2.1.1 Applications to Hyperspectral Data ..................................................7 2.2 Hyperspectral Imaging.............................................................................9 2.2.1 Overview.........................................................................................9 2.2.2 Multispectral Imaging.................................................................... 10 2.2.3 Hyperspectral Produce Monitoring ................................................. 13 2.3 Genetic Algorithm ................................................................................. 14 2.3.1 General formulation....................................................................... 14 2.3.2 Fitness Function............................................................................ 16 2.3.3 Selection ....................................................................................... 17 2.3.4 Crossover ...................................................................................... 18 2.3.5 Mutation....................................................................................... 19 2.3.6 Replacement.................................................................................. 20 2.4 Artificial Neural Networks...................................................................... 21 2.5 Decision Trees ....................................................................................... 26 2.5.1 Random Forests............................................................................. 28 3. GENETIC ALGORITHM BASED FEATURE SELECTION.........................30 3.1 Related Work ........................................................................................ 30 3.2 Genetic Algorithm Formulation .............................................................. 31 3.2.1 Representation .............................................................................. 31 3.2.2 Fitness Function............................................................................ 32 3.3 Histogram-based Approach..................................................................... 32 3.3.1 Overview....................................................................................... 32 3.3.2 Hierarchical Agglomerative Clustering............................................. 33 3.3.3 Expectation-Maximization.............................................................. 37 3.3.4 Selecting Features.......................................................................... 39 3.3.5 The HAGRID Algorithm................................................................ 39 3.4 Experimental Setup and Methods ........................................................... 39 3.4.1 Hyperspectral Imaging and Staging................................................. 40 3.4.2 Data ............................................................................................. 42 3.4.2.1 Avocado and Tomato Dataset:................................................ 42 3.4.2.2 Kochia Dataset:..................................................................... 43 3.4.2.3 Indian Pines Dataset:............................................................. 44 3.4.3 Experimental Design...................................................................... 44 v TABLE OF CONTENTS { CONTINUED 3.4.4 Parameter Settings ........................................................................ 46 3.5 Experimental Results............................................................................. 47 3.6 Conclusions and Future Work................................................................. 51 4. BANDWIDTH DETERMINATION.............................................................55 4.1 Specifying Bandwidths with HAGRID .................................................... 56 4.1.1 Transforming Data ........................................................................ 57 4.2 Experimental Setup ............................................................................... 59 4.3 Experimental Results............................................................................. 61 4.4 Conclusions and Future Work................................................................. 65 5. VARIABLE INFLUENCE ALGORITHMS...................................................67 5.1 Distribution-based Feature Selection using Variable Importance ............... 67 5.1.1 Mean Decrease Accuracy................................................................ 67 5.1.2 Mean Decrease Gini....................................................................... 68 5.1.3 Related Work ................................................................................ 68 5.1.4 Multicollinearity in Hyperspectral Data .......................................... 69 5.1.5 VI-DFS......................................................................................... 71 5.2 Automated Determination of Feature Subset Size .................................... 76 5.3 Layer-wise Relevance Propagation for Feature Selection ........................... 77 5.3.1 Gradient-based Explanation ........................................................... 77 5.3.2 Layer-wise Relevance Propagation .................................................. 80 5.3.3 Applications.................................................................................. 83 5.3.4 LRP-DFS...................................................................................... 83 5.4 Experimental Setup ............................................................................... 86 5.5 Experimental Results............................................................................. 88 5.6 Conclusions and Future Work................................................................. 91 6. CONCLUSION...........................................................................................93 REFERENCES CITED....................................................................................98 APPENDIX: Wavelength and Bandwidth Settings ........................................... 109 vi LIST OF TABLES Table Page 3.1 Sample sizes for produce data sets showing number of each fruit and number of samples per fruit.................................... 43 3.2 Classification accuracy using RGB, RGB+NIR, all wavelengths, and feature selection for the avocado and tomato datasets. The best accuracy for each dataset is shown in bold. ................................................................. 49 3.3 Classification accuracies for the kochia dataset. The best results are shown in bold. ......................................................... 51 3.4 Classification accuracies for the Indian Pines dataset. The best results (excluding all wavelengths) are shown in bold. ................................................................................ 52 4.1 Wavelength centers and bandwidths for red, blue, green, and near infrared filters used in experiments. .......................... 60 4.2 Classification accuracy for the avocado and tomato datasets using various wavelength centers and sim- ulated filter bandwidths. The best results for each dataset are shown in bold. ............................................................... 63 4.3 Classification accuracy for the kochia dataset us- ing various wavelength centers and simulated filter bandwidths. The best results are shown in bold................................ 64 5.1 Wavelengths selected by VI-DFS, rank-based feature selection (VI-R), forward selection (VI-FS), and backward elimination (VI-BE) for the avocado and tomato datasets. The number of features for VI-DFS is selected automatically using BIC and the other methods were made to select that same number of features. ......................................................................................... 75 5.2 Results for the VI-DFS, LRPZ+-DFS, and LRPZB- DFS algorithms for the avocado and tomato datasets. The highest accuracy attained for each dataset is shown in bold. ...............................................................................
Load more

Recommended publications
  • 18Th International Multidisciplinary Scientific Geoconference (SGEM
    18th International Multidisciplinary Scientific GeoConference (SGEM 2018) Conference Proceedings Volume 18 Albena, Bulgaria 2 - 8 July 2018 Issue 1.1, Part A ISBN: 978-1-5108-7357-5 1/26 Printed from e-media with permission by: Curran Associates, Inc. 57 Morehouse Lane Red Hook, NY 12571 Some format issues inherent in the e-media version may also appear in this print version. Copyright© (2018) by International Multidisciplinary Scientific GeoConferences (SGEM) All rights reserved. Printed by Curran Associates, Inc. (2019) For permission requests, please contact International Multidisciplinary Scientific GeoConferences (SGEM) at the address below. International Multidisciplinary Scientific GeoConferences (SGEM) 51 Alexander Malinov Blvd. fl 4, Office B5 1712 Sofia, Bulgaria Phone: +359 2 405 18 41 Fax: +359 2 405 18 65 [email protected] Additional copies of this publication are available from: Curran Associates, Inc. 57 Morehouse Lane Red Hook, NY 12571 USA Phone: 845-758-0400 Fax: 845-758-2633 Email: [email protected] Web: www.proceedings.com Contents CONFERENCE PROCEEDINGS CONTENTS GEOLOGY 1. A PRELIMINARY EVALUATION OF BULDAN COALS (DENIZLI/WESTERN TURKEY) USING PYROLYSIS AND ORGANIC PETROGRAPHIC INVESTIGATIONS, Assoc. Prof. Dr. Demet Banu KORALAY, Zuhal Gedik VURAL, Pamukkale University, Turkey ..................................................... 3 2. ANCIENT MIDDLE-CARBONIFEROUS FLORA OF THE ORULGAN RANGE (NORTHERN VERKHOYANSK) AND JUSTIFICATION OF AGE BYLYKAT FORMATION, Mr. A.N. Kilyasov, Diamond and Precious Metal Geology Institute, Siberian Branch of the Russian Academy of Sciences (DPMGI SB RAS), Russia ................................................................................................................... 11 3. BARIUM PHLOGOPITE FROM KIMBERLITE PIPES OF CENTRAL YAKUTIA, Nikolay Oparin, Ph.D. Oleg Oleinikov, Institute of Geology of Diamond and Noble Metals SB RAS, Russia ................................................................................
    [Show full text]
  • STATE RECORDKEEPING in the CLOUD Lorraine L. Richards A
    EVIDENCE-AS-A-SERVICE: STATE RECORDKEEPING IN THE CLOUD Lorraine L. Richards A dissertation submitted to the faculty of the University of North Carolina at Chapel Hill in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the School Information and Library Science. Chapel Hill 2014 Approved by: Christopher A. Lee Helen R. Tibbo Richard Marciano Jeffrey Pomerantz Theresa A. Pardo © 2014 Lorraine L. Richards ALL RIGHTS RESERVED ii ABSTRACT Lorraine L. Richards: Evidence-as-a-Service: State Recordkeeping in the Cloud (Under the Direction of Christopher A. Lee) The White House has engaged in recent years in efforts to ensure greater citizen access to government information and greater efficiency and effectiveness in managing that information. The Open Data policy and recent directives requiring that federal agencies create capacity to share scientific data have fallen on the heels of the Federal Government’s “Cloud First” policy, an initiative requiring Federal agencies to consider using cloud computing before making IT investments. Still, much of the information accessed by the public resides in the hands of state and local records creators. Thus, this exploratory study sought to examine how cloud computing actually affects public information recordkeeping stewards. Specifically, it investigated whether recordkeeping stewards’ concerns about cloud computing risks are similar to published risks in newly implemented cloud computing environments, it examined their perceptions of how cross-occupational relationships affect their ability to perform recordkeeping responsibilities in the Cloud, and it compared how recordkeeping roles and responsibilities are distributed within their organizations. The distribution was compared to published reports of recordkeeping roles and responsibilities in archives and records management journals published over the past 42 years.
    [Show full text]
  • Temas E Sessões Internas
    ACTAS DE BIOQUÍMICA VOLUME 5 TEMAS E SESSÕES INTERNAS Editors J. Martins e Silva Carlota Saldanha 1991 “Actas de Bioquímica ” is primarily concerned with the publication of complete transcripts of the lectures, conferences and other studies presented in Advanced Post-Graduate Courses or in Scientific Symposia organized or co-organized by the Instituto de Bioquímica, Faculdade de Medicina da Universidade de Lisboa. Original or review articles and other scientific contributions in askin fields may also be included. Editors J. Martins e Silva Carlota Saldanha Editorial Office Instituto de Bioquímica, Faculdade de Medicina da Universidade de Lisboa Av. Prof. Egas Moniz Lisboa – Portugal Mailing Address Actas de Bioquímica Apartado 4098 1500-001 Lisboa – Portugal Subscription Information Subscription price is $25.00 (twenty five US dollars) (twenty euros) per volume. An additional charge of $5,00 per volume is requested for post delivery outside Portugal. Payment should accompany all orders. Correspondence concerning subscription should be addressed to the mailing address above. ISBN: 972-590-076-6 Copyrigh@ 1991 by Instituto de Bioquímica, Faculdade de Medicina da Universidade de Lisboa. All rights reserved. Printed in Portugal II ACTAS DE BIOQUÍMICA VOLUME 5 1991 ÍNDICE PREFÁCIO .................................................................................................................................................................................................................................................... V ARTIGOS Liposomes
    [Show full text]
  • Tackling Racism Seriously
    Institut de Drets Humans / Facultat de Dret Doctor’s degree in Human rights, democracy and international justice TACKLING RACISM SERIOUSLY HUMAN RIGHTS AND THE UNDERPINNINGS OF ETHNIC RECOGNITION Doctoral thesis Author Supervisor Pier-Luc Dupont Ángeles Solanes Corella València, May 2017 Because they are rational creatures, sailors go to sea with the calculations already done; and all rational creatures go out on the sea of life with their minds made up on the common questions of right and wrong, as well as on many of the much harder questions of wise and foolish. And we can presume that they will continue to do so long as foresight continues to be a human quality. Whatever we adopt as the fundamental principle of morality, we need subordinate principles through which to apply it. John Stuart Mill It is important to be quite careful before seeing any tension between equality and liberty. Tension exists only when we specify conceptions of these broad terms that cannot peacefully coexist. Perhaps such incompatible conceptions cannot be defended. Perhaps the best conceptions of equality are entirely compatible with the best understandings of liberty. Cass Sunstein Neither in interpreting statutes nor precedents are judges confined to the alternatives of blind, arbitrary choice, or ‘mechanical’ deduction from rules with predetermined meaning. Very often their choice is guided by an assumption that the purpose of the rules which they are interpreting is a reasonable one, so that the rules are not intended to work injustice or offend settled moral principles. HLA Hart Rights is the child of law; from real law come real right; but from imaginary laws, from ‘laws of nature’, come imaginary rights… Natural rights is simple nonsense […], nonsense upon stilts.
    [Show full text]
  • Classification Report
    Chess ISAS Classification Report Classification Report created by IBSA Sport Administration System Sport: Chess | Selection: Complete Database Indonesia ID Family Name Given Name Gender Birth Class Status Year of Review 26192 Setiawan Wahyu Male 1900-01-01 B1 Review 26193 Sujarwo Male 1900-01-01 B2 Review Kazakhstan ID Family Name Given Name Gender Birth Class Status Year of Review 26194 Bolat Zhanymkhan Male 1900-01-01 B2 Review 26195 Kurmashev Batyrkhan Male 1900-01-01 B3 Review Malaysia ID Family Name Given Name Gender Birth Class Status Year of Review 26205 Ahmad Shaifuddin Amirul Shafiq Male 1900-01-01 NE Review 26196 Ang Ping Ting Female 1900-01-01 B3 Review 26210 Azlan Hamzah Khoyum Male 1900-01-01 B2 Review 26206 Azmi Mohamad Fairus Male 1900-01-01 B1 Review 26197 Che Ibrahim Azril Female 1900-01-01 B1 Review 26198 Jafri Noramyliya Natasha Female 1900-01-01 B2 Review 26207 Jamil Mohamad Farhan Shukry Male 1900-01-01 B2 Review 26199 Lean Yew Lin Female 1900-01-01 B1 Review 26208 Mohamad Ali Muhamad Ikhyaul Hakim Male 1900-01-01 B2 Review 26200 Mohamed Halil Nur Feiqha Female 1900-01-01 B2 Review 26201 Mohd Rasdi Mohd Zahir Female 1900-01-01 B2 Review 26202 Muhd Soberi Seri Idzihar Female 1900-01-01 B3 Review 26203 Sulaiman Safiah Female 1900-01-01 B2 Review 26204 Tan Chin Ning Female 1900-01-01 B3 Review IBSA Sport Administration System Page 1 of 2 Timestamp 2015-02-10 14:51:20 Chess ISAS Classification Report 26209 Watson Manda Edwin Male 1900-01-01 B3 Review Romania ID Family Name Given Name Gender Birth Class Status Year of Review
    [Show full text]
  • A Bibliography of Geomorphometry, the Quantitative Representation of Topography Supplement 2.0
    U.S. DEPARTMENT OF THE INTERIOR U.S. GEOLOGICAL SURVEY A Bibliography of Geomorphometry, the Quantitative Representation of Topography Supplement 2.0 By RICHARD J. PIKE 1 Provides over 800 additions and corrections to the 1993 Bibliography of Geomorphometry and its 1995 Supplement 1.0, with a brief update on recent advances OPEN-FILE REPORT 96-726 1996 This report is preliminary and has not been reviewed for conformity with U.S. Geological Survey editorial standards or with the North American Stratigraphic Code. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government PARK, CA 94025 A Bibliography of Geomorphometry, the Quantitative Representation of Topography Supplement 2.0 by Richard J. Pike Abstract This report adds more than 800 references on the numerical characterization of topography (geomorphometry) to a 1993 review of the literature and its 1995 supplement. Several corrections are included. The report also briefly reviews four recent advances and related topics: fractal modeling of fluvial networks, new sources of digital data (emphasizing Internet access), industrial micro-surface metrology, and morphometry in Japan. he rapid growth of terrain first supplement, which was current through quantification continues through its mid-1994. Coverage is inclusive, but not T many applications in geomorphology, exhaustive. hydrology, geohazards mapping, and land- use evaluation. Geomorphometry (or simply The appended listing is alphabetized and morphometry) is an amalgam of Earth unannotated, following the format of its two science, mathematics, engineering, and predecessors. The 60-topic organization of computer science; it is known variously as geomorphometry developed initially (Pike, terrain modeling, terrain analysis, and 1993, Table 2) and later revised (Pike, 1995a, quantitative geomorphology.
    [Show full text]
  • Palestrica of the Third Millennium - Civilization and Sport
    PALESTRICA OF THE THIRD MILLENNIUM - CIVILIZATION AND SPORT A quarterly of multidisciplinary study and research © Published by The “Iuliu Haţieganu” University of Medicine and Pharmacy of Cluj-Napoca and The Romanian Medical Society of Physical Education and Sports in collaboration with The Cluj County School Inspectorate A journal rated B+ by CNCS (Romanian National Research Council) since 2007, certified by CMR (Romanian College of Physicians) since 2003 and CFR (Romanian College of Pharmacists) since 2015 A journal with a multidisciplinary approach in the fields of biomedical science, health, medical rehabilitation, physical exercise, social sciences applied to physical education and sports activities A journal indexed in international databases: EBSCO, Academic Search Complete, USA; Index Copernicus, Journals Master List, Poland; DOAJ (Directory of Open Access Journals), Sweden CiteFactor, Canada/USA Vol. 18, No.2 2, April-June 2017 Palestrica of the third millennium ‒ Civilization and sport Vol. 18, no. 2, April-June 2017 Editorial Board Chief Editor Traian Bocu (Cluj-Napoca, Romania) Deputy Chief Editors Simona Tache (Cluj-Napoca, Romania) Ioan Onac (Cluj-Napoca, Romania) Dan Riga (Bucureşti, Romania) Adriana Filip (Cluj-Napoca, Romania) Bio-Medical, Health and Exercise Department Social sciences and Physical Activities Department Cezar Login (Cluj-Napoca, Romania) Dana Bădău (Tg. Mureş, Romania) Adriana Albu (Cluj-Napoca, Romania) Daniela Aducovschi (București, Romania) Adrian Aron (Radford, VA, USA) Dorin Almăşan (Cluj-Napoca,
    [Show full text]
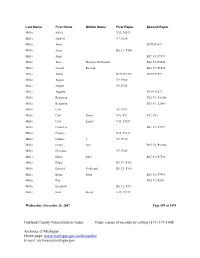
  • Oakland County Naturalization Index Order Copies of Records by Calling (517) 373-1408
    Last Name First Name Middle Name First Paper Second Paper Miller Alfred V23, P5293 Miller Andrew V7, P286 Miller Anna B17F2P3899 Miller Anna B6, F1, P144 Miller Anna B27, F4, P7874 Miller Anne Florence McDonald B20, F2, P5046 Miller Arnold Richard B24, F2, P6554 Miller Arthur B13F1P2571 B13F1P2572 Miller August V9, P300 Miller August V9, P353 Miller Augusta B14F1P2871 Miller Benjawan V35, F1, P12568 Miller Benjawan B35, F1, 12568 Miller Carl V9, P301 Miller Carl Ernest V32, P12 V32, P12 Miller Carl Ernest V15, P1187 Miller Carmelita B27, F1, P7597 Miller Charles V15, P1217 Miller Charles J V9, P330 Miller Chom Sun B35, F2, P12846 Miller Christian V9, P188 Miller Doris Ethel B27, F1, P7538 Miller Edgar B5, F1, P151 Miller Edward Ferdinand B5, F3, P114 Miller Elaine Mary B28, F1, P7984 Miller Elia B38, F1, P240 Miller Elizabeth B6, F2, P171 Miller Emil Henry V19, P3247 Wednesday, December 26, 2007 Page 899 of 1474 Oakland County Naturalization Index Order copies of records by calling (517) 373-1408 Archives of Michigan Home page: www.michigan.gov/archivesofmi E-mail: [email protected] Last Name First Name Middle Name First Paper Second Paper Miller Emily Caroline B8, F2, P104 Miller Ernest Lloyd B26, F1, P7107 Miller Eva Eleanore B23, F1, P6136 Miller Florence B9, F2, P9891 Miller Florence B28, F4, P8358 Miller Florence Theresa B9, F2, P9891 Miller Forest B17F4P4071 B17F4P4071 Miller Forest B6, F1, P268 Miller Frank Geoge V30, P24 V30, P24 Miller Frank George V12, P127 Miller Fred B18,F3,P4348 Miller Fred V9, P300 Miller Frederick George
    [Show full text]
  • Review of the Air Force Academy
    Review of the Air Force Academy The Scientific Informative Review, Vol. XV, No.3 (35)/2017 DOI: 10.19062/1842-9238.2017.15.3 BRAŞOV - ROMANIA SCIENTIFIC ADVISERS EDITORIAL BOARD Colonel Gabriel RĂDUCANU, PhD EDITOR-IN CHIEF (“Henri Coandă” Air Force Academy, Braşov, Romania) Col Prof Constantin-Iulian VIZITIU, PhD LtCol Assoc Prof Laurian GHERMAN, PhD (Military Technical Academy, Bucharest, Romania) (“Henri Coandă” Air Force Academy, Braşov, Romania) Prof Ion BĂLĂCEANU, PhD (Hyperion University, Bucharest, Romania) EDITORIAL ASSISTANTS Prof Necdet BILDIK, PhD (Celal Bayar University, Turkey) Prof Constantin ROTARU, PhD Assoc Prof Ella CIUPERCĂ, PhD (“Henri Coandă” Air Force Academy, Braşov, Romania) (National Intelligence Academy, Bucharest, Romania) Maj lect. Cosmina ROMAN, PhD Assoc Prof Nicoleta CORBU, PhD (“Henri Coandă” Air Force Academy, Braşov, Romania) (National School of Political Studies, Romania) Researcher Maria de Sao Jose CORTE-REAL, PhD EDITORS (Universidade Nova, Lisbon, Portugal) Researcher Alberto FORNASARI, PhD LtCol Assoc Prof Adrian LESENCIUC, PhD (“Aldo Moro” University of Bari, Bari, Italy) (“Henri Coandă” Air Force Academy, Braşov, Romania) Prof Vladimir HORAK, PhD Prof Traian ANASTASIEI, PhD (University of Defense, Brno, Czech Republic) (“Henri Coandă” Air Force Academy, Braşov, Romania) Assoc Prof Valentin ILIEV, PhD Assoc Prof Ludovic Dan LEMLE, PhD, (Technical University of Sofia, Bulgaria) (“Politehnica” University of Timisoara, Romania) Assoc Prof Berangere LARTIGUE, PhD Prof Eng. Jaroslaw KOZUBA, PhD (“Paul Sabatier” University, Toulouse, France) (Polish Air Force Academy, Deblin, Poland) Prof Marcela LUCA, PhD (Transilvania University, Braşov, Romania) Assist Prof Liliana MIRON, PhD Assoc Prof Doru LUCULESCU, PhD (“Henri Coandă” Air Force Academy, Braşov, Romania) (“Henri Coandă” Air Force Academy, Braşov, Romania) Lect.
    [Show full text]
  • 17Th International Multidisciplinary Scientific Geoconference (SGEM
    17th International Multidisciplinary Scientific GeoConference (SGEM 2017) Conference Proceedings Volume 17 Albena, Bulgaria 29 June - 5 July 2017 Issue 11, Part A ISBN: 978-1-5108-4819-1 1/29 Printed from e-media with permission by: Curran Associates, Inc. 57 Morehouse Lane Red Hook, NY 12571 Some format issues inherent in the e-media version may also appear in this print version. Copyright© (2017) by International Multidisciplinary Scientific GeoConferences (SGEM) All rights reserved. Printed by Curran Associates, Inc. (2017) For permission requests, please contact International Multidisciplinary Scientific GeoConferences (SGEM) at the address below. International Multidisciplinary Scientific GeoConferences (SGEM) 51 Alexander Malinov Blvd. fl 4, Office B5 1712 Sofia, Bulgaria Phone: +359 2 405 18 41 Fax: +359 2 405 18 65 [email protected] Additional copies of this publication are available from: Curran Associates, Inc. 57 Morehouse Lane Red Hook, NY 12571 USA Phone: 845-758-0400 Fax: 845-758-2633 Email: [email protected] Web: www.proceedings.com Contents CONFERENCE PROCEEDINGS CONTENTS SECTION GEOLOGY 1. A MULTISDICIPLINARY APPROACH TO CHARACTERIZE GRANITE BUILT HERITAGE IN NORTHWESTERN PORTUGAL, Angela Almeida and Fabiana Dias, Oporto University, Portugal ....................................................................... 3 2. ACCESSORY MINERALIZATION OF DOLOMITE RESERVOIRS AS THE FACTOR OF FLUIDS VARIABILITY COMPOSITION, Assoc. Prof. Dr. Eskin, Asscoc. Prof. Dr. Korolev, Assoc. Prof. Dr. Bakhtin, Assoc. Prof. Dr. Kolchugin, Assoc.
    [Show full text]
  • 2019 Year-End Prize Money Leaders
    2019 YEAR-END PRIZE MONEY LEADERS As of 25 November 2019 1 Rafael Nadal........................................$16,349,586 35 Nick Kyrgios ........................................$1,384,572 69 Marcel Granollers ...............................$870,663 2 Novak Djokovic....................................$13,372,355 36 Frances Tiafoe.....................................$1,375,737 70 Casper Ruud ........................................$848,872 3 Roger Federer ......................................$8,716,975 37 Marin Cilic ...........................................$1,359,590 71 Horacio Zeballos .................................$848,157 4 Dominic Thiem ....................................$8,000,223 38 Nicolas Mahut .....................................$1,355,053 72 Lorenzo Sonego ...................................$810,416 5 Daniil Medvedev ..................................$7,902,912 39 Fernando Verdasco .............................$1,293,590 73 Yoshihito Nishioka ..............................$810,305 6 Stefanos Tsitsipas ..............................$7,488,927 40 Milos Raonic........................................$1,291,082 74 Ugo Humbert .......................................$807,920 7 Alexander Zverev .................................$4,280,635 41 Feliciano Lopez ...................................$1,283,705 75 Andreas Seppi .....................................$807,276 8 Matteo Berrettini ................................$3,439,783 42 Taylor Fritz ..........................................$1,275,240 76 Nicolas Jarry .......................................$798,800
    [Show full text]
  • CAREER PRIZE MONEY LEADERS As Of: Oct 22, 2018
    CAREER PRIZE MONEY LEADERS As of: Oct 22, 2018 STANDING NAME NAT CAREER TOTAL 1 WILLIAMS, SERENA USA 88,233,301 2 WILLIAMS, VENUS USA 40,931,048 3 SHARAPOVA, MARIA RUS 38,342,119 4 WOZNIACKI, CAROLINE DEN 32,538,413 5 AZARENKA, VICTORIA BLR 29,278,989 6 RADWANSKA, AGNIESZKA POL 27,683,807 7 KVITOVA, PETRA CZE 27,191,207 8 HALEP, SIMONA ROU 27,095,579 9 KERBER, ANGELIQUE GER 26,852,841 10 HINGIS, MARTINA SUI 24,749,074 11 KUZNETSOVA, SVETLANA RUS 24,542,112 12 CLIJSTERS, KIM BEL 24,442,340 13 DAVENPORT, LINDSAY USA 22,166,338 14 GRAF, STEFFI GER 21,895,277 15 NAVRATILOVA, MARTINA USA 21,626,089 16 HENIN, JUSTINE BEL 20,863,335 17 JANKOVIC, JELENA SRB 19,089,259 18 STOSUR, SAMANTHA AUS 17,783,962 19 MUGURUZA, GARBIÑE ESP 17,377,384 20 SANCHEZ-VICARIO, ARANTXA ESP 16,942,640 21 LI, NA CHN 16,709,074 22 IVANOVIC, ANA SRB 15,510,787 23 MAURESMO, AMÉLIE FRA 15,022,476 24 SELES, MONICA USA 14,891,762 25 DEMENTIEVA, ELENA RUS 14,867,437 26 PENNETTA, FLAVIA ITA 14,197,886 27 ZVONAREVA, VERA RUS 13,883,142 28 CIBULKOVA, DOMINIKA SVK 13,459,963 29 PLISKOVA, KAROLINA CZE 13,427,441 30 ERRANI, SARA ITA 13,137,243 31 MAKAROVA, EKATERINA RUS 13,084,282 32 SAFAROVA, LUCIE CZE 12,624,268 33 VESNINA, ELENA RUS 12,527,014 34 PETROVA, NADIA RUS 12,466,924 35 STEPHENS, SLOANE USA 12,176,203 36 VINCI, ROBERTA ITA 11,808,215 37 MARTÍNEZ, CONCHITA ESP 11,527,977 38 SCHIAVONE, FRANCESCA ITA 11,324,245 39 NOVOTNA, JANA CZE 11,249,284 40 BARTOLI, MARION FRA 11,055,114 41 SUÁREZ NAVARRO, CARLA ESP 10,763,923 42 SAFINA, DINARA RUS 10,585,640 43 HANTUCHOVA, DANIELA
    [Show full text]