DOCSLIB.ORG

Van Der Waals Radii of Elements S

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Van Der Waals Radii of Elements S Inorganic Materials, Vol. 37, No. 9, 2001, pp. 871–885. Translated from Neorganicheskie Materialy, Vol. 37, No. 9, 2001, pp. 1031–1046. Original Russian Text Copyright © 2001 by Batsanov. Van der Waals Radii of Elements S. S. Batsanov Center for High Dynamic Pressures, Mendeleevo, Solnechnogorskii raion, Moscow oblast, 141570 Russia Received February 14, 2001 Abstract—The available data on the van der Waals radii of atoms in molecules and crystals are summarized. The nature of the continuous variation in interatomic distances from van der Waals to covalent values and the mechanisms of transformations between these types of chemical bonding are discussed. INTRODUCTION der Waals radius with the quantum-mechanical require- ment that the electron density vary continuously at the The notion that an interatomic distance can be periphery of atoms. thought of as the sum of atomic radii was among the most important generalizations in structural chemistry, In this review, the van der Waals radii of atoms eval- treating crystals and molecules as systems of interact- uated from XRD data, molar volumes, physical proper- ing atoms (Bragg, 1920). The next step forward in this ties, and crystal-chemical considerations are used to area was taken by Mack [1] and Magat [2], who intro- develop a universal system of van der Waals radii. duced the concept of nonvalent radius (R) for an atom situated at the periphery of a molecule and called it the atomic domain radius [1] or Wirkungsradius [2], ISOTROPIC CRYSTALLOGRAPHIC implying that this radius determines intermolecular dis- VAN DER WAALS RADII tances. Later, Pauling [3] proposed to call it the van der Kitaigorodskii [4, 5] was the first to formulate the Waals radius, because it characterizes van der Waals principle of close packing of molecules in crystalline interactions between atoms. He also showed that the phases. He assumed that the van der Waals areas of van der Waals radii of nonmetals coincide with their peripheral atoms in neighboring molecules are in con- ionic radii and exceed their covalent radii (r), typically tact but do not overlap (rigid-atom model), because the by 0.8 Å. repulsive forces between closed electron shells rise Initially, only x-ray diffraction (XRD) data, molar sharply with decreasing intermolecular distance. He volume measurements, and crystal-chemical consider- made up a system of van der Waals radii as consistent ations were used to determine R. Later studies extended as possible with the intermolecular distances in organic the range of experimental approaches and culminated compounds. His radii differed little from Pauling’s in a complete system of the van der Waals radii of free (Table 1). and bound atoms. Comparison of the results obtained The system of van der Waals radii was further by various physical methods made it possible to assess refined by Bondi [6, 7]. His detailed tables were very the accuracy and locate the applicability limits of the popular among chemists, even though the values of R van der Waals radii and to reconcile the concept of van were criticized in a number of works [8]. Bondi not Table 1. Crystallographic van der Waals radii of nonmetals R, Å Author, year HFClBrIOSNC Pauling, 1939 1.2 1.35 1.80 1.95 2.15 1.40 1.85 1.5 1.70 Bondi, 1964 1.20 1.47 1.75 1.85 1.98 1.52 1.80 1.55 1.70 Zefirov, 1974 1.16 1.40 1.90 1.97 2.14 1.29 1.84 1.50 1.71 Gavezzotti, 1983–1999 1.17 1.35 1.80 1.95 2.10 1.40 1.85 1.50 1.70 Batsanov, 1995 1.80 1.90 2.10 1.51 1.80 1.68 Wieberg, 1995 1.5 1.8 1.9 2.1 1.5 1.8 1.6 1.7 Rowland, 1996 1.10 1.46 1.76 1.87 2.03 1.58 1.81 1.64 1.77 0020-1685/01/3709-0871 $25.00 © 2001 MAIK “Nauka/Interperiodica” 872 BATSANOV R RM RX AA M X r rX dMX Fig. 1. Schematic showing the formation of an A2 molecule. Fig. 2. Schematic showing the formation of an M–X bond. only determined R from structural data but also calcu- molecular compounds [20, 21]. Let us outline these lated R by adding 0.76 Å to covalent radii and evaluated approaches and the obtained results. R from thermodynamic and physical properties. The R Since the valence state of a metal remains values recommended by Bondi are also listed in unchanged upon a polymorphic transformation, while Table 1. the bond number increases, the electron density redis- Zefirov and Zorkii [9, 10] corrected some of the van tributes between ligands, der Waals radii and made a number of new suggestions, ∆V ==2∆V 3∆V …, (1) in particular, that R should be calculated from the short- 1 2 3 est intermolecular distances (D), ensuring a three- where ∆V is the volume common to the two atomic dimensional system of contacts, since other peripheral spheres (Fig. 1), and the subscripts specify the bond atoms of the molecule may be not in contact, and the number. It is easily seen that determination of R by averaging all intermolecular dis- 2 2 tances may be unjustified. Although they highlight the ∆V = ---π()Rr– ()2Rr+ . (2) statistical nature of van der Waals radii and their vari- 3 ability within a few tenths of an ångström, depending Given that, in polymorphic transformations, a decrease on various structural factors, the radii in their system in the intermolecular contact area is accompanied by an are given with an accuracy of a few thousandths of an increase in covalent bond length [22], to each coordina- ångström (Table 1). tion number Nc there correspond particular R and r. A classical approach to the determination of the van Therefore, Eq. (1) takes the form der Waals radii of organogens was proposed in [11–14] ()2()()2()… (Table 1). The system of van der Waals radii of nonmet- R1 – r1 2R1 + r1 ==2 R2 – r2 R2 + r2 , (3) als elaborated by Rowland and Taylor [15] for struc- valid for univalent atoms. In the case of multivalent tural organic chemistry was based on a wealth of statis- metals, the left-hand side of Eq. (3) should be multi- tical data. plied by valence v if single-bond radii are used as r [3]. The van der Waals radii of the halogens and carbon As a result, we obtain in inorganic compounds were first determined by Paul- ()2()()2() ing [3], who used data on layered compounds such as R1 – r1 R1 + r1 = nRn – rn Rn + rn , (4) CdCl2 and graphite. Later, the van der Waals radii of where n = Nc/v. Taking into account that the maximal halogens and chalcogens were evaluated from a large N in metals is 12, one can use Eq. (4) to calculate R body of experimental data [16]: OH 1.51, Cl 1.80, c Br 1.90, I 2.10, S 1.80, Se 1.85, and Te 2.02 Å. corresponding to the largest change in Nc upon the polymorphic transformation. Such calculations were The van der Waals radii of metals are difficult to carried out [17] under the assumption that, upon an determine directly, because there is only a small num- increase in Nc, the decrease in R is proportional to the ber of structures in which metal atoms can be in contact increase in r (Table 2). with another molecule; with the development of struc- In another approach to determining R, the M–X tural chemistry, the number of such structures bond is also thought of as the region common to the increases. Table 2 lists the crystallographic van der atomic spheres M and X, with an internuclear distance Waals radii determined to date [16–19]. dMX (Fig. 2). It is easily seen that Recently, the van der Waals radii of metals were cal- ()2 2 1/2 culated from structural data for metals [17] and their RM = RX + dMX – 2dMXrM . (5) INORGANIC MATERIALS Vol. 37 No. 9 2001 VAN DER WAALS RADII OF ELEMENTS 873 Table 2. Crystallographic van der Waals radii of metals R, Å Atom [17] [20] [21] empirical [25] (9) Li 2.24 2.25 2.24 2.05 2.1 Na 2.57 2.40 2.39 2.3 K 3.00 2.67 2.67 2.7 Rb 3.12 2.78 2.76 2.8 Cs 3.31 2.90 2.93 2.9 3.1 2.9 Cu 2.00 2.16 2.14 2.09 1.9 1.9 Ag 2.13 2.25 2.29 1.9 2.0 Au 2.13 2.18 2.0 Be 1.86 2.03 1.99 1.86 1.8 Mg 2.27 2.22 2.25 2.10 2.2 Ca 2.61 2.43 2.27 2.17 2.6 Sr 2.78 2.54 2.40 2.36 2.7 Ba 2.85 2.67 2.55 2.52 2.8 Zn 2.02 2.09 2.16 2.12 2.1 2.0 Cd 2.17 2.18 2.29 2.1 Hg 2.17 2.15 2.28 1.75 [18] 1.95 2.1 Sc 2.28 2.37 2.18 2.3 2.25–2.41 Y 2.45 2.47 2.38 1.8 2.4 2.33–2.46 La 2.51 2.58 2.59 2.6 2.30–2.44 B 1.74 1.87 1.72 1.7 1.83 1.75 1.91–2.00 Al 2.11 2.19 2.17 1.97 2.02 2.0 2.29–2.38 Ga 2.08 2.17 2.16 2.14 2.05 2.0 1.95–2.02 In 2.24 2.28 2.29 2.32 2.2 2.09–2.15 Tl 2.25 2.29 2.42 2.05 1.92 2.3 2.01–2.07 Ti 2.14 2.30 2.22 2.0 2.1 2.11–2.19 Zr 2.25 2.38 2.31 2.3 2.2 2.20–2.29 Hf 2.24 2.34 2.29 2.3 2.04–2.12 Si 2.06 2.06 2.19 2.15 1.95 2.10–2.22 Ge 2.13 2.10 2.22 2.0 2.0 1.91–2.02 Sn 2.29 2.21 2.29 2.40 2.2 2.2 2.02–2.10 Pb 2.36 2.24 2.46 2.3 2.3 2.00–2.08 V 2.03 2.14 2.0 2.0 2.05–2.19 Nb 2.13 2.34 2.15 2.1 1.96–2.10 Ta 2.13 2.26 2.22 2.2 1.93–2.05 As 2.16 2.05 2.14 1.96 2.0 1.92 Sb 2.33 2.20 2.32 2.2 2.06–2.10 Bi 2.42 2.28 2.40 2.22 2.40 [19] 2.4 2.04–2.08 Cr 1.97 2.27 2.05 2.0 2.0 2.06–2.20 Mo 2.06 2.29 2.16 2.2 2.1 1.92–2.00 W 2.07 2.23 2.14 2.2 2.1 1.85–1.93 Mn 1.96 2.15 2.23 [24] 2.00 2.0 2.00–2.14 Tc 2.04 2.11 2.1 1.93–2.02 Re 2.05 2.21 2.11 2.1 1.78–1.86 Fe 1.96 2.19 1.98 2.1 2.0 2.05–2.25 Co 1.95 2.16 1.97 2.0 1.94–2.14 Ni 1.94 2.14 1.97 2.0 1.88–2.11 Ru 2.02 2.05 2.16 2.1 1.89–1.97 Rh 2.02 2.04 2.1 1.83–1.90 Pd 2.05 2.14 2.1 1.87–1.96 Os 2.03 2.02 2.1 1.76–1.82 Ir 2.03 2.01 2.1 1.76–1.82 Pt 2.06 2.15 2.1 2.02 2.1 1.77–1.85 Th 2.43 2.54 2.50 2.25 U 2.17 2.51 2.45 1.94 * Minimal radius from M···H van der Waals distances for R(H) = 1.2 Å [32].
Load more

Recommended publications
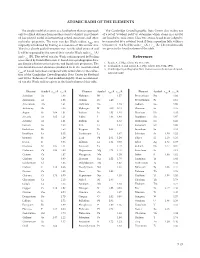
  • ATOMIC RADII of the ELEMENTS References
    ATOMIC RADII OF THE ElEMENTS The simple model of an atom as a hard sphere that can approach The Cambridge Crystallographic Data Center also makes use only to a fixed distance from another atom to which it is not bond- of a set of “covalent radii” to determine which atoms in a crystal ed has proved useful in interpreting crystal structures and other are bonded to each other . Thus two atoms A and B are judged to molecular properties . The term van der Waals radius, rvdw, was be connected by a covalent bond if their separation falls within a originally introduced by Pauling as a measure of this atomic size . tolerance of ±0 .4 Å of the sum rcov (A) + rcov (B) . The covalent radii Thus in a closely packed structure two non-bonded atoms A and are given in the fourth column of the table . B will be separated by the sum of their van der Waals radii rvdw (A) and rvdw (B) . The set of van der Waals radii proposed by Pauling References was refined by Bondi (Reference 1) based on crystallographic data, gas kinetic collision cross sections, and liquid state properties . The 1 . Bondi, A ., J. Phys. Chem. 68, 441, 1964 . non-bonded contact distances predicted from the recommended 2 . Rowland, R . S . and Taylor, R ., J. Phys. Chem. 100, 7384, 1996 . 3 . Cambridge Crystallographic Data Center, www .ccdc .cam .ac .uk/prod- r of Bondi have been compared with actual data in the collec- vdw ucts/csd/radii/ tion of the Cambridge Crystallographic Data Center by Rowland and Taylor (Reference 2) and modified slightly .
    [Show full text]
  • Atomic and Ionic Radii of Elements 1–96 Martinrahm,*[A] Roald Hoffmann,*[A] and N
    DOI:10.1002/chem.201602949 Full Paper & Elemental Radii Atomic and Ionic Radii of Elements 1–96 MartinRahm,*[a] Roald Hoffmann,*[a] and N. W. Ashcroft[b] Abstract: Atomic and cationic radii have been calculated for tive measureofthe sizes of non-interacting atoms, common- the first 96 elements, together with selected anionicradii. ly invoked in the rationalization of chemicalbonding, struc- The metric adopted is the average distance from the nucleus ture, and different properties. Remarkably,the atomic radii where the electron density falls to 0.001 electrons per bohr3, as defined in this way correlate well with van der Waals radii following earlier work by Boyd. Our radii are derived using derived from crystal structures. Arationalizationfor trends relativistic all-electron density functional theory calculations, and exceptionsinthose correlations is provided. close to the basis set limit. They offer asystematic quantita- Introduction cule,[2] but we prefer to follow through with aconsistent pic- ture, one of gauging the density in the atomic groundstate. What is the size of an atom or an ion?This question has been The attractivenessofdefining radii from the electron density anatural one to ask over the centurythat we have had good is that a) the electron density is, at least in principle, an experi- experimental metricinformation on atoms in every form of mental observable,and b) it is the electron density at the out- matter,and (more recently) reliable theory for thesesame ermost regionsofasystem that determines Pauli/exchange/ atoms. And the momentone asks this question one knows same-spinrepulsions, or attractive bondinginteractions, with that there is no unique answer.Anatom or ion coursing down achemical surrounding.
    [Show full text]
  • ARC: an Open-Source Library for Calculating Properties of Alkali Rydberg Atoms
    ARC: An open-source library for calculating properties of alkali Rydberg atoms N. Šibalic´a,∗, J. D. Pritchardb, C. S. Adamsa, K. J. Weatherilla aJoint Quantum Center (JQC) Durham-Newcastle, Department of Physics, Durham University, South Road, Durham, DH1 3LE, United Kingdom bDepartment of Physics, SUPA, University of Strathclyde, 107 Rottenrow East, Glasgow, G4 0NG, United Kingdom Abstract We present an object-oriented Python library for computation of properties of highly-excited Rydberg states of alkali atoms. These include single-body effects such as dipole matrix elements, excited-state lifetimes (radiative and black-body limited) and Stark maps of atoms in external electric fields, as well as two-atom interaction potentials accounting for dipole and quadrupole coupling effects valid at both long and short range for arbitrary placement of the atomic dipoles. The package is cross-referenced to precise measurements of atomic energy levels and features extensive documentation to facilitate rapid upgrade or expansion by users. This library has direct application in the field of quantum information and quantum optics which exploit the strong Rydberg dipolar interactions for two-qubit gates, robust atom-light interfaces and simulating quantum many-body physics, as well as the field of metrology using Rydberg atoms as precise microwave electrometers. Keywords: Alkali atom, Matrix elements, Dipole-dipole interactions, Stark shift, Förster resonances PROGRAM SUMMARY They are a flourishing field for quantum information process- Program Title: ARC: Alkali Rydberg Calculator ing [1, 2] and quantum optics [3, 4, 5] in the few to single exci- Licensing provisions: BSD-3-Clause tation regime, as well as many-body physics [6, 7, 8, 9, 10, 11], Programming language: Python 2.7 or 3.5, with C extension in the many-excitations limit.
    [Show full text]
  • Chalcogen-Nitrogen Bond: Insights Into a Key Chemical Motif
    Proceedings Chalcogen-nitrogen Bond: Insights into A Key Chemical Motif Marco Bortoli,1 Andrea Madabeni,1 Pablo Andrei Nogara,2 Folorunsho B. Omage,2 Giovanni Ribaudo,3 Davide Zeppilli,1 Joao Batista Teixeira Rocha,2* Laura Orian1* 1 Dipartimento di Scienze Chimiche Università degli Studi di Padova Via Marzolo 1 35131 Padova, Italy; [email protected] (M.B.); [email protected] (A.M..); [email protected] (D.Z.) 2 Departamento de Bioquímica e Biologia Molecular, Universidade Federal de Santa Maria, Santa Maria, 97105-900, RS Brazil; [email protected] (P.A.N.); [email protected] (F.B.O.) 3 Dipartimento di Medicina Molecolare e Traslazionale, Università degli Studi di Brescia, Viale Europa 11, 25123 Brescia, Italy; [email protected] (G.R.) * Correspondence: : [email protected] (J.B.T.R), [email protected] (L.O.); † Presented at the 1st International Electronic Conference on Catalysis Sciences, 10–30 November 2020; Available online: https://eccs2020.sciforum.net/ Published: 10 November 2020 Abstract: Chalcogen-nitrogen chemistry deals with systems in which sulfur, selenium or tellurium is linked to a nitrogen nucleus. This chemical motif is a key component of different functional structures, ranging from inorganic materials and polymers to rationally designed catalysts, to bioinspired molecules and enzymes. The formation of a selenium-nitrogen bond, and its disruption, are rather common events in organic Se-catalyzed processes. In nature, along the mechanistic path of glutathione peroxidase, evidence of the formation of a Se-N bond in highly oxidizing conditions has been reported and interpreted as a strategy to protect the selenoenzyme from overoxidation.
    [Show full text]
  • Quantum-Mechanical Relation Between Atomic Dipole Polarizability and the Van Der Waals Radius (Supplemental Material)
    Quantum-Mechanical Relation between Atomic Dipole Polarizability and the van der Waals Radius Dmitry V. Fedorov,1, ∗ Mainak Sadhukhan,1 Martin St¨ohr,1 and Alexandre Tkatchenko1 1Physics and Materials Science Research Unit, University of Luxembourg, L-1511 Luxembourg The atomic dipole polarizability, α, and the van der Waals (vdW) radius, RvdW, are two key quantities to describe vdW interactions between atoms in molecules and materials. Until now, they have been determined independently and separately from each other. Here, we derive the quantum- 1/7 mechanical relation RvdW = const. × α which is markedly different from the common assumption 1/3 RvdW ∝ α based on a classical picture of hard-sphere atoms. As shown for 72 chemical elements between hydrogen and uranium, the obtained formula can be used as a unified definition of the vdW radius solely in terms of the atomic polarizability. For vdW-bonded heteronuclear dimers consisting of atoms A and B, the combination rule α = (αA + αB )/2 provides a remarkably accurate way to calculate their equilibrium interatomic distance. The revealed scaling law allows to reduce the empiricism and improve the accuracy of interatomic vdW potentials, at the same time suggesting the existence of a non-trivial relation between length and volume in quantum systems. The idea to use a specific radius, describing a distance by Bondi [8] has been extensively used. However, it is an atom maintains from other atoms in non-covalent in- based on a restricted amount of experimental informa- teractions, was introduced by Mack [1] and Magat [2]. tion available at that time. With the improvement of Subsequently, it was employed by Kitaigorodskii in his experimental techniques and increase of available data, theory of close packing of molecules in crystals [3, 4].
    [Show full text]
  • Recent Developments in Chalcogen Chemistry
    RECENT DEVELOPMENTS IN CHALCOGEN CHEMISTRY Tristram Chivers Department of Chemistry, University of Calgary, Calgary, Alberta, Canada WHERE IS CALGARY? Lecture 1: Background / Introduction Outline • Chalcogens (O, S, Se, Te, Po) • Elemental Forms: Allotropes • Uses • Trends in Atomic Properties • Spin-active Nuclei; NMR Spectra • Halides as Reagents • Cation Formation and Stabilisation • Anions: Structures • Solutions of Chalcogens in Ionic Liquids • Oxides and Imides: Multiple Bonding 3 Elemental Forms: Sulfur Allotropes Sulfur S6 S7 S8 S10 S12 S20 4 Elemental Forms: Selenium and Tellurium Allotropes Selenium • Grey form - thermodynamically stable: helical structure cf. plastic sulfur. R. Keller, et al., Phys. Rev. B. 1977, 4404. • Red form - cyclic Cyclo-Se8 (cyclo-Se7 and -Se6 also known). Tellurium • Silvery-white, metallic lustre; helical structure, cf. grey Se. • Cyclic allotropes only known entrapped in solid-state structures e.g. Ru(Ten)Cl3 (n = 6, 8, 9) M. Ruck, Chem. Eur. J. 2011, 17, 6382 5 Uses – Sulfur Sulfur : Occurs naturally in underground deposits. • Recovered by Frasch process (superheated water). • H2S in sour gas (> 70%): Recovered by Klaus process: Klaus Process: 2 H S + SO 3/8 S + 2 H O 2 2 8 2 • Primary industrial use (70 %): H2SO4 in phosphate fertilizers 6 Uses – Selenium and Tellurium Selenium and Tellurium : Recovered during the refining of copper sulfide ores Selenium: • Photoreceptive properties – used in photocopiers (As2Se3) • Imparts red color in glasses Tellurium: • As an alloy with Cu, Fe, Pb and to harden
    [Show full text]
  • Monte Carlo Simulations of Polonium Drift from Radon Progeny in an Electrostatic Counter
    Monte Carlo Simulations of Polonium Drift from Radon Progeny in an Electrostatic Counter Devon Seymour Advised by Richard Gaitskell Brown University, Dept. of Physics, Providence RI 02912, USA May 4, 2017 1 Physics Motivation During the past two decades, a standard cosmological picture of the universe (the Lambda Cold Dark Matter or LCDM model) has emerged, which includes a detailed breakdown of the main constituents of the energy density of the universe. This theoretical framework is now on a firm empirical footing, given the remarkable agreement of a diverse set of astrophysical data. Recent results by Planck largely confirm the earlier Wilkinson Microwave Anisotropy Probe (WMAP) conclusions and confirm that the universe is spatially flat, with an acceleration in the rate of expansion and an energy budget comprising approximately 5% baryonic matter, 26% cold dark matter (CDM), and 69% dark energy[1]. Astrophysical measurements on mul- tiple length scales show that dark matter is consistent with like a particle model and not a modification of gravity. Grav- itational lensing of distant galaxies by foreground galactic clusters can provide a map of the total gravitational mass, showing that this mass far exceeds that Figure 1: LZ sensitivity projections. The of ordinary baryonic matter. baseline LZ assumptions give the solid black curve. LUX and ZEPLIN results The LUX-ZEPLIN (LZ) experiment are shown in broken blue lines. If LZ achieves its design goals (e.g., reducing the will attempt to establish the existence of radon background), the sensitivity would a type of dark matter known as WIMPs improve, resulting in the magenta sensi- tivity curve.
    [Show full text]
  • Python Module Index 79
    mendeleev Documentation Release 0.9.0 Lukasz Mentel Sep 04, 2021 CONTENTS 1 Getting started 3 1.1 Overview.................................................3 1.2 Contributing...............................................3 1.3 Citing...................................................3 1.4 Related projects.............................................4 1.5 Funding..................................................4 2 Installation 5 3 Tutorials 7 3.1 Quick start................................................7 3.2 Bulk data access............................................. 14 3.3 Electronic configuration......................................... 21 3.4 Ions.................................................... 23 3.5 Visualizing custom periodic tables.................................... 25 3.6 Advanced visulization tutorial...................................... 27 3.7 Jupyter notebooks............................................ 30 4 Data 31 4.1 Elements................................................. 31 4.2 Isotopes.................................................. 35 5 Electronegativities 37 5.1 Allen................................................... 37 5.2 Allred and Rochow............................................ 38 5.3 Cottrell and Sutton............................................ 38 5.4 Ghosh................................................... 38 5.5 Gordy................................................... 39 5.6 Li and Xue................................................ 39 5.7 Martynov and Batsanov........................................
    [Show full text]
  • Thorium Periodic Table of Elements
    Periodic Table of Elements https://periodic-table.pro/Element/Th/enView online at https://periodic-table.pro Thorium This foil is what remains after useful shapes were stamped out, but what those shapes were useful for remains a mystery. Pure thorium metal like this is quite rare, and not easily obtained. 01. OVERVIEW Symbol Th Atomic number 90 Atomic weight 232.0381 Density 11.724 g/cm³ Melting point 1750 °C Boiling point 4820 °C 02. THERMAL PROPERTIES Phase Solid Melting point 1750 °C Boiling point 4820 °C Absolute melting point 2023 K Absolute boiling point 5093 K Critical pressure N/A Critical temperature N/A Heat of fusion 16 kJ/mol Heat of vaporization 530 kJ/mol Heat of combustion N/A Specific heat 118 J/(kg K) Adiabatic index N/A Neel point N/A Thermal conductivity 54 W/(m K) Thermal expansion 0.000011 K¹ 03. PHYSICAL PROPERTIES Density 11.724 g/cm³ Density (liquid) N/A Molar volume 0.0000197917 Molar mass 232.03806 u Brinell hardness 400 MPa Mohs hardness 3 MPa Vickers hardness 350 MPa Bulk modulus 54 GPa Shear modulus 31 GPa Young modulus 79 GPa Poisson ratio 0.27 Refractive index N/A Speed of sound 2490 m/s Thermal conductivity 54 W/(m K) Thermal expansion 0.000011 K¹ 04. REACTIVITY Valence 4 Electronegativity 1.3 Electron affinity N/A Ionization energies 587, 1110, 1930, 2780 kJ/mol 05. SAFETY Autoignition point 130 °C Flashpoint N/A Heat of combustion N/A 06. CLASSIFICATIONS Alternate names N/A Names of allotropes N/A Block, Group, Period f, N/A, 7 Electron configuration [Rn]6d²7s² Color Silver Discovery 1829 in Sweden Gas phase N/A 07.
    [Show full text]
  • Does Oxygen Feature Chalcogen Bonding?
    molecules Article Does Oxygen Feature Chalcogen Bonding? Pradeep R. Varadwaj 1,2 1 Department of Chemical System Engineering, School of Engineering, The University of Tokyo 7-3-1, Tokyo 113-8656, Japan; [email protected] or [email protected] 2 The National Institute of Advanced Industrial Science and Technology (AIST), Tsukuba 305-8560, Japan Received: 20 July 2019; Accepted: 28 August 2019; Published: 30 August 2019 Abstract: Using the second-order Møller–Plesset perturbation theory (MP2), together with Dunning’s all-electron correlation consistent basis set aug-cc-pVTZ, we show that the covalently bound oxygen atom present in a series of 21 prototypical monomer molecules examined does conceive a positive (or a negative) σ-hole. A σ-hole, in general, is an electron density-deficient region on a bound atom M along the outer extension of the R–M covalent bond, where R is the reminder part of the molecule, and M is the main group atom covalently bonded to R. We have also examined some exemplar 1:1 binary complexes that are formed between five randomly chosen monomers of the above series and the nitrogen- and oxygen-containing Lewis bases in N2, PN, NH3, and OH2. We show that the O-centered positive σ-hole in the selected monomers has the ability to form the chalcogen bonding interaction, and this is when the σ-hole on O is placed in the close proximity of the negative site in the partner molecule. Although the interaction energy and the various other 12 characteristics revealed from this study indicate the presence of any weakly bound interaction between the monomers in the six complexes, our result is strongly inconsistent with the general view that oxygen does not form a chalcogen-bonded interaction.
    [Show full text]
  • Theoretical Study of Xenon Adsorption in Uo2nanoporous Matrices Mehdi Colbert, Guy Treglia, Fabienne Ribeiro
    Theoretical study of xenon adsorption in UO2nanoporous matrices Mehdi Colbert, Guy Treglia, Fabienne Ribeiro To cite this version: Mehdi Colbert, Guy Treglia, Fabienne Ribeiro. Theoretical study of xenon adsorption in UO2nanoporous matrices. Journal of Physics: Condensed Matter, IOP Publishing, 2014, 26, 10.1088/0953-8984/26/48/485015. hal-03040139 HAL Id: hal-03040139 https://hal.archives-ouvertes.fr/hal-03040139 Submitted on 4 Dec 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Home Search Collections Journals About Contact us My IOPscience Theoretical study of xenon adsorption in UO2 nanoporous matrices This content has been downloaded from IOPscience. Please scroll down to see the full text. 2014 J. Phys.: Condens. Matter 26 485015 (http://iopscience.iop.org/0953-8984/26/48/485015) View the table of contents for this issue, or go to the journal homepage for more Download details: IP Address: 139.124.20.101 This content was downloaded on 27/11/2014 at 12:59 Please note that terms and conditions apply. Journal of Physics: Condensed Matter
    [Show full text]
  • Quantitative Assessment of the Atom Radii of Chemical Elements Based on Spectral Analysis Data
    Advances in Engineering Research, volume 177 International Symposium on Engineering and Earth Sciences (ISEES 2018) Quantitative Assessment of the Atom Radii of Chemical Elements Based on Spectral Analysis Data B. L. Aleksandrov E. A. Aleksandrova Department of Physics Department of Chemistry Kuban State Agrarian University Kuban State Agrarian University Krasnodar, Russia Krasnodar, Russia [email protected] [email protected] L. Sh. Makhmudova Zh. T. Khadisova Chemical Technology of Oil and Gas Department Chemical Technology of Oil and Gas Department M.D. Millionshtchikov Grozny State Oil Technical M.D. Millionshtchikov Grozny State Oil Technical University University Grozny, Russia Grozny, Russia [email protected] [email protected] Abstract— Atom radii are calculated for chemical elements in different energy states based on photon energy of the emission (absorption) spectrum of atoms. II. DIFFERENT CONCEPTS OF AN ATOMIC RADIUS To define a radius of the atom, a number of concepts are Keywords: atom, radius, emission spectrum, photon applicable depending on the modeling paradigm, classical or I. INTRODUCTION quantum mechanical one: atomic, orbital, effective, covalent, or van der Waals radius. In the N. Bohr model of the atom, The term nanotechnology stands for a set of methods and where electrons travel in defined circular orbits (i.e. energy techniques used to create materials with dimensions in the levels), the radius of the atom is the distance from the center nanometre scale (at atomic and molecular levels) in order to of the nucleus to the furthest electron orbit. An atomic radius produce new products with predetermined properties. Other is a characteristic of an atom that allows for an approximate well-known concepts include molecular nanotechnology estimation of interatomic (inter-nuclear) distances in (MNT) by K.
    [Show full text]