DOCSLIB.ORG

Modelling of Microgrid Energy Systems with Concentrated Solar Power

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Modelling of Microgrid Energy Systems with Concentrated Solar Power Modelling of microgrid energy systems with concentrated solar power Niccolò Oggioni Master of Science Thesis KTH School of Industrial Engineering and Management Energy Technology EGI-2019-MJ232X Division of Heat and Power Technology SE-100 44 STOCKHOLM Ai miei genitori, per il loro costante e indiscusso supporto, A mio fratello Jacopo, per essersi preso cura di mamma e papà in questi due anni, A te, Elena, per esserci sempre stata. Master of Science Thesis EGI 2019: MJ232X Modelling of microgrid energy systems with concentrated solar power Niccolò Oggioni Approved Examiner Supervisor 31/07/19 Björn Laumert Rafael E. Guédez Mata Commissioner Contact person Azelio Martin Nilsson Abstract This master’s thesis presents the work performed during a four-month long internship at Azelio AB in Gothenburg. Energy performance models for common energy technologies in microgrid energy systems were developed and validated. The investigated technologies are traditional and bifacial PV modules, wind turbines, Li-ion battery energy storage systems and diesel generators. Subsequently, they were utilised to simulate the energy supply of two remote communities in Queensland, Australia. Azelio’s CSP technology, which combines heliostats, thermal energy storage with phase change materials and Stirling engine, was introduced as well. By means of scenarios and key performance indicators, the possibility of disconnecting such towns from the local electricity distribution network was investigated. Both technical and economic aspects were analysed. This led to the conclusion that 10 MW CSP system would be sufficient to achieve grid independence if extra backup capacity, e.g. diesel generators, or demand- side control strategies, are introduced. Sensitivity analysis performed on the possibility of dividing the CSP park into two clusters, the smaller one being subject to a power threshold, was investigated as well. In terms of economic feasibility, off-grid systems resulted more expensive than maintaining the grid connection. Sammanfattning Denna master’s uppsats presenterar alla resultat från examensarbetet hos Azelio AB i Göteborg. Energy performance models för de vanligaste energiteknologerna i microgrid energisystemen designades och validerades. De forskade energiteknologerna var traditionella och bifacial solpaneler, vindkraft, energilagring genom Li- ion batterier och dieselgeneratorer. Modellerna användes för att simulera energiförsörjning av olika energisystem som representerar två isolerade byar i Queensland, Australia. Azelio’s CSP teknologi, som består av heliostater, värmenergilagring med phase change material och en Stirlingmotor, introducerades också. Genom att designa olika scenarier och key perfomance indicators, möjligheten att koppla av byarna ifrån det lokala kraftnätsystemet utforskades. Båda tekniska och ekonomiska synpunkter värderades. Det beslutades att 10 MW CSP kapacitet kan vara nog i mycket för att nå energisjälvständighet om ytterligare backupkapacitet, t.ex. en dieselgenerator, eller demand side control strategies introducerades. Känslighetsanalys utforskade möjligheten att dela CSP systemet i två olika delar, där den med lägre kapacitet kunde avkopplas för att undvika onödig energiförsörjning. Om ekonomiska utförbarhet, off-grid system verkade dyrare än sådana system där byarna var fortfarande kopplat till det lokala kraftnätet. Acknowledgements I would like to thank my KTH supervisor, Rafael Guédez, for his support and helpful insights, and, most importantly, for having given me the chance to collaborate with him and Azelio AB. Special thanks to my supervisor at Azelio AB, Martin Nilsson. Without him I would have never been able to complete this project. His help and feedbacks have always been treasured, especially his patience in introducing me to Modelica. I would also like to thank the entire Azelio team at the Gothenburg office, for the warm welcome and inclusion, for all the shared lunchbreaks and laughs. ii Table of Contents List of figures ................................................................................................................................................................ iv List of tables ................................................................................................................................................................. vii Abbreviations and nomenclature ............................................................................................................................... ix 1 Introduction .......................................................................................................................................................... 1 1.1 Objective and methodology ...................................................................................................................... 3 2 Literature review ................................................................................................................................................... 4 2.1 Modelling language and software ............................................................................................................. 4 2.2 Azelio’s CSP technology ............................................................................................................................ 4 2.2.1 Stirling engine ..................................................................................................................................... 4 2.2.2 Phase Change Materials and Thermal Energy Storage ................................................................ 5 2.3 Solar PV modules and bifacial PV modules ........................................................................................... 6 2.4 Wind turbines .............................................................................................................................................. 8 2.5 Diesel generators ......................................................................................................................................... 9 2.6 Battery storage ............................................................................................................................................. 9 2.7 Microgrids ..................................................................................................................................................11 3 System modelling ................................................................................................................................................12 3.1 Azelio AB’s CSP with integrated TES ...................................................................................................12 3.2 Solar PV and bifacial PV modules .........................................................................................................14 3.2.1 PV modules and arrays....................................................................................................................14 3.2.2 Bifacial PV modules and arrays .....................................................................................................16 3.2.3 Inverter ..............................................................................................................................................18 3.3 Wind turbines and wind farm .................................................................................................................19 3.3.1 Wind shear ........................................................................................................................................19 3.3.2 Wind turbine .....................................................................................................................................20 3.3.3 Wind farm .........................................................................................................................................25 3.4 Diesel generators .......................................................................................................................................27 3.4.1 Estimated fuel consumption ..........................................................................................................27 3.4.2 Manufacturer fuel consumption ....................................................................................................28 3.5 Battery storage ...........................................................................................................................................29 3.5.1 Power model .....................................................................................................................................29 3.5.2 Thermal model .................................................................................................................................30 3.6 Grid connection ........................................................................................................................................32 3.7 Examples of integrated model ................................................................................................................32 3.7.1 Energy system without CSP ...........................................................................................................32 3.7.2 CSP integrated energy system ........................................................................................................33 4 Case study: remote communities in Queensland, Australia ........................................................................34 iii 4.1 Introduction ...............................................................................................................................................34
Load more

Recommended publications
  • Renewable Energy Across Queensland's Regions
    Renewable Energy across Queensland’s Regions July 2018 Enlightening environmental markets Green Energy Markets Pty Ltd ABN 92 127 062 864 2 Domville Avenue Hawthorn VIC 3122 Australia T +61 3 9805 0777 F +61 3 9815 1066 [email protected] greenmarkets.com.au Part of the Green Energy Group Green Energy Markets 1 Contents 1 Introduction ........................................................................................................................6 2 Overview of Renewable Energy across Queensland .....................................................8 2.1 Large-scale projects ..................................................................................................................... 9 2.2 Rooftop solar photovoltaics ........................................................................................................ 13 2.3 Batteries-Energy Storage ........................................................................................................... 16 2.4 The renewable energy resource ................................................................................................. 18 2.5 Transmission .............................................................................................................................. 26 3 The renewable energy supply chain ............................................................................. 31 3.1 Construction activity .................................................................................................................... 31 3.2 Equipment manufacture
    [Show full text]
  • Department of Energy and Water Supply CS2731 09/13 ISSN 2201-2095
    Department of Energy and Water Supply CS2731 09/13 ISSN 2201-2095 Interpreter statement The Queensland Government is committed to providing accessible services to Queenslanders from all culturally and linguistically diverse backgrounds. If you have difficulty in understanding the annual report, you can contact us on 13 QGOV and we will arrange an interpreter to effectively communicate the report to you. Public availability Copies of the Department of Energy and Water Supply (DEWS) annual report are available online at www.dews.qld.gov.au. Limited printed copies are available by calling 13 QGOV. Enquiries about this publication should be directed to the Principal Planning and Governance Officer, Planning, Performance and Governance, DEWS. Email: [email protected] Phone: 07 3033 0534 This publication has been compiled by Planning and Performance, Business Corporate Partnerships in the Department of Agriculture, Fisheries and Forestry for the Department of Energy and Water Supply. © State of Queensland, 2013. The Queensland Government supports and encourages the dissemination and exchange of its information. The copyright in this publication is licensed under a Creative Commons Attribution 3.0 Australia (CC BY) licence. Under this licence you are free, without having to seek our permission, to use this publication in accordance with the licence terms. You must keep intact the copyright notice and attribute the State of Queensland as the source of the publication. Note: Some content in this publication may have different licence terms as indicated. For more information on this licence, visit http://creativecommons.org/licenses/by/3.0/au/deed.en. Contents Letter of compliance ...................................................................................................................................................................2 Director-General’s message ........................................................................................................................................................
    [Show full text]
  • Powerlink Queensland
    Powerlink Queensland Transmission Annual Planning Report 2016 Please direct Transmission Annual Planning Report enquiries to: Stewart Bell Group Manager Strategy and Planning Investment and Planning Division Powerlink Queensland Telephone: (07) 3860 2374 Email: [email protected] Disclaimer: While care is taken in the preparation of the information in this report, and it is provided in good faith, Powerlink Queensland accepts no responsibility or liability for any loss or damage that may be incurred by persons acting in reliance on this information or assumptions drawn from it. Contents Transmission Annual Planning Report 2016 Executive Summary _________________________________________________________________________________________________ 7 1. Introduction _________________________________________________________ 13 1.1 Introduction ________________________________________________________________________________ 14 1.2 Context of the Transmission Annual Planning Report _______________________________________ 14 1.3 Purpose of the Transmission Annual Planning Report _______________________________________ 15 1.4 Role of Powerlink Queensland ______________________________________________________________ 15 1.5 Overview of approach to asset management _______________________________________________ 16 1.6 Overview of planning responsibilities and processes ________________________________________ 16 1.6.1 Planning criteria and processes _______________________________________________________________ 16 1.6.2 Integrated planning of the
    [Show full text]
  • Annu Al Repor T 20 16
    INFIGEN ENERGY INFIGEN ENERGY RENEWABLE ENERGY FOR FUTURE GENERATIONS Infigen Energy Annual Report 2016 | ANNUAL REPORT 2016 REPORT | ANNUAL CONTENTS Who We Are 2 Infigen Management 26 Directors' Declaration 110 2016 Highlights 4 Corporate Structure 28 Independent Auditor's Report 111 Chairman's Report 6 Directors' Report 30 Additional Investor Information 113 Managing Director's Report 8 Remuneration Report 35 Glossary 116 Management Discussion and Analysis 10 Auditor's Independence Declaration 48 Corporate Directory 117 Infigen Board 24 Consolidated Financial Statements 49 OUR COMMITMENTS We plan and act to protect the health and wellbeing of our people, ensuring we operate our facilities safely and the environment is not harmed by our activities. We measure our environmental, social and corporate governance performance (ESG) against our sustainability targets.1 SECURITYHOLDERS EMPLOYEES COMMUNITY CUSTOMERS To generate economic To provide a safe, To foster respectful, To provide competitive value whilst acting on enjoyable, rewarding responsive and renewable energy climate change. and inclusive work enduring relationships. products and services. environment. All figures in this report relate to businesses of the Infigen Energy Group (“Infigen” or “the Group”), being Infigen Energy Limited (“IEL”), Infigen Energy Trust (“IET”) and Infigen Energy (Bermuda) Limited (“IEBL”) and the subsidiary entities of IEL and IET, for the year ended 30 June 2016 compared with the year ended 30 June 2015 (“prior year” or “prior corresponding period”) except where otherwise stated. All references to $ are a reference to Australian dollars unless specifically marked otherwise. Individual items and totals are rounded to the nearest appropriate number or decimal. Some totals may not add down the column due to rounding of individual components.
    [Show full text]
  • Green Infrastructure List
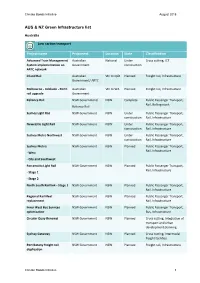
    Climate Bonds Initiative August 2018 AUS & NZ Green Infrastructure list Australia Low carbon transport Project name Proponent Location State Classification Advanced Train Management Australian National Under Cross cutting, ICT System implementation on Government construction ARTC network Inland Rail Australian VIC to QLD Planned Freight rail, Infrastructure Government/ ARTC Melbourne - Adelaide - Perth Australian VIC to WA Planned Freight rail, Infrastructure rail upgrade Government Reliance Rail NSW Government/ NSW Complete Public Passenger Transport, Rail, Rolling stock Reliance Rail Sydney Light Rail NSW Government NSW Under Public Passenger Transport, construction Rail, Infrastructure Newcastle Light Rail NSW Government NSW Under Public Passenger Transport, construction Rail, Infrastructure Sydney Metro Northwest NSW Government NSW Under Public Passenger Transport, construction Rail, Infrastructure Sydney Metro: NSW Government NSW Planned Public Passenger Transport, Rail, Infrastructure - West - City and Southwest Parramatta Light Rail NSW Government NSW Planned Public Passenger Transport, Rail, Infrastructure - Stage 1 - Stage 2 North South Rail link - Stage 1 NSW Government NSW Planned Public Passenger Transport, Rail, Infrastructure Regional Rail Fleet NSW Government NSW Planned Public Passenger Transport, replacement Rail, Infrastructure Inner West Bus Services NSW Government NSW Planned Public Passenger Transport, optimisation Bus, Infrastructure Circular Quay Renewal NSW Government NSW Planned Cross cutting, Integration of transport
    [Show full text]
  • Pvin Australia 2010
    PV IN AUSTRALIA 2010 Prepared for the International Energy Agency Cooperative Programme on PV Power Systems by Australian PV Association May 2011 AUTHORS: Dr Muriel Watt & Dr Robert Passey, IT Power (Australia) Warwick Johnston, SunWiz With support from June, 2011 Australian National Photovoltaics Status Report 2010 INTERNATIONAL ENERGY AGENCY CO-OPERATIVE PROGRAMME ON PHOTOVOLTAIC POWER SYSTEMS Task 1 Exchange and dissemination of information on PV power systems National Survey Report of PV Power Applications in Australia, 2010 ACKNOWLEGEMENTS This report is prepared on behalf of and with considerable input from members of the Australian PV Association (APVA) and the wider Australian PV sector. The objective of the APVA is to encourage participation of Australian organisations in PV industry development, policy analysis, standards and accreditation, advocacy and collaborative research and development projects concerning solar photovoltaic electricity. APVA provides: Up to date information on PV developments around the world (research, product development, policy, marketing strategies) as well as issues arising. A network of PV industry, government and researchers which undertake local and international PV projects, with associated shared knowledge and understanding. Australian input to PV guidelines and standards development. Management of Australian participation in IEA-PVPS, including: PV Information Exchange and Dissemination; PV Hybrid Systems within Mini-grids High Penetration PV in Electricity Grids. The Association receives funding from the Australian Solar Institute, to assist with the costs of IEA PVPS membership, Task activities and preparation of this report. COPYRIGHT This report is copyright of the Australian PV Association. The information contained therein may freely be used but all such use should cite the source as “Australian PV Survey Report 2010, APVA, May, 2011”.
    [Show full text]
  • Report to AEMC 2008-12-17
    ROAM Consulting Pty Ltd A.B.N. 54 091 533 621 Report (Emc00007) to NATIONAL ELECTRICITY MARKET DEVELOPMENT Market impacts of CPRS and RET 17 December 2008 Report to: NEM DEVELOPMENT Market impacts of CPRS and RET Emc00007 17 December 2008 VERSION HISTORY Version History Approved Date Revision Date Issued Prepared By Revision Type By Approved Richard Bean Joel Gilmore 0.5 2008-11-04 Jenny Riesz Ian Rose 2008-11-04 Draft Andrew Turley Ben Vanderwaal Richard Bean Joel Gilmore 1 2008-11-13 Jenny Riesz Ian Rose 2008-11-13 Report Andrew Turley Ben Vanderwaal Richard Bean Joel Gilmore 1.1 2008-11-14 Jenny Riesz Ian Rose 2008-11-14 Final revisions Andrew Turley Ben Vanderwaal Richard Bean Joel Gilmore Version for 1.2 2008-12-16 Jenny Riesz Ian Rose 2008-12-16 public release Andrew Turley Ben Vanderwaal Richard Bean Joel Gilmore Final version 1.3 2008-12-17 Jenny Riesz Ian Rose 2008-12-17 for public Andrew Turley release Ben Vanderwaal ROAM Consulting Pty Ltd VERSION HISTORY www.roamconsulting.com.au Report to: NEM DEVELOPMENT Market impacts of CPRS and RET Emc00007 17 December 2008 EXECUTIVE SUMMARY This report discusses issues surrounding the introduction of the RET and CPRS in the Australian electricity market that have been revealed by ROAM’s modelling. The material issues are as follows. Review of modelling studies Three main reports have been identified by ROAM to provide insight into the impacts of the CPRS and the RET upon the electricity sector. These are: 1. Impacts of the Carbon Pollution Reduction Scheme on Australia’s electricity markets , Report to Federal Treasury by McLennan Magasanik Associates (MMA) .
    [Show full text]
  • Dr Michael I. Cleary Associate Professor of Medicine
    DMZ.900.001.0080 EXHIBIT 40 Dr Michael I. Cleary Associate Professor of Medicine Health appointments Chief Operations Officer Department of Health and July 2012 - current Deputy Director-General, Health Service & Clinical Innovation Division Acting Director-General February 2015-July 2015 Queensland Department of Health (periodic relief February 2013 - January 2015) Deputy Director-General Polley, Strategy & Resourcing Division May 2010 - July 2012 Queensland Department of Health Executive Director and Director of Medical Services December 2009 - May 2010 Logan and Beaudesert Hospitals Executive Director of Medical Services April 2006 - December 2009 Southside Health Service District Executive Director of Medical Services April 2000 - April 2006 The Prince Charles Hospital & Health Service District Acting District Manager September 2003-Aprll 2004; August 2005 -April 2006 The Prince Charles Hospital and Health Service District Acting District Manager May 2005 Bundaberg Health Service District Acting Executive Director of Medical Services March 1999 - December 1999 Toowoomba Health Service District Acting Executive Director of Medical Services July 1998- February 1999 Princess Alexandra Hospital Director of Medical Administration July 1997- March 2000 Princess Alexandra Hospital Medical Advisor, Division of Policy & Planning Manager February 1996-July 1997 Elective Surgery Team, Queensland Health Medical Superintendent September 1996 - July 1997 Queen Elizabeth II Hospital Acting Director Division of Emergency Medicine & Ambulatory Care May 1994-July 1995 Royal Brisbane Hospital Staff Specialist Department of Emergency Medicine & Ambulatory Care 1989-1996 · Royal Brisbane Hospital Acting Director of Emergency Medicine August 1989 Queen Elizabeth II Jubilee Hospital Emergency Physician nn.,i•i"u" 011~111::\..1a111;)u . Priority Emergency Centre Mater Private """"''""' 1 ~"' ' Page 2 of 3 25 DMZ.900.001.0081 EXHIBIT 40 Dr Michael I.
    [Show full text]
  • Bill Appropriation Bill Community Ambulance
    2066 Approp. Bills; Comm. Amb. Cover Levy Repeal & Rev. & O’r Leg. A’ment Bill 17 Jun 2011 invested in a service that is there to keep each and every one of us safe at the peril of those individual officers. What you see in this budget is an additional investment in order to put GPS tracking into Corrective Services to ensure community safety is enhanced. There are also investments in the vehicle fleet for the Police Service to ensure the fleet is upgraded and maintained. There is an opportunity to make further investments into the future for such things as the technology the member is talking about, and that will be taken seriously in each budget process. The member’s question goes directly to an interest in public service delivery—the sort of public service delivery that the opposition wants to cut out from those on the Sunshine Coast, who have a legitimate expectation that the full $2 billion that was put into the Capital Statement should be kept for the Sunshine Coast. I make a prediction here that we will not see the ridiculous concept of Campbell Newman standing in front of someone at a press conference today; in fact, I do not think we will see him at all today. I think he would have scarpered. He will be running at a million miles an hour. He will be running around up there on level 6, up on tippy-toes, waving his arms around, projecting himself, pointing fingers and blaming people, hopping into all the staff members, getting into the shadow Treasurer, saying to the Leader of the Opposition that it is his fault, doing a nana.
    [Show full text]
  • Renewable Energy
    Chapter 7: Renewable energy 7.1 Introduction 7.2 Network capacity for new generation 7.3 Supporting renewable energy infrastructure development 7.4 Further information 7 Renewable energy Key highlights yyThis chapter explores the potential for the development and connection of renewable energy generation to Powerlink’s transmission network. yyThe generation connection capacity of Powerlink’s 132kV and 110kV substations for the existing transmission network is identified to facilitate high level decision making for interested parties. yyCompared to most other States in the NEM, Queensland’s network presently has a much lower proportion of intermittent renewables (to total generation capacity) and is capable of accommodating a considerable number of additional renewable connections without immediate concern for overall system stability. yyWhere economies of scale can be achieved through project cluster, Powerlink may consider the development of Renewable Energy Zones (REZs), subject to regulatory approvals and the conditions of its Transmission Licence. 7.1 Introduction Queensland is rich in a diverse range of renewable energy resources – geothermal, biomass, wind and hydro – however the focus to date has been on solar, with Queensland displaying amongst the highest levels of solar concentration in the world. This makes Queensland an attractive location for large‑scale solar powered generation development projects. There is significant potential for energy supply from renewable resources in Queensland. The rapid uptake of renewable energy systems is stimulating the development of supporting technologies, which in turn is improving the affordability of these systems. The uptake of over 1,500MW of small‑scale solar in Queensland to date provides strong indication that Queensland consumers are no longer meeting their energy requirements entirely through conventional means.
    [Show full text]
  • CS Energy Annual Report 2010/2011 2010/2011 in Review
    Annual Report 2010/2011 Table of contents 2010/2011 in review About CS Energy Inside front cover Highlights 2010/2011 2 Performance against measures 4 Chairman’s review 6 Chief Executive’s review 8 Corporate performance Finance 10 Market 12 Portfolio 14 People 16 Social Licence 22 Portfolio performance Callide Power Station 26 Kogan Creek Power Station 30 Mica Creek Power Station 34 Swanbank Power Station 38 Corporate Governance Report 42 Board of Directors profiles 48 Executive Management Team profiles 52 Financial Report 54 Directors’ Report 55 Auditor’s Independence Declaration 61 Statement of Comprehensive Income 62 Notes to the Financial Statements 67 Directors’ Declaration 116 Independent Auditor’s Report 117 esaa Sustainable Principles table 118 Index 120 Glossary Inside back cover CS Energy Annual Report 2010/2011 2010/2011 in review About this report About CS Energy The 2010/2011 Annual Report outlines our operational, Last year, we produced our first combined Annual CS Energy is a Queensland Government owned energy provider and financial, economic, environmental and social performance Report and Sustainability Report following a Corporate as at 30 June 2011, we had 638 employees across four power station for the financial year 1 July 2010 to 30 June 2011. This Responsibility and Sustainability Review in 2009. sites and a corporate office, and we had a generation capacity of is CS Energy Limited’s (CS Energy’s) second combined CS Energy is committed to embedding sustainability within 3,165 megawatts. Annual Report and Sustainability Report. all of our business practices, and our progress towards this CS Energy supplied approximately 30 per cent of Queensland’s The Annual Report provides key performance information goal is outlined in this report.
    [Show full text]
  • 2010 PV in Australia Report (Pdf)
    PV IN AUSTRALIA 2010 Prepared for the International Energy Agency Cooperative Programme on PV Power Systems by Australian PV Association May 2011 AUTHORS: Dr Muriel Watt & Dr Robert Passey, IT Power (Australia) Warwick Johnston, SunWiz With support from June, 2011 Australian National Photovoltaics Status Report 2010 INTERNATIONAL ENERGY AGENCY CO-OPERATIVE PROGRAMME ON PHOTOVOLTAIC POWER SYSTEMS Task 1 Exchange and dissemination of information on PV power systems National Survey Report of PV Power Applications in Australia, 2010 ACKNOWLEGEMENTS This report is prepared on behalf of and with considerable input from members of the Australian PV Association (APVA) and the wider Australian PV sector. The objective of the APVA is to encourage participation of Australian organisations in PV industry development, policy analysis, standards and accreditation, advocacy and collaborative research and development projects concerning solar photovoltaic electricity. APVA provides: Up to date information on PV developments around the world (research, product development, policy, marketing strategies) as well as issues arising. A network of PV industry, government and researchers which undertake local and international PV projects, with associated shared knowledge and understanding. Australian input to PV guidelines and standards development. Management of Australian participation in IEA-PVPS, including: PV Information Exchange and Dissemination; PV Hybrid Systems within Mini-grids High Penetration PV in Electricity Grids. The Association receives funding from the Australian Solar Institute, to assist with the costs of IEA PVPS membership, Task activities and preparation of this report. COPYRIGHT This report is copyright of the Australian PV Association. The information contained therein may freely be used but all such use should cite the source as “Australian PV Survey Report 2010, APVA, May, 2011”.
    [Show full text]