DOCSLIB.ORG

List of Logic Symbols

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
List of Logic Symbols List of logic symbols In logic, a set of symbols is commonly used to express logical representation. The following table lists many common symbols together with their name, pronunciation, and the related field of mathematics. Additionally, the third column contains an informal definition, the fourth column gives a short example, the fifth and sixth give the unicode location and name for use in HTML documents.[1] The last column provides the LaTeX symbol. 1 Basic logic symbols Name Unicode HTML H Symbol Read as Explanation Examples Value Value E Category (hexdecimal) (decimal) (n A ⇒ B is true only in the case that material either A is implication false or B is true. → may mean ⇒ the same as ⇒ (the symbol implies; if .. U+21D2 &#8658; &rA may also x = 2 ⇒ x2 = 4 is true, then indicate the but x2 = 4 ⇒ x = 2 is U+2192 &#8594; &r → domain and in general false (since codomain of a x could be −2). U+2283 &#8835; &s function; see table of ⊃ mathematical symbols). propositional logic, Heyting ⊃ may mean algebra the same as ⇒ (the symbol may also mean superset). ⇔ material equivalence A ⇔ B is true U+21D4 &#8660; &hA if and only if; only if both A x + 5 = y + 2 ⇔ x + 3 = iff; means the and B are false, U+2261 &#8801; &e ≡ y same as or both A and B are true. U+2194 &#8596; &h propositional ↔ logic negation The statement ¬(¬A) ⇔ A U+00AC &#172; &n ¬ ¬A is true if x ≠ y ⇔ ¬(x = y) and only if A is U+02DC &#732; &t false. not U+0021 &#33; &ex ˜ A slash placed through another propositional operator is the logic ! same as "¬" placed in front. Name Unicode HTML H Symbol Read as Explanation Examples Value Value E Category (hexdecimal) (decimal) (n ∧ logical conjunction The statement U+2227 &#8743; &a and A ∧ B is true if n < 4 ∧ n >2 ⇔ n = 3 · A and B are when n is a natural U+00B7 &#183; &m propositional both true; else number. logic, it is false. U+0026 &#38; &am Boolean & algebra logical ∨ (inclusive) disjunction The statement or A ∨ B is true if U+2228 &#8744; &o A or B (or both) n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3 + are true; if both when n is a natural U+002B &#43; propositional are false, the number. logic, statement is U+2225 &#8741; Boolean false. algebra ∥ exclusive The statement (¬A) ⊕ A is always U+2295 &#8853; &o disjunction A ⊕ B is true true, and A ⊕ A always xor when either A false, if vacuous truth U+22BB &#8891; ⊕ or B, but not is excluded. propositional both, are true. logic, A ⊻ B means Boolean the same. ⊻ algebra Tautology ⊤ top, verum The statement U+22A4 &#8868; ⊤ is A ⇒ ⊤ is always true. T propositional unconditionally logic, true. Boolean algebra 1 Name Unicode HTML H Symbol Read as Explanation Examples Value Value E Category (hexdecimal) (decimal) (n Contradiction ⊥ bottom, falsum, The statement falsity ⊥ is U+22A5 &#8869; &p unconditionally F false. (The ⊥ ⇒ A is always true. propositional symbol ⊥ may logic, also refer to Boolean perpendicular algebra lines.) 0 universal ∀ x: P(x) or ∀ n ∈ ℕ: n2 ≥ n. U+2200 &#8704; &f ∀ quantification (x) P(x) means for all; for any; for each P(x) is true for all x. first-order () logic existential ∃ x: P(x) quantification means there is ∃ there exists at least one x ∃ n ∈ ℕ: n is even. U+2203 &#8707; &ex first-order such that P(x) logic is true. uniqueness quantification ∃! x: P(x) means there is there exists &#8707; exactly one x ∃! n ∈ ℕ: n + 5 = 2n. U+2203 U+0021 ∃! exactly one &#33; such that P(x) first-order is true. logic Name Unicode HTML H Symbol Read as Explanation Examples Value Value E Category (hexdecimal) (decimal) (n definition x ≔ y or x ≡ y is defined as means x is defined to be ≔ another name for y (but note &#8788; U+2254 that ≡ can also cosh x ≔ (1/2)(exp x + (&#58; (U+003A U+003D) mean other exp (−x)) &#61;) things, such as ≡ U+2261 &e congruence). everywhere A XOR B :⇔ &#8801; (A ∨ B) ∧ ¬(A ∧ B) U+003A U+229C &hA P :⇔ Q means &#8860; :⇔ P is defined to be logically equivalent to Q. precedence Perform the (8 ÷ 4) ÷ 2 = 2 ÷ 2 = 1, U+0028 U+0029 &#40; ( ) grouping operations but 8 ÷ (4 ÷ 2) = 8 ÷ &#41; parentheses, inside the 2 = 4. brackets parentheses everywhere first. Turnstile x ⊢ y means y is provable provable from x (in A → B ⊢ ¬B → ¬A U+22A2 &#8866; ⊢ propositional some specified logic, first- formal order logic system). double turnstile x ⊨ y means x entails ⊨ semantically A → B ⊨ ¬B → ¬A U+22A8 &#8872; propositional entails y logic, first- order logic Name Unicode HTML H Symbol Read as Explanation Examples Value Value E Category (hexdecimal) (decimal) (n 2 Advanced and rarely used logical symbols These symbols are sorted by their Unicode value: U+00B7 · MIDDLE DOT, an outdated way for denoting AND,[3] still in use in electronics; for example "A · B" is the same as "A & B" · : Center dot with a line above it; outdated way for denoting NAND, for example "A·B" is the same as "A NAND B" or "A | B" or "¬ (A & B)". See also Unicode U+22C5 ⋅ . U+0305 ̅ COMBINING OVERLINE, used as abbreviation for standard numerals (Typographical Number Theory). For example, using HTML style "4̅" is a shorthand for the standard numeral "SSSS0". Overline is also a rarely used format for denoting Gödel numbers: for example, "A V B" says the Gödel number of "(A V B)". Overline is also an outdated way for denoting negation, still in use in electronics: for example, "A V B" is the same as "¬(A V B)". U+2191 ↑ UPWARDS ARROW or U+007C | VERTICAL LINE: Sheffer stroke, the sign for the NAND operator. U+2193 ↓ DOWNWARDS ARROW Peirce Arrow, the sign for the NOR operator. U+2201 ∁ C U+2204 ∄ THERE DOES NOT EXIST: strike out existential quantifier same as "¬∃" U+2234 ∴ T: Therefore U+2235 ∵ B: because U+22A7 ⊧ M: is a model of U+22A8 ⊨ T: is true of U+22AC ⊬ DOES NOT PROVE: negated ⊢, the sign for "does not prove", for example T ⊬ P says "P is not a theorem of T" U+22AD ⊭ N : is not true of U+22BC ⊼ NAND: NAND operator. In HTML, it can also be produced by <span style="text-decoration: overline">&and;</span> : ∧ U+22BD ⊽ N: NOR operator. In HTML, it can also be produced by <span style="text-decoration: overline">&or;</span> : ∨ U+25C7 ◇ WHITE DIAMOND: modal operator for "it is possible that", "it is not necessarily not" or rarely "it is not provable not" (in most modal logics it is defined as "¬◻¬") U+22C6 ⋆ STAR OPERATOR: usually used for ad-hoc operators U+22A5 ⊥ UP TACK or U+2193 ↓ DOWNWARDS ARROW: Webb-operator or Peirce arrow, the sign for NOR. Confusingly, "⊥" is also the sign for contradiction or absurdity. U+2310 ⌐ REVERSED NOT SIGN U+231C ⌜ TOP LEFT CORNER and U+231D ⌝ TOP RIGHT CORNER: corner quotes, also called "Quine quotes"; for quasi-quotation, i.e. quoting specific context of unspecified ("variable") expressions;[4] also used for denoting Gödel number;[5] for example "⌜G⌝" denotes the Gödel number of G. (Typographical note: although the quotes appears as a "pair" in unicode (231C and 231D), they are not symmetrical in some fonts. And in some fonts (for example Arial) they are only symmetrical in certain sizes. Alternatively the quotes can be rendered as ⌈ and ⌉ (U+2308 and U+2309) or by using a negation symbol and a reversed negation symbol ⌐ ¬ in superscript mode. ) U+25FB ◻ WHITE MEDIUM SQUARE or U+25A1 □ WHITE SQUARE: modal operator for "it is necessary that" (in modal logic), or "it is provable that" (in provability logic), or "it is obligatory that" (in deontic logic), or "it is believed that" (in doxastic logic); also as empty clause (alternatives: and ⊥). Note that the following operators are rarely supported by natively installed fonts. If you wish to use these in a web page, you should always embed the necessary fonts so the page viewer can see the web page without having the necessary fonts installed in their computer. U+27E1 ⟡ WHITE CONCAVE-SIDED DIAMOND U+27E2 ⟢ WHITE CONCAVE-SIDED DIAMOND WITH LEFTWARDS TICK: modal operator for was never U+27E3 ⟣ WHITE CONCAVE-SIDED DIAMOND WITH RIGHTWARDS TICK: modal operator for will never be U+27E4 ⟤ WHITE SQUARE WITH LEFTWARDS TICK: modal operator for was always U+27E5 ⟥ WHITE SQUARE WITH RIGHTWARDS TICK: modal operator for will always be U+297D RIGHT FISH TAIL: sometimes used for "relation", also used for denoting various ad hoc relations (for example, for denoting "witnessing" in the context of Rosser's trick) The fish hook is also used as strict implication by C.I.Lewis , the corresponding LaTeX macro is \strictif. See here for an image of glyph. Added to Unicode 3.2.0. U+2A07 ⨇ TWO LOGICAL AND OPERATOR 2.1 Poland and Germany As of 2014 in Poland, the universal quantifier is sometimes written and the existential quantifier as . The same applies for Germany.[6] 3 See also Józef Maria Bocheński List of notation used in Principia Mathematica List of mathematical symbols Logic alphabet, a suggested set of logical symbols Logical connective Mathematical operators and symbols in Unicode Polish notation Truth function Truth table 4 References 1. "Named character references" . HTML 5.1 Nightly. W3C. Retrieved 9 September 2015. 2. Although this character is available in LaTeX, the MediaWiki TeX system doesn't support this character. 3. Brody, Baruch A.
Load more

Recommended publications
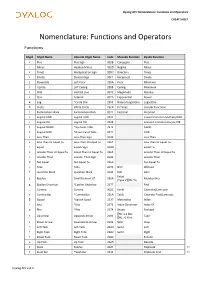
  • Dyalog APL Binding Strengths
    Dyalog APL Nomenclature: Functions and Operators CHEAT SHEET Nomenclature: Functions and Operators Functions Glyph Glyph Name Unicode Glyph Name Code Monadic Function Dyadic Function + Plus Plus Sign 002B Conjugate Plus - Minus Hyphen-Minus 002D Negate Minus × Times Multiplication Sign 00D7 Direction Times ÷ Divide Division Sign 00F7 Reciprocal Divide ⌊ Downstile Left Floor 230A Floor Minimum ⌈ Upstile Left Ceiling 2308 Ceiling Maximum | Stile Vertical Line 007C Magnitude Residue * Star Asterisk 002A Exponential Power ⍟ Log *Circle Star 235F Natural Logarithm Logarithm ○ Circle White Circle 25CB Pi Times Circular Functions ! Exclamation Mark Exclamation Mark 0021 Factorial Binomial ∧ Logical AND Logical AND 2227 Lowest Common Multiple/AND ∨ Logical OR Logical OR 2228 Greatest Common Divisor/OR ⍲ Logical NAND *Up Caret Tilde 2372 NAND ⍱ Logical NOR *Down Caret Tilde 2371 NOR < Less Than Less-Than Sign 003C Less Than ≤ Less Than Or Equal To Less-Than Or Equal To 2264 Less Than Or Equal To = Equal Equals Sign 003D Equal To ≥ Greater Than Or Equal To Great-Than Or Equal To 2265 Greater Than Or Equal To > Greater Than Greater-Than Sign 003E Greater Than ≠ Not Equal Not Equal To 2260 Not Equal To ~ Tilde Tilde 007E NOT Without ? Question Mark Question Mark 003F Roll Deal Enlist ∊ Epsilon Small Element Of 220A Membership (Type if ⎕ML=0) ⍷ Epsilon Underbar *Epsilon Underbar 2377 Find , Comma Comma 002C Ravel Catenate/Laminate ⍪ Comma Bar *Comma Bar 236A Table Catenate First/Laminate ⌷ Squad *Squish Quad 2337 Materialise Index ⍳ Iota *Iota 2373
    [Show full text]
  • The Unicode Cookbook for Linguists: Managing Writing Systems Using Orthography Profiles
    Zurich Open Repository and Archive University of Zurich Main Library Strickhofstrasse 39 CH-8057 Zurich www.zora.uzh.ch Year: 2017 The Unicode Cookbook for Linguists: Managing writing systems using orthography profiles Moran, Steven ; Cysouw, Michael DOI: https://doi.org/10.5281/zenodo.290662 Posted at the Zurich Open Repository and Archive, University of Zurich ZORA URL: https://doi.org/10.5167/uzh-135400 Monograph The following work is licensed under a Creative Commons: Attribution 4.0 International (CC BY 4.0) License. Originally published at: Moran, Steven; Cysouw, Michael (2017). The Unicode Cookbook for Linguists: Managing writing systems using orthography profiles. CERN Data Centre: Zenodo. DOI: https://doi.org/10.5281/zenodo.290662 The Unicode Cookbook for Linguists Managing writing systems using orthography profiles Steven Moran & Michael Cysouw Change dedication in localmetadata.tex Preface This text is meant as a practical guide for linguists, and programmers, whowork with data in multilingual computational environments. We introduce the basic concepts needed to understand how writing systems and character encodings function, and how they work together. The intersection of the Unicode Standard and the International Phonetic Al- phabet is often not met without frustration by users. Nevertheless, thetwo standards have provided language researchers with a consistent computational architecture needed to process, publish and analyze data from many different languages. We bring to light common, but not always transparent, pitfalls that researchers face when working with Unicode and IPA. Our research uses quantitative methods to compare languages and uncover and clarify their phylogenetic relations. However, the majority of lexical data available from the world’s languages is in author- or document-specific orthogra- phies.
    [Show full text]
  • The Unicode Standard 5.2 Code Charts
    Miscellaneous Technical Range: 2300–23FF The Unicode Standard, Version 5.2 This file contains an excerpt from the character code tables and list of character names for The Unicode Standard, Version 5.2. Characters in this chart that are new for The Unicode Standard, Version 5.2 are shown in conjunction with any existing characters. For ease of reference, the new characters have been highlighted in the chart grid and in the names list. This file will not be updated with errata, or when additional characters are assigned to the Unicode Standard. See http://www.unicode.org/errata/ for an up-to-date list of errata. See http://www.unicode.org/charts/ for access to a complete list of the latest character code charts. See http://www.unicode.org/charts/PDF/Unicode-5.2/ for charts showing only the characters added in Unicode 5.2. See http://www.unicode.org/Public/5.2.0/charts/ for a complete archived file of character code charts for Unicode 5.2. Disclaimer These charts are provided as the online reference to the character contents of the Unicode Standard, Version 5.2 but do not provide all the information needed to fully support individual scripts using the Unicode Standard. For a complete understanding of the use of the characters contained in this file, please consult the appropriate sections of The Unicode Standard, Version 5.2, online at http://www.unicode.org/versions/Unicode5.2.0/, as well as Unicode Standard Annexes #9, #11, #14, #15, #24, #29, #31, #34, #38, #41, #42, and #44, the other Unicode Technical Reports and Standards, and the Unicode Character Database, which are available online.
    [Show full text]
  • Logic and Artificial Intelligence
    Logic and Artificial Intelligence: Divorced,StillMarried,Separated...?∗ Selmer Bringsjord//David A. Ferrucci February 13, 1998 Abstract Though it’s difficult to agree on the exact date of their union, logic and artificial intelligence (AI) were married by the late 1950s, and, at least during their honeymoon, were happily united. What connubial permu- tation do logic and AI find themselves in now? Are they still (happily) married? Are they divorced? Or are they only separated, both still keep- ing alive the promise of a future in which the old magic is rekindled? This paper is an attempt to answer these questions via a review of six books. Encapsulated, our answer is that (i) logic and AI, despite tabloidish re- ports to the contrary, still enjoy matrimonial bliss, and (ii) only their future robotic offspring (as opposed to the children of connectionist AI) will mark real progress in the attempt to understand cognition. 1 The Logic–AI Marriage Though it’s difficult to agree on the exact date of their union, logic and artificial intelligence (AI) were married by the late 1950s, and, at least during their honeymoon, were happily married. But what connubial permutation do logic and AI find themselves in now? Are they still (happily) married? Are they divorced? Or are they only separated, both still keeping alive the promise of a future in which the old magic is rekindled? This paper is an attempt to answer these questions via a review of the following six books: • Ronald J. Brachman, Hector J. Levesque, and Raymond Reiter, eds., Knowledge Representation, Special Issues of Artificial Intelligence: An International Journal, Cambridge, MA: MIT Press, 1992, 408 pp., $29.00 (paper), ISBN 0-262-52168-7.
    [Show full text]
  • ISO/IEC JTC1/SC2/WG2 N 2005 Date: 1999-05-29
    ISO INTERNATIONAL ORGANIZATION FOR STANDARDIZATION ORGANISATION INTERNATIONALE DE NORMALISATION --------------------------------------------------------------------------------------- ISO/IEC JTC1/SC2/WG2 Universal Multiple-Octet Coded Character Set (UCS) -------------------------------------------------------------------------------- ISO/IEC JTC1/SC2/WG2 N 2005 Date: 1999-05-29 TITLE: ISO/IEC 10646-1 Second Edition text, Draft 2 SOURCE: Bruce Paterson, project editor STATUS: Working paper of JTC1/SC2/WG2 ACTION: For review and comment by WG2 DISTRIBUTION: Members of JTC1/SC2/WG2 1. Scope This paper provides a second draft of the text sections of the Second Edition of ISO/IEC 10646-1. It replaces the previous paper WG2 N 1796 (1998-06-01). This draft text includes: - Clauses 1 to 27 (replacing the previous clauses 1 to 26), - Annexes A to R (replacing the previous Annexes A to T), and is attached here as “Draft 2 for ISO/IEC 10646-1 : 1999” (pages ii & 1 to 77). Published and Draft Amendments up to Amd.31 (Tibetan extended), Technical Corrigenda nos. 1, 2, and 3, and editorial corrigenda approved by WG2 up to 1999-03-15, have been applied to the text. The draft does not include: - character glyph tables and name tables (these will be provided in a separate WG2 document from AFII), - the alphabetically sorted list of character names in Annex E (now Annex G), - markings to show the differences from the previous draft. A separate WG2 paper will give the editorial corrigenda applied to this text since N 1796. The editorial corrigenda are as agreed at WG2 meetings #34 to #36. Editorial corrigenda applicable to the character glyph tables and name tables, as listed in N1796 pages 2 to 5, have already been applied to the draft character tables prepared by AFII.
    [Show full text]
  • ERGOAI Reasoner User's Manual
    ERGOAI Reasoner User’s Manual Version 2.0 (Myia) Edited by Michael Kifer Coherent Knowledge October 2018 Portions Copyright © 2013–2018 Coherent Knowledge CONTENTS Contents 1 Introduction 1 2 Installation 1 3 Running ERGO 2 4 ERGO Shell Commands 3 5 F-logic and ERGO by Example 10 6 Main Syntactic Elements of ERGO 10 7 Basic ERGO Syntax 13 7.1 F-logic Vocabulary ..................................... 13 7.2 Symbols, Strings, and Comments ............................. 18 7.3 Operators .......................................... 21 7.4 Logical Expressions ..................................... 23 7.5 Arithmetic (and related) Expressions ........................... 23 7.6 Quasi-constants and Quasi-variables ........................... 30 7.7 Synonyms .......................................... 31 7.8 Reserved Symbols ..................................... 31 8 Path Expressions 31 9 Set Notation 33 10 Typed Variables 34 11 Truth Values and Object Values 36 12 Boolean Methods 38 Portions Copyright © 2013–2018 Coherent Knowledge i CONTENTS 12.1 Boolean Signatures ..................................... 39 13 Skolem Symbols 39 14 Testing Meta-properties of Symbols and Variables 46 15 Lists, Sets, Ranges. The Operators \in, \subset, \sublist 50 16 Multifile Knowledge Bases 51 16.1 ERGO Modules ....................................... 52 16.2 Calling Methods and Predicates Defined in User Modules ............... 53 16.3 Finding the Current Module Name ............................ 55 16.4 Finding the Module That Invoked A Rule ........................ 55 16.5 Loading Files into User Modules ............................. 55 16.6 Adding Rule Bases to Existing Modules ......................... 58 16.7 Module References in Rule Heads ............................. 59 16.8 Calling Prolog Subgoals from ERGO ........................... 60 16.9 Calling ERGO from Prolog ................................. 62 16.9.1 Importing ERGO Predicates into Prolog ..................... 62 16.9.2 Passing Arbitrary Queries to ERGO ......................
    [Show full text]
  • Math 1090 Part Two: Predicate (First-Order) Logic
    Math 1090 Part two: Predicate (First-Order) Logic Saeed Ghasemi York University 5th July 2018 Saeed Ghasemi (York University) Math 1090 5th July 2018 1 / 95 Question. Is propositional logic rich enough to do mathematics and computer science? The answer is \Absolutely not"! Mathematics and computer science deals with structures like sets, strings, numbers, matrices, trees, graphs, programs, Turing machines and many others. The propositional logic is not rich enough to deal with this structures. For example, try expressing the statements \there is a rational number strictly between two given rational numbers" or \every natural number has a unique prime factorization". We cannot even express these statements in the Boolean Logic, let alone proving them! Saeed Ghasemi (York University) Math 1090 5th July 2018 2 / 95 Number Theory-Peano's Arithmetic In order to express formulas in number theory: We need to be able to refer to numbers, N = f1; 2; 3;::: g as variables. we need to have variable symbols that would refer to numbers, like n; m; n0;::: . Let's call them \object variables". We need to be able to say when two numbers are equal, that's why we need a symbol \=" for the equality between the variable objects. We need to be able to say expressions like \for all natural numbers ...". So let's have a symbol 8, which says \for all". We need a special constant denoting 0. We also need to be able to add and multiply numbers. So lets have function + : N × N ! N and × : N × N ! N for addition and multiplication, respectively (we say these functions have arity2 because they take two inputs, so the function f (x; y; z) = ::: has arity 3).
    [Show full text]
  • ISO/IEC International Standard 10646-1
    ISO/IEC 10646:2003/Amd.6:2009(E) Information technology — Universal Multiple-Octet Coded Character Set (UCS) — AMENDMENT 6: Bamum, Javanese, Lisu, Meetei Mayek, Samaritan, and other characters Page 2, Clause 3, Normative references Click on this highlighted text to access the reference file. Update the reference to the Unicode Bidirectional Algo- NOTE 5 – The content is also available as a separate view- rithm and the Unicode Normalization Forms as follows: able file in the same file directory as this document. The file is named: “CJKU_SR.txt”. Unicode Standard Annex, UAX#9, The Unicode Bidi- rectional Algorithm: Page 25, Clause 29, Named UCS Sequence http://www.unicode.org/reports/tr9/tr9-21.html. Identifiers Unicode Standard Annex, UAX#15, Unicode Normali- Insert the additional 290 sequence identifiers zation Forms: http://www.unicode.org/reports/tr15/tr15-31.html. <0B95, 0BCD> TAMIL CONSONANT K <0B99, 0BCD> TAMIL CONSONANT NG Page 14, Sub-clause 20.3, Format characters <0B9A, 0BCD> TAMIL CONSONANT C <0B9E, 0BCD> TAMIL CONSONANT NY Insert the following entry in the list of formats charac- <0B9F, 0BCD> TAMIL CONSONANT TT ters: <0BA3, 0BCD> TAMIL CONSONANT NN <0BA4, 0BCD> TAMIL CONSONANT T 110BD KAITHI NUMBER SIGN <0BA8, 0BCD> TAMIL CONSONANT N <0BAA, 0BCD> TAMIL CONSONANT P Page 20, Sub-clause 26.1, Hangul syllable <0BAE, 0BCD> TAMIL CONSONANT M composition method <0BAF, 0BCD> TAMIL CONSONANT Y <0BB0, 0BCD> TAMIL CONSONANT R <0BB2, 0BCD> TAMIL CONSONANT L Insert the following note after Note 2. <0BB5, 0BCD> TAMIL CONSONANT V NOTE 3 – Hangul text can be represented in several differ- <0BB4, 0BCD> TAMIL CONSONANT LLL ent ways in this standard.
    [Show full text]
  • Cabineta Quarterly of Art and Culture
    A QUARTERLY OF ART AND CULTURE ISSUE 18 FICTIONAL STATES CABINET US $10 CANADA $15 UK £6 inside this issue THERMIDOR 2005 Sasha Archibald • John Bear • Robert Blackson • William Bryk • Sasha Chavchavadze • Mark Dery • Allen Ezell • Charles Green • Invertebrate • Craig Kalpakjian • Peter Lamborn Wilson • David Levi Strauss • Brian McMullen • Glexis Novoa • George Pendle • Elizabeth Pilliod • Patrick Pound • Bonnie and Roger Riga • Lynne Roberts-Goodwin • Tal Schori • Cecilia Sjöholm • Frances Stark • Michael Taussig • Christopher Turner • Jonathan Ward • Christine Wertheim • Tony Wood • Shea Zellweger cabinet Cabinet is a non-profit 501 (c) (3) magazine published by Immaterial Incorporated. 181 Wyckoff Street Contributions to Cabinet are fully tax-deductible. Our survival is dependent on Brooklyn NY 11217 USA such contributions; please consider supporting us at whatever level you can. tel + 1 718 222 8434 Donations of $25 or more will be acknowledged in the next possible issue. Dona- fax + 1 718 222 3700 tions above $250 will be acknowledged for four issues. Checks should be made email [email protected] out to “Cabinet.” Please mark the envelope, “Rub your eyes before opening.” www.cabinetmagazine.org Cabinet wishes to thank the following visionary foundations and individuals Summer 2005, issue 18 for their support of our activities during 2005. Additionally, we will forever be indebted to the extraordinary contribution of the Flora Family Foundation from Editor-in-chief Sina Najafi 1999 to 2004; without their generous support, this publication would not exist. Senior editor Jeffrey Kastner Thanks also to the Andy Warhol Foundation for the Visual Arts for their two-year Editors Jennifer Liese, Christopher Turner grant in 2003-2004.
    [Show full text]
  • Feature Extraction with Description Logics Functional Subsumption
    Functional Subsumption in Feature Description Logic Rodrigo de Salvo Braz1 and Dan Roth2 1 [email protected] 2 [email protected] Department of Computer Science University of Illinois at Urbana-Champaign 201 N. Goodwin Urbana, IL 61801-2302 Summary. Most machine learning algorithms rely on examples represented propo- sitionally as feature vectors. However, most data in real applications is structured and better described by sets of objects with attributes and relations between them. Typically, ad-hoc methods have been used to convert such data to feature vectors, taking, in many cases, a significant amount of the computation. Propositionaliza- tion becomes more principled if generating features from structured data is done using a formal, domain independent language that describes feature types to be extracted. This language must have limited expressivity in order to be useful while some inference procedures on it are still tractable. In this chapter we present Feature Description Logic (FDL), proposed by Cumby & Roth, where feature extraction is viewed as an inference process (subsumption). We also present an extension to FDL we call Functional FDL. FDL is ultimately based on the unification of object attributes and relations between objects in or- der to detect feature types in examples. Functional subsumption provides further abstraction by using unification modulo a Boolean function representing similar- ity between attributes and relations. This greatly improves flexibility in practical situations by accomodating variations in attributes values and relation names, in- corporating background knowledge (e.g., typos, number and gender, synomyms etc). We define the semantics of Functional subsumption and how to adapt the regular subsumption algorithm for implementing it.
    [Show full text]
  • Universal Multiple-Octet Coded Character Set (UCS) —
    ISO/IEC JTC1 SC2/WG2 N2845 all Final Proposed Draft Amendment (FPDAM) 1 ISO/IEC 10646:2003/Amd.1:2004 (E) Information technology — Universal Multiple-Octet Coded Character Set (UCS) — AMENDMENT 1: Glagolitic, Coptic, Georgian and other characters In the definition of Graphic character (formerly sub- Page 1, Clause 1 Scope clause 4.20, now 4.22), insert “or a format character” In the note, update the Unicode Standard version after “control function”. from 4.0 to 4.1. Page 2, Clause 3 Normative references Page 14, Clause 19 Characters in bidirectional context Update the reference to the Unicode Bidirectional Algorithm and the Unicode Normalization Forms as Add ‘Mirrored’ before ‘Character’ in clause title and follows: replace the text of the clause by the following: Unicode Standard Annex, UAX#9, The Unicode Bidi- A class of character has special significance in the rectional Algorithm, Version 4.1.0, [date TBD]. context of bidirectional text. The interpretation and rendering of any of these characters depend on the Unicode Standard Annex, UAX#15, Unicode Nor- state related to the symmetric swapping characters malization Forms, Version 4.1.0, [date TBD]. (see clause F.2.2) and on the direction of the char- acter being rendered that are in effect at the point in the CC-data-element where the coded representa- Page 2, Clause Terms and definitions tion of the character appears. The list of these char- Insert the following text as sub-clause 4.1 and Note; acters is provided in Annex E.1. update all following sub-clause numbers accord- NOTE – That list also represents all characters which have ingly.
    [Show full text]
  • Let the Mirrors Do the Thinking
    BRIDGES Mathematical Connections in Art, Music, and Science Let the Mirrors Do the Thinking Glenn Clark Shea Zellweger Department of Mathematics Department of Psychology Mount Union College Mount Union College Alliance, Ohio 44601 Alliance, Ohio 4460 I 1. Introduction Our story begins with a simple example. Suppose that someone asked you to keep a record of your thoughts, exactly, and in terms of the symbols given, when you are making an effort to multiply XVI times LXIV. Also suppose that, refusing to give up, you finally arrive at the right answer, which happens to be MXXIV. We are sure that you would have had a much easier time of it, to solve this problem, if you would have found that 16 times 64 equals 1024. This example not only looks at what we think and what we write. It also looks at the mental tools, the signs and symbols, that we are using when that thinking and that writing is taking place. How we got these mental tools is a long story, one that includes new developments today. What follows will run a replay of what happened when Europe took several centuries to go from MXXIV to 1024. This replay in not for numbers: it is for logic. Modem logic starts in the middle 1800s and with George Boole. This means that we have had only about 150 years to establish the symbols we now use for symbolic logic. These symbols leave a lot to be desired. We hope thatwe can draw you into taking a look at a lesson in lazy logic.
    [Show full text]