DOCSLIB.ORG

Math 1090 Part Two: Predicate (First-Order) Logic

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Math 1090 Part Two: Predicate (First-Order) Logic Math 1090 Part two: Predicate (First-Order) Logic Saeed Ghasemi York University 5th July 2018 Saeed Ghasemi (York University) Math 1090 5th July 2018 1 / 95 Question. Is propositional logic rich enough to do mathematics and computer science? The answer is \Absolutely not"! Mathematics and computer science deals with structures like sets, strings, numbers, matrices, trees, graphs, programs, Turing machines and many others. The propositional logic is not rich enough to deal with this structures. For example, try expressing the statements \there is a rational number strictly between two given rational numbers" or \every natural number has a unique prime factorization". We cannot even express these statements in the Boolean Logic, let alone proving them! Saeed Ghasemi (York University) Math 1090 5th July 2018 2 / 95 Number Theory-Peano's Arithmetic In order to express formulas in number theory: We need to be able to refer to numbers, N = f1; 2; 3;::: g as variables. we need to have variable symbols that would refer to numbers, like n; m; n0;::: . Let's call them \object variables". We need to be able to say when two numbers are equal, that's why we need a symbol \=" for the equality between the variable objects. We need to be able to say expressions like \for all natural numbers ...". So let's have a symbol 8, which says \for all". We need a special constant denoting 0. We also need to be able to add and multiply numbers. So lets have function + : N × N ! N and × : N × N ! N for addition and multiplication, respectively (we say these functions have arity2 because they take two inputs, so the function f (x; y; z) = ::: has arity 3). Saeed Ghasemi (York University) Math 1090 5th July 2018 3 / 95 Number Theory-Peano's Arithmetic We need a unary (of arity one) function S : N ! N defined by S(n) = n + 1. This is called the \successor function". Lastly we need a predicate symbol \<" expressing formulas like \2 < 3". We can abbreviate the structure obtained above by (N; 0; +; ×; S; <). We could also include = there, but since equality is going to be always part of our languages, we just presume it is there. No need to write it! But why did we need the constant 0 or the function S? Suppose we want to express 2 < 3. We need specific numbers, 2 and 3! Well, we can obtain them using 0 and S, e.g., 2 = S(S(0)) and 3 = S(S(S(0))). So we can express any specific number. Now add to the Boolean Logic our new symbols as part of the alphabet. Then we can formulate many things in our new language. For instance if we want to express n ≤ m, then we can write (n = m) _ (n < m). Saeed Ghasemi (York University) Math 1090 5th July 2018 4 / 95 The Alphabet of the General First-Order Language A language for first order logic consists of the following symbols: (I) Logical symbols 1 All of V; the Boolean Logic Alphabet. 2 Object variables: x; y; u; v; v0; v1; v2; v3; :::; x0; x1; x2; x3; ::: 3 The equality symbol: = 4 The universal quantifier symbol: 8 (II) Non-logical symbols 1 Object constants; denoted by a; b; c;::: 2 Function symbols; denoted by f ; g; h;::: 3 Predicate symbols; denoted by φ, ; φ0;::: Saeed Ghasemi (York University) Math 1090 5th July 2018 5 / 95 Note: The logical symbols belong to every first order language. However, the choice of non-logical symbols depends on the \theory" that we want to study. The equality is only for object variables (e.g., x = y) and not for Boolean variables (\≡ \does the similar job for Boolean variables). In applications, each function and predicate has a fixed arity. Each of the sets of non-logical symbols (object constants, function symbols and predicate symbols) can be empty. Examples. (1) For example the first order language for Number Theory consists of f0; +; ×; S; <g as non-logical symbols; one constant symbol 0, two binary (arity 2) functions +; ×, one unary function S and one binary predicate <. (2) The first order language for Set Theory only has one non-logical symbol, namely f2g. Saeed Ghasemi (York University) Math 1090 5th July 2018 6 / 95 Definition (Term) For a first-order language (alphabet) L a term or an L-term is defined recursively as follows: 1 Every object variable and object constant is a term. 2 If t1; t2;::: tn are terms and f is an n-ary (of arity n) function symbol (in L) then f (t1; t2;:::; tn) is also a term. The set of all terms is denoted by Term. We denote terms by 0 t; s; t ; t1;::: . Examples. In the language of Number Theory these are some terms: n 0 n + m S(S(n)) (n × m) + S(m0) Saeed Ghasemi (York University) Math 1090 5th July 2018 7 / 95 Definition (Term-Calculation/ Term-Parse) A term-calculation (or term-parse) is any finite sequence of strings that we may write respecting the following two requirements: 1 At each step we may write any object variable and object constant. 2 If t1; t2;::: tn are already written and f is an n-ary function symbol then we may write f (t1; t2;:::; tn). Proposition An string of symbols from our alphabet (language) L is a term iff it can be written in a step of a term-calculation. Saeed Ghasemi (York University) Math 1090 5th July 2018 8 / 95 Definition (Atomic formulas) For a first-order language (alphabet) L an atomic formula or an atomic L-formula is defined recursively as follows: 1 Any Boolean variable and Boolean constant is an atomic formula. 2 If t; s are terms then t = s is an atomic formula. 3 For any predicate symbol φ (in L) of arity n, and any n terms t1; t2;:::; tn the string φ(t1; t2;:::; tn) is an atomic formula. We denote the set of all atomic formulas by AF . For example m + s(0) < n × 3 and 1 + 0 = 1 are atomic formulas in the language of Number theory. Saeed Ghasemi (York University) Math 1090 5th July 2018 9 / 95 First-Order Formulas Definition (First-Order Formulas) For a first-order language (alphabet) L a formula or an L-formula is defined recursively as follows: 1 Any atomic formula is a formula. 2 If A is a formula, then (:A) is a formula. 3 If A and B are formulas, then so are (A ^ B), (A _ B),(A ! B) and (A ≡ B). 4 If A is a formula, then for any choice of (object) variable x the string ((8x)A) is a formula. Note: The sub-formula A in the formula ((8x)A) is called the scope of (8x). Note: We are only allowed to quantify over first-order (object) variables. We can not quantify over functions or predicates. For example in a first order language we are not allowed to say \for all functions f ...". Saeed Ghasemi (York University) Math 1090 5th July 2018 10 / 95 Definition (Formula-Calculation/ Formula-Parse) A formula-calculation (or formula-parse) is any finite sequence of strings that we may write respecting the following four requirements: 1 At each step we may write any atomic formula. 2 At any step we may write (:A), given that A is already written. 3 At any step we may write (A ^ B), (A _ B), (A ! B) and (A ≡ B), given that A and B are already written. 4 At any step, and for any variable x, we may write the string ((8x)A), given that we have already written A. Proposition An string of symbols from our alphabet (language) L is a formula iff it can be written in a step of a formula calculation. Saeed Ghasemi (York University) Math 1090 5th July 2018 11 / 95 Examples of formula-calculation These are some formula-calculations: p; q; ?; (p _ q); ((p _ q) !?) >; (:>); p; ?; ((:>) ^ p); q; (q _?); ((:>) ^ p) ≡ (q _?) p; x = c; ((8y)p); u = v; (:x = c); (((8y)p)_u = v); (:x = c) ! (((8y)p)_u = v) Therefore any string appearing in each of these sequences is a formula. We sometimes use the same notations WFF, to denote the set of all first -ordered (well-formed) formulas. We simply say WFF is the set of all formulas and denote its members by wff. Saeed Ghasemi (York University) Math 1090 5th July 2018 12 / 95 Definition (The Complexity of Formulas) The complexity of a wff is the total number of occurrences of 8; :; ^; _; !; ≡, in the formula. For example, p and x = y have complexity 0. ((8x)((8y)(:x = z))) has complexity 3. Definition We introduce a new symbol in the metatheory (an abbreviation, not a formal symbol) 9, called the existential quantifier. For any formula A, the string (9x)A) abbreviates the formula (:(8x)(:A)). Saeed Ghasemi (York University) Math 1090 5th July 2018 13 / 95 Priorities and Bracket Reductions 1 Outermost brackets are redundant. 2 The priorities, decreasing from left to right, is agreed to be: ((8x) and : have equal priorites.) n o (8x) : ; ^; _; !; ≡ 3 If ◦ 2 f^; _; !; ≡} and a formula is like · · · ◦ A ◦ ::: then the right ◦ acts first. That means · · · ◦ (A ◦ ::: . ::A is short for :(:A). :(8x)A is short for :((8x)A). (8x):A is short for (8x)(:A). (8x)(8x)A is short for (8x)((8y)A). (9x)(8x)A is short for (9x)((8y)A). Saeed Ghasemi (York University) Math 1090 5th July 2018 14 / 95 More Examples of Formulas Instead of (u = v ! (((8x)x = a) ^ p)) we write u = v ! (8x)x = a ^ p Instead of ((8z)(:x = y)) we write (8z):x = y Saeed Ghasemi (York University) Math 1090 5th July 2018 15 / 95 Definition (Subformulas) The concept of \B is a subformula of A" is defined inductively: 1 A is atomic: then A and B are identical strings.
Load more

Recommended publications
  • Logic and Artificial Intelligence
    Logic and Artificial Intelligence: Divorced,StillMarried,Separated...?∗ Selmer Bringsjord//David A. Ferrucci February 13, 1998 Abstract Though it’s difficult to agree on the exact date of their union, logic and artificial intelligence (AI) were married by the late 1950s, and, at least during their honeymoon, were happily united. What connubial permu- tation do logic and AI find themselves in now? Are they still (happily) married? Are they divorced? Or are they only separated, both still keep- ing alive the promise of a future in which the old magic is rekindled? This paper is an attempt to answer these questions via a review of six books. Encapsulated, our answer is that (i) logic and AI, despite tabloidish re- ports to the contrary, still enjoy matrimonial bliss, and (ii) only their future robotic offspring (as opposed to the children of connectionist AI) will mark real progress in the attempt to understand cognition. 1 The Logic–AI Marriage Though it’s difficult to agree on the exact date of their union, logic and artificial intelligence (AI) were married by the late 1950s, and, at least during their honeymoon, were happily married. But what connubial permutation do logic and AI find themselves in now? Are they still (happily) married? Are they divorced? Or are they only separated, both still keeping alive the promise of a future in which the old magic is rekindled? This paper is an attempt to answer these questions via a review of the following six books: • Ronald J. Brachman, Hector J. Levesque, and Raymond Reiter, eds., Knowledge Representation, Special Issues of Artificial Intelligence: An International Journal, Cambridge, MA: MIT Press, 1992, 408 pp., $29.00 (paper), ISBN 0-262-52168-7.
    [Show full text]
  • ERGOAI Reasoner User's Manual
    ERGOAI Reasoner User’s Manual Version 2.0 (Myia) Edited by Michael Kifer Coherent Knowledge October 2018 Portions Copyright © 2013–2018 Coherent Knowledge CONTENTS Contents 1 Introduction 1 2 Installation 1 3 Running ERGO 2 4 ERGO Shell Commands 3 5 F-logic and ERGO by Example 10 6 Main Syntactic Elements of ERGO 10 7 Basic ERGO Syntax 13 7.1 F-logic Vocabulary ..................................... 13 7.2 Symbols, Strings, and Comments ............................. 18 7.3 Operators .......................................... 21 7.4 Logical Expressions ..................................... 23 7.5 Arithmetic (and related) Expressions ........................... 23 7.6 Quasi-constants and Quasi-variables ........................... 30 7.7 Synonyms .......................................... 31 7.8 Reserved Symbols ..................................... 31 8 Path Expressions 31 9 Set Notation 33 10 Typed Variables 34 11 Truth Values and Object Values 36 12 Boolean Methods 38 Portions Copyright © 2013–2018 Coherent Knowledge i CONTENTS 12.1 Boolean Signatures ..................................... 39 13 Skolem Symbols 39 14 Testing Meta-properties of Symbols and Variables 46 15 Lists, Sets, Ranges. The Operators \in, \subset, \sublist 50 16 Multifile Knowledge Bases 51 16.1 ERGO Modules ....................................... 52 16.2 Calling Methods and Predicates Defined in User Modules ............... 53 16.3 Finding the Current Module Name ............................ 55 16.4 Finding the Module That Invoked A Rule ........................ 55 16.5 Loading Files into User Modules ............................. 55 16.6 Adding Rule Bases to Existing Modules ......................... 58 16.7 Module References in Rule Heads ............................. 59 16.8 Calling Prolog Subgoals from ERGO ........................... 60 16.9 Calling ERGO from Prolog ................................. 62 16.9.1 Importing ERGO Predicates into Prolog ..................... 62 16.9.2 Passing Arbitrary Queries to ERGO ......................
    [Show full text]
  • Cabineta Quarterly of Art and Culture
    A QUARTERLY OF ART AND CULTURE ISSUE 18 FICTIONAL STATES CABINET US $10 CANADA $15 UK £6 inside this issue THERMIDOR 2005 Sasha Archibald • John Bear • Robert Blackson • William Bryk • Sasha Chavchavadze • Mark Dery • Allen Ezell • Charles Green • Invertebrate • Craig Kalpakjian • Peter Lamborn Wilson • David Levi Strauss • Brian McMullen • Glexis Novoa • George Pendle • Elizabeth Pilliod • Patrick Pound • Bonnie and Roger Riga • Lynne Roberts-Goodwin • Tal Schori • Cecilia Sjöholm • Frances Stark • Michael Taussig • Christopher Turner • Jonathan Ward • Christine Wertheim • Tony Wood • Shea Zellweger cabinet Cabinet is a non-profit 501 (c) (3) magazine published by Immaterial Incorporated. 181 Wyckoff Street Contributions to Cabinet are fully tax-deductible. Our survival is dependent on Brooklyn NY 11217 USA such contributions; please consider supporting us at whatever level you can. tel + 1 718 222 8434 Donations of $25 or more will be acknowledged in the next possible issue. Dona- fax + 1 718 222 3700 tions above $250 will be acknowledged for four issues. Checks should be made email [email protected] out to “Cabinet.” Please mark the envelope, “Rub your eyes before opening.” www.cabinetmagazine.org Cabinet wishes to thank the following visionary foundations and individuals Summer 2005, issue 18 for their support of our activities during 2005. Additionally, we will forever be indebted to the extraordinary contribution of the Flora Family Foundation from Editor-in-chief Sina Najafi 1999 to 2004; without their generous support, this publication would not exist. Senior editor Jeffrey Kastner Thanks also to the Andy Warhol Foundation for the Visual Arts for their two-year Editors Jennifer Liese, Christopher Turner grant in 2003-2004.
    [Show full text]
  • Feature Extraction with Description Logics Functional Subsumption
    Functional Subsumption in Feature Description Logic Rodrigo de Salvo Braz1 and Dan Roth2 1 [email protected] 2 [email protected] Department of Computer Science University of Illinois at Urbana-Champaign 201 N. Goodwin Urbana, IL 61801-2302 Summary. Most machine learning algorithms rely on examples represented propo- sitionally as feature vectors. However, most data in real applications is structured and better described by sets of objects with attributes and relations between them. Typically, ad-hoc methods have been used to convert such data to feature vectors, taking, in many cases, a significant amount of the computation. Propositionaliza- tion becomes more principled if generating features from structured data is done using a formal, domain independent language that describes feature types to be extracted. This language must have limited expressivity in order to be useful while some inference procedures on it are still tractable. In this chapter we present Feature Description Logic (FDL), proposed by Cumby & Roth, where feature extraction is viewed as an inference process (subsumption). We also present an extension to FDL we call Functional FDL. FDL is ultimately based on the unification of object attributes and relations between objects in or- der to detect feature types in examples. Functional subsumption provides further abstraction by using unification modulo a Boolean function representing similar- ity between attributes and relations. This greatly improves flexibility in practical situations by accomodating variations in attributes values and relation names, in- corporating background knowledge (e.g., typos, number and gender, synomyms etc). We define the semantics of Functional subsumption and how to adapt the regular subsumption algorithm for implementing it.
    [Show full text]
  • Let the Mirrors Do the Thinking
    BRIDGES Mathematical Connections in Art, Music, and Science Let the Mirrors Do the Thinking Glenn Clark Shea Zellweger Department of Mathematics Department of Psychology Mount Union College Mount Union College Alliance, Ohio 44601 Alliance, Ohio 4460 I 1. Introduction Our story begins with a simple example. Suppose that someone asked you to keep a record of your thoughts, exactly, and in terms of the symbols given, when you are making an effort to multiply XVI times LXIV. Also suppose that, refusing to give up, you finally arrive at the right answer, which happens to be MXXIV. We are sure that you would have had a much easier time of it, to solve this problem, if you would have found that 16 times 64 equals 1024. This example not only looks at what we think and what we write. It also looks at the mental tools, the signs and symbols, that we are using when that thinking and that writing is taking place. How we got these mental tools is a long story, one that includes new developments today. What follows will run a replay of what happened when Europe took several centuries to go from MXXIV to 1024. This replay in not for numbers: it is for logic. Modem logic starts in the middle 1800s and with George Boole. This means that we have had only about 150 years to establish the symbols we now use for symbolic logic. These symbols leave a lot to be desired. We hope thatwe can draw you into taking a look at a lesson in lazy logic.
    [Show full text]
  • Elaborating a Declaration on Combating Anti-Otherness
    Alternative view of segmented documents via Kairos 20 July 2018 | Draft Elaborating a Declaration on Combating Anti-otherness including anti-science, anti-spiritual, anti-women, anti-gay, anti-socialism, anti- animal, and anti-negativity -- / -- Introduction Questionable instances of anti-otherness Draft Declaration on Combating Anti-otherness Anti-otherness, anti-alterity, anti-diversity and anti-consensus? Disputatious otherness and negative capability? Oppositional logic? Requirement for a paradoxical "anti-language"? Hyperreality and anti-otherness? Transformable architecture of future cognitive pantheons? Confusion of otherness through cognitive bias Periodic engendering of distinctive otherness Oppositional logic as comprehensible key to sustainable democracy References Introduction The following Declaration is inspired by the remarkable London Declaration on Combating Antisemitism (2009) approved at the Inter- parliamentary Coalition for Combating Antisemitism (ICCA). That initiative has been successfully followed by the articulation of a clarification of the nature of antisemitism by the European Commission (Combating Antisemitism, 6 July 2018) explicitly noting the legally non-binding working definition of antisemitism adopted unanimously by the International Holocaust Remembrance Alliance (May 2016). The clarification takes the form of a Resolution on Combating Antisemitism, as adopted by the European Parliament (1 June 2017). The question is currently the focus of considerable controversy regarding antisemitism within the UK Labour Party, as variously noted (Labour MPs back antisemitism measures rejected by Corbyn, The Guardian, 10 May 2018; Labour MP labels Corbyn an 'antisemite' over party's refusal to drop code, The Guardian, 17 July 2018; Jeremy Corbyn's anti-Semitism problem, The Economist, 31 March 2018; How should antisemitism be defined? The Guardian, 27 July 2018; Yes, Jews are angry -- because Labour hasn't listened or shown any empathy, The Guardian, 27 July 2018).
    [Show full text]
  • Logic Made Easy: How to Know When Language Deceives
    LOGIC MADE EASY ALSO BY DEBORAH J. BENNETT Randomness LOGIC MADE EASY How to Know When Language Deceives You DEBORAH J.BENNETT W • W • NORTON & COMPANY I ^ I NEW YORK LONDON Copyright © 2004 by Deborah J. Bennett All rights reserved Printed in the United States of America First Edition For information about permission to reproduce selections from this book, write to Permissions, WW Norton & Company, Inc., 500 Fifth Avenue, New York, NY 10110 Manufacturing by The Haddon Craftsmen, Inc. Book design by Margaret M.Wagner Production manager: Julia Druskin Library of Congress Cataloging-in-Publication Data Bennett, Deborah J., 1950- Logic made easy : how to know when language deceives you / Deborah J. Bennett.— 1st ed. p. cm. Includes bibliographical references and index. ISBN 0-393-05748-8 1. Reasoning. 2. Language and logic. I.Title. BC177 .B42 2004 160—dc22 2003026910 WW Norton & Company, Inc., 500 Fifth Avenue, New York, N.Y. 10110 www. wwnor ton. com WW Norton & Company Ltd., Castle House, 75/76Wells Street, LondonWlT 3QT 1234567890 CONTENTS INTRODUCTION: LOGIC IS RARE I 1 The mistakes we make l 3 Logic should be everywhere 1 8 How history can help 19 1 PROOF 29 Consistency is all I ask 29 Proof by contradiction 33 Disproof 3 6 I ALL 40 All S are P 42 Vice Versa 42 Familiarity—help or hindrance? 41 Clarity or brevity? 50 7 8 CONTENTS 3 A NOT TANGLES EVERYTHING UP 53 The trouble with not 54 Scope of the negative 5 8 A and E propositions s 9 When no means yes—the "negative pregnant" and double negative 61 k SOME Is PART OR ALL OF ALL 64 Some
    [Show full text]
  • Ideas in Action: Proceedings of the Applying Peirce Conference
    IDEAS IN ACTION Proceedings of the Applying Peirce Conference Edited by: Mats Bergman, Sami Paavola, Ahti-Veikko Pietarinen, Henrik Rydenfelt Nordic NSP Studies in Pragmatism 1 IDEAS IN ACTION Nordic Studies in Pragmatism Series editors: Mats Bergman Henrik Rydenfelt The purpose of the series is to publish high-quality monographs and col- lections of articles on the tradition of philosophical pragmatism and closely related topics. It is published online in an open access format by the Nordic Pragmatism Network, making the volumes easily accessible for scholars and students anywhere in the world. IDEAS IN ACTION PROCEEDINGS OF THE APPLYING PEIRCE CONFERENCE Nordic Studies in Pragmatism 1 Edited by Mats Bergman, Sami Paavola, Ahti-Veikko Pietarinen & Henrik Rydenfelt Nordic Pragmatism Network, NPN Helsinki 2010 Copyright c 2010 The Authors and the Nordic Pragmatism Network. This work is licensed under a Creative Commons Attribution-NonCommercial 3.0 Unported License. CC BY NC For more information, see http://creativecommons.org/licenses/by-nc/./ www.nordprag.org ISSN-L - ISSN - ISBN ---- This work is typeset with Donald Knuth’s TEX program, using LATEX2ε macros and the ‘Nnpbook’ class definition. Contents Preface iv Note on References v 1 Reconsidering Peirce’s Relevance 1 Nathan Houser Part I 2 Serving Two Masters: Peirce on Pure Science, Useless Things, and Practical Applications 17 Mats Bergman 3 The Function of Error in Knowledge and Meaning: Peirce, Apel, Davidson 38 Elizabeth F. Cooke 4 Peircean Modal Realism? 48 Sami Pihlstr¨om 5 Toward a Transcendental Pragmatic Reconciliation of Analytic and Continental Philosophy 62 Jerold J. Abrams 6 Reflections on Practical Otherness: Peirce and Applied Sciences 74 Ivo Assad Ibri 7 Problems in Applying Peirce in Social Sciences 86 Erkki Kilpinen 8 Peirce and Pragmatist Democratic Theory 105 Robert B.
    [Show full text]
  • Comprehension of Requisite Variety Via Rotation of the Complex Plane Mutually Orthogonal Renderings of the Mandelbrot Set Framing an Eightfold Way -- /
    Alternative view of segmented documents via Kairos 15 July 2019 | Draft Comprehension of Requisite Variety via Rotation of the Complex Plane Mutually orthogonal renderings of the Mandelbrot set framing an eightfold way -- / -- Introduction Mandelbrot sets rendered in a mutually orthogonal configuration of 3 complex planes Psychosocial and strategic implications of distinct octants Reframing an eightfold way by entangling imagination and reality? Comprehension of coherence currently constrained by convention Memorability: "comprehension tables" as complement to "truth tables" Metaphors associated with trigram and tetragram encodings Confrontation of highly "incompatible" frameworks as a vital necessity in times of chaos? Coherence of a cognitive nexus comprehended dynamically Fractal comprehension of coherence requiring an 8-fold uncertainty principle? References Introduction Faced with global crises, it is useful to recall the variants of the well-known insight: There Is Always a Well-Known Solution to Every Human Problem -- Neat, Plausible, and Wrong. How many of the advocated global strategies can be recognized in that light? There is no lack of recognition of the complexity of "strategic space" within which the articulation and display of strategies could be compared metaphorically to the competitive challenge faced by flowers (Keith Critchlow, The Hidden Geometry of Flowers: living rhythms, form and number, 2011). Missing is any sense of the requisite complexity within which otherwise incommensurable strategies may need to be embedded in order for their collective coherence to become comprehensible. The tendency to organize any such articulation into multiple sections -- multi-petalled "strategic flowers" -- can then be compared with the branching 3-fold, 5-fold, N-fold patterns in the animations presented separately (Dynamics of tank comprehension and enclosure, 2019).
    [Show full text]
  • Вбдгжеиз © ! #"%$ !'&)(102 #34(6587#9@'A
    ¢¡¤£¦¥¨§ © !"$#&%'()* ,+"#-% ./##&!¢01 2034'5'5#- %#&.6!¢01* 798;:=<?> @BAC>9DFE(AHG I 8KJ@L89MN@LOQPECR SUTWV¦XY:[Z @ V]\C@CO^@H_M`@H:YXba Abstract The problems of Boolean satisfiability (SAT) and automatic test pattern gen- eration (ATPG) are strongly related - both in terms of application areas (pre- manufacturing design validation and post-manufacturing testing), as well as in terms of techniques used in their practical solutions (searching large combina- torial spaces through efficient pruning). However, historically these domains have evolved somewhat independently with limited interaction. While ATPG has been primarily driven by reasoning based on circuit structure, SAT has fo- cussed on reasoning using conjunctive normal form (CNF) representations of Boolean formulas. In this chapter, we introduce these problems, describe key techniques used to solve them in practice, and highlight the common themes and differences between them. c¦dfe^c gihjlk`monqprsj¢gtmoh The problems of Boolean satisfiability (SAT) and automatic test pattern generation (ATPG) have been investigated intensively for many decades. Bool- ean satisfiability serves as an important reference problem in complexity theory of Computer Science. It has been shown that many difficult decision problems from various application domains can be reduced to the Boolean satisfiabil- ity problem. Algorithms for solving this problem have been an active field of research and steady progress has been achieved over many years. The problem of ATPG for combinational circuits is closely related to Bool- ean satisfiability. ATPG deals with the problem of efficiently generating test stimuli for testing chips after fabrication. As with SAT, ATPG has also been well studied. uwvwx u yUv z¦{}|5~WB ¤ w~]-B]~B~CL~W{B SAT and ATPG algorithms have received even stronger interest more re- cently, since they have been used successfully as Boolean engines for equiv- alence checking (see Chapter 13) and logic synthesis (see Chapter 2).
    [Show full text]
  • Symmetry and the Crystallography of Logic Shea Zellweger Mount Union College 1988 Alliance, Ohio 44601 U.S.A
    Symmetry and the Crystallography of Logic Shea Zellweger Mount Union College 1988 Alliance, Ohio 44601 U.S.A. The history of logic has been divided into three periods. The "traditional" period starts with Aristotle. The "algebraic" period starts with Boole. The "logistic" period starts when Russell successfully rescues the ideas of Frege. In what fol- lows I will be going back to the middle period, back to the time of Boole, Schroeder, and Peirce. More specifically, what follows will focus on a direct contin- uation of two of the main ideas that were emphasized by Peirce. In reference to logic, especially to what is called the proposi- tional calculus, he understood the importance of s~m~etry. In reference to notation, he understood the importance of iconicity. But he did not go far enough. What follows will show that, when we start with a custom-designed notation, it is an easy step to go from symmetry-iconicity to the crystallography of ~. In 1902 Peirce devised three iconic notations for the 16 binary connectives (and,-or, if, etc.). Before we push his work a small notch ahead, let us look at a simple example in binary logic. It expresses the duality of "and" and "or," as in |1) and (2). A mental grasp of (i) and (2} can be maintained in three ways. Mem- (i) (A and B) ~ Not(Not-A or Not-B) (2) (A . B) ~ N(NA v NB) (3) N(A . B) ~ (NAv NB) (4) N(A v B) ~ (NA . NB) orize it, derive it from something else that has been memorized, such as we see in De Morgan’s laws [(3) and (4)], or work it out again and again, each time coming back to the truth table method.
    [Show full text]
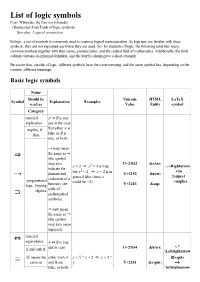
  • List of Logic Symbols ⇒ → ⊃
    List of logic symbols From Wikipedia, the free encyclopedia (Redirected from Table of logic symbols) See also: Logical connective In logic, a set of symbols is commonly used to express logical representation. As logicians are familiar with these symbols, they are not explained each time they are used. So, for students of logic, the following table lists many common symbols together with their name, pronunciation, and the related field of mathematics. Additionally, the third column contains an informal definition, and the fourth column gives a short example. Be aware that, outside of logic, different symbols have the same meaning, and the same symbol has, depending on the context, different meanings. Basic logic symbols Name Should be Unicode HTML LaTeX Symbol Explanation Examples read as Value Entity symbol Category material A ⇒ B is true implication just in the case implies; if .. that either A is then false or B is true, or both. → may mean the same as ⇒ ⇒ (the symbol may also U+21D2 &rArr; x = 2 ⇒ x2 = 4 is true, \Rightarrow indicate the 2 \to domain and but x = 4 ⇒ x = 2 is in U+2192 &rarr; → \supset codomain of a general false (since x propositional could be −2). \implies logic, Heyting function; see U+2283 &sup; algebra table of ⊃ mathematical symbols). ⊃ may mean the same as ⇒ (the symbol may also mean superset). material ⇔ equivalence A ⇔ B is true if and only if; just in case U+21D4 &hArr; \Leftrightarrow iff; means the either both A x + 5 = y + 2 ⇔ x + 3 = \equiv ≡ same as and B are y U+2261 &equiv; false, or both \leftrightarrow false, or both \leftrightarrow propositional A and B are U+2194 &harr; \iff true.
    [Show full text]