A Simple Demonstration of Frustrated Total Internal Reflection
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Model and Visualization of Ray Tracing Using Javascript and HTML5 for TIR Measurement System Equipped with Equilateral Right Angle Prism
Invited talk in parallel session of the 2nd Indonesian Student Conference on Science and Mathematics (ISCSM-2), 11-12 October 2013, Bandung, Indonesia Model and Visualization of Ray Tracing using JavaScript and HTML5 for TIR Measurement System Equipped with Equilateral Right Angle Prism S. Viridi 1 and Hendro 2 1Nuclear Physics and Biophysics, Institut Teknologi Bandung, Bandung 40132, Indonesia 2Theoretical High Energy Physics and Instrumentation, Institut Teknologi Bandung, Bandung 40132, Indonesia [email protected], [email protected] Abstract Trace of ray deviated by a prism, which is common in a TIR (total internal reflection) 2013 measurement system, is sometimes difficult to manage, especially if the prism is an Oct equilateral right angle prism (ERAP). The point where the ray is reflected inside the right- 2 1 angle prism is also changed as the angle of incident ray changed. In an ATR (attenuated total reflectance) measurement system, range of this point determines size of sample. Using JavaScript and HTML5 model and visualization of ray tracing deviated by an ERAP is perform and reported in this work. Some data are obtained from this visualization and an empirical relations between angle of incident ray source θS , angle of ray detector hand θ D′ , [physics.optics] and angle of ray detector θ D are presented for radial position of ray source RS = 25 cm , v1 radial position of ray detector RD = 20 cm , height of right-angle prism t =15 cm , and 0000 . 0 refractive index of the prism n = 5.1 . 1 Keywords: deviation angle, equilateral right angle prism, total internal reflection, JavaScript, HTML5. -

Bringing Optical Metamaterials to Reality
UC Berkeley UC Berkeley Electronic Theses and Dissertations Title Bringing Optical Metamaterials to Reality Permalink https://escholarship.org/uc/item/5d37803w Author Valentine, Jason Gage Publication Date 2010 Peer reviewed|Thesis/dissertation eScholarship.org Powered by the California Digital Library University of California Bringing Optical Metamaterials to Reality By Jason Gage Valentine A dissertation in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Engineering – Mechanical Engineering in the Graduate Division of the University of California, Berkeley Committee in charge: Professor Xiang Zhang, Chair Professor Costas Grigoropoulos Professor Liwei Lin Professor Ming Wu Fall 2010 Bringing Optical Metamaterials to Reality © 2010 By Jason Gage Valentine Abstract Bringing Optical Metamaterials to Reality by Jason Gage Valentine Doctor of Philosophy in Mechanical Engineering University of California, Berkeley Professor Xiang Zhang, Chair Metamaterials, which are artificially engineered composites, have been shown to exhibit electromagnetic properties not attainable with naturally occurring materials. The use of such materials has been proposed for numerous applications including sub-diffraction limit imaging and electromagnetic cloaking. While these materials were first developed to work at microwave frequencies, scaling them to optical wavelengths has involved both fundamental and engineering challenges. Among these challenges, optical metamaterials tend to absorb a large amount of the incident light and furthermore, achieving devices with such materials has been difficult due to fabrication constraints associated with their nanoscale architectures. The objective of this dissertation is to describe the progress that I have made in overcoming these challenges in achieving low loss optical metamaterials and associated devices. The first part of the dissertation details the development of the first bulk optical metamaterial with a negative index of refraction. -

Introduction to the Ray Optics Module
INTRODUCTION TO Ray Optics Module Introduction to the Ray Optics Module © 1998–2020 COMSOL Protected by patents listed on www.comsol.com/patents, and U.S. Patents 7,519,518; 7,596,474; 7,623,991; 8,457,932; 9,098,106; 9,146,652; 9,323,503; 9,372,673; 9,454,625; 10,019,544; 10,650,177; and 10,776,541. Patents pending. This Documentation and the Programs described herein are furnished under the COMSOL Software License Agreement (www.comsol.com/comsol-license-agreement) and may be used or copied only under the terms of the license agreement. COMSOL, the COMSOL logo, COMSOL Multiphysics, COMSOL Desktop, COMSOL Compiler, COMSOL Server, and LiveLink are either registered trademarks or trademarks of COMSOL AB. All other trademarks are the property of their respective owners, and COMSOL AB and its subsidiaries and products are not affiliated with, endorsed by, sponsored by, or supported by those trademark owners. For a list of such trademark owners, see www.comsol.com/ trademarks. Version: COMSOL 5.6 Contact Information Visit the Contact COMSOL page at www.comsol.com/contact to submit general inquiries, contact Technical Support, or search for an address and phone number. You can also visit the Worldwide Sales Offices page at www.comsol.com/contact/offices for address and contact information. If you need to contact Support, an online request form is located at the COMSOL Access page at www.comsol.com/support/case. Other useful links include: • Support Center: www.comsol.com/support • Product Download: www.comsol.com/product-download • Product Updates: www.comsol.com/support/updates •COMSOL Blog: www.comsol.com/blogs • Discussion Forum: www.comsol.com/community •Events: www.comsol.com/events • COMSOL Video Gallery: www.comsol.com/video • Support Knowledge Base: www.comsol.com/support/knowledgebase Part number. -

Section 22-3: Energy, Momentum and Radiation Pressure
Answer to Essential Question 22.2: (a) To find the wavelength, we can combine the equation with the fact that the speed of light in air is 3.00 " 108 m/s. Thus, a frequency of 1 " 1018 Hz corresponds to a wavelength of 3 " 10-10 m, while a frequency of 90.9 MHz corresponds to a wavelength of 3.30 m. (b) Using Equation 22.2, with c = 3.00 " 108 m/s, gives an amplitude of . 22-3 Energy, Momentum and Radiation Pressure All waves carry energy, and electromagnetic waves are no exception. We often characterize the energy carried by a wave in terms of its intensity, which is the power per unit area. At a particular point in space that the wave is moving past, the intensity varies as the electric and magnetic fields at the point oscillate. It is generally most useful to focus on the average intensity, which is given by: . (Eq. 22.3: The average intensity in an EM wave) Note that Equations 22.2 and 22.3 can be combined, so the average intensity can be calculated using only the amplitude of the electric field or only the amplitude of the magnetic field. Momentum and radiation pressure As we will discuss later in the book, there is no mass associated with light, or with any EM wave. Despite this, an electromagnetic wave carries momentum. The momentum of an EM wave is the energy carried by the wave divided by the speed of light. If an EM wave is absorbed by an object, or it reflects from an object, the wave will transfer momentum to the object. -
Properties of Electromagnetic Waves Any Electromagnetic Wave Must Satisfy Four Basic Conditions: 1
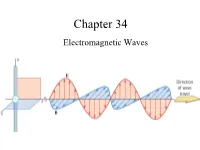
Chapter 34 Electromagnetic Waves The Goal of the Entire Course Maxwell’s Equations: Maxwell’s Equations James Clerk Maxwell •1831 – 1879 •Scottish theoretical physicist •Developed the electromagnetic theory of light •His successful interpretation of the electromagnetic field resulted in the field equations that bear his name. •Also developed and explained – Kinetic theory of gases – Nature of Saturn’s rings – Color vision Start at 12:50 https://www.learner.org/vod/vod_window.html?pid=604 Correcting Ampere’s Law Two surfaces S1 and S2 near the plate of a capacitor are bounded by the same path P. Ampere’s Law states that But it is zero on S2 since there is no conduction current through it. This is a contradiction. Maxwell fixed it by introducing the displacement current: Fig. 34-1, p. 984 Maxwell hypothesized that a changing electric field creates an induced magnetic field. Induced Fields . An increasing solenoid current causes an increasing magnetic field, which induces a circular electric field. An increasing capacitor charge causes an increasing electric field, which induces a circular magnetic field. Slide 34-50 Displacement Current d d(EA)d(q / ε) 1 dq E 0 dt dt dt ε0 dt dq d ε E dt0 dt The displacement current is equal to the conduction current!!! Bsd μ I μ ε I o o o d Maxwell’s Equations The First Unified Field Theory In his unified theory of electromagnetism, Maxwell showed that electromagnetic waves are a natural consequence of the fundamental laws expressed in these four equations: q EABAdd 0 εo dd Edd s BE B s μ I μ ε dto o o dt QuickCheck 34.4 The electric field is increasing. -

Lecture 26 – Propagation of Light Spring 2013 Semester Matthew Jones Midterm Exam
Physics 42200 Waves & Oscillations Lecture 26 – Propagation of Light Spring 2013 Semester Matthew Jones Midterm Exam Almost all grades have been uploaded to http://chip.physics.purdue.edu/public/422/spring2013/ These grades have not been adjusted Exam questions and solutions are available on the Physics 42200 web page . Outline for the rest of the course • Polarization • Geometric Optics • Interference • Diffraction • Review Polarization by Partial Reflection • Continuity conditions for Maxwell’s Equations at the boundary between two materials • Different conditions for the components of or parallel or perpendicular to the surface. Polarization by Partial Reflection • Continuity of electric and magnetic fields were different depending on their orientation: – Perpendicular to surface = = – Parallel to surface = = perpendicular to − cos + cos − cos = cos + cos cos = • Solve for /: − = !" + !" • Solve for /: !" = !" + !" perpendicular to cos − cos cos = cos + cos cos = • Solve for /: − = !" + !" • Solve for /: !" = !" + !" Fresnel’s Equations • In most dielectric media, = and therefore # sin = = = = # sin • After some trigonometry… sin − tan − = − = sin + tan + ) , /, /01 2 ) 45/ 2 /01 2 * = - . + * = + * )+ /01 2+32* )+ /01 2+32* 45/ 2+62* For perpendicular and parallel to plane of incidence. Application of Fresnel’s Equations • Unpolarized light in air ( # = 1) is incident -

Surface Plasmon Enhanced Evanescent Wave Laser Linac
Particle Accelerators, 1993, Vol. 40, pp.171-179 © 1993 Gordon & Breach Science Publishers, S.A. Reprints available directly from the publisher Printed in the United States of America. Photocopying permitted by license only SURFACE PLASMON ENHANCED EVANESCENT WAVE LASER LINAC T. H. KOSCHMIEDER* Department ofPhysicsIRLM5.208, University ofTexas at Austin, Austin, TX 78712 (Received 17 January 1992; in final form 25 September 1992) The grating laser linac concept of Palmer will be modified to incorporate a surface plasmon excitation in the visible part of the optical spectrum. Both grating and prism coupling of light to the surface plasmon will be discussed. It will be shown that phase matching between a relativistic particle and the surface plasmon can be achieved. Finally calculations will be presented showing that accelerations up to 14 GeV1m for a grating and up to 7 GeV1m for a prism could be obtained for incident power densities less than a nominal damage threshold. KEY WORDS: Laser-beam accelerators, Surface plasmons INTRODUCTION There is an ongoing interest in increasing the exit energy of particles from linacs. One possibility of achieving this is by PalmerI who showed that light incident upon a grating ? at skew angles could achieve very high accelerations (GeV1m). The relativistic particles travel just above the grating and are accelerated by coupling to evanescent waves. One effect that can occur for light incident upon a metal grating is the excitation of 2 a surface plasmon. Surface plasmon excitationc in the visible part of the spectrum will be explored in this paper. It will be shown that surface plasmon excitation in the visible part of the spectrum can be used to accelerate relativistic particles. -

The Human Ear Hearing, Sound Intensity and Loudness Levels
UIUC Physics 406 Acoustical Physics of Music The Human Ear Hearing, Sound Intensity and Loudness Levels We’ve been discussing the generation of sounds, so now we’ll discuss the perception of sounds. Human Senses: The astounding ~ 4 billion year evolution of living organisms on this planet, from the earliest single-cell life form(s) to the present day, with our current abilities to hear / see / smell / taste / feel / etc. – all are the result of the evolutionary forces of nature associated with “survival of the fittest” – i.e. it is evolutionarily{very} beneficial for us to be able to hear/perceive the natural sounds that do exist in the environment – it helps us to locate/find food/keep from becoming food, etc., just as vision/sight enables us to perceive objects in our 3-D environment, the ability to move /locomote through the environment enhances our ability to find food/keep from becoming food; Our sense of balance, via a stereo-pair (!) of semi-circular canals (= inertial guidance system!) helps us respond to 3-D inertial forces (e.g. gravity) and maintain our balance/avoid injury, etc. Our sense of taste & smell warn us of things that are bad to eat and/or breathe… Human Perception of Sound: * The human ear responds to disturbances/temporal variations in pressure. Amazingly sensitive! It has more than 6 orders of magnitude in dynamic range of pressure sensitivity (12 orders of magnitude in sound intensity, I p2) and 3 orders of magnitude in frequency (20 Hz – 20 KHz)! * Existence of 2 ears (stereo!) greatly enhances 3-D localization of sounds, and also the determination of pitch (i.e. -

How Does Light Work? Making a Water Prism
How does light work? Making a water prism How do we see color? In this activity students release the colors in the rainbow through the action of bending light in a water prism. Time Grade Next Generation Science Standards • 5 minutes prep time • 1-4 • 1-PS4-3. Plan and conduct an investigation to determine the effect of placing objects made with different materials in the path of light. • 10 minutes class time • 4-PS4-1. Develop a model of waves to describe patterns in terms of for activity amplitude and wavelength. • More if you are using • 4– PS3-2. Make observations to provide evidence that energy can be the Lab Sheet transferred from place to place by sound, light, heat and electric currents. Materials Utah Science Core Standards You will need to do this outside or with the • K-2 Standard 2– Earth and Space Science sunlight streaming through a window • 3.1.1b Explain the sun is the source of light that lights the moon A bowl full of water A mirror A sheet of white paper Science notebook or lab sheet Directions • You may want to view this video ahead of time which shows how to move the paper to find the rainbow How to make a water prism https://www.youtube.com/watch?v=D8g4l8mSonM • You may want to introduce your class to color and light with this video Light and Color (Bill Nye) https://www.youtube.com/watch?v=dH1YH0zEAik&t=10s GBO suggestion - Do this activity as a station in a rotation with several other light activities. -

The Fresnel Equations and Brewster's Law
The Fresnel Equations and Brewster's Law Equipment Optical bench pivot, two 1 meter optical benches, green laser at 543.5 nm, 2 10cm diameter polarizers, rectangular polarizer, LX-02 photo-detector in optical mount, thick acrylic block, thick glass block, Phillips multimeter, laser mount, sunglasses. Purpose To investigate polarization by reflection. To understand and verify the Fresnel equations. To explore Brewster’s Law and find Brewster’s angle experimentally. To use Brewster’s law to find Brewster’s angle. To gain experience working with optical equipment. Theory Light is an electromagnetic wave, of which fundamental characteristics can be described in terms of the electric field intensity. For light traveling along the z-axis, this can be written as r r i(kz−ωt) E = E0e (1) r where E0 is a constant complex vector, and k and ω are the wave number and frequency respectively, with k = 2π / λ , (2) λ being the wavelength. The purpose of this lab is to explore the properties the electric field in (1) at the interface between two media with indices of refraction ni and nt . In general, there will be an incident, reflected and transmitted wave (figure 1), which in certain cases reduce to incident and reflected or incident and transmitted only. Recall that the angles of the transmitted and reflected beams are described by the law of reflection and Snell’s law. This however tells us nothing about the amplitudes of the reflected and transmitted Figure 1 electric fields. These latter properties are defined by the Fresnel equations, which we review below. -

Reflection and Refraction of Light
Reflection and refraction When light hits a surface, one or more of three things may happen. The light may be reflected back from the surface, transmitted through the material (in which case it will deviate from its initial direction, a process known as refraction) or absorbed by the material if it is not transparent at the wavelength of the incident light. 1. Reflection and refraction Reflection and refraction are governed by two very simple laws. We consider a light wave travelling through medium 1 and striking medium 2. We define the angle of incidence θ as the angle between the incident ray and the normal to the surface (a vector pointing out perpendicular to the surface). For reflection, the reflected ray lies in the plane of incidence, and θ1’ = θ1 For refraction, the refracted ray lies in the plane of incidence, and n1sinθ1 = n2sinθ2 (this expression is called Snell’s law). In the above equations, ni is a dimensionless constant known as the θ1 θ1’ index of refraction or refractive index of medium i. In addition to reflection determining the angle of refraction, n also determines the speed of the light wave in the medium, v = c/n. Just as θ1 is the angle between refraction θ2 the incident ray and the surface normal outside the medium, θ2 is the angle between the transmitted ray and the surface normal inside the medium (i.e. pointing out from the other side of the surface to the original surface normal) 2. Total internal reflection A consequence of Snell’s law is a phenomenon known as total internal reflection. -

Chapter 12: Physics of Ultrasound
Chapter 12: Physics of Ultrasound Slide set of 54 slides based on the Chapter authored by J.C. Lacefield of the IAEA publication (ISBN 978-92-0-131010-1): Diagnostic Radiology Physics: A Handbook for Teachers and Students Objective: To familiarize students with Physics or Ultrasound, commonly used in diagnostic imaging modality. Slide set prepared by E.Okuno (S. Paulo, Brazil, Institute of Physics of S. Paulo University) IAEA International Atomic Energy Agency Chapter 12. TABLE OF CONTENTS 12.1. Introduction 12.2. Ultrasonic Plane Waves 12.3. Ultrasonic Properties of Biological Tissue 12.4. Ultrasonic Transduction 12.5. Doppler Physics 12.6. Biological Effects of Ultrasound IAEA Diagnostic Radiology Physics: a Handbook for Teachers and Students – chapter 12,2 12.1. INTRODUCTION • Ultrasound is the most commonly used diagnostic imaging modality, accounting for approximately 25% of all imaging examinations performed worldwide nowadays • Ultrasound is an acoustic wave with frequencies greater than the maximum frequency audible to humans, which is 20 kHz IAEA Diagnostic Radiology Physics: a Handbook for Teachers and Students – chapter 12,3 12.1. INTRODUCTION • Diagnostic imaging is generally performed using ultrasound in the frequency range from 2 to 15 MHz • The choice of frequency is dictated by a trade-off between spatial resolution and penetration depth, since higher frequency waves can be focused more tightly but are attenuated more rapidly by tissue The information in an ultrasonic image is influenced by the physical processes underlying propagation, reflection and attenuation of ultrasound waves in tissue IAEA Diagnostic Radiology Physics: a Handbook for Teachers and Students – chapter 12,4 12.1.