Chance, Choice, and Change Or Can Random Events Follow Laws?
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Heads and Tails Unit Overview
6 Heads and tails Unit Overview Outcomes READING In this unit pupils will: Pupils can: ●● Describe wild animals. ●● recognise cognates and deduce meaning of words in ●● Ask and answer about favourite animals. context. ●● Compare different animals’ bodies. ●● understand a poem, find specific information and transfer ●● Write about a wild animal. this to a table. ●● read and complete a gapped text about two animals. Productive Language WRITING VOCABULARY Pupils can: ●● Animals: a crocodile, an elephant, a giraffe, a hippo, ●● write short descriptive texts following a model. a monkey, an ostrich, a pony, a snake. Strategies ●● Body parts: an arm, fingers, a foot, a head, a leg, a mouth, a nose, a tail, teeth, toes, wings. Listen for words that are similar in other languages. L 1 ●● Adjectives: fat, funny, hot, long, short, silly, tall. PB p.35 ex2 PHRASES Before you listen, look at the pictures and guess. ●● It has got/It hasn’t got (a long neck). L 2 AB p.39 ex5 ●● Has it got legs? Yes, it has./No, it hasn’t. Read the questions before you listen. Receptive Language L 3 PB p.39 ex1 VOCABULARY Listen and try to understand the main idea. ●● Animals: butterfly, meerkat, penguin, whale. L 4 ●● Africa, apple, beak, carrot, lake, water, wildlife park. PB p.36 ex1 ●● Eat, live, fly. S Use the model to help you speak. PHRASES 3 PB p.38 ex2 ●● It lives ... Look for words that are similar in other languages. R 2 Recycled Language AB p.38 ex1 VOCABULARY Use your Picture Dictionary to help you spell. -

Probability and Counting Rules
blu03683_ch04.qxd 09/12/2005 12:45 PM Page 171 C HAPTER 44 Probability and Counting Rules Objectives Outline After completing this chapter, you should be able to 4–1 Introduction 1 Determine sample spaces and find the probability of an event, using classical 4–2 Sample Spaces and Probability probability or empirical probability. 4–3 The Addition Rules for Probability 2 Find the probability of compound events, using the addition rules. 4–4 The Multiplication Rules and Conditional 3 Find the probability of compound events, Probability using the multiplication rules. 4–5 Counting Rules 4 Find the conditional probability of an event. 5 Find the total number of outcomes in a 4–6 Probability and Counting Rules sequence of events, using the fundamental counting rule. 4–7 Summary 6 Find the number of ways that r objects can be selected from n objects, using the permutation rule. 7 Find the number of ways that r objects can be selected from n objects without regard to order, using the combination rule. 8 Find the probability of an event, using the counting rules. 4–1 blu03683_ch04.qxd 09/12/2005 12:45 PM Page 172 172 Chapter 4 Probability and Counting Rules Statistics Would You Bet Your Life? Today Humans not only bet money when they gamble, but also bet their lives by engaging in unhealthy activities such as smoking, drinking, using drugs, and exceeding the speed limit when driving. Many people don’t care about the risks involved in these activities since they do not understand the concepts of probability. -

Klondike Solitaire Solvability
Klondike Solitaire Solvability Mikko Voima BACHELOR’S THESIS April 2021 Degree Programme in Business Information Systems Option of Game Development ABSTRACT Tampereen ammattikorkeakoulu Tampere University of Applied Sciences Degree Programme in Business Information Systems Option of Game Development VOIMA, MIKKO: Klondike Solitaire Solvability Bachelor's thesis 32 pages, of which appendices 1 page June 2021 Klondike solitaire remains one of the most popular single-player card games, but the exact odds of winning were discovered as late as 2019. The objective of this thesis was to study Klondike solitaire solvability from the game design point of view. The purpose of this thesis was to develop a solitaire prototype and use it as a testbed to study the solvability of Klondike. The theoretical section explores the card game literature and the academic studies on the solvability of Klondike solitaire. Furthermore, Klondike solitaire rule variations and the game mechanics are analysed. In the practical section a Klondike game prototype was developed using Unity game engine. A new fast recursive method was developed which can detect 2.24% of random card configurations as unsolvable without simulating any moves. The study indicates that determining the solvability of Klondike is a computationally complex NP-complete problem. Earlier studies proved empirically that approximately 82% of the card configurations are solvable. The method developed in this thesis could detect over 12% of the unsolvable card configurations without making any moves. The method can be used to narrow the search space of brute-force searches and applied to other problems. Analytical research on Klondike solvability is called for because the optimal strategy is still not known. -

Stories of the Fallen Willow
Stories of the Fallen Willow by Jessica Noel Casimir Senior Honors Thesis Department of English and Comparative Literature April 2020 1 dedication To my parents who sacrifice without hesitation to support my ambitions, To my professors who invested their time and shared their wisdom, And to my fellow-writer friends made along the way. Thank you for the unconditional support and words of encouragement. 2 table of contents Preface…………………………………………………………………………….4 Sellout……………………………………………………………………………..9 Papercuts…………………………………………………………………………24 Static……………………………………………………………………………...27 Dinosaur Bones………………………………………………………………..…32 How to Prepare for a Beach Trip in 4 Easy Steps………………………………..37 A Giver…………………………………………………………………………...39 Hereditary………………………………………………………………………...42 Tomato Soup…………………………………………………………………...…46 A Fair Trade………………………………………………………………………53 Fifth Base…………………………………………………………………………55 Remembering Bennett………………………………………………………….…60 Yellow Puddles……………………………………………………………………69 Head First…………………………………………………………………...…….71 3 preface This introduction is meant to be a moment of honesty. So, I’ll be candid in saying that this is my eighth attempt at writing it. I’ve started and stopped, deleted and retyped, closed my laptop and reopened it. Never in my life have I found it this difficult to write, never in my life has my body physically ached at the thought of sitting down and spending time in my own headspace. Right now, my headspace is the last place on earth I want to be. I’ve decided that this will be my last attempt at writing, and whatever comes out now will remain on the page. I am currently sitting on my couch under a pile of blankets, reclined back as far as my seat will allow me to go. My Amazon Alexa is belting music from an oldies playlist, and my dad is sitting at the kitchen table singing along to “December, 1963” by The Four Seasons as he works. -

Problem Set 1: Fake It 'Til You Make It
Water, water, everywhere.... Problem Set 1: Fake It ’Til You Make It Welcome to PCMI. We know you’ll learn a lot of mathematics here—maybe some new tricks, maybe some new perspectives on things with which you’re already familiar. Here’s a few things you should know about how the class is organized. • Don’t worry about answering all the questions. If you’re answering every question, we haven’t written the prob- lem sets correctly. Some problems are actually unsolved. Participants in • Don’t worry about getting to a certain problem number. this course have settled at Some participants have been known to spend the entire least one unsolved problem. session working on one problem (and perhaps a few of its extensions or consequences). • Stop and smell the roses. Getting the correct answer to a question is not a be-all and end-all in this course. How does the question relate to others you’ve encountered? How do others think about this question? • Respect everyone’s views. Remember that you have something to learn from everyone else. Remember that everyone works at a different pace. • Teach only if you have to. You may feel tempted to teach others in your group. Fight it! We don’t mean you should ignore people, but don’t step on someone else’s aha mo- ment. If you think it’s a good time to teach your col- leagues about Bayes’ Theorem, don’t: problems should lead to appropriate mathematics rather than requiring it. The same goes for technology: problems should lead to using appropriate tools rather than requiring them. -

Chapter 7 Homework Answers
118 CHAPTER 7: PROBABILITY: LIVING WITH THE ODDS 9. a. The sum of all the probabilities for a probability distribution is always 1. UNIT 7A 10. a. If Triple Treat’s probability of winning is 1/4, then the probability he loses is 3/4. This implies TIME OUT TO THINK the odds that he wins is (1/4) ÷ (3/4), or 1 to 3, Pg. 417. Birth orders of BBG, BGB, and GBB are the which, in turn, means the odds against are 3 to 1. outcomes that produce the event of two boys in a family of 3. We can represent the probability of DOES IT MAKE SENSE? two boys as P(2 boys). This problem is covered 7. Makes sense. The outcomes are HTTT, THTT, later in Example 3. TTHT, TTTH. Pg. 419. The only change from the Example 2 8. Does not make sense. The probability of any event solution is that the event of a July 4 birthday is is always between 0 and 1. only 1 of the 365 possible outcomes, so the 9. Makes sense. This is a subjective probability, but probability is 1/365. it’s as good as any other guess one might make. Pg. 421. (Should be covered only if you covered Unit 10. Does not make sense. The two outcomes in 6D). The experiment is essentially a hypothesis question are not equally likely. test. The null hypothesis is that the coins are fair, 11. Does not make sense. The sum of P(A) and P(not in which case we should observe the theoretical A) is always 1. -

HANDSOME= JOINS BELMONT; >LEE= WORKS
MONDAY, JUNE 5, 2017 >HANDSOME= JOINS WARD LAYS OUT PLANS FOR ROYAL ASCOT CONTINGENT by Bill Finley BELMONT; >LEE= WORKS Wesley Ward will put his Royal Ascot-bound horses through their final round of serious preparations Monday morning at Keeneland, where several will show up on the work tab. A few could be added or dropped from the list of his Royal Ascot runners depending on how they work, but for the most part, Ward has all his plans in line. AI am very strong in all the categories with the horses I=m coming in with,@ Ward said on this week=s TDN podcast. AI know the races now, I know what it takes to win. All the horses I am bringing are going to be very competitive.@ Who=s In: Lady Aurelia (Scat Daddy): A winner last year at Royal Ascot in the G2 Queen Mary S., the 3-year-old filly will take on males in the G1 King=s Stand S. June 20. She is coming off a win in the April 15 Giant=s Causeway S. at Keeneland. Cont. p3 Hollywood Handsome | Coady Photography IN TDN EUROPE TODAY BRAMETOT PREVAILS IN FRENCH DERBY Mark Stanley=s Hollywood Handsome (Tapizar) has been Jean Caude Rouget’s Brametot (Fr) (Rajsaman {Fr}) clinched a added to the GI Belmont S. line-up, according to trainer Dallas second Classic when winning the G1 Prix Du Jockey Club at Stewart Sunday. Chantilly. Click or tap here to go straight to TDN Europe. AI=m so excited to get this horse to the Belmont,@ Stewart said. -
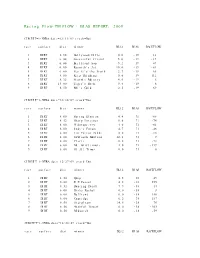
Racing Flow-TM FLOW + BIAS REPORT: 2009
Racing Flow-TM FLOW + BIAS REPORT: 2009 CIRCUIT=1-NYRA date=12/31/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 5.50 Hollywood Hills 0.0 -19 13 2 DIRT 6.00 Successful friend 5.0 -19 -19 3 DIRT 6.00 Brilliant Son 5.2 -19 47 4 DIRT 6.00 Raynick's Jet 10.6 -19 -61 5 DIRT 6.00 Yes It's the Truth 2.7 -19 65 6 DIRT 8.00 Keep Thinking 0.0 -19 -112 7 DIRT 8.32 Storm's Majesty 4.0 -19 6 8 DIRT 13.00 Tiger's Rock 9.4 -19 6 9 DIRT 8.50 Mel's Gold 2.5 -19 69 CIRCUIT=1-NYRA date=12/30/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 8.00 Spring Elusion 4.4 71 -68 2 DIRT 8.32 Sharp Instinct 0.0 71 -74 3 DIRT 6.00 O'Sotopretty 4.0 71 -61 4 DIRT 6.00 Indy's Forum 4.7 71 -46 5 DIRT 6.00 Ten Carrot Nikki 0.0 71 -18 6 DIRT 8.00 Sawtooth Moutain 12.1 71 9 7 DIRT 6.00 Cleric 0.6 71 -73 8 DIRT 6.00 Mt. Glittermore 4.0 71 -119 9 DIRT 6.00 Of All Times 0.0 71 0 CIRCUIT=1-NYRA date=12/27/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 8.50 Quip 4.5 -38 49 2 DIRT 6.00 E Z Passer 4.2 -38 255 3 DIRT 8.32 Dancing Daisy 7.9 -38 14 4 DIRT 6.00 Risky Rachel 0.0 -38 8 5 DIRT 6.00 Kaffiend 0.0 -38 150 6 DIRT 6.00 Capridge 6.2 -38 187 7 DIRT 8.50 Stargleam 14.5 -38 76 8 DIRT 8.50 Wishful Tomcat 0.0 -38 -203 9 DIRT 8.50 Midwatch 0.0 -38 -59 CIRCUIT=1-NYRA date=12/26/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 6.00 Papaleo 7.0 108 129 2 DIRT 6.00 Overcommunication 1.0 108 -72 3 DIRT 6.00 Digger 0.0 108 -211 4 DIRT 6.00 Bryan Kicks 0.0 108 136 5 DIRT 6.00 We Get It 16.8 108 129 6 DIRT 6.00 Yawanna Trust 4.5 108 -21 7 DIRT 6.00 Smarty Karakorum 6.5 108 83 8 DIRT 8.32 Almighty Silver 18.7 108 133 9 DIRT 8.32 Offlee Cool 0.0 108 -60 CIRCUIT=1-NYRA date=12/13/09 track=Dot race surface dist winner BL12 BIAS RACEFLOW 1 DIRT 8.32 Crafty Bear 3.0 -158 -139 2 DIRT 6.00 Cheers Darling 0.5 -158 61 3 DIRT 6.00 Iberian Gate 3.0 -158 154 4 DIRT 6.00 Pewter 0.5 -158 8 5 DIRT 6.00 Wolfson 6.2 -158 86 6 DIRT 6.00 Mr. -

\0-9\0 and X ... \0-9\0 Grad Nord ... \0-9\0013 ... \0-9\007 Car Chase ... \0-9\1 X 1 Kampf ... \0-9\1, 2, 3
... \0-9\0 and X ... \0-9\0 Grad Nord ... \0-9\0013 ... \0-9\007 Car Chase ... \0-9\1 x 1 Kampf ... \0-9\1, 2, 3 ... \0-9\1,000,000 ... \0-9\10 Pin ... \0-9\10... Knockout! ... \0-9\100 Meter Dash ... \0-9\100 Mile Race ... \0-9\100,000 Pyramid, The ... \0-9\1000 Miglia Volume I - 1927-1933 ... \0-9\1000 Miler ... \0-9\1000 Miler v2.0 ... \0-9\1000 Miles ... \0-9\10000 Meters ... \0-9\10-Pin Bowling ... \0-9\10th Frame_001 ... \0-9\10th Frame_002 ... \0-9\1-3-5-7 ... \0-9\14-15 Puzzle, The ... \0-9\15 Pietnastka ... \0-9\15 Solitaire ... \0-9\15-Puzzle, The ... \0-9\17 und 04 ... \0-9\17 und 4 ... \0-9\17+4_001 ... \0-9\17+4_002 ... \0-9\17+4_003 ... \0-9\17+4_004 ... \0-9\1789 ... \0-9\18 Uhren ... \0-9\180 ... \0-9\19 Part One - Boot Camp ... \0-9\1942_001 ... \0-9\1942_002 ... \0-9\1942_003 ... \0-9\1943 - One Year After ... \0-9\1943 - The Battle of Midway ... \0-9\1944 ... \0-9\1948 ... \0-9\1985 ... \0-9\1985 - The Day After ... \0-9\1991 World Cup Knockout, The ... \0-9\1994 - Ten Years After ... \0-9\1st Division Manager ... \0-9\2 Worms War ... \0-9\20 Tons ... \0-9\20.000 Meilen unter dem Meer ... \0-9\2001 ... \0-9\2010 ... \0-9\21 ... \0-9\2112 - The Battle for Planet Earth ... \0-9\221B Baker Street ... \0-9\23 Matches .. -

Name of Game Date of Approval Comments Nevada Gaming Commission Approved Gambling Games Effective August 1, 2021
NEVADA GAMING COMMISSION APPROVED GAMBLING GAMES EFFECTIVE AUGUST 1, 2021 NAME OF GAME DATE OF APPROVAL COMMENTS 1 – 2 PAI GOW POKER 11/27/2007 (V OF PAI GOW POKER) 1 BET THREAT TEXAS HOLD'EM 9/25/2014 NEW GAME 1 OFF TIE BACCARAT 10/9/2018 2 – 5 – 7 POKER 4/7/2009 (V OF 3 – 5 – 7 POKER) 2 CARD POKER 11/19/2015 NEW GAME 2 CARD POKER - VERSION 2 2/2/2016 2 FACE BLACKJACK 10/18/2012 NEW GAME 2 FISTED POKER 21 5/1/2009 (V OF BLACKJACK) 2 TIGERS SUPER BONUS TIE BET 4/10/2012 (V OF BACCARAT) 2 WAY WINNER 1/27/2011 NEW GAME 2 WAY WINNER - COMMUNITY BONUS 6/6/2011 21 + 3 CLASSIC 9/27/2000 21 + 3 CLASSIC - VERSION 2 8/1/2014 21 + 3 CLASSIC - VERSION 3 8/5/2014 21 + 3 CLASSIC - VERSION 4 1/15/2019 21 + 3 PROGRESSIVE 1/24/2018 21 + 3 PROGRESSIVE - VERSION 2 11/13/2020 21 + 3 XTREME 1/19/1999 (V OF BLACKJACK) 21 + 3 XTREME - (PAYTABLE C) 2/23/2001 21 + 3 XTREME - (PAYTABLES D, E) 4/14/2004 21 + 3 XTREME - VERSION 3 1/13/2012 21 + 3 XTREME - VERSION 4 2/9/2012 21 + 3 XTREME - VERSION 5 3/6/2012 21 MADNESS 9/19/1996 21 MADNESS SIDE BET 4/1/1998 (V OF 21 MADNESS) 21 MAGIC 9/12/2011 (V OF BLACKJACK) 21 PAYS MORE 7/3/2012 (V OF BLACKJACK) 21 STUD 8/21/1997 NEW GAME 21 SUPERBUCKS 9/20/1994 (V OF 21) 211 POKER 7/3/2008 (V OF POKER) 24-7 BLACKJACK 4/15/2004 2G'$ 12/11/2019 2ND CHANCE BLACKJACK 6/19/2008 NEW GAME 2ND CHANCE BLACKJACK – VERSION 2 9/24/2008 2ND CHANCE BLACKJACK – VERSION 3 4/8/2010 3 CARD 6/24/2021 NEW GAME NAME OF GAME DATE OF APPROVAL COMMENTS 3 CARD BLITZ 8/22/2019 NEW GAME 3 CARD HOLD’EM 11/21/2008 NEW GAME 3 CARD HOLD’EM - VERSION 2 1/9/2009 -

Solitaire: Man Versus Machine
Solitaire: Man Versus Machine Xiang Yan∗ Persi Diaconis∗ Paat Rusmevichientong† Benjamin Van Roy∗ ∗Stanford University {xyan,persi.diaconis,bvr}@stanford.edu †Cornell University [email protected] Abstract In this paper, we use the rollout method for policy improvement to an- alyze a version of Klondike solitaire. This version, sometimes called thoughtful solitaire, has all cards revealed to the player, but then follows the usual Klondike rules. A strategy that we establish, using iterated roll- outs, wins about twice as many games on average as an expert human player does. 1 Introduction Though proposed more than fifty years ago [1, 7], the effectiveness of the policy improve- ment algorithm remains a mystery. For discounted or average reward Markov decision problems with n states and two possible actions per state, the tightest known worst-case upper bound in terms of n on the number of iterations taken to find an optimal policy is O(2n/n) [9]. This is also the tightest known upper bound for deterministic Markov de- cision problems. It is surprising, however, that there are no known examples of Markov decision problems with two possible actions per state for which more than n + 2 iterations are required. A more intriguing fact is that even for problems with a large number of states – say, in the millions – an optimal policy is often delivered after only half a dozen or so iterations. In problems where n is enormous – say, a googol – this may appear to be a moot point because each iteration requires Ω(n) compute time. In particular, a policy is represented by a table with one action per state and each iteration improves the policy by updating each entry of this table. -

Alaska Ecology Cards
F,W Traits: Mammal with forelegs modified to form membranous wings; keen eyesight; active at night Habitat: Forested areas with a lake nearby; roost in caves, tree cavities, or buildings. Foods: Mosquitoes, moths, mayflies, caddisflies; usually feeds over water and in forest openings Eaten by: Owls, squirrels Do You Know? Bats capture flying insects by using echolocation. A single bat may eat as many as I ,000 mosquitoes in one evening. A collection of 270 illustrations of one.-celled life, plants, invertebrates, fish, birds, and mammals found in Alaska Each illustration is backed by text describing the organism's traits, habitat, food habits, what other organisms eat it for food, and a "do you know?" fact. These cards are suitable for learners of any age. Primary educators may choose to adapt the illustrations and text for young readers. Alaska Ecology Cards REVISION 2001 Project Managers: Robin Dublin, Jonne Slemons Editors: Alaska Department of Fish and Game: Robin Dublin, Karen Lew Expression: Elaine Rhode Original Text: Susan Quinlan, Marilyn Sigman, Matt Graves Reviewers Past and Present: Alaska Department of Fish and Game: John Wright, The Alaska Department of Fish and Game Colleen Matt, Larry Aumiller, Jeff Hughes, jim Lieb, Gary has additional information and materials Miller, Mark Schwan, Rick Sinnott, Bill Taylor, Phyllis on wildlife conservation education. Weber~Scannell, Howard Golden, Mark Keech, Andy The Alaska Wildlife Curriculum includes: Alaska's EcologiJ & Wildlife Hoffmann, Fritz Kraus Alaska's Forests and Wildlife Alaska DEpartment of Natural Resources: Dan Ketchum Alaska's Tundra and Wildlife Cooperative Extention Service: Lois Bettini, Wayne Vandry Alaska's Wildlife for the Future U.S.D.A.