Mathematical Models of Seaside Operations in Container Ports and Their Solution
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

CH Brochure-Folder Pages V3 Final All Pages
| centrally located in Ipswich | high quality open-plan office suites to let www.crownhouse-ipswich.co.uk | location | Crown House has undergone an extensive refurbishment programme and now provides some of the highest quality office accommodation in the area. Ipswich is the county town and principal commercial The A12 and A14 trunk routes provide excellent road communications with the national motorway network, with Occupying a prominent position on Crown Street, part of Ipswich’s inner ring road, the central focus for this Major business occupiers in and around the town centre of Suffolk with a population of approximately Cambridge, Bury St Edmunds, Colchester, Chelmsford and Norwich within easy reach. The M25 and Stansted property is its superb setting. Crown House benefits from a multi-storey car park (1,160 spaces) to the rear, a include Legal & General, AXA, Associated British Ports, 130,000 people. Airport are within a one hour drive and the Ipswich railway station provides an inter-city service with a train cosmopolitan town centre immediately to the south, and the historic and beautiful Christchurch Park close by. Willis and Call Connect. Ipswich also benefits from a journey time to London (Liverpool Street) of approximately 70 minutes. The offices are on the cusp of a vibrant, expanding business and leisure area with shops including Marks & strong academic presence, being home to both New The Port of Felixstowe is within approximately 12 miles. Spencer, Debenhams and H&M. The town is home to a number of good quality hotels, restaurants and café bars, Suffolk College and University Campus Suffolk. -

Port of Felixstowe Logistics Park Build-To-Suit Distribution Warehouses up to 800,000 Sq.Ft Uniquely Placed to Serve the Nation 1.4 Million Sq.Ft | 68 Acres
PORT OF FELIXSTOWE LOGISTICS PARK BUILD-TO-SUIT DISTRIBUTION WAREHOUSES UP TO 800,000 SQ.FT UNIQUELY PLACED TO SERVE THE NATION 1.4 MILLION SQ.FT | 68 ACRES SINGLE BUILDING PORT OF FELIXSTOWE > HOME UP TO THE PORT OF BRITAIN 800,000 SQ.FT > PORT CENTRIC LOGISTICS The Port of Felixstowe is Britain’s busiest > AERIAL 1 container port and, as far as nationwide distribution is concerned, the most important. > AERIAL 2 The scale of its multi-modal operations dwarfs its competitors. Over 40% of the nation’s > MASTERPLAN containerised trade passes through the port 68 ACRES OF B8 LAND which, thanks to its optimal location, provides > WORKFORCE unrivalled connections to domestic and global markets. > ABOUT > CONTACTS BUILD-TO-SUIT DISTRIBUTION WAREHOUSES PORT OF FELIXSTOWE LOGISTICS PARK BUILD-TO-SUIT DISTRIBUTION WAREHOUSES UP TO 800,000 SQ.FT UNIQUELY PLACED TO SERVE THE NATION 1.4 MILLION SQ.FT | 68 ACRES THE BENEFITS OF > HOME W10* High Gauge Network PORT-CENTRIC forming part of the Strategic Rail > PORT CENTRIC LOGISTICS LOGISTICS Network (up to CP 5) > ROAD & SEA Increased transport costs, rising road GLASGOW Proposed future W10 loading gauge* > AERIAL 1 congestion and the challenges of transporting the largest containers inland are all making > AERIAL 2 port centric logistics more important to Freight Terminals cargo owners and their logistics providers. > MASTERPLAN * W10: Allows 2.9 m (9 ft 6 in) high Felixstowe’s location, multi-modality and Hi-Cube shipping containers to be sheer capacity explain why it is the preferred carried on standard -

4ALLPORTS News Update April 2021
4ALLPORTS News Update April 2021 ESB unveils renewables plans for ‘GREEN ATLANTIC @ Moneypoint’ News in brief: phases by ESB and opment of Money- 5G at Port of South Hampton: joint venture part- point will support the Verizon Business and Associated ners, Equinor. Once wider plans of Shan- British Ports have announced that complete, the wind non Foynes Port, and they will be working together to deploy private 5G at the Port of farm is expected to working with local Southampton. Delivered in part- be capable of power- stakeholders, help nership with Nokia, Verizon’s ing more than 1.6m make the Shannon private 5G platform will provide homes in Ireland. Estuary a focal point one of the United Kingdom’s (UK’s) busiest ports with a secure, Subject to the appro- for the offshore wind Image source: ESB low-latency private network con- priate consents being industry in Europe. nection. The Verizon private 5G ESB has announced this Synchronous Com- granted, the wind farm platform will provide ABP with a plans for a 'Green Atlan- pensator will be the is expected to be in ESB’s plans include private wireless data network across selected areas within the tic @ Moneypoint' site largest of its kind in production within the investment in a green East and West Docks of the Port. in County Clare, to be the world. This new next decade. hydrogen production, This will enable data communica- transformed into a plant will provide a storage and generation tions to be consolidated onto a green energy hub. range of electrical ser- ESB envisions that facility at Moneypoint single network. -

Hutchison Ports Our Business Divisions Ports and Related Services
THE WORLD’S LEADING PORT NETWORK EUROPE PRESENTATION JULY 2019 HUTCHISON PORTS OUR BUSINESS DIVISIONS PORTS AND RELATED SERVICES Hutchison Ports . The World’s Leading Port Network . 52 ports, 27 countries . 84.7 million TEU throughput in 2017 . A member of CK Hutchison Holdings, a renowned multinational conglomerate, with roots in Hong Kong 3 4 WE LEAD THROUGH THE CODE OF COMMON PRINCIPLES WE SHARE ACROSS OUR GLOBAL NETWORK 5 HUTCHISON PORTS EUROPE OUR BUSINESS DIVISIONS PORTS AND RELATED SERVICES Europe . The Netherlands (Rotterdam ECT, Amsterdam, Venlo, Moerdijk) . Belgium (Willebroek) . Germany (Duisburg) . Spain (Barcelona) . Sweden (Stockholm) . Poland (Gdynia) . UK (Felixstowe, Thamesport, Harwich) 7 HUTCHISON PORTS EUROPE Rotterdam . ECT Delta and Euromax terminals . 1st automated terminal in the world . Many shipping lines use ECT Delta as first port of call in Europe . Europe’s leading feeder hub . Handling ultra large container carriers with high productivity 8 HUTCHISON PORTS EUROPE Inland Terminals . Located in the Netherlands (Venlo, Moerdijk), Belgium (Willebroek) and Germany (Duisburg) . Extended gates between deepsea terminals in ECT to its European Gateway Services network . Sustainable and reliable tri-modal transport connections to hinterland 9 HUTCHISON PORTS EUROPE Amsterdam . Short sea hub with deep water -15m draft . Offering reliable tri-modal connections to hinterland with 3 rail tracks on terminal . Flexible well-trained non-unionised workforce, high productivity . Regular barge services to Rotterdam and Antwerp with 15 weekly departures . Sufficient capacity, fast truck turnaround and congestion free . Warehousing and added value services 10 HUTCHISON PORTS EUROPE Barcelona . 1st semi-auto terminal in Hutchison Ports . One of the most technologically advanced ports of all the Mediterranean . -
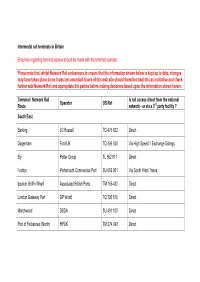
Intermodal Rail Terminals in Current Operation in Britain
Intermodal rail terminals in Britain Enquiries regarding terminal access should be made with the terminal operator. Please note that, whilst Network Rail endeavours to ensure that the information shown below is kept up to date, changes may have taken place since it was last amended. Users of this web site should therefore treat this as indicative and check further with Network Rail and appropriate 3rd parties before making decisions based upon the information shown herein. Terminal / Network Rail Is rail access direct from the national Operator OS Ref Route network - or via a 3rd party facility ? South East Barking JG Russell TQ 475 832 Direct Dagenham Ford UK TQ 498 828 Via High Speed 1 Exchange Sidings Ely Potter Group TL 562 811 Direct Fratton Portsmouth Commercial Port SU 655 001 Via South West Trains Ipswich Griffin Wharf Associated British Ports TM 166 432 Direct London Gateway Port DP World TQ 726 816 Direct Marchwood DSDA SU 401 105 Direct Port of Felixstowe (North) HPUK TM 274 343 Direct Port of Felixstowe (South) HPUK TM 286 326 Direct Southampton Western Docks Pentalver SU 397 121 Via Associated British Ports Purfleet CdMR TQ 566 774 Direct Southampton Maritime Freightliner SU 383 127 Direct Southampton Millbrook Freightliner SU 395 127 Direct Thamesport HPUK TQ 870 744 Via DB Schenker Tilbury Port (1) Freightliner TQ 628 768 Direct Tilbury Port (2) Tilbury Container Services TQ 624 760 Via Freightliner Tilbury Riverside Maritime Transport TQ 644 753 Direct LNE Cleveland (Wilton) Freightliner NZ 559 211 Direct Doncaster Freightliner -

United Kingdom, Port Facility Number
UNITED KINGDOM Approved port facilities in United Kingdom IMPORTANT: The information provided in the GISIS Maritime Security module is continuously updated and you should refer to the latest information provided by IMO Member States which can be found on: https://gisis.imo.org/Public/ISPS/PortFacilities.aspx Port Name 1 Port Name 2 Facility Name Facility Number Description Longitude Latitude AberdeenAggersund AberdeenAggersund AberdeenAggersund Harbour - Aggersund Board Kalkvaerk GBABD-0001DKASH-0001 PAXBulk carrier[Passenger] / COG 0000000E0091760E 000000N565990N [Chemical, Oil and Gas] - Tier 3 Aberdeen Aberdeen Aberdeen Harbour Board - Point GBABD-0144 COG3 0020000W 570000N Law Peninsular Aberdeen Aberdeen Aberdeen Harbour Board - Torry GBABD-0005 COG (Chemical, Oil and Gas) - 0000000E 000000N Marine Base Tier 3 Aberdeen Aberdeen Caledonian Oil GBABD-0137 COG2 0021000W 571500N Aberdeen Aberdeen Dales Marine Services GBABD-0009 OBC [Other Bulk Cargo] 0000000E 000000N Aberdeen Aberdeen Pocra Quay (Peterson SBS) GBABD-0017 COG [Chemical, Oil and Gas] - 0000000E 000000N Tier 3 Aberdeen Aberdeen Seabase (Peterson SBS) GBABD-0018 COG [Chemical, Oil and Gas] - 0000000E 000000N Tier 3 Ardrishaig Ardrishaig Ardrishaig GBASG-0001 OBC 0000000W 000000N Armadale, Isle of Armadale GBAMD-0001 PAX 0342000W 530000N Skye Ayr Ayr Port of Ayr GBAYR-0001 PAX [Passenger] / OBC [Other 0000000E 000000N Bulk Cargo] Ballylumford Ballylumford Ballylumford Power Station GBBLR-0002 COG [Chemical, Oil and Gas] - 0000000E 000000N Tier 1 Barrow in Furness Barrow in -

Darktrace Case Study: Harwich Haven Authority, UK Public Infrastructure
CASE STUDY Harwich Haven Authority Business Background Overview Harwich Haven Authority constitutes a major part of critical infrastructure in the UK, handling the world’s largest container ships. Through their Pilotage, Industry Vessel Traffic Services and supporting marine services, the Authority main- tains, preserves and protects important trade routes to and from the UK. Maritime With more than 40% of the UK’s container traffic passing through it, the Haven is an important gateway for European and global trade. The Authority Challenge delivers essential shipping services across five commercial ports including Port of Felixstowe, Ipswich, Navyard, Mistley and Harwich International. Mixed OT and IT environments Reliance on legacy systems Targeted and sophisticated cyber-attacks The power of Darktrace Industrial is amazing. It Results is critical that the trust port is fully operational Early detection of in-progress 24 hours a day, 365 days a year, and Darktrace cyber-threats Industrial helps us achieve this. 100% network visibility and investiga- Matt Calver, IT Infrastructure Engineer, tion capabilities Harwich Haven Authority Weekly Threat Intelligence Reports (TIRs) to highlight detected threats Challenge As critical national infrastructure, the ports under Harwich Haven Authority are attractive targets for cyber-criminals. A breach in Harwich Haven Authority’s networks could lead to the interruption of essential shipping services, physical harm to people, cargos and vessels, or the loss of commercial and personal data. In coordinating 15,000 ship movements per year, there is constant pressure on the Authority’s security team to ensure that these movements are secured against both indiscriminate and targeted cyber-threats. With both OT and IT networks to monitor and protect, Harwich Haven Authority’s strained security team was ill-equipped to identify threats at an early stage, and was particularly concerned by network activity indicating reconnaissance and vulnerability scans on its firewalls. -

UK Port Infrastructure Project Pipeline Analysis Report
Key 1. Port of Dover 2. Aberdeen Harbour 3. Tilbury Port 4. Port of Sheerness 5. Port of Felixstowe UK Port Infrastructure Project Pipeline 6. Port of Great Yarmouth 7. Dundee Port Analysis Report 8. Port of Montrose 18 9. Port of Tyne Prepared by Moffatt & Nichol, for the British 10. Blyth Ports Association, March 2018 11. Port of Bristol 12. Poole Harbour 2 Following release of the “Analysis of the National 13. Humber 8 Infrastructure and Construction Pipeline (6 December 2017)” 14. Port of Liverpool 7 by the Infrastructure and Projects Authority for the Cabinet 15. Port of Milford Haven Office and HM Treasury, an assessment has been 16. Shoreham Port undertaken by Moffatt & Nichol for the British Ports 17. Port of Holyhead Association (BPA). The objective is to summarise the 18. Port of Cromarty Firth forecasted development and construction pipeline for port infrastructure projects in the UK. 10 9 All information identified and described within this document has been based on publically available information from articles published within the last 12months. The research does not validate the viability of each proposed scheme and does not represent confirmation that the projects are in development. 17 14 13 Moffatt & Nichol is a global infrastructure advisory firm, specialising in projects where land meets water. With two offices in the UK, Moffatt & Nichol were well placed to 6 support BPA in providing a snapshot of the construction pipeline. 15 Moffatt & Nichol’s UK teams include specialists in Port and Terminal Planning, Coastal Engineering, Civil Engineering 11 5 and Maritime Market and Cargo Forecasting. -

Ipswich Economic Area Sector Needs Assessment Final Report
Ipswich Economic Area Sector Needs Assessment Final Report Ipswich Borough Council, Babergh District Council, Mid Suffolk District Council, Suffolk Coastal District Council September 2017 © 2017 Nathaniel Lichfield & Partners Ltd, trading as Lichfields. All Rights Reserved. Registered in England, no. 2778116. 14 Regent’s Wharf, All Saints Street, London N1 9RL Formatted for double sided printing. Plans based upon Ordnance Survey mapping with the permission of Her Majesty’s Stationery Office. © Crown Copyright reserved. Licence number AL50684A OurRef 13615682v8 Ipswich Economic Area Sector Needs Assessment : Final Report Executive Summary Lichfields has prepared this Sector Needs Assessment (SNA) on behalf of Ipswich, Babergh, Mid Suffolk and Suffolk Coastal councils. The purpose of the SNA is to provide a ‘business as usual’ assessment of the current and future growth potential of key sectors of the economy to help inform planning policy approaches to accommodating future economic growth and business needs across the Ipswich Economic Area (IEA). Forecasts of employment growth for each sector have been sourced from the 2016 East of England Forecasting Model (EEFM) for the period 2014-2036. These forecasts represent a ‘business as usual’ trajectory of growth based on recent economic trends within the study area and provide a starting point view of how the IEA’s economy may change over the coming years. Job growth that is higher than indicated by the EEFM could be brought about by policy or development interventions, and this is explored through consultation with a range of stakeholders including commercial agents, industry representatives and business organisations. Existing information and data sources relevant to each sector are also integrated within the analysis. -

Felixstowe Port Logistics Study Final Report for Suffolk Coastal District
In association with Felixstowe Port Logistics Study Final Report For Suffolk Coastal District Council October 2008 Felixstowe Port Logistics Study Suffolk Coastal District Council A report submitted by GHK in association with Haskoning UK Ltd. Date: 30/10/2008 526 Fulham Road, London SW6 5NR Tel: 020 7471 8000; Fax: 020 7736 0784 www.ghkint.com Document Control Document Felixstowe Port Logistics Study Prepared by Jamie Simpson (GHK), Colin Arnott (GHK), John Vercoe (RH) Checked by Andrew Davidge (GHK) Date 30 October 2008 Felixstowe Port Logistics Study Final Report October 2008 CONTENTS EXECUTIVE SUMMARY ....................................................................................................................I 1 INTRODUCTION..........................................................................................................................1 1.1 Objectives..................................................................................................................................1 1.2 Background ...............................................................................................................................1 1.3 Scope and Method ....................................................................................................................2 1.3.1 Data sources ..........................................................................................................................4 1.4 Report Structure ........................................................................................................................4 -

Port Privatisation: Ownership Involvement by External Companies
MASTER OF SCIENCE IN MARITIME SCIENCE MASTER DISSERTATION Academic year 2017 – 2018 Port privatisation: Ownership involvement by external companies Alan Johnson Submitted in partial fulfillment of the requirements Supervisor: Prof. dr. Theo Notteboom for the degree of: Master of Science in Maritime Science Assessor: Prof. Daan Schalck PERMISSION I declare that the content of this Master dissertation may be consulted or reproduced, provided that the source is referenced. Alan Johnson PREFACE This Master dissertation marks the conclusion of my advanced studies in the Master of Science in Maritime Science. I would like to explicitly thank certain people who have contributed to the realisation of this thesis. In the first place, I wish to express my sincere gratitude to my supervisor Prof. dr. Theo Notteboom and co-promotor Prof. Daan Schalck for their confidence and valuable feedback. Their willingness and assistance have resulted in the accomplishment of this dissertation. Furthermore, my appreciation goes to the interviewees for their cooperation and insights as well as to the respondents for completing the survey regarding my qualitative research. Many thanks go to my friends who are always available for advice. Their relentless and unconditional enthusiasm mean a lot to me. Last but not least, I am deeply grateful to my parents for the opportunity they have offered me to follow and finalise this additional master programme. Their exceptional support and motivation are extremely valuable for me. Alan Johnson Ghent, 24 January 2018 I II -

The Role of Sea Ports in End-To-End Maritime Transport Chain Emissions
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by MURAL - Maynooth University Research Archive Library Energy Policy 64 (2014) 337–348 Contents lists available at ScienceDirect Energy Policy journal homepage: www.elsevier.com/locate/enpol Energy and the Environment The role of sea ports in end-to-end maritime transport chain emissions David Gibbs a, Patrick Rigot-Muller b, John Mangan b,n, Chandra Lalwani c a Department of Geography, Environment and Earth Sciences, University of Hull, Kingston-upon-Hull HU6 7RX, United Kingdom b School of Marine Science and Technology, Newcastle University, Newcastle-upon-Tyne NE1 7RU, United Kingdom c Logistics Institute, Business School, University of Hull, Kingston-upon-Hull HU6 7RX, United Kingdom HIGHLIGHTS Investigates role of ports in mitigating GHG emissions in the end-to-end maritime transport chain. Emissions generated both by ports and by ships calling at ports are analysed. Shipping's emissions are far greater than those generated by port activities. Ports may have more impact through focusing efforts on reducing shipping's emissions. Options for ports to support and drive change in the maritime sector also considered. article info abstract Article history: This paper's purpose is to investigate the role of sea ports in helping to mitigate the GHG emissions Received 30 January 2013 associated with the end-to-end maritime transport chain. The analysis is primarily focused on the UK, Received in revised form but is international in application. The paper is based on both the analysis of secondary data and 29 August 2013 information on actions taken by ports to reduce their emissions, with the latter data collected for the Accepted 5 September 2013 main UK ports via their published reports and/or via interviews.