DOCSLIB.ORG

By Dr. Rawichote Chalodhorn (Choppy) Humanoid Robotics Lab, Neural System Group, Dept

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
By Dr. Rawichote Chalodhorn (Choppy) Humanoid Robotics Lab, Neural System Group, Dept Introduction to Humanoid Robotics by Dr. Rawichote Chalodhorn (Choppy) Humanoid Robotics Lab, Neural System Group, Dept. of Computer Science & Engineering, University of Washington. RoboCup soccer The brain controlled humanoid robot Outline • History of humanoid robots • Humanoid robots today • Androids • Analytical approaches of bipedal locomotion • Learning to walk through imitation • Future of humanoid robotics Atomaton: Leonardo's robot 1495 Atomaton: The Japanese tea serving doll 18th century to 19th century Honda E series Honda P series P1 P2 P3 1993 1996 1997 AIST / Kawada Industries : HRP series HRP-4C Androids • A robot that closely resembles a human • Human robot interaction Prof. Hiroshi Ishiguro ! Chapter 2 Zero-Moment Point (ZMP) The Zero-Moment Point [Vukobratovic et al. 1972] "#$!%&$'()*+!,#-%.$&!%&$+$/.$0!-!1&)-0!1-,23&)*/0!-/0!4(.$&-.*&$!+*&'$5!)6!.#$!1(%$0! 4),)7).(We)/!(/!&)1 ).can(,+8!9):$' $maintain&;!(.!)/45!1&($645!7$/WhatWhat.()/$ 0!balance.#$!<$&)=> ) 7isis$/.!? )(/ZMPZMP .!as (Zero(Zero MomentMoment Point)?Point)? @<>?A!-4)/3!:(.#!-!6$:!$B-7%4$+!)6!+.*0($+!.#-.!&$')4'$0!)/!(.+!,)/,$%.8!C:(/3!.)! .#$! 6-,.;long! .#-.! .#$! %&( /,(as%-4! 3) -4!the)6! .#$! %&)D$,.! ZMP:-+! .)! +.*05! is-/0! staying0$'$4)%! 1(%$0! #*7-/)(0!4),)7).()/!,)/.&)4!1-+$0!)/!.#$!<>?;!(.!:-+!0$,(0$0!.)!,)/,$/.&-.$!-!6*44! ,#-%.$&!.)!0(+,*++!(/!0$%.#!-44!.#$!-+%$,.+!)6!.#$!<>?;!6&)7!(.+!0$6(/(.()/!-/0!,)/,$%.;! .)!(.+!-%%within4(,-1(4(.5!@(/,4*0(/ 3the!%&$'()*+!+.*0($+A! support-/0!'-&(-/.+;!-/0! 6(/-445!polygon.(.+!0$&('-.()/8! 2.1 Definition ! ZMP Vukobratovic and Stepanenco, 1972 Center of Pressure" d R •ZMP NEVER! leaves the support polygon! E(3*&$!!F8GH!<$&)=>)7$/.!?)(/.!)&(3(/-4!0$6(/(.()/!@I*2)1&-•ZMP.)'(,!"#!$%&;!GJ JKcanA8! be measured by force sensors in feet. Zero-moment point Hiro Hirukawa The Onassis Foundation Lecture Series 2006 10/88 ! GL !"#$%&'()*(%"&(+&',-.,.&/%($,0/%( !"#$%&'(&#)*&+,--./&0123'&$2(&(2&4%$25'&(1'&4$'5(4#&#$6&#33"7'6&(1'&02$3(#$(&1'4%1(& #829'&43&:'52&+1&;&-/&(2&<4')6&#$&#00"5#('&9'5342$&2=&>?3*&&+,*@/&#$6&&+,*.-/A& 2 8 6 4 & 7 ' 6 & 7 4 ' 0 ) %3 3 # 3 !!!3 4 " !!!3 6 " 3 $ 35 35 !"#$$% 6+.$ ( 2 & 8 4 & 7 %3 3 !!!3 4 " 2 8 5 4 & 7 ' 5 & 7 4 ' 0 ) %3 3 # 3 !!!3 4 " !!!3 5 " 3 $ 36 36 !"#$"% 5+.$ ( 2 & 8 4 & 7 %3 3 !!!3 4 " >?"#(42$3&&+,*../&#$6&&+,*.,/&B'5'&"3'6&#)32&8<&C1#$%&+,--D/*& ! % A&E234(42$&9'0(25&2=&'- ' ( *6; 5 ; -+ % : !")$ . ( *% % % + A&(2(#)&(25?"'&#0(4$%&#(&'- , 6 5 4 !"($ 9 : : : : % !" , ( *. + &A&'F('5$#)&727'$(&:( + & 6 5 4 !"#$%&'()*(%"&(+&'9 ,-.,.&/%(3 $,0/%( * 9 9 9 9 % &A&'F('5$#)&=250'&9( + ( *<6 <5 <4 + &3 ' ' 9 9 9 9 % A&E234(42$&B1'5'&+9&43&#0(4$%& * ( *=6 = 5 =4 + !"#$%&'(&#)*&+,--./&0123'&' $2(&(2&4%$25'&(1'&4$'5(4#&#$6&#33"7'6&(1'&02$3(#$(&1'4%1(& # " #829'&43&:'52&+1&;&-/&(2&<4')6&#$&#00"5#('&9'5342$&2=&>?3*&&+,*@/&#$6&&+,*.-/A& & !"#$%&'()*(%"&(+&',-.,.&/%($,0/%( G4%"5'&&,*HA&I'=4$4(42$3&2=&9'0(253&=25&#&B#)J4$%&7'01#$437&+#6#E('6&=527&K#J#$4314&>?(@A*L&.@H@/*& 2 8 6 4 & 7 ' 6 & 7 4 ' 0 ) !"#$%&'(&#)*&+,--./&0123'&$2(&(2&%4%$25'&3 3 #(1'&3 !4$'5(4#&!!3 #$6&4 " #33"7!!!3 '6&(1'&6 "02$3(#$(&3 $ 351'4%1(&35 !"#$$% 6+.$ ( 2 & K#J#$4314&#829'&43&:'52&+>?(@A*&+.@H@/&1&;&-/&E5'3'$('6&(2&<4')6&#$&#00"5#('&#&6'549#(42$&9'5342$&2=&>?3*&&=25&8(1'&+,*@/&#$6&&4CMN&& 7 +,*.-/A&'?"#(42$3&B1401&4$0)"6'6& %3 3 !!!3 4 " 'F('5$#)& =250'3& #$6& 727'$(3& #002564$%& (2& (1'& 9'0(253O& 6'=4$4(42$3& #3& 312B$& 4$& 2 82 6 4 & 7 ' 6 & 7 4 ' 0 ) %3 3 # 3 !!!3 4 " !!!3 6 " 3 $ 35 35 6 ( 83 #53 !!4!3 & 7 4 "' !!5!3 & 7 5 "43 $' 0 36)36 +/01&2- -"#3*&!"#$$%P$4(4#))<L&(1'&=2))2B4$%&+.$Derivation%3 '?"#(42$&2 2=& of72(42$& the#(& ZMP#$&&#584(5#5<&E24$(&2$&(1'& !"#$"% 5+.$ ( 8 4 & 7 & %3 3 !!!3 2 4 " 8 4 & 7 %3 3 !!!3 4 " %52"$6&'-43&6'=4$'6L&B1401&43&#0?"45'6&2 8<&#EE)<4$%&6OQ)'78'5(&E54$04E)'A& 8 5 4 & 7 ' 5 & 7 4 ' 0 ) [Takanishi et al., 1989] %3 3 # 3 !!!3 4 " !!!3 5 " 3 $ 36 36 !"#$"% 5+.$ ( 2 & 8 !4 & 7 " 2 %3 3 !!3 4 >?"#(42$3&&+,*../&#$6&&+,*.,/&B'5'&"3'6&#)32&8<&C1#$%&+,--D/*&: 9 9 !"#$4% %#83 !&3 ' 6", !!&!3 & 0"$& . ' %, ' %#!* ' 6", + $( 5 & >?"#(42$3&&+,*../&3 #$6&&+,*.,/&B'5'&"3'6&#)32&8<&C1#$%&+,--D/*&: 9 ! % A&E234(42$&9'0(25&2=&'- ! ' ( *6; 5 ; -+ % A&E234(42$&9'0(25&2=&'- Q3&7'$(42$'6&'#5)4'5L&(1'&CMN&43&(1'&E24$(&4$&B1401&(1'&1254:2$(#)&027' ( *6; 5 ; -+ E2$'$(3&2=&(1'& % : !")$ . ( %% % % A&(2(#)&(25?"'&#0(4$%&#(&'- : !")$ . ( *% % %* +6 A&(2(#5)&(25?"4 '+&#0(4$%&#(&'- 727'$(&#5'&'?"#)& (2&,:'52*& R4(1& (143& 02$3(5#4$(L&6 (1'&5 #"(1253&4 7264=<&>?*&&+,*.D/&#$6& , ! ! 9 "($ "($ % 9 : : : : :: &A&'F(:'5$#)&72: 7%'$(&:( + !" , ( *. 6 . 5 . 4 + &A&'F('5$#)&727'$(&:( + !" , ( *. 6 . 5 . 4 + 5'(54'9'&+"34$%&347E)'&97#(1'&73 #(40#)&2E'5#(42$3/&(1'&S&#$6&T&027E2$'$(3&2=&(1'&CMNA& & % 9* 3 + 9 ( *< 9 < 9 < 9 + &A&'F('5$#)&=250'&9( * 6 9 5 4 9 9 9 % &A&'F('5$#)&=250'&9( & ' ' + ( *<6 <5 <4 + 3 % 9 * 9 ( *= 9 = 9 = 9 + A&E234(42$&B1'5'&+ &43&#0(4$%& &3 ' ' 6 5 4 ' 9 9 9 9 % A&E234(42$&B1'5'&+9&43&#0(4$%& # " * ( *=6 = 5 =4 + & # ' Vectors of a walking mechanism" G4%"5'&&,*HA&I'=4$4(42$3&2=&9'0(253&=25&#&B#)J4$%&7'01#$437&+#6#E('6&=527&K#J#$4314&>?(@A*L&.@H@/*& & & DU G4%"5'K#J#$4314&&&,*HA&I'=>?(4$4@A(4*&2+.@H@/&$3&2=&9E5'3'$('6&'0(253&=25#&&#6'549#(42$&&B#)J4$%&=25&7'0(1'&1#CMN&$437&'?"#(42$3&+#6#E('6&B1401&=527&K4$0)"6'6&#J#$4314&>?(@A*L&.@H@/*& 'F('5$#)& =250'3& #$6& 727'$(3& #002564$%& (2& (1'& 9'0(253O& 6'=4$4(42$3& #3& 312B$& 4$& +/01&2- -"#3*&P$4(4#))<L&(1'&=2))2B4$%&'?"#(42$&2=&72(42$&#(&#$&#584(5#5<&E24$(&2$&(1'& K#J#$4314&>?(@A*&+.@H@/&E5'3'$('6&#&6'549#(42$&=25&(1'&CMN&'?"#(42$3&B1401&4$0)"6'6& %52"$6&'-43&6'=4$'6L&B1401&43&#0?"45'6&8<&#EE)<4$%&6OQ)'78'5(&E54$04E)'A& 'F('5$#)& =250'3& #$6& 727'$(3& #002564$%& (2& (1'& 9'0(253O& 6'=4$4(42$3& #3& 312B$& 4$& 2 : 9 9 +/01&2- -"#3!"#$4%*&P$4(4#))<L& %#(1'&83 !&3 =2))2B4$%&' 6", !!&!3 & 0"$'?"#(42$&& . ' %, 2=&' %72(42$&#!* ' 6",#(&+ #$&$( 5#584(5#5<&& E24$(&2$&(1'& 3 : 9 %52"$6&'-43&6'=4$'6L&B1401&43&#0?"45'6&8<&#EE)<4$%&6OQ)'78'5(&E54$04E)'A& Q3&7'$(42$'6&'#5)4'5L&(1'&CMN&43&(1'&E24$(&4$&B1401&(1'&1254:2$(#)&027E2$'$(3&2=&(1'& 727'$(&#5'&'?"#)&2 (2&:'52*& R4(1&(143& 02$3(5#4$(L&(1'&#"(1253&7264=<&>?*&&+,*.D/&#$6& : 9 9 !"#$4%5'(54'9' &+"34$%%&347#E8)'3&!7&#3(1''76#"(,40#!)!&&!23 E&'50#(42$3/&"$& .(1'&'S&%#$6&,T&027' %E2$'$(3&#!* 2=&' (1'&6",CMNA&+ $( 5 & 3 : 9 Q3&7'$(42$'6&'#5)4'5L&(1'&CMN&43&(1'&E24$(&4$&B1401&(1'&1254:2$(#)&027E2$'$(3&2=&(1'& 727'$(& #5'&'?"#)& (2&:'52*& R4(1&(143& 02$3(5#4$(L&(1'&#"(1253&7264=<&>?*&&+,*.D/&#$6& & DU 5'(54'9'&+"34$%&347E)'&7#(1'7#(40#)&2E'5#(42$3/&(1'&S&#$6&T&027E2$'$(3&2=&(1'&CMNA& & DU Derivation of the ZMP !"#$%&'()*(%"&(+&',-.,.&/%($,0/%( ZMP equations with external forces and moments 3 : 7 2 ) 9 ( 7 ) 9 2 ) . 6 ) ( 1 * ' 1 '4 4 # 4 !!!4 2 " !!!4 7 " 4 $ ' 6 5 '1 % &5 !"#$%& 7+.$ + 3 ! : 2 ) 9 ( 8 1 '4 4 !!!4 2 " '1 2 !"#$%&'()*(%"&(+&',-.,.&/%($,0/%( [Takanishi et al., 1989] 3 : 7 2 ) 9 ( 7 ) 9 2 ) . 6 ) ( 1 * ' 1 '4 4 # 4 !!!4 2 " !!!4 5 " 4 $ ' 6 7 '1 % &7 !"#$)& 5+.$ + 3 ! !"#$%&'(&#)*&+,--./&0123'&$2(&(2&4%$25'&(1'&:4$'5(4#&2 ) 9#$6&(#33"78'16&(1'&02$3(#$(&1'4%1(& '4 4 !!!4 2 " '1 2 #829'&43&:'52&+1&;&-/&(2&<4')6&#$&#00"5#('&9'5342$&2=&>?3*&&+,*@/&#$6&&+,*.-/A& "#$%!&''()&*#!+&%!,%-.!$/!A%-0-(&1! simplified%2,.$-% version!34!2#-!&,2#)(%! of ZMP&/.! equations)2#-(!(-%-&(*#-(%!56$(;<( 2 8 6 4 & 7 ' 6 & 7 4 ' 0 ) =>?7!8998:!;&(<!=!>#--7!899?:!"&<&/$%#$%3 3 #(;<(=>?3 !!!3 7!899@AB!4 " !!!3 6 " 3 $ 35 35 !"#$$% 6+.$ ( 2 & 8 4 & 7 %3 3 !!!3 4 " [Huang et al., 2001] 2 8 5 4 & 7 ' 5 & 7 4 ' 0 ) %3 3 # 3 !!!3 4 " !!!3 5 " 3 $ 36 36 !"#$"% 5+.$ ( 2 & 8 4 & 7 %3 3 !!!3 4 " >?"#(42$3&&+,*../&#$6&&+,*.,/&B'5'&"3'6&#)32&8<&C1#$%&+,--D/*& ! % A&E234(42$&9'0(25&2=&'- ' ( *6; 5 ; -+ ! % A&(2(#)&(25?"'&#0(4$%&#(&'- : ")$ . ( *%6 %5 %4 + , ! 9 "($ % : : : : &A&'F('5$#)&727'$(&:( + !" , ( *. 6 . 5 . 4 + 9 &3 * 9 9 9 9 % &A&'F('5$#)&=250'&9( + ( *<6 <5 <4 + &3 ' ' 9 9 9 9 % A&E234(42$&B1'5'&+9&43&#0(4$%& * ( *=6 = 5 =4 + ' # " & G4%"5'&&,*HA&I'=4$4(42$3&2=&9'0(253&=25&#&B#)J4$%&7'01#$437&+#6#E('6&=527&K#J#$4314&>?(@A*L&.@H@/*& K#J#$4314&>?(@A*&+.@H@/&E5'3'$('6&#&6'549#(42$&=25&(1'&CMN&'?"#(42$3&B1401&4$0)"6'6& 'F('5$#)& =250'3& #$6& 727'$(3& #002564$%& (2& (1'& 9'0(253O& 6'=4$4(42$3& #3& 312B$& 4$& +/01&2- -"#3*&P$4(4#))<L&(1'&=2))2B4$%&'?"#(42$&2=&72(42$&#(&#$&#584(5#5<&E24$(&2$&(1'& %52"$6&'-43&6'=4$'6L&B1401&43&#0?"45'6&8<&#EE)<4$%&6OQ)'78'5(&E54$04E)'A& 2 : 9 9 !"#$4% %#83 !&3 ' 6", !!&!3 & 0"$& .
Load more

Recommended publications
  • Honda Insight Wikipedia in Its Third Generation, It Became a Four-Door Sedan €”Present
    Honda insight wikipedia In its third generation, it became a four-door sedan —present. It was Honda's first model with Integrated Motor Assist system and the most fuel efficient gasoline-powered car available in the U. The Insight was launched April in the UK as the lowest priced hybrid on the market and became the best selling hybrid for the month. The Insight ranked as the top-selling vehicle in Japan for the month of April , a first for a hybrid model. In the following month, December , Insight became the first hybrid available in North America, followed seven months later by the Toyota Prius. The Insight featured optimized aerodynamics and a lightweight aluminum structure to maximize fuel efficiency and minimize emissions. As of , the first generation Insight still ranks as the most fuel-efficient United States Environmental Protection Agency EPA certified gasoline-fueled vehicle, with a highway rating of 61 miles per US gallon 3. The first-generation Insight was manufactured as a two-seater, launching in a single trim level with a manual transmission and optional air conditioning. In the second year of production two trim levels were available: manual transmission with air conditioning , and continuously variable transmission CVT with air conditioning. The only major change during its life span was the introduction of a trunk-mounted, front-controlled, multiple-disc CD changer. In addition to its hybrid drive system, the Insight was small, light and streamlined — with a drag-coefficient of 0. At the time of production, it was the most aerodynamic production car to be built.
    [Show full text]
  • Gait-Behavior Optimization Considering Arm Swing and Toe Mechanisms for Biped Robot on Rough Road
    Gait-Behavior Optimization Considering Arm Swing and Toe Mechanisms for Biped Robot on Rough Road Author: Supervisor: NGUYEN VAN TINH Professor. Dr. Eng. Student ID: NB16508 HIROSHI HASEGAWA A DISSERTATION SUBMITTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY September, 2019 i Declaration of Authorship • This work was done wholly or mainly while in candidature for a research de- gree at this University. • Where any part of this thesis has previously been submitted for a degree or any other qualification at this University or any other institution, this has been clearly stated. • Where I have consulted the published work of others, this is always clearly attributed. • Where I have quoted from the work of others, the source is always given. With the exception of such quotations, this thesis is entirely my own work. • I have acknowledged all main sources of help. • Where the thesis is based on work done by myself jointly with others, I have made clear exactly what was done by others and what I have contributed my- self. Signed: Date: ii Abstract This research addresses a gait generation approach for the biped robot which is based on considering that a gait pattern generation is an optimization problem with constraints where to build up it, Response Surface Model (RSM) is used to approxi- mate objective and constraint function, afterwards, Improved Self-Adaptive Differ- ential Evolution Algorithm (ISADE) is applied to find out the optimal gait pattern for the robot. In addition, to enhance stability of walking behavior, I apply a foot structure with toe mechanism.
    [Show full text]
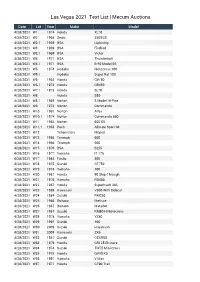
  • Las Vegas 2021 Text List | Mecum Auctions
    Las Vegas 2021 Text List | Mecum Auctions Date Lot Year Make Model 4/28/2021 W1 1974 Honda XL70 4/28/2021 W2 1968 Sears 250SGS 4/28/2021 W2.1 1969 BSA Lightning 4/28/2021 W3 1969 BSA Firebird 4/28/2021 W3.1 1969 BSA Victor 4/28/2021 W4 1971 BSA Thunderbolt 4/28/2021 W4.1 1971 BSA B-50 Model SS 4/28/2021 W5 1974 Hodaka Motocross 100 4/28/2021 W5.1 Hodaka Super Rat 100 4/28/2021 W6 1964 Honda CB750 4/28/2021 W6.1 1973 Honda CB450 4/28/2021 W7.1 1973 Honda SL70 4/28/2021 W8 Honda S90 4/28/2021 W8.1 1969 Norton S Model Hi-Pipe 4/28/2021 W9 1973 Norton Commando 4/28/2021 W10 1967 Norton Atlas 4/28/2021 W10.1 1974 Norton Commando 850 4/28/2021 W11 1962 Norton 650 SS 4/28/2021 W11.1 1963 Puch Allstate Sport 60 4/28/2021 W12 Teliamotors Moped 4/28/2021 W13 1956 Triumph 650 4/28/2021 W14 1966 Triumph 500 4/28/2021 W15 1970 BSA B255 4/28/2021 W16 1977 Yamaha IT 175 4/28/2021 W17 1984 Fantic 300 4/28/2021 W18 1975 Suzuki GT750 4/28/2021 W19 1974 Yamaha 100 4/28/2021 W20 1967 Honda 90 Step-Through 4/28/2021 W21 1976 Yamaha RD400 4/28/2021 W22 1967 Honda Superhawk 305 4/28/2021 W23 1999 Kawasaki V800 With Sidecar 4/28/2021 W24 1984 Suzuki RM250 4/28/2021 W25 1966 Bultaco Metisse 4/28/2021 W26 1967 Bultaco Matador 4/28/2021 W27 1987 Suzuki RM80 H Motocross 4/28/2021 W28 1978 Yamaha YZ80 4/28/2021 W29 1994 Suzuki 400 4/28/2021 W30 2009 Suzuki Hayabusa 4/28/2021 W31 2009 Kawasaki ZX6 4/28/2021 W32 1987 Suzuki GSXR50 4/28/2021 W33 1979 Honda CR125 Elsinore 4/28/2021 W34 1974 Suzuki TM75 Mini-Cross 4/28/2021 W35 1975 Honda QA50 K3 4/28/2021 W36 1997 Yamaha
    [Show full text]
  • Master Thesis Robot's Appearance
    VILNIUS ACADEMY OF ARTS FACULTY OF POSTGRADUATE STUDIES PRODUCT DESIGN DEPARTMENT II YEAR MASTER DEGREE Inna Popa MASTER THESIS ROBOT’S APPEARANCE Theoretical part of work supervisor: Mantas Lesauskas Practical part of work supervisor: Šarūnas Šlektavičius Vilnius, 2016 CONTENTS Preface .................................................................................................................................................... 3 Problematics and actuality ...................................................................................................................... 3 Motives of research and innovation of the work .................................................................................... 3 The hypothesis ........................................................................................................................................ 4 Goal of the research ................................................................................................................................ 4 Object of research ................................................................................................................................... 4 Aims of Research ..................................................................................................................................... 5 Sources of research (books, images, robots, companies) ....................................................................... 5 Robots design .........................................................................................................................................
    [Show full text]
  • Master's Thesis
    MASTER'S THESIS Developing a ROS Enabled Full Autonomous Quadrotor Ivan Monzon 2013 Master of Science in Engineering Technology Engineering Physics and Electrical Engineering Luleå University of Technology Department of Computer Science, Electrical and Space Engineering Developing a ROS Enabled Full Autonomous Quadrotor Iv´anMonz´on Lule˚aUniversity of Technology Department of Computer science, Electrical and Space engineering, Control Engineering Group 27th August 2013 ABSTRACT The aim of this Master Thesis focuses on: a) the design and development of a quadrotor and b) on the design and development of a full ROS enabled software environment for controlling the quadrotor. ROS (Robotic Operating System) is a novel operating system, which has been fully oriented to the specific needs of the robotic platforms. The work that has been done covers various software developing aspects, such as: operating system management in different robotic platforms, the study of the various forms of program- ming in the ROS environment, evaluating building alternatives, the development of the interface with ROS or the practical tests with the developed aerial platform. In more detail, initially in this thesis, a study of the ROS possibilities applied to flying robots, the development alternatives and the feasibility of integration has been done. These applications have included the aerial SLAM implementations (Simultaneous Location and Mapping) and aerial position control. After the evaluation of the alternatives and considering the related functionality, au- tonomy and price, it has been considered to base the development platform on the Ar- duCopter platform. Although there are some examples of unmanned aerial vehicles in ROS, there is no support for this system, thus proper design and development work was necessary to make the two platforms compatible as it will be presented.
    [Show full text]
  • Chapter 6. Evolution of Legged Machines and Robots
    excerpt from the book: Marko B. Popovic, Biomechanics and Robotics, Pan Stanford Publishing Pte. Ltd., 2013 (No of pages 351) Print ISBN: 9789814411370, eBook ISBN: 9789814411387, DOI: 10.4032/9789814411387 Copyright © 2014 by Pan Stanford Publishing Pte. Ltd. Chapter 6. Evolution of Legged Machines and Robots Chapter outline: Early Legged Machines in the 19th Century 193 Legged Machines in the First Half of the 20th Century 195 Legged Machines during 1950–1970 196 Legged Robots during 1970–1980 197 Legged Robots during 1980–1990 199 Legged Robots during 1990–2000 204 Legged Robots since 2000 208 References and Suggested Reading 214 [chapter content intentionally omitted] References: About AIBO, http://www.sonyaibo.net/aboutaibo.htm. Retrieved July 2012. Asimo by Honda, history, http://asimo.honda.com/asimo-history/. Retrieved July 2012. ASIMO—Wikipedia, the free encyclopedia, http://en.wikipedia.org/wiki/ASIMO. Retrieved July 2012. BBC News—Robotic cheetah breaks speed record for legged robots, (BBC News Technology 6 March 2012) http://www.bbc.com/news/technology-17269535. Retrieved July 2012. Big Muskie’s Bucket, McConnelsville, Ohio, http://www.roadsideamerica.com/story/2184. Retrieved July 2012. Boston Dynamics: Dedicated to the Science and Art of How Things Move; http://www.bostondynamics.com/robot_bigdog.html. Retrieved July 2012. Chavez-Clemente, D., “Gait Optimization for Multi-legged Walking Robots, with Application to a Lunar Hexapod”, PhD Dissertation, the Stanford University Department of Aeronautics and Astronautics, January 2011. Cox, W., “Big muskie”, The Ohio State Engineer, p. 25–52, 1970. Cyberneticzoo.com. Early Humanoid Robots, http://cyberneticzoo.com/?page_id=45. Retrieved July 2012. Cyberneticzoo.com.
    [Show full text]
  • Humanoid Robot: ASIMO
    Special Issue - 2017 International Journal of Engineering Research & Technology (IJERT) ISSN: 2278-0181 ICADEMS - 2017 Conference Proceedings Humanoid Robot: ASIMO 1Vipul Dalal 2Upasna Setia Department of Computer Science & Engineering, Department of Computer Science & Engineering, GITAM Kablana(Jhajjar), India GITAM Kablana (Jhajjar), India Abstract:Today we find most robots working for people in It has been suggested that very advanced robotics will industries, factories, warehouses, and laboratories. Robots are facilitate the enhancement of ordinary humans. useful in many ways. For instance, it boosts economy because businesses need to be efficient to keep up with the industry Although the initial aim of humanoid research was to build competition. Therefore, having robots helps business owners to better orthotics and prosthesis for human beings, knowledge be competitive, because robots can do jobs better and faster than has been transferred between both disciplines. A few humans can, e.g. robot can built, assemble a car. Yet robots examples are: powered leg prosthesis for neuromuscular cannot perform every job; today robots roles include assisting impaired, ankle-foot orthotics, biological realistic leg research and industry. Finally, as the technology improves, there prosthesis and forearm prosthesis. will be new ways to use robots which will bring new hopes and new potentials. Besides the research, humanoid robots are being developed to perform human tasks like personal assistance, where they Index Terms--Humanoid robots, ASIMO, Honda. should be able to assist the sick and elderly, and dirty or dangerous jobs. Regular jobs like being a receptionist or a I. INTRODUCTION worker of an automotive manufacturing line are also suitable A HUMANOID ROBOT is a robot with its body shape built for humanoids.
    [Show full text]
  • Honda Motor Company
    ŠKODA AUTO a.s., Střední odborné učiliště strojírenské, odštěpný závod Honda motor company Jakub Kareš ŠKODA AUTO a.s., Střední odborné učiliště strojírenské, odštěpný závod obor: 39-41-L/51 Autotronik třída: X2. školní rok: 2016/2017 Zadání maturitní práce pro: Jakub Kareš předmět: Odborné předměty zadání: Honda motor co. vedoucí maturitní práce: Ing. Jan Heidler termín odevzdání maturitní práce: 31.03.2017 Prohlášení Prohlašuji, že jsem maturitní práci na téma Komfortní výbava automobilů vypracoval samostatně s využitím uvedených pramenů a literatury. V Mladé Boleslavi dne 27.03.2017 Podpis:…………………………………………………………………… Obsah 1. Úvod ............................................................................................................................. 2 2. Historie ......................................................................................................................... 2 3. VTEC ............................................................................................................................. 3 4. Typy výrobků ................................................................................................................. 6 5. VIN ............................................................................................................................. 19 6. Závěr ........................................................................................................................... 20 7. Poděkování, zdroje .....................................................................................................
    [Show full text]
  • Now It Needs You
    Wikipedia is there when you need it — now it needs you. $1.4M USD $7.5M USD Donate Now [Hide] [Show] Wikipedia Forever Our shared knowledge. Our shared treasure. Help us protect it. [Show] Wikipedia Forever Our shared knowledge. Our shared treasure. Help us protect it. Honda From Wikipedia, the free encyclopedia Jump to: navigation, search This article is about the multinational corporation. For other uses, see Honda (disambiguation). This article contains Japanese text. Without proper rendering support, you may see question marks, boxes, or other symbols instead of kanji and kana. Honda Motor Company, Ltd. Honda Giken Kogyo Kabushiki-gaisha 本田技研工業株式会社 Public Type (TYO: 7267) & (NYSE: HMC) Founded 24 September 1948 Soichiro Honda Founder(s) Takeo Fujisawa Headquarters Minato, Tokyo, Japan Area served Worldwide Satoshi Aoki (Chairman) Key people Takanobu Ito (CEO) Automobile Industry Truck manufacturer Motorcycle automobiles, trucks, motorcycles, scooters, ATVs, electrical generators, robotics, Products marine equipment, jets, jet engines, and lawn and garden equipment. Honda and Acura brands. Revenue ▲ US$ 120.27 Billion (FY 2009)[1] Operating ▲ US$ 2.34 Billion (FY 2009)[1] income Net income ▲ US$ 1.39 Billion (FY 2009)[1] Total assets ▼ US$ 124.98 Billion (FY 2009)[1] Total equity ▼ US$ 40.6 Billion (FY 2009)[1] Employees 181876[2] Website Honda.com Honda Motor Company, Ltd. (Japanese: 本田技研工業株式会社, Honda Giken Kōgyō Kabushiki- gaisha ?, Honda Technology Research Institute Company, Limited) listen (help·info) (TYO: 7267) is a Japanese multinational corporation primarily known as a manufacturer of automobiles and motorcycles. Honda was the first Japanese automobile manufacturer to release a dedicated luxury brand, Acura in 1986.
    [Show full text]
  • Eg 1200X Generator Manual
    Eg 1200x Generator Manual Generac Parts Generac Generator Parts and Breakdowns. How to find what you need? Generac Technical Manual For R-100 Digital Controller: Models 05210-0, 05211-0, 05212-0, http://www.generator-parts.com/ Generac EG1000 Portable Petrol Generator, was Generac EG1000 Portable Petrol Generator Closed 28 May 2014 see similar item on sale now at CQout Online Auctions large range of Tools, Hardware & DIY items on sale http://www.cqout.com/item.asp?id=11885112 Shop for Your Honda Car - Official Honda Web Site Get price quotes and compare Honda hybrids, cars, trucks, SUVs and crossovers at the Official Honda Web site. See full specs and locate a dealer now. http://automobiles.honda.com/shop/ Kubota Engine America Trust the proven reliability & clean performance of Kubota Engines, Generators and Parts. V3800-CR-TE4. Kubota s industrial SPARK IGNITED ENGINE LINE UP http://www.kubotaengine.com/ DM TECH AG-HPX500P LOI ANLEITU - Manuals manualsbuzz.com - Privacy Policy - About & Contact form Manuals Network Inc 3004 INSTRUCCIONES HONDA GENERATOR EG 1200X ISTRU HOFMAN AEG LAVATHERM 8080 http://www.manualsbuzz.com/results.php?lang=de&search=DM%20TECH%20AG- HPX500P%20LOI%20ANLEITU GE Energy - Official Site Heavy Duty Gas Turbines, Steam Turbines & Generators; GE Energy Management designs technology solutions for the transmission, distribution, management, http://www.ge-energy.com/ Atlas Copco - Official Site Welcome to the Atlas Copco Group's corporate website http://www.atlascopco.com/us/system/splash.aspx American Honda Motor Company - Official Site Explore an innovative line of quality products from American Honda Motor Company. Find the latest news and information on Honda and Acura brand products.
    [Show full text]
  • AI Business Update 2017
    PT ASTRA INTERNATIONAL TBK Full Year 2017 - Results Presentation Disclaimer The materials in this presentation have been prepared by PT Astra International Tbk (Astra) and are general background information about Astra Group business performances current as at the date of this presentation and are subject to change without prior notice. This information is given in summary form and does not purport to be complete. Information in this presentation, including forecast financial information, should not be considered as advice or a recommendation to investors or potential investors in relation to holding, purchasing or selling securities or other financial products or instruments and does not take into account their particular investment objectives, financial situation or needs. Before acting on any information, readers should consider the appropriateness of the information having regard to these matters, any relevant offer document and in particular, readers should seek independent financial advice. This presentation may contain forward looking statements including statements regarding our intent, belief or current expectations with respect to Astra businesses and operations, market conditions, results of operation and financial condition, capital adequacy, specific provisions and risk management practices. Readers are cautioned not to place undue reliance on these forward looking statements; past performance is not a reliable indication of future performance. Astra does not undertake any obligation to publicly release the result of any revisions
    [Show full text]
  • Mcdc) 2013-2014
    Multinational Capability Development Campaign (MCDC) 2013-2014 Focus Area “Role of Autonomous Systems in Gaining Operational Access” _____________________________ Proceedings Report Autonomous Systems Focus Area 1 This document was developed and written by the contributing nations and international organisations of the Multinational Capability Development Campaign (MCDC) 2013-14. It does not necessarily reflect the official views or opinions of any single nation or organisation, but is intended as a recommendation for national/international organisational consideration. Reproduction of this document and unlimited distribution of copies is authorised for personal and non-commercial use only, provided that all copies retain the author attribution as specified below. The use of this work for commercial purposes is prohibited; its translation into other languages and adaptation/modification requires prior written permission. Questions concerning distribution and use can be referred to [email protected] PARTICIPANTS & ROLES: Focus Area Project Lead: NATO Allied Command Transformation Contributing Nations/Organizations: Austria, Czech Republic, Finland, Poland, Switzerland, United Kingdom and United States Observers: Germany, European Union, The Netherlands, Sweden The Netherlands formally joined this project as an observer but also made a substantial contribution. 2 Contents Preface .................................................................................................................................................... 4
    [Show full text]