Modelling Two Dimensional Affected Regions by “Seca” Disease with Proximity Diagrams †
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

25 Years of the Leader Initiative As European Rural Development Policy: the Case of Extremadura (Sw Spain)
Europ. Countrys. · 2· 2017 · p. 302-316 DOI: 10.1515/euco-2017-0019 European Countryside MENDELU 25 YEARS OF THE LEADER INITIATIVE AS EUROPEAN RURAL DEVELOPMENT POLICY: THE CASE OF EXTREMADURA (SW SPAIN) Ana Nieto Masot1; Gema Cárdenas Alonso2 1 Prof. Dr. Ana Nieto Masot, Department of Arts and Territory Science, University of Extremadura, Av. Universidad, University Campus Cáceres. [email protected] 2 Lic. Gema Cárdenas Alonso Department of Arts and Territory Science, University of Extremadura, Av. Universidad, University Campus Caceres. [email protected] 302/396 Received 2 September 2016; Accepted 3 March 2017 Abstract: For 25 years the rural development policy has been implemented through the LEADER Approach in the EU to reduce differences between rural and urban areas, as well as to satisfy the basic needs of the population. In this paper, Extremadura is analysed, which is a Spanish region where LEADER has been applied since its inception in 1991. The objective is to assess if the distribution of rural development aids has been influenced by the diverse demographic and socioeconomic realities that Extremadura presents from the analysis of variables that represent these realities on the territory through a GIS. Following this methodology, it has been noticed that the largest investments have been executed in the most developed rural areas of the region. Key words: Rural development, LEADER Approach, Local Action Group, Geographic Information System Resumen: Durante los últimos 25 años se viene implantando la Política de Desarrollo Rural europea bajo el conocido como Método LEADER, cuyo fin es reducir las diferencias existentes entre las zonas rurales y las urbanas de la UE, así como satisfacer las necesidades básicas de su población. -

Paleomagnetism in Extremadura (Central Iberian Zone, Spain) Paleozoic Rocks: Extensive Remagnetizations and Further Constraints
Paleomagnetism in Extremadura (Central Iberian zone, Spain) Paleozoic rocks: extensive remagnetizations and further constraints on the extent of the Cantabrian orocline Daniel Pastor-Galán, Gabriel Gutiérrez- Alonso, Mark J. Dekkers & Cor G. Langereis Journal of Iberian Geology Including Latin America and the Mediterranean ISSN 1698-6180 Volume 43 Number 4 J Iber Geol (2017) 43:583-600 DOI 10.1007/s41513-017-0039-x 1 23 Your article is protected by copyright and all rights are held exclusively by Springer International Publishing AG. This e-offprint is for personal use only and shall not be self- archived in electronic repositories. If you wish to self-archive your article, please use the accepted manuscript version for posting on your own website. You may further deposit the accepted manuscript version in any repository, provided it is only made publicly available 12 months after official publication or later and provided acknowledgement is given to the original source of publication and a link is inserted to the published article on Springer's website. The link must be accompanied by the following text: "The final publication is available at link.springer.com”. 1 23 Author's personal copy J Iber Geol (2017) 43:583–600 https://doi.org/10.1007/s41513-017-0039-x RESEARCH PAPER Paleomagnetism in Extremadura (Central Iberian zone, Spain) Paleozoic rocks: extensive remagnetizations and further constraints on the extent of the Cantabrian orocline 1 2,3 4 Daniel Pastor-Gala´n • Gabriel Gutie´rrez-Alonso • Mark J. Dekkers • Cor G. Langereis4 -

DATOS SOBRE EL LOBO IBÉRICO ( Canis Lupus Signatus CABRERA, 1907) EN EXTREMADURA
GalemysEl 12 lobo (nº en especial), Extremadura 2000 DATOS SOBRE EL LOBO IBÉRICO ( Canis lupus signatus CABRERA, 1907) EN EXTREMADURA M. RICO, L. LLANEZA, P. FERNÁNDEZ-LLARIO Y J. CARRANZA Cátedra de Biología y Etología. Fac. Veterinaria.Univ. Extremadura. 10071 Cáceres. ([email protected]) RESUMEN El presente estudio tiene como objetivo determinar el estatus poblacional del Lobo ibérico (Canis lupus signatus) en Extremadura. El ámbito de estudio se circunscribe al área de distribución, previa- mente descrita por varios autores. Se presentan los resultados correspondientes al trabajo de campo realizado en verano/otoño de 1997 y 1998 en la Sierra de San Pedro y en la Sierra de Gata. Se ha desarro- llado una metodología destinada a la localización de grupos reproductores y, de modo general, a la de- terminación de presencia/ausencia de la especie. Para ello se han realizado campañas de campo consis- tentes en itinerarios (recorridos a pie) en el área de estudio, cubriendo amplios sectores, en función de las zonas potencialmente más usadas por los lobos. Durante 1997, en la Sierra de San Pedro se realiza- ron 64 recorridos, que suponen 692 km, y en Gata, 32 recorridos, con 431 km. En 1998 se han realizado 23 recorridos (228 km) en San Pedro y 12 recorridos en Gata (116 Km). El trabajo de campo se ha llevado a cabo de manera conjunta, en los bordes fronterizos de España y Portugal, con investigadores de la Universidad de Lisboa. En las prospecciones efectuadas en las sierras de San Pedro y de Gata no se ha podido confirmar la presencia de grupos reproductores. -
Rural Tourism As a Development Strategy in Low-Density Areas: Case Study in Northern Extremadura (Spain)
sustainability Article Rural Tourism as a Development Strategy in Low-Density Areas: Case Study in Northern Extremadura (Spain) Ana Nieto Masot * and Nerea Ríos Rodríguez Department of Art and Territorial Sciences, University of Extremadura, 10003 Caceres, Spain; [email protected] * Correspondence: [email protected] Abstract: The appearance of new trends and models of tourism consumption has allowed the proliferation of rural tourist facilities in northern Extremadura. This article analyzes the economic, social, and heritage (natural and cultural) variables to relate them to the tourism offer and demand in these areas. The present study used geostatistical techniques such as Principal Component Analysis (PCA) and their spatial location through Geographic Information Systems (GIS) to determine the distribution and degree of incidence of these variables in the territories. The results obtained confirm the existence of imbalances in the tourism sector, which made it possible to determine which tourist territories have implemented the best lines of action to receive visitors, increase economic income, and preserve the population in rural areas with deficiencies in their tourism development. Keywords: rural tourism; travelers; principal component analysis; geographic information systems; tourist accommodation; Extremadura 1. Introduction Tourism has been an economic sector of great importance and has undergone devel- opment, especially since the middle of the 20th century, when it was consolidated as a Citation: Nieto Masot, A.; Ríos mass phenomenon. From the 1960s onwards, the tourism sector in Spain began to have Rodríguez, N. Rural Tourism as a an important role in the country’s economy, as well as being used to end the isolation that Development Strategy in the country had due to the Franco dictatorship. -

Environmental and Social Data Sheet
Luxembourg, 11 November 2020 Public Environmental and Social Data Sheet Overview Project Name: AVE MADRID EXTREMADURA Project Number: 2020-0033 Country: Spain Project Description: Construction of a new high speed railway line Talayuela – Plasencia – Cáceres – Mérida - Badajoz (around 260 km). The project is part of the high speed rail line Madrid - Extremadura and will improve cross-border connections with Portugal in the Atlantic TEN-T corridor. EIA required: Yes Project included in Carbon Footprint Exercise1: Yes (details for projects included are provided in section: “EIB Carbon Footprint Exercise”) Environmental and Social Assessment Environmental Assessment The project is included in the Infrastructure, Transport and Housing Master Plan “Plan de Infraestructuras, Transporte y Vivienda PITVI (2012-2024)”, which has been subject of a Strategic Environmental Assessment (SEA) in accordance with Directive 2001/42/EC. It was also included in the earlier strategic plans, such as the “Strategic Plan for Transport Infrastructure 2005-2020”, which was also subject of a SEA. Most of the project is on new alignment and falls within the scope of Annex I of the Environmental Impact Assessment (EIA) Directive (Directive 2011/92/EU as amended by 2014/52/EU). In particular, the following 4 separate EIA procedures were carried out for the different components of the project with the corresponding public consultation and publication of the environmental consents (Declaración de Impacto Ambiental, DIA) in the State Official Bulletin (Boletín Oficial -

Inicio Segunda Edicion Inglés.Cdr
COUNTRY WALKS of Extremadura 24 COUNTRY WALKS that invite you to admire the beautiful surroundings and landscapes rich in history and nature. © Extremadura Rural Development Network (REDEX). 2019. INDEX: Extremadura Rural Development Network (REDEX)................................................................................................ Page 2 - 3 Country Walks of Extremadura................................................................................................................................................... Page 4 - 5 Recommendations...................................................................................................................................................................................... Page 6 - 7 Relation of Country Walks............................................................................................................................................................. Page 8 - 55 LOCAL ACTION GROUPS ADIC-HURDES CEDER DIVA ADISGATA CÁPARRA SOPRODEVAJEADICOVER ADESVAL ARJABOR The Extremadura Rural Development Network (REDEX) is a non- ADEME profit organisation composed of the 24 Local Action Groups of the TAGUS Autonomous Community of Extremadura. APRODERVI The Local Action Groups are regional non-profit associations in SIERRA DE ADICOMT SAN PEDRO which public and private entities are integrated to jointly work towards the LOS BALDÍOS social and economic development of their respective regions. ADISMONTA REDEX's scope of activity includes tourism development in rural ADECOM CEDER LA -
Iberian Lynx Conservation in Portugal
TILHE BERIAN YNX IN PORTUGAL STATUS SURVEY AND CONSERVATION ACTION PLAN ICN´ S LYNX MONITORING TEAM February 2004 I nstitutodaConservaçãodaNatureza -THE IBERIAN LYNX IN PORTUGAL- -Status Survey and Conservation Action Plan- Project coordinator: Pedro Sarmento – Reserva Natural da Serra da Malcata – Rua António Ribeiro Sanches 6090 Penamacor Portugal – e-mail: [email protected] Project Staff: Field Biologists: Pedro Monterroso – Parque Natural do Guadiana. Rua Dr. Afonso Costa, 40 1ª Dt, 7750-352 Mértola. E-mail: [email protected] Pedro Tarroso - Reserva Natural da Serra da Malcata – Rua António Ribeiro Sanches 6090 Penamacor Portugal – E-mail: [email protected] Catarina Ferreira – Parque Natural do Sudoeste Alentejano e Costa Vicentina. Rua Serpa Pinto, 32, 7630-174 Odemira. E-mail: [email protected] Nuno Negrões – Parque Nacional da Peneda-Gerês. Av. António Macedo, 4704-538 Braga. E- mail: [email protected] Luís Castro – Instituto da Conservação da Natureza/Divisão de Habitats e ecossistemas – Rua Filipe Folque, n.º 46 1150-144 Lisboa. Joana Cruz Reserva Natural da Serra da Malcata – Rua António Ribeiro Sanches 6090 Penamacor Portugal. E-mail: [email protected] Bruno Pinto- Instituto da Conservação da Natureza/Divisão de Habitats e ecossistemas – Rua Filipe Folque, n.º 46 1150-144 Lisboa. João Pargana – Parque Natural da Serra de S. Mamede. Rua General Conde de Avilez, 22 – 1º , 7300-185 Portalegre. E-mail. [email protected] Field assistents: José H. Fernandes, Francisco Campos, Nuno Cardoso, José Pires, António -

Catálogo De Medios
CATÁLOGO DE MEDIOS V.02 - 2018 BASES DE HELICÓPTEROS ZONAS DE COORDINACIÓN NOMBRE TÉRMINO MUNICIPAL HURDES PINOFRANQUEADO (BRIF) PINOFRANQUEADO AMBROZ – JERTE – TIETAR JARANDILLA JARANDILLA DE LA VERA GATA HOYOS HOYOS MONFRAGÜE SERRADILLA SERRADILLA VILLUERCAS – IBORES GUADALUPE GUADALUPE CÁCERES CENTRO BASE HALCÓN MALPARTIDA DE CÁCERES BASE VALENCIA SIERRA DE SAN PEDRO VALENCIA DE ALCÁNTARA ALCANTARA SIBERIA HERRERA DEL DUQUE HERRERA DEL DUQUE SERENA MANCHITA MANCHITA TENTUDIA BASE CALERA LEÓN CALERA DE LEÓN PUESTOS DE VIGILANCIA ZONAS DE COORDINACIÓN NOMBRE TÉRMINO MUNICIPAL HURDES AHYCEPO PINOFRANQUEADO HURDES COLGADIZO CAMINOMORISCO HURDES LA JINETA NUÑOMORAL HURDES LA VIÑUELA LADRILLAR AMBROZ – JERTE – TIETAR CERRO DE LAS CABEZAS JARAIZ DE LA VERA AMBROZ – JERTE – TIETAR TORNAVACAS TORNAVACAS AMBROZ – JERTE – TIETAR LA NAVA JARANDILLA DE LA VERA AMBROZ – JERTE – TIETAR MESALLANA VILLANUEVA DE LA VERA GATA AGACHADOS VALVERDE DEL FRESNO GATA CILLEROS CILLEROS GATA GATA GATA GATA ROBLEDILLO DE GATA ROBLEDILLO DE GATA GATA SIERRA DE DIOS PADRE VILLANUEVA DE LA SIERRA MONFRAGÜE LA SERRANA LA SERRANA MONFRAGÜE LAS CORCHUELAS TORREJÓN EL RUBIO MONFRAGÜE PICO DE MIRAVETE CASAS DE MIRAVETE MONFRAGÜE SANTA CATALINA SERRADILLA VILLUERCAS – IBORES CAMPILLO DE DELEITOSA CAMPILLO DE DELEITOSA VILLUERCAS – IBORES LA PALOMERA ALIA VILLUERCAS – IBORES PICO CERVALES NAVATRASIERRA VILLUERCAS – IBORES SIERRA DE CAÑAMERO CAÑAMERO CÁCERES CENTRO CERRO PEDRO GOMEZ HERGUIJUELA CÁCERES CENTRO EL ALJIBE ALISEDA PUERTOS DE LOS CÁCERES CENTRO CASAS DE MILLÁN -

Sin Título-1
+ info Megalithism Gastronomy Paths The berrea Birding We are surprised in the vicinity by a dolmen complex dating back to the Neolithic and Chalcolithic Period (4000-2500 Construction “Exploring BC). A unique legacy that we can today visit through of a dolmen signposted routes; those at Zafra, near Valencia de Alcántara; Mining of large el Mellizo, in Aceña de la Borrega; or at Tapada del Anta in 1 blocks of stone. La Raya“ Molino de la Negra route are some of the options available. Valencia de Alcántara m s Megalithic literally means "large stones", And Tajo Internacional and refers to those cultures who used them to Herrera de galithi build funerary monuments for thousands of e EX-374 Alcántara Transport using Cedillo Santiago de M years. As many as one hundred dolmens scattered 2 EX-376 Alcántara rollers. Megalithism Gastronomy CC-125 Carbajo around Valencia de Alcántara, Santiago de Alcántara, CC-37 Cedillo and Herrera de Alcántara, along with those present Paths The berrea Birding Membrío on the Portuguese side make up one of the most EX-374 important complexes of this type in all over Europe. 3 Placement of upright Salorino Herreruela stones and capstone. Valencia de N-521 Alcántara Marvão i CC-112 N-246-1 Aceña de la Borrega 4 Dolmen was covered with Introduction Dolmen Mellizo (Valencia de Alcántara) earth and smaller stones. This is the westernmost part of the province of Cáceres, a joint through which Amid quartzite clis and forests, the small farmsteads present along Extremadura delves into Portugal forming one of the emblematic surroundings of La Raya based their economy on smuggling until the removal of La Raya, a name which in local slang denotes the border between Spain and customs: La Fontañera, San Pedro, El Pino, Jola, Aceña de la Portugal as well as the areas nearby. -

Atlas De Los Paisajes De España: Extremadura OCUPACIÓN DEL
2.4.3 OCUPACIÓN DEL SUELO Y PAISAJE Atlas de los Paisajes de España: Extremadura 660.000 710.000 760.000 810.000 860.000 Castilla y León 15.04 15.03 5.01 15.02 15.01 40.01 15.06 5.04 48.10 50.01 40.04 50.02 .440.000 57.06 4 4.440.000 57.04 53.01 57.05 18.01 53.02 48.11 40.03 Castilla - 18.02 La Mancha 48.14 40.02 48.01 84.04 17.07 48.02 .380.000 4 48.13 4.380.000 48.12 17.08 78.04 48.33 78.05 18.07 18.03 48.03 46.05 53.05 48.16 25.01 18.04 17.09 18.08 46.06 48.15 18.06 PORTUGAL 78.06 48.17 53.03 57.01 48.18 48.17 53.04 18.05 18.09 .320.000 4 48.04 4.320.000 53.06 25.02 57.02 48.08 25.03 57.03 18.11 53.08 48.07 18.10 53.07 48.20 48.21 18.12 48.22 18.13 48.05 48.19 .260.000 4 48.06 4.260.000 48.25 53.10 48.26 53.09 Andalucía 48.31 27.08 48.27 27.08 27.01 48.29 48.30 48.28 27.02 27.02 48.37 48.37 010 20 40 Km 2 .200.000 4 4.200.000 660.000 710.000 760.000 810.000 860.000 Unidades del Paisaje Macizos Sistema Central Fosas y bordes S.Central Sierras cuarcíticas penillanura Corredores y valles intramontañas Páramos detríticos Meseta sur Sierras Sistema Central Gargantas y valles La Raya Sierras y valles extremeños Penillanuras sudoccidentales Vegas y cuencas Tajo-Guadiana Piedemonte S.Central Sierras Villuercas-Montes de Toledo Sierras y valles Sierra Morena Campiñas Meseta sur Fuente de datos: Atlas de los Paisajes de España: Extremadura. -

Iberian Red Deer
Iberian red deer: paraphyletic nature at mtDNA but nuclear markers support its genetic identity Juan Carranza1, Marıa Salinas1, Damian de Andres 1,2 & Javier Perez-Gonz alez 1 1Ungulate Research Unit, Catedra de Recursos Cinegeticos y Piscıcolas (CRCP), Universidad de Cordoba, 14071 Cordoba, Spain 2Instituto de Agrobiotecnologıa, CSIC-UPNA-Gobierno de Navarra, 31192 Mutilva, Navarra, Spain Keywords Abstract Cervus elaphus hispanicus, conservation genetics, Iberian glacial refugia, paraphyletic Red deer populations in the Iberian glacial refugium were the main source for taxa, phylogeny, phylogeography. postglacial recolonization and subspecific radiation in north-western Europe. However, the phylogenetic history of Iberian red deer (Cervus elaphus Correspondence hispanicus) and its relationships with northern European populations remain Juan Carranza, Ungulate Research Unit, uncertain. Here, we study DNA sequences at the mitochondrial control region Catedra de Recursos Cinegeticos y Piscıcolas along with STR markers for over 680 specimens from all the main red deer pop- (CRCP), Universidad de Cordoba, 14071 Cordoba, Spain. ulations in Spain and other west European areas. Our results from mitochon- Tel: 34 957 212025; drial and genomic DNA show contrasting patterns, likely related to the nature E-mail: [email protected] of these types of DNA markers and their specific processes of change over time. The results, taken together, bring support to two distinct, cryptic maternal lin- Funding Information eages for Iberian red deer that predated the last glacial maximum and that have This work was partly supported by project maintained geographically well differentiated until present. Haplotype relation- CGL2010-17163/BOS from the Spanish ships show that only one of them contributed to the northern postglacial recolo- MInistry of Science and by Extremadura and nization. -
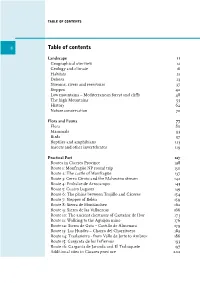
Table of Contents
TABLE OF CONTENTS 8 Table of contents Landscape 11 Geographical overview 12 Geology and climate 16 Habitats 21 Dehesa 23 Streams, rivers and reservoirs 37 Steppes 42 Low mountains – Mediterranean forest and cliffs 48 The high Mountains 55 History 62 Nature conservation 70 Flora and Fauna 77 Flora 80 Mammals 93 Birds 97 Reptiles and amphibians 113 Insects and other invertebrates 119 Practical Part 127 Routes in Cáceres Province 128 Route 1: Monfragüe NP round trip 130 Route 2: The castle of Monfragüe 137 Route 3: Cerro Gimio and the Malvecino stream 142 Route 4: Embalse de Arrocampo 145 Route 5: Cuatro Lugares 149 Route 6: The plains between Trujillo and Cáceres 154 Route 7: Steppes of Belén 159 Route 8: Sierra de Montánchez 162 Route 9: Sierra de las Villuercas 166 Route 10: The ancient chestnuts of Castañar de Ibor 173 Route 11: Walking to the Aguijón mine 176 Route 12: Sierra de Gata – Castillo de Almenara 179 Route 13: Las Hurdes – Chorro del Chorrituero 182 Route 14: Traslasierra - from Valle de Jerte to Ambroz 186 Route 15: Garganta de los Infiernos 193 Route 16: Garganta de Jaranda and El Trabuquete 197 Additional sites in Cácares province 202 TABLE OF CONTENTS 9 Badajoz Province 210 Route 17: A walk through Mérida 212 Route 18: Moheda Alta 216 Route 19: Sierra de San Pedro 219 Route 20: Sierra de Alor 222 Route 21: Between Zafra and Jerez de los Caballeros 225 Route 22: Sierra Grande de Hornachos 231 Route 23: The vast steppes of La Serena 235 Route 24: Benquerencia and the Sierra de Tiros 240 Additional sites in Badajoz Province