A Selective Overview of Sparse Principal Component Analysis
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Manchus: a Horse of a Different Color
History in the Making Volume 8 Article 7 January 2015 Manchus: A Horse of a Different Color Hannah Knight CSUSB Follow this and additional works at: https://scholarworks.lib.csusb.edu/history-in-the-making Part of the Asian History Commons Recommended Citation Knight, Hannah (2015) "Manchus: A Horse of a Different Color," History in the Making: Vol. 8 , Article 7. Available at: https://scholarworks.lib.csusb.edu/history-in-the-making/vol8/iss1/7 This Article is brought to you for free and open access by the History at CSUSB ScholarWorks. It has been accepted for inclusion in History in the Making by an authorized editor of CSUSB ScholarWorks. For more information, please contact [email protected]. Manchus: A Horse of a Different Color by Hannah Knight Abstract: The question of identity has been one of the biggest questions addressed to humanity. Whether in terms of a country, a group or an individual, the exact definition is almost as difficult to answer as to what constitutes a group. The Manchus, an ethnic group in China, also faced this dilemma. It was an issue that lasted throughout their entire time as rulers of the Qing Dynasty (1644- 1911) and thereafter. Though the guidelines and group characteristics changed throughout that period one aspect remained clear: they did not sinicize with the Chinese Culture. At the beginning of their rule, the Manchus implemented changes that would transform the appearance of China, bringing it closer to the identity that the world recognizes today. In the course of examining three time periods, 1644, 1911, and the 1930’s, this paper looks at the significant events of the period, the changing aspects, and the Manchus and the Qing Imperial Court’s relations with their greater Han Chinese subjects. -

This Is a Sample Copy, Not to Be Reproduced Or Sold
Startup Business Chinese: An Introductory Course for Professionals Textbook By Jane C. M. Kuo Cheng & Tsui Company, 2006 8.5 x 11, 390 pp. Paperback ISBN: 0887274749 Price: TBA THIS IS A SAMPLE COPY, NOT TO BE REPRODUCED OR SOLD This sample includes: Table of Contents; Preface; Introduction; Chapters 2 and 7 Please see Table of Contents for a listing of this book’s complete content. Please note that these pages are, as given, still in draft form, and are not meant to exactly reflect the final product. PUBLICATION DATE: September 2006 Workbook and audio CDs will also be available for this series. Samples of the Workbook will be available in August 2006. To purchase a copy of this book, please visit www.cheng-tsui.com. To request an exam copy of this book, please write [email protected]. Contents Tables and Figures xi Preface xiii Acknowledgments xv Introduction to the Chinese Language xvi Introduction to Numbers in Chinese xl Useful Expressions xlii List of Abbreviations xliv Unit 1 问好 Wènhǎo Greetings 1 Unit 1.1 Exchanging Names 2 Unit 1.2 Exchanging Greetings 11 Unit 2 介绍 Jièshào Introductions 23 Unit 2.1 Meeting the Company Manager 24 Unit 2.2 Getting to Know the Company Staff 34 Unit 3 家庭 Jiātíng Family 49 Unit 3.1 Marital Status and Family 50 Unit 3.2 Family Members and Relatives 64 Unit 4 公司 Gōngsī The Company 71 Unit 4.1 Company Type 72 Unit 4.2 Company Size 79 Unit 5 询问 Xúnwèn Inquiries 89 Unit 5.1 Inquiring about Someone’s Whereabouts 90 Unit 5.2 Inquiring after Someone’s Profession 101 Startup Business Chinese vii Unit -

Curriculum Vitae LEE
Curriculum Vitae LEE ZOU 1. General Information Primary Position: Associate Professor of Pathology Harvard Medical School Office Address: Massachusetts General Hospital Cancer Center Room 7404, Building 149, 13th Street Charlestown, MA 02129 Work email: [email protected] Work phone/fax: (617) 724-9534 / (617) 726-7808 2. Education and Training Education: 1999 Ph.D. Stony Brook University & Cold Spring Harbor Laboratory, New York (with Dr. Bruce Stillman, F.R.S.) 1994 M.S. Kansas State University, Kansas 1992 B.S. Sun Yet-Sen (Zhongshan) University, China Postdoctoral Training: 2000-2003 HMMI Associate/Postdoctoral Fellow (with Dr. Stephen Elledge) Department of Biochemistry Baylor College of Medicine (Named fellow, Damon Runyon Cancer Research Fund) 2003-2004 Research Fellow (with Dr. Stephen Elledge) Harvard Partners Center for Genetics and Genomics Brigham & Women’s Hospital/Harvard Medical School 3. Past and Current Positions 2004-2009 Assistant Professor of Pathology, Harvard Medical School 2004- Assistant Geneticist, Massachusetts General Hospital, Boston, MA 2004- Member, Massachusetts General Hospital Cancer Center 2005- Member, Ph.D. Program in Biological and Biomedical Science, Harvard Medical School 2006- Member, Dana-Farber/Harvard Cancer Center 2007- Member, Leder Human Biology and Translational Medicine Program, Harvard Medical School 2008- Assistant in Radiation Oncology, Massachusetts General Hospital 2009- Associate Professor of Pathology, Harvard Medical School 4. Honors and Awards 1998 Sigma Xi Award for Excellence in Research, Stony Brook University 1998 Abrahams Award for Outstanding Scientific Achievement by a Graduate Student, Stony Brook University 1998 Elected Associate Member, Sigma Xi, the Scientific Research Society 1999 The Harold Weintraub Graduate Student Award Nominee, Cold Spring Harbor Laboratory 2000 Fellow*, the Jane Coffin Child Memorial Fund for Medical Research 2000 Fayez Sarofim Fellow (named fellow), the Damon Runyon Cancer Research Fund 2001 The V. -

French Names Noeline Bridge
names collated:Chinese personal names and 100 surnames.qxd 29/09/2006 13:00 Page 8 The hundred surnames Pinyin Hanzi (simplified) Wade Giles Other forms Well-known names Pinyin Hanzi (simplified) Wade Giles Other forms Well-known names Zang Tsang Zang Lin Zhu Chu Gee Zhu Yuanzhang, Zhu Xi Zeng Tseng Tsang, Zeng Cai, Zeng Gong Zhu Chu Zhu Danian Dong, Zhu Chu Zhu Zhishan, Zhu Weihao Jeng Zhu Chu Zhu jin, Zhu Sheng Zha Cha Zha Yihuang, Zhuang Chuang Zhuang Zhou, Zhuang Zi Zha Shenxing Zhuansun Chuansun Zhuansun Shi Zhai Chai Zhai Jin, Zhai Shan Zhuge Chuko Zhuge Liang, Zhan Chan Zhan Ruoshui Zhuge Kongming Zhan Chan Chaim Zhan Xiyuan Zhuo Cho Zhuo Mao Zhang Chang Zhang Yuxi Zi Tzu Zi Rudao Zhang Chang Cheung, Zhang Heng, Ziche Tzuch’e Ziche Zhongxing Chiang Zhang Chunqiao Zong Tsung Tsung, Zong Xihua, Zhang Chang Zhang Shengyi, Dung Zong Yuanding Zhang Xuecheng Zongzheng Tsungcheng Zongzheng Zhensun Zhangsun Changsun Zhangsun Wuji Zou Tsou Zou Yang, Zou Liang, Zhao Chao Chew, Zhao Kuangyin, Zou Yan Chieu, Zhao Mingcheng Zu Tsu Zu Chongzhi Chiu Zuo Tso Zuo Si Zhen Chen Zhen Hui, Zhen Yong Zuoqiu Tsoch’iu Zuoqiu Ming Zheng Cheng Cheng, Zheng Qiao, Zheng He, Chung Zheng Banqiao The hundred surnames is one of the most popular reference Zhi Chih Zhi Dake, Zhi Shucai sources for the Han surnames. It was originally compiled by an Zhong Chung Zhong Heqing unknown author in the 10th century and later recompiled many Zhong Chung Zhong Shensi times. The current widely used version includes 503 surnames. Zhong Chung Zhong Sicheng, Zhong Xing The Pinyin index of the 503 Chinese surnames provides an access Zhongli Chungli Zhongli Zi to this great work for Western people. -

Strong Oracle Optimality of Folded Concave Penalized Estimation.” DOI:10.1214/13-AOS1198
The Annals of Statistics 2014, Vol. 42, No. 3, 819–849 DOI: 10.1214/13-AOS1198 c Institute of Mathematical Statistics, 2014 STRONG ORACLE OPTIMALITY OF FOLDED CONCAVE PENALIZED ESTIMATION By Jianqing Fan1, Lingzhou Xue2 and Hui Zou3 Princeton University, Pennsylvania State University and University of Minnesota Folded concave penalization methods have been shown to enjoy the strong oracle property for high-dimensional sparse estimation. However, a folded concave penalization problem usually has multiple local solutions and the oracle property is established only for one of the unknown local solutions. A challenging fundamental issue still remains that it is not clear whether the local optimum computed by a given optimization algorithm possesses those nice theoretical prop- erties. To close this important theoretical gap in over a decade, we provide a unified theory to show explicitly how to obtain the oracle solution via the local linear approximation algorithm. For a folded concave penalized estimation problem, we show that as long as the problem is localizable and the oracle estimator is well behaved, we can obtain the oracle estimator by using the one-step local linear approximation. In addition, once the oracle estimator is obtained, the local linear approximation algorithm converges, namely it pro- duces the same estimator in the next iteration. The general theory is demonstrated by using four classical sparse estimation problems, that is, sparse linear regression, sparse logistic regression, sparse precision matrix estimation and sparse quantile regression. 1. Introduction. Sparse estimation is at the center of the stage of high- dimensional statistical learning. The two mainstream methods are the LASSO (or ℓ1 penalization) and the folded concave penalization [Fan and Li (2001)] such as the SCAD and the MCP. -

The Linguistic Categorization of Deictic Direction in Chinese – with Reference to Japanese – Christine Lamarre
The linguistic categorization of deictic direction in Chinese – With reference to Japanese – Christine Lamarre To cite this version: Christine Lamarre. The linguistic categorization of deictic direction in Chinese – With reference to Japanese –. Dan XU. Space in Languages of China, Springer, pp.69-97, 2008, 978-1-4020-8320-4. hal-01382316 HAL Id: hal-01382316 https://hal-inalco.archives-ouvertes.fr/hal-01382316 Submitted on 16 Oct 2016 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Lamarre, Christine. 2008. The linguistic categorization of deictic direction in Chinese — With reference to Japanese. In Dan XU (ed.) Space in languages of China: Cross-linguistic, synchronic and diachronic perspectives. Berlin/Heidelberg/New York: Springer, pp.69-97. THE LINGUISTIC CATEGORIZATION OF DEICTIC DIRECTION IN CHINESE —— WITH REFERENCE TO JAPANESE —— Christine Lamarre, University of Tokyo Abstract This paper discusses the linguistic categorization of deictic direction in Mandarin Chinese, with reference to Japanese. It focuses on the following question: to what extent should the prevalent bimorphemic (nondeictic + deictic) structure of Chinese directionals be linked to its typological features as a satellite-framed language? We know from other satellite-framed languages such as English, Hungarian, and Russian that this feature is not necessarily directly connected to satellite-framed patterns. -

XUE ZHI ZOU, Petitioner V
Case: 12-4266 Document: 003111240337 Page: 1 Date Filed: 04/25/2013 NOT PRECEDENTIAL UNITED STATES COURT OF APPEALS FOR THE THIRD CIRCUIT ___________ No. 12-4266 ___________ XUE ZHI ZOU, Petitioner v. ATTORNEY GENERAL OF THE UNITED STATES, Respondent ____________________________________ On Petition for Review of an Order of the Board of Immigration Appeals (Agency No. A079-092-389) Immigration Judge: Honorable Susan G. Roy ____________________________________ Submitted Pursuant to Third Circuit LAR 34.1(a) April 24, 2013 Before: AMBRO, JORDAN and BARRY, Circuit Judges (Opinion filed: April 25, 2013) ___________ OPINION ___________ PER CURIAM Petitioner Xue Zhi Zou seeks review of a final order of the Board of Immigration Appeals (“BIA”). For the following reasons, we will deny the petition for review. Petitioner, a citizen of the People’s Republic of China, arrived in the United States in 2001. Removal proceedings were initiated against him under INA § 212(a)(6)(A)(i); 8 Case: 12-4266 Document: 003111240337 Page: 2 Date Filed: 04/25/2013 U.S.C. § 1182(a)(6)(A)(i), as an alien present in the United States without being admitted or paroled. Petitioner conceded removability, but applied for asylum, withholding of removal, and protection under the Convention Against Torture, based on his practice of Falun Gong. The Immigration Judge (“IJ”) denied relief, finding no past persecution or well-founded fear of future persecution, and ordered Petitioner removed to China. On July 25, 2011, the BIA upheld the IJ’s decision. On October 17, 2011, Petitioner filed a timely motion to reopen, arguing that he had recently converted to Catholicism and feared persecution on that basis if returned to China. -
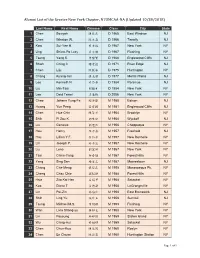
Alumni List of the Greater New York Chapter, NTUMCAA-NA (Updated 10/30/2018)
Alumni List of the Greater New York Chapter, NTUMCAA-NA (Updated 10/30/2018) Last Name First Name Chinese Class City State 1 Chen Sowyeh 陳授業 D 1965 East Windsor NJ 2 Chen Winston W. 陳⽂忠 D 1966 Tenafly NJ 3 Kow Sui-Yee H. ⿈秀逸 D 1967 New York NY 4 Ung Shiaw-Po Lucy 李⼩勃 D 1967 Flushing NY 5 Tseng Yang S. 曾陽賢 D 1968 Englewood Cliffs NJ 6 Shieh Ching C. 謝⾦權 D 1971 River Edge NJ 7 Chen Liju 陳麗珠 D 1975 Huntington NY 8 Chang Kuang-min 張光敏 D 1977 Morris Plains NJ 9 Lee Kenneth N. 李乃恭 D 1984 Paramus NJ 10 Liu Min-Tsai 劉敏才 D 1984 New York NY 11 Lee Daid Tawei 李達維 D 2006 New York NY 12 Chao Johann Yung-Fa 趙榮發 M 1950 Edison NJ 13 Huang Yun Peng ⿈雲鵬 M 1951 Englewood Cliffs NJ 14 Chen Hua-Chin 陳華琴 M 1954 Brooklyn NY 15 Shih Pi Zou K. 郭璧如 M 1954 Wyckoff NJ 16 Liu Genesia 劉瑾熙 M 1956 Chappaqua NY 17 Hou Henry 侯宗泰 M 1957 Freehold NJ 18 Hsu Lillian Y.F. 徐裕芬 M 1957 New Rochelle NY 19 Lin Joseph P. 林本芝 M 1957 New Rochelle NY 20 Liu Lena 劉麗娜 M 1957 New York NY 21 Tsai Chhin-Yang 蔡青陽 M 1957 Forest Hills NY 22 Yang Sing San 楊省三 M 1957 Moorestown NJ 23 Chang Che-Meng 張哲孟 M 1958 Massapequa Pk. NY 24 Cheng Chau Chie 鄭昭傑 M 1958 Forest Hills NY 25 Hsia Zita Kai Hen 夏開亨 M 1958 Setauket NY 26 Kao Diana T. -

The Case of Wang Wei (Ca
_full_journalsubtitle: International Journal of Chinese Studies/Revue Internationale de Sinologie _full_abbrevjournaltitle: TPAO _full_ppubnumber: ISSN 0082-5433 (print version) _full_epubnumber: ISSN 1568-5322 (online version) _full_issue: 5-6_full_issuetitle: 0 _full_alt_author_running_head (neem stramien J2 voor dit article en vul alleen 0 in hierna): Sufeng Xu _full_alt_articletitle_deel (kopregel rechts, hier invullen): The Courtesan as Famous Scholar _full_is_advance_article: 0 _full_article_language: en indien anders: engelse articletitle: 0 _full_alt_articletitle_toc: 0 T’OUNG PAO The Courtesan as Famous Scholar T’oung Pao 105 (2019) 587-630 www.brill.com/tpao 587 The Courtesan as Famous Scholar: The Case of Wang Wei (ca. 1598-ca. 1647) Sufeng Xu University of Ottawa Recent scholarship has paid special attention to late Ming courtesans as a social and cultural phenomenon. Scholars have rediscovered the many roles that courtesans played and recognized their significance in the creation of a unique cultural atmosphere in the late Ming literati world.1 However, there has been a tendency to situate the flourishing of late Ming courtesan culture within the mainstream Confucian tradition, assuming that “the late Ming courtesan” continued to be “integral to the operation of the civil-service examination, the process that re- produced the empire’s political and cultural elites,” as was the case in earlier dynasties, such as the Tang.2 This assumption has suggested a division between the world of the Chinese courtesan whose primary clientele continued to be constituted by scholar-officials until the eight- eenth century and that of her Japanese counterpart whose rise in the mid- seventeenth century was due to the decline of elitist samurai- 1) For important studies on late Ming high courtesan culture, see Kang-i Sun Chang, The Late Ming Poet Ch’en Tzu-lung: Crises of Love and Loyalism (New Haven: Yale Univ. -

2020 Annual Report
2020 ANNUAL REPORT About IHV The Institute of Human Virology (IHV) is the first center in the United States—perhaps the world— to combine the disciplines of basic science, epidemiology and clinical research in a concerted effort to speed the discovery of diagnostics and therapeutics for a wide variety of chronic and deadly viral and immune disorders—most notably HIV, the cause of AIDS. Formed in 1996 as a partnership between the State of Maryland, the City of Baltimore, the University System of Maryland and the University of Maryland Medical System, IHV is an institute of the University of Maryland School of Medicine and is home to some of the most globally-recognized and world- renowned experts in the field of human virology. IHV was co-founded by Robert Gallo, MD, director of the of the IHV, William Blattner, MD, retired since 2016 and formerly associate director of the IHV and director of IHV’s Division of Epidemiology and Prevention and Robert Redfield, MD, resigned in March 2018 to become director of the U.S. Centers for Disease Control and Prevention (CDC) and formerly associate director of the IHV and director of IHV’s Division of Clinical Care and Research. In addition to the two Divisions mentioned, IHV is also comprised of the Infectious Agents and Cancer Division, Vaccine Research Division, Immunotherapy Division, a Center for International Health, Education & Biosecurity, and four Scientific Core Facilities. The Institute, with its various laboratory and patient care facilities, is uniquely housed in a 250,000-square-foot building located in the center of Baltimore and our nation’s HIV/AIDS pandemic. -

Shouzhong Zou
Curriculum Vitae Shouzhong Zou Contact Department of Chemistry, American University, Washington, DC 20016 Phone: 202-885 1763 (Office), 513-523 8860 (cell) E-mail: [email protected] Research Interests 1. Electrocatalysis: synthesis and characterization of size, shape and composition controlled metal nanocrystals; carbon-based catalysts for ORR and CO2 reduction; single particle electrochemistry and spectroscopy; polymer electrolyte membrane fuel cells; electroreduction of CO2; gas sensing 2. Surface vibration spectroscopy: surface-enhanced Raman and infrared spectroscopies; SiO2-Au core-shell nanoparticles, supported lipid membranes Education 1999 Ph.D. in Chemistry, Purdue University (with Dr. Michael J. Weaver) 1994 M.S. in Chemistry, Xiamen University (with Dr. Zhong-Qun Tian) 1991 B.S. in Chemistry, Xiamen University, China Professional Appointments 08/2015 – present Professor & Chair, Department of Chemistry, American University 01/2015 – 06/2015 Research Chemist, Joint Pathology Center (on leave from Miami University) 08/2008 – 07/2015 Associate Professor, Department of Chemistry and Biochemistry, Miami University (on leave 01/2015- 07/2015) 08/2002 – 07/2008 Assistant Professor, Department of Chemistry and Biochemistry, Miami University 10/1999 – 07/2002 Postdoctoral Scholar, Division of Chemistry and Chemical Engineering, California Institute of Technology (with Drs. Fred C. Anson & Ahmed H. Zewail) Honors and Awards Senior Visiting Scholar, Fudan University, Shanghai, China (2012-2014) Lilly Graduate Fellowship (1998-99) Reilley Upjohn Award in Analytical Chemistry (1998) Energy Research Summer Fellowship of the Electrochemical Society (1998) Guanghua Award, Xiamen University, China (1992) Bailin Award, Xiamen University, China (1991) Professional Societies American Chemical Society Electrochemical Society Society for Electroanalytical Chemistry International Society of Electrochemistry External Research Grants 12. -

Origin Narratives: Reading and Reverence in Late-Ming China
Origin Narratives: Reading and Reverence in Late-Ming China Noga Ganany Submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the Graduate School of Arts and Sciences COLUMBIA UNIVERSITY 2018 © 2018 Noga Ganany All rights reserved ABSTRACT Origin Narratives: Reading and Reverence in Late Ming China Noga Ganany In this dissertation, I examine a genre of commercially-published, illustrated hagiographical books. Recounting the life stories of some of China’s most beloved cultural icons, from Confucius to Guanyin, I term these hagiographical books “origin narratives” (chushen zhuan 出身傳). Weaving a plethora of legends and ritual traditions into the new “vernacular” xiaoshuo format, origin narratives offered comprehensive portrayals of gods, sages, and immortals in narrative form, and were marketed to a general, lay readership. Their narratives were often accompanied by additional materials (or “paratexts”), such as worship manuals, advertisements for temples, and messages from the gods themselves, that reveal the intimate connection of these books to contemporaneous cultic reverence of their protagonists. The content and composition of origin narratives reflect the extensive range of possibilities of late-Ming xiaoshuo narrative writing, challenging our understanding of reading. I argue that origin narratives functioned as entertaining and informative encyclopedic sourcebooks that consolidated all knowledge about their protagonists, from their hagiographies to their ritual traditions. Origin narratives also alert us to the hagiographical substrate in late-imperial literature and religious practice, wherein widely-revered figures played multiple roles in the culture. The reverence of these cultural icons was constructed through the relationship between what I call the Three Ps: their personas (and life stories), the practices surrounding their lore, and the places associated with them (or “sacred geographies”).