DOCSLIB.ORG

Crystal Structure, Hydrogen Bonding and Relations with Haidingerite And

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Crystal Structure, Hydrogen Bonding and Relations with Haidingerite And American Mineralogist, Volume 64, pages 1248-1254, 1979 Krautite, Mn(HTOXAsOTOH):crystal structure, hydrogenbonding and relations with haidingeriteand pharmacolite MICHELE Cern .a.No MnRnnLLa FnINcHINI-ANGELA Istituto di Mineralogia, Cristallografia e Geochimica "G. Spezia" Universitd di Torino, Via S. Massimo 22, 10123 Torino, Italy Abstract The crystal structure of synthetic krautite was solved (direct methods) and refined isotrop- ically (R:0.112) in spacegroup P2, with2294 reflectionsmeasured on a single-crystaldif- fractometer,with MoKc radiation. The unit-cell parametersate: a :8.012(2), b: 15.956@, c : 6.801(2)A,P : 96.60(3)";Z :8. A strong F2r/n pseudosymmetryappears in the struc- ture, yet the averagepseudo-center is slightly shifted from the correct position l/4,0, l/4 n spacegroup Y2r/n."Ihe structureis built up by (010)layers of AsO_oand MnOu coordination polyhedra.In eachlayer, MnOu octahedrashare edges to form [0Tl chahs, which sandwich the AsOotetrahedra. Adjacent layers are related by the screwaxis and are linked by four out of twelve independenthydrogen bonds; two of them are acidic and two are donatedby water molecules. One of the latter hydrogen bonds is probably bifurcated, since the water molecule is involved in two contacts2.92arLd 3.08A long. Haidingerite (CaHAsOo'HrO) and pharma- colite (CaHAsOo. 2HzO) show similar structuresformed by layersof coordination polyhedra connectedby hydrogenbonds. For 11e5ingle-layer topology, krautite resemblespharmacolite (chain-like structure) more than haidingerite (network-like structure), since the increase of coordination number from Mn2* to Ca2* is compensatedby the increaseof water content. Introduction strong mica-tke (010) cleavages,so that analogous structure types seemappropriate, in spite of In a seriesof structural and crystal-chemicalinves- layered the fact that the symmetries are different (rronoclinic tigations on mineral arsenatescontaining hydrogen for krautite and orthorhombic for haidingerite), and bonds (Catti et al., 1977), the manganesearsenate important differences appear in their X-ray powder krautite, recently described and characterized as a patterns. new mineral by Fontan et al. (1975),has been exam- ined. The other known natural manganesearsenates Experimental are a large group of basic arsenates(Moore, 1967), manganesehoernesite (Mn, Mg)r(AsOo)r' 8HrO, and Since good quality single crystals could not be the new mineral CaMn(HAsO)r'ZIJ.,O (Permingeat found in the natural samplesof krautite (Fontan et et al., in preparation). The synthetic crystalline al., 1975),synthetic crystalline MnHAsOo' HrO was phases reported in the system MnO-As'Or-HrO prepared. By mixing aqueoussolutions of MnCL and (Pascal,1966, p. 923) are Mnr(AsOo),'HrO, KHrAsOo a transparent gel was obtained (Deiss, MnHAsOo' HrO, Mn(HrAsOo)', Mn(HrAsOn)t l9l4), from which many small pink balls (about 2 .3H"O, and MnHAsOo'4HrO; the last compound mm diameter) precipitated;each ball was formed by is probably isomorphous with brassite, MgHAsOn tiny, crystalline packets of MnHAsOo'H'O. Every .4H2O, the structure of which is known (Protas packet contained very thin {010} lamellae,with fre- and Gindt, 1976). Krautite is the first acid man- quent polysynthetic twinning. With great difficulty ganousarsenate studied structurally; we aim to clar- an irregular crystalline fragment 0.30 x 0.10 x 0.02 ify the crystal-chemical relationships with its calcium mm could be isolated,and was usedfor all measure- homolog haidingerite, CaHAsOo'HrO (Cassien et ments. al., 1966:'Calleri and Ferraris, 1967).Indeed, both By meansof Weissenbergphotographs and single- minerals show very similar cell parameters and crystal diffractometry the monoclinic unit cell offi3-{oax / 79 / I I l 2- l 248$02.00 1248 CATTI AND FRANCHINI-ANGEL/I: KRAUTITE 1249 reported by Fontan et al. was confirmed. The least- Table l. Atomic fractional coordinates and thermal parameters squaresrefinement of 25 0 valuesmeasured on a dif- (A'?) fractometer [tr(MoKa) : 0.71069A]yielded the unit- cell parameters a : 8.012(2), b : 15.956(4),c : 6.801(2)4,B :96.60(3)". Othercrystal data are:V : 863.7A',Z:8, M :212.879,p (meas): 3.30g cm-, Mn(1) 0.4033(4)1' 0.0451(z) 0 .6520\4) 0 .69(4) : Mn(l') 0 . I 069(4) -0 .0455(2 ) 0.9043(4) 0.16\41 (Fontan et al.,1975),p (calc) 3.274g cf,-', f(000) Mn(2) 0.8581 (4) 0 .0663(2) 0.r631(4) 0.71(4) : I128,p(MoKc) : .l I1.7 cm-'. On the basisof sys- I"ln(2') o.65ll(4) -0.0661(2) 0 .393414) o .70(4) tematic absences,the spacegroup could be either p2, As(1) o,4087\Z) 0 .0874(r ) 0.1473(3) 0.61(3) or FZ,/m; an analysis of statistical tests on the dif- As(l') o. l ooo(2) -0.0881(1) 0.4075(3) 0.57(3) As(z) 0.8140(2) 0.r014(r) 0.6689(3) 0.52(3) fraction intensities to detect the symmetry center As(2') o.6976\2) -0.r035(r) 0.8891(3) 0.52(3) gave ambiguousresults. o(l ) o.297 (z) 0.17r(r) o.zoz\z) r.l(2) The intensities were measuredon a Philips PW o(t') 0.zlrlz) -0.r69(1) 0.35r(2) 1.1(2) -o ll00 automatic four-circle diffractometer with the o(2) o.329\2) 0 .036(I ) .054\zl o.7(z) o(2') o. r 83(2) -0 .036(r ) o.612\21 1.o(z) following conditions: MoKa radiation, graphite o(3) o.449\ZJ 0.023(r) o.342\ZJ 0.9(2) monochromator,0 = 30", o, scan,A<.r : 1.40o,scan- o(3') 0.058(1) -0 .022(I ) o.zr4\z) 0.3(z) ning o(4) 0.603(z) 0 129(1) o.092\?.\ r.3(2) speed0.04o s-', backgroundtime 5 secon both oi4') -0 .()90(z) -o.r29(r) 0.462(2) O.7\Z) sidesof each peak, attenuatingfilter inserted for in- o( 5) 0.624121 0.134(1) o.1r7(zl 1.1(2) tensitieshigher than 60000counts s-', three reference o(5') 0.888(2) -0.133(r) 0.84r(z) o.7lz) reflections.By removing the reflectionswith = o(6) 0.916(z) 0 .050{I ) 0.862(2) o.7(z) l.F"l o(6') 0.593\Z) -0.0510) o.696(2) o.9(2) 3o(lF"l),2294 independentobservations remained for o(7) 0.808(2) o .044(l ) 0.462(z) 1.0(2) this study.' o(7') 0.1 07 (zl -0 .045(r ) | .097(2) 0.9(2) o(8) 0.938(z) 0.189(1) o.644(2) l .4(2) Solution and refinementof the structure o(8') 0.583(Z) -0.190(r) o.922(3) I .6(3) w(r) 0.264lz) 0.164(l) 0.583(2) r.5(2) The program MulreN based on direct methods w(l') o.248\2) -0.166(1) 0.964(2) r.4lz) (Germain et al., l97l) was usedto solvethe structure. w(2) o.960\2) 0.r90(r) 0.168(3) r.8(3) \4(2') o,545\2) -0.187( l ) 0.391(3) 1.8(3) In the centrosymmetricalspace group Y2,/m only pseudo-solutionswere obtained; the correct solution Estimated standard deviations are given in Parentheses and refer was found in the non-centrosymmetricalspace group to the last decimal place. P2,, showing the positions of the four As and four Mn independentatoms. By subsequentstructure-fac- tor calculationsand Fourier differencemaps, all the severalatoms becamenon-positive-definite. No ab- oxygen atoms were located. The full-matrix least- sorption correction could be performed,owing to the squaresrefinement with isotropictemperature factors irregularity of the crystalline fragment; this must for all atoms converged : to R 0.112;anomalous have introduced large systematicerrors into the data, scatteringof As and Mn atoms was correctedfor. and becauseof the lamellar shape of the crystal and of y the coordinate of As(l)'z was locked during the re- the large value of the linear absorption coefficient, finement to fix the origin. The following weighting and would account for the failure of the anisotropic schemewas used: w: l/(5 x lO-4l,ql,+ l); then the refinement. Table I reports the final atomic frac- averagevalues groups of 42 for of reflections were tional coordinates;large values of the e.s.d.'scan be practically constant.An anisotropic refinement was observedand could be ascribedto the pseudo-sym- tried unsuccessfully, since the temperature factors of metry of the structure (cf. the discussion), which causesa high correlation between atomic positional I To receive a copy of the structure factor table, order parameters in the refinement. Document AM-79-ll3 from the BusinessOffice, Mineralogical Society of America, 2000 Florida Avenue, NW, Washington, D. Discussion C. 20009.Please remit $1.00in advancefor the microfiche. 2 A single figure in parentheses denotes an atom of the Pseudo-symmetryand descriptionof the structare asymmetric unit; primed figures mean the pseudo-symmetry A strong PZ,/n pseudo-symmetryis shown by in- operation l/2 - x, r, | /2 - z. The secondfigure 2 is included for atoms in the equivalent position 7, l/2 + y, Z Roman numerals spection of Table l. All atoms can be grouped in representthe following translations:I, -c; II, +c; III, -a; IV, +a; pairs related by a pseudo-centerof inversion, which - V, +a b + c; VI, +r + c; VII, +2a + c. is located on the averageat x : 0.2555,! : O, 2 : 1250 CATTI AND FRANCHINI-ANGEI.A: KRAUTITE 'table 2. Interatomic distances and O-As-O angles in the four Table 3. Interatomic distances and O-Mn-O angles in the Mn independent AsOa groups coordination Polyhedra Mn(I')- o(Z'i 2.r5(r)i As(l)- o(l) l .67(2) A As(l')- o(1') t.64\2)A Mn(l) o(Z)II 2.15(r)A - - As(1.) o(2) r.65(r) As(lr) o(2') r.69(r) Nln(l)- o(3) z.2l(l) Mn(1')- o(3')II z.zz\t ) As(l) - o(3) L67(l ) As(1')_ o(3r) r.69(t) Mn(1 ') o(2)II z.zo(r) As(l) - o(4) r.7'7(Z) As(l')- o(4r) r.73(r) Mn(I ) O(2') 2.18(l ) '1 Aver a8e t.69 Average I .69 N{n(1)- O(5) 2.28\Z) ,,n11 - ois')III z,24\r ) z.l5(1) tr{,(1,)- 6161III z.r6(l) es(z) o(5) I .68(2) As(2')- o(5') r.66(l) Nln(l)- o(6') Asiz)- o(6) L 68(1) As(2')- 0(6') i.700) Mn(r) w(1) 2,22t2) Mn(1')- w(1') z.z4\z) As(2)- O{7) I .68(2) As(2')- o(7') 1.69U ) AVera gc z.z0 Average z.z0 As(2)- o(8) | .'t3\z) As(2')- O(8') 1.69(2) Average 1,69 Average I .69 .IV Mn(Z)- O(4) z.z1\z) f4n(2') O(4') 2,30(l) o(r)...o(z)2,?9A t14.3" o(1,)...o(2')2.79A 114,0" - ou).
Load more

Recommended publications
  • Profesionální Referát
    Journal of the Czech Geological Society, 42/4 (1997) 115 History of secondary minerals discovered in Jáchymov (Joachimsthal) Historie objevů sekundárních minerálů z Jáchymova (Czech summary) FRANTIŠEK VESELOVSKÝ1 - PETR ONDRUŠ1 - JAN HLOUŠEK2 1 Czech Geological Survey, Klárov 3, 118 21 Prague 1 2 U Roháčových kasáren 24, 110 00 Prague 10 Jáchymov is type locality for 22 minerals, including 17 secondary minerals. Data on history of discovery and description of new minerals was extracted by search in old literature. Minerals are arranged in the chronological sequence of discovery. Explanation of names of discredited or re-defined minerals and some historical names is included at the end of this paper. Key words: secondary minerals, history description, old mineral names, Jáchymov Introduction This work was continued a decade later by Schrauf. Larsen extensively studied the optical properties of Mining in Jáchymov experienced episodes of boom as Jáchymov minerals at the beginning of the twentieth well as periods of severe decline. Its prosperity was de- century.R. Nováček (1935-1941) studied in detail mainly pendent of mineral wealth and during ages the main secondary minerals from Jáchymov. X-ray diffraction, interest moved from silver to uranium ores. Mineralogy, widely introduced after 1945, provided a new powerful mining and ore dressing proved to be often mutually method of mineral identification. Frondel and Peacock interdependent. The beginnings of mineralogy in Jáchy- continued study of Jáchymov minerals. But only mu- mov date to mining development in early 16th century. seum specimens were available by that time. The first mineralogical notes appear in texts by Agricola The secrecy surrounding uranium mining in the pe- [86], Mathesius, Ercker, and others.
    [Show full text]
  • Distribution of As, Ni and Co in Tailings and Surface Waters in the Cobalt Area, Ontario1
    DISTRIBUTION OF AS, NI AND CO IN TAILINGS AND SURFACE 1 WATERS IN THE COBALT AREA, ONTARIO Jeanne B. Percival2, Y.T. John Kwong3, Charles G. Dumaresq4, Frederick A. Michel5 Abstract: From 1904 until the mid 1930’s and intermittently until 1989, over 450 million troy ounces of silver was mined from the Cobalt area, Ontario. Currently there is no active mining of silver, but the area has seen recent exploration activities for other commodities such as diamonds. Cobalt, however, has not only a renowned mining history, but also an environmental legacy. The area is characterized by remnant historic mine workings and numerous waste rock piles and tailings ponds. Several elements of concern including arsenic, nickel and cobalt continually enter the local watershed from the tailings and waste rock piles. These elements are transported through surface waters to the wetlands in the Farr Creek drainage basin and ultimately enter Lake Timiskaming. Tailings samples are composed of abundant plagioclase with subordinate quartz, chlorite, calcite and dolomite. Less common are K-feldspar, amphibole and mica as well as trace minerals such as erythrite, scorodite and pharmocolite. When efflorescent mineral crusts form on tailings surfaces they are dominated by either gypsum or thenardite. The tailings may contain up to 3.5 wt % Co and 2.2 wt% Ni. Lake sediment and tailings cores show concentrations up to 1.8 wt% As, 0.62 wt% Co and 0.27 wt% Ni in the solids, and 160 mg/L As, 74 mg/L Co and 42 mg/L Ni in the pore waters. One core collected from the infilled Hebert Pond situated within the Nipissing Low Grade Mill tailings impoundment show pore water concentrations in excess of 1,500 mg/L As associated with an organic- rich layer.
    [Show full text]
  • Geologica Macedonica
    UDC 55 In print: ISSN 0352–1206 CODEN – GEOME 2 On line: ISSN 1857–8586 GEOLOGICA MACEDONICA Geologica Macedonica Vol. No pp. Štip 2 91–176 2018 Geologica Macedonica Год. 32 Број стр. Штип Geologica Macedonica Vol. No pp. Štip 2 91–176 2018 Geologica Macedonica Год. 32 Број стр. Штип GEOLOGICA MACEDONICA Published by: – Издава: "Goce Delčev" University in Štip, Faculty of Natural and Technical Sciences, Štip, Republic of Macedonia Универзитет „Гоце Делчев“ во Штип, Факултет за природни и технички науки, Штип, Република Македонија EDITORIAL BOARD Todor Serafimovski (R. Macedonia, Editor in Chief), Blažo Boev (R. Macedonia, Editor), David Alderton (UK), Tadej Dolenec (R. Slovenia), Ivan Zagorchev (R. Bulgaria), Wolfgang Todt (Germany), Nikolay S. Bortnikov (Russia), Clark Burchfiel (USA), Thierry Augé (France), Todor Delipetrov (R. Macedonia), Vlado Bermanec (Croatia), Milorad Jovanovski (R. Macedonia), Spomenko Mihajlović (Serbia), Dragan Milovanović (Serbia), Dejan Prelević (Germany), Albrecht von Quadt (Switzerland) УРЕДУВАЧКИ ОДБОР Тодор Серафимовски (Р. Македонија, главен уредник), Блажо Боев (Р. Македонија, уредник), Дејвид Олдертон (В. Британија), Тадеј Доленец (Р. Словенија), Иван Загорчев (Р. Бугарија), Волфганг Тод (Германија), акад. Николај С. Бортников (Русија), Кларк Барчфил (САД), Тиери Оже (Франција), Тодор Делипетров (Р. Македонија), Владо Берманец (Хрватска), Милорад Јовановски (Р. Македонија), Споменко Михајловиќ (Србија), Драган Миловановиќ (Србија), Дејан Прелевиќ (Германија), Албрехт фон Квад (Швајцарија) Language editor Лектура Marijana Kroteva Маријана Кротева (English) (англиски) Georgi Georgievski Георги Георгиевски (Macedonian) (македонски) Technical editor Технички уредник Blagoja Bogatinoski Благоја Богатиноски Proof-reader Коректор Alena Georgievska Алена Георгиевска Address Адреса GEOLOGICA MACEDONICA GEOLOGICA MACEDONICA EDITORIAL BOARD РЕДАКЦИЈА Faculty of Natural and Technical Sciences Факултет за природни и технички науки P.
    [Show full text]
  • Download Download
    338 Geologica Macedonica, Vol. 32, No. 2, pp. 95–117 (2018) GEOME 2 IISSN 0352 – 1206 Manuscript received: August 5, 2018 e-ISSN 1857 – 8586 Accepted: November 7, 2018 UDC: 553.46:550.43.08]:504(497.721) 553.497:550.43.08]:504(497.721) Original scientific paper SUPERGENE MINERALOGY OF THE LOJANE Sb-As-Cr DEPOSIT, REPUBLIC OF MACEDONIA: TRACING THE MOBILIZATION OF TOXIC METALS Uwe Kolitsch1,2, Tamara Đorđević2, Goran Tasev3, Todor Serafimovski3, Ivan Boev3, Blažo Boev3 1Mineralogisch-Petrographische Abt., Naturhistorisches Museum, Burgring 7, A-1010 Wien, Austria 2Institut für Mineralogie und Kristallographie, Universität Wien, Althanstr. 14, A-1090 Wien, Austria 3Department of Mineral Deposits, Faculty of Natural and Technical Sciences, “Goce Delčev” University in Štip, Blvd. Goce Delčev 89, 2000 Štip, Republic of Macedonia [email protected] A b s t r a c t: As part of a larger project on the environmental mineralogy and geochemistry of the Lojane Sb- As-Cr deposit, Republic of Macedonia, which was mined for chromite and, later, stibnite until 1979 and is a substantial source of arsenic and antimony pollution, the supergene mineralogy of the deposit was studied. Samples collected on ore and waste dumps were used to identify and characterize the previously uninvestigated suite of supergene mineral phases by standard mineralogical techniques. The following species were determined (in alphabetical order): annaber- gite, arseniosiderite(?), gypsum, hexahydrite, hörnesite, pararealgar, roméite-group minerals, rozenite, scorodite, sen- armontite, stibiconite, sulphur, tripuhyite and valentinite. Their occurrences are described and their local conditions of formation are discussed. High-resolution Raman spectra of hörnesite, hexahydrite and rozenite are provided and com- pared with literature data.
    [Show full text]
  • MINERALS with a FRENCH CONNECTION François Fontan and Robert F
    MINERALS with a FRENCH CONNECTION François Fontan and Robert F. Martin The Canadian Mineralogist Special Publication 13 TABLE OF CONTENTS Préface vii Preface viii Introduction 1 The scope and contents of this book 1 Early discoveries 1 The three museums in Paris 2 Previous surveys of minerals discovered in France 5 The profile of mineralogy in France today 6 The information to be reported in each entry 6 Bibliography 7 Acknowledgements: special mentions 8 Acknowledgements prepared by François Fontan (2005–2007) 9 Acknowledgements prepared by Robert F. Martin (2007–2017) 9 Hold the presses: new arrivals! 11 Minerals with a type locality in France 13 Minerals discovered elsewhere and named after French citizens 267 Six irregular cases 525 Appendices and indexes 539 The appendices 540 Appendix 1. Minerals with a type locality in France, including New Caledonia: alphabetical listing 541 Appendix 2. Minerals (n = 127) with a type locality in France, including New Caledonia: chronological listing 544 Figure A1. Geographic distribution of mineral discoveries in France 545 Figure A2. Geographic distribution of mineral discoveries in New Caledonia 546 Figure A3. The number of type localities of minerals, grouped by decade 546 Appendix 3. Minerals with a type locality in France, including New Caledonia: geographic distribution 547 Appendix 4. Minerals discovered elsewhere than in France and named after French citizens: alphabetical list 549 Appendix 5. Minerals (n = 128) discovered elsewhere than in France and named after French citizens: chronological listing 552 Appendix 6. Minerals discovered elsewhere than in France and named after French citizens: geographic distribution 553 Appendix 7. The top 21 countries ranked according to the number of new mineral species discovered 556 Appendix 8.
    [Show full text]
  • New Mineral Names*
    The American Mineralogist, Volume60, pages945-947, l9Z5 NEW MINERAL NAMES* Mlcttnrl FLerscurn AND J. A. MnuonRrNo Brassite* The mineral,associated with realgar,native As, and a little orpi- FneNcors FoNTAN,Mencsl Onlrnc, FnnNcors prnurNcrer, ment,occurs as grains up to 0.2mm in calciteveinlets in marlsand RoleNo Prrnnor, nNo RsleNr Sre,nr_(1973) La brassite, siliceouslimestones at Duranus,Alpes-Maritimes, France. MgHAsO..4HrO. Bull. Soc. Franc. Mineral. Cristallogr. 96, The nameis for the locality.Type materialis at the EcoleNatl. 365-370. Superieuredes Mines, Paris.M.F. Analysisby M.O. on 15.4mg from Jachymovgave AsrOr 4g.1, Jagowerite* MgO 15.6,CaO 0.9, HrO (by ditr.)35.4 percent, corresponding to the formula above.The mineralcan be synthesizedfrom solutions E. P. Mencsen,M. E. Conrns,AND A. E.Ano (1973)Jagowerite: with pH 24 andis readilyobtained by the spontaneousdehydra- A new barium phosphatemineral from the yukon Territory. tion of roesslerite.The Drl curve showsa small endothermic Can. Mineral. 12, 135-136. breakat 95o,a largeone at 135o,and an exothermiipeak at 570.. A gravimetricanalysis (H. Sharples,analyst) gave: BaO 38.41, X-ray studyshows the mineralto be orthorhombic,space group P,O631.41, Al,Os 25.87, Fe,O, 0.26, S 0.15,H,O+ 4.09,total Pbca,a 7.472+0.001,,l0.E9l +0.001, c 16.585+0.005A,Z:8. c 100.19percent. Emission and solid sourcemass spectrographic ca1c.2.326,meas 2.28*0.04 (data on syntheticcrystals, Brasse and analysesindicated the followingelems,rts present in amountsless Pemy,Bull. Soc. Chim. Franc.
    [Show full text]
  • IMA–CNMNC Approved Mineral Symbols
    Mineralogical Magazine (2021), 85, 291–320 doi:10.1180/mgm.2021.43 Article IMA–CNMNC approved mineral symbols Laurence N. Warr* Institute of Geography and Geology, University of Greifswald, 17487 Greifswald, Germany Abstract Several text symbol lists for common rock-forming minerals have been published over the last 40 years, but no internationally agreed standard has yet been established. This contribution presents the first International Mineralogical Association (IMA) Commission on New Minerals, Nomenclature and Classification (CNMNC) approved collection of 5744 mineral name abbreviations by combining four methods of nomenclature based on the Kretz symbol approach. The collection incorporates 991 previously defined abbreviations for mineral groups and species and presents a further 4753 new symbols that cover all currently listed IMA minerals. Adopting IMA– CNMNC approved symbols is considered a necessary step in standardising abbreviations by employing a system compatible with that used for symbolising the chemical elements. Keywords: nomenclature, mineral names, symbols, abbreviations, groups, species, elements, IMA, CNMNC (Received 28 November 2020; accepted 14 May 2021; Accepted Manuscript published online: 18 May 2021; Associate Editor: Anthony R Kampf) Introduction used collection proposed by Whitney and Evans (2010). Despite the availability of recommended abbreviations for the commonly Using text symbols for abbreviating the scientific names of the studied mineral species, to date < 18% of mineral names recog- chemical elements
    [Show full text]
  • New Insight Into the Local Structure of Hydrous Ferric Arsenate Using Full
    New Insight into the Local Structure of Hydrous Ferric Arsenate Using Full-Potential Multiple Scattering Analysis, Density Functional Theory Calculations, and Vibrational Spectroscopy Shaofeng Wang, Xu Ma, Guoqing Zhang, Yongfeng Jia, Keisuke Hatada To cite this version: Shaofeng Wang, Xu Ma, Guoqing Zhang, Yongfeng Jia, Keisuke Hatada. New Insight into the Local Structure of Hydrous Ferric Arsenate Using Full-Potential Multiple Scattering Analysis, Density Func- tional Theory Calculations, and Vibrational Spectroscopy. Environmental Science and Technology, American Chemical Society, 2016, 50 (22), pp.12114-12121. 10.1021/acs.est.6b02703. hal-01437439 HAL Id: hal-01437439 https://hal-univ-rennes1.archives-ouvertes.fr/hal-01437439 Submitted on 12 Jul 2017 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Page 1 of 36 Environmental Science & Technology 1 New insight into the local structure of hydrous ferric arsenate using 2 full-potential multiple scattering analysis, density functional theory calculations, 3 and vibrational spectroscopy 4 5 Shaofeng Wang 1, Xu Ma 1, Guoqing Zhang 1, Yongfeng Jia 2, *, Keisuke Hatada 3 6 7 1. Key Laboratory of Pollution Ecology and Environmental Engineering, Institute of 8 Applied Ecology, Chinese Academy of Sciences, Shenyang, 110016, China 9 2.
    [Show full text]
  • Formulae of Selected Arsenic Minerals Are Listed in Chapter 2, APPENDIX 1 (P
    INDEX Arsenic minerals (in which As is essential to the crystal structure) Formulae of selected arsenic minerals are listed in Chapter 2, APPENDIX 1 (p. 174-183). abernathyite 145 274, 280-282, 295, 297, 301, adamite 23, 31, 39, 44, 115, 116, 118, 240, 304, 317, 350, 355-357, 359, 243, 311, 474, 476, 594, 610-615, 361, 366, 436, 473-475, 477, 620, 624, 627 483, 486, 490-492, 494-497, adelite 23, 111, 112, 476, 477, 519 537, 539, 542, 544, 546, 549, aerugite 130 554, 559, 561-564, 567, 571, agardite 75, 111, 624 574-578, 581, 624 akrochordite 23, 88, 95, 96 arsenovanmeersscheite 145 alarsite 26, 84, 85, 90 arsentsumebite 95, 610-613, 624 algodonite 23 arsenuranospathite 145 alacranite 28, 29 arsenuranylite 145 allactite 23, 24, 104, 124 arthurite 120, 121, 144, 474, 476 alumopharmacosiderite 39, 43, 75, 109 asbecasite 24, 133, 139 andyrobertsite 100, 101, 624 asselbornite 145 angelellite 26, 33, 36, 118, 312, 348, 364 atelestite 128 annabergite 23, 26, 48, 51, 57, 69, attikaite 75, 144 73-76, 96, 274, 476, 627 auriacusite 118 arakiite 143, 144 austinite 23, 112, 244, 474, 476, 594, ardennite 25 612, 613, 620, 624, 627 arhbarite 107 barahonaite-(Al) 75, 144, 146 armangite 23, 131, 138, 141, 142 barahonaite-(Fe) 146 arsenbrackebuschite 95, 624 barian tomichite 140 arsendescloizite 112, 476, 624 bariopharmacosiderite 23, 33, 34, 109 arsenic, native or elemental 3, 4, 218, baumhauerite 23 248, 266, 272, 274, bayldonite 65, 67, 74, 75, 97, 244, 476, 357, 475, 476, 612 594, 602, 603, 610-613, arseniopleite 23, 122 617-619, 621, 624, 627 arseniosiderite
    [Show full text]
  • (Title of the Thesis)*
    ANALYSIS OF CLAY MINERALS IN THE MUDFLATS OF SULFATE-RICH SALINE LAKES by Jennifer Lynn Bentz A thesis submitted to the Department of Geological Sciences and Geological Engineering In conformity with the requirements for the degree of Doctor of Philosophy Queen’s University Kingston, Ontario, Canada (September 28, 2017) Copyright ©Jennifer L. Bentz, 2017 Abstract Clay minerals are important targets for interpreting past environments due to their ubiquity on the surface of terrestrial planets, sensitivity to the prevailing geochemical conditions, and ability to preserve biosignatures. Modern saline lakes that develop sulfate-rich brines are less extensively analyzed due to their relative scarcity compared to those that develop bicarbonate- rich brines. Moreover, most modern sulfate-rich systems are small in area (<100 km2), playa dominated, and rich in detritus making them difficult to sample and to study. Yet, the number and diversity of these lakes makes them important for understanding authigenic mineral formation. The goal of this study was to evaluate authigenic and detrital minerals in the mudflats of sulfate- rich saline lakes. This research focused on microscale (cm) investigations of the mudflats from 23 lakes from the Great Plains of southern Saskatchewan, Canada, and Andean Plateau, Bolivia for a total of 407 sediment samples. For detrital-rich sediments, authigenic illite was consistently found within sand lenses of the mudflats, was rich in Al, Mg, and Fe, and displayed lath-like morphologies. Uncommon minerals were also found containing elements usually in minor/trace quantities that concentrate in the closed-basins. In Laguna Chiar Khota, Bolivia for example, the arsenic-rich minerals realgar and hörnesite were found within the mudflats.
    [Show full text]
  • Profesionăˇlnă Referăˇt
    Journal of the Czech Geological Society, 42/4 (1997) 77 New naturally occurring phases of secondary origin from Jáchymov (Joachimsthal) Nové sekundární minerální fáze z Jáchymova (Czech summary) PETR ONDRUŠ1 - FRANTIŠEK VESELOVSKÝ1 - ROMAN SKÁLA1 - IVANA CÍSAěOVÁ2 - - JAN HLOUŠEK3 - JIěÍ FRÝDA1 - IVAN VAVěÍN1 - JIěÍ ýEJKA4 - ANANDA GABAŠOVÁ1 1 Czech Geological Survey, Klárov 3, 118 21 Prague 1 3 The Faculty of Science, Charles University, Hlavova 2030, 128 43 Prague 2 2 U Roháþových kasáren 24, 100 00 Prague 10 4 National Museum, Václavské námČstí 68, 115 79 Prague 1 This paper describes thirty inorganic compound – secondary mineral phases- found in the nature for the first time. All compounds come from the Jáchymov ore district. All up-to-now available physical and chemical data and references to appropriate literature are given. Crystal structure of phase [ (MoO2)2As2O5(H2O)2] . H2O was solved and refined, crystal structures of Ca(H2AsO4)2 and Mg-villyaellenite were refined by the Rietveld method. Key words: new natural phases, new data, secondary minerals, Jáchymov Introduction Single peak profile fitting procedure using Pearson VII split asymmetric profile shape function implemented In the course of work on the project Study of secon- in the program ZDS ver. 6.01 [291] found angular posi- dary minerals in the Jáchymov ore district (1993 to tions and intensities of reflections in the powder pattern. 1997) [299] we have recognised and studied 30 inor- Diffraction indices were assigned to yielded reflection ganic phases, which were for the first time encountered positions based on theoretical powder pattern calculated as natural materials. This development prompted us to from the crystal structure data with program FullProf write this paper, dedicated exclusively to the new phases.
    [Show full text]
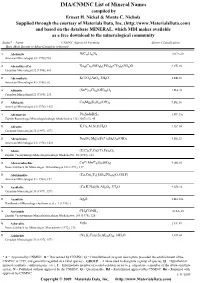
  • IMA/CNMNC List of Mineral Names
    IMA/CNMNC List of Mineral Name s compiled by Ernest H. Nickel & Monte C. Nichols Supplied through the courtesy of Materials Data, Inc. (http://www.MaterialsData.com) and based on the database MINERAL, which MDI makes available as a free download to the mineralogical community Status* Name CNMNC Approved Formula Strunz Classification Best, Most Recent or Most Complete reference. A Abelsonite NiC£¡H£¢N¤ 10.CA.20 American Mineralogist 63 (1978) 930 A Abenakiite-(Ce) Na¢¦Ce¦(SiO£)¦(PO¤)¦(CO£)¦(SO¢)O 9.CK.10 Canadian Mineralogist 32 (1994), 843 G Abernathyite K(UO¢)AsO¤•3H¢O 8.EB.15 American Mineralogist 41 (1956), 82 A Abhurite (SnÀÈ)¢¡Cl¡¦(OH)¡¤O¦ 3.DA.30 Canadian Mineralogist 23 (1985), 233 D Abkhazite Ca¢Mg¥Si¨O¢¢(OH)¢ 9.DE.10 American Mineralogist 63 (1978), 1023 A Abramovite Pb¢SnInBiS§ 2.HF.25a Zapiski Rossiiskogo Mineralogicheskogo Obshchetstva 136 (2007) (5), 45 D Abrazite K,Ca,Al,Si,O,H¢O 9.GC.05 Canadian Mineralogist 35 (1997), 1571 D Abriachanite Na¢(Fe,Mg)£(FeÁÈ)¢Si¨O¢¢(OH)¢ 9.DE.25 American Mineralogist 63 (1978), 1023 D Absite (U,Ca,Y,Ce)(Ti,Fe)¢O¦ Zapiski Vsesoyuznogo Mineralogicheskogo Obshchestva 92 (1963), 113 A Abswurmbachite CuÀÈ(MnÁÈ)¦O¨(SiO¤) 9.AG.05 Neues Jahrbuch für Mineralogie, Abhandlungen 163 (1991), 117 D Abukumalite (Ca,Ce)¢Y£(SiO¤,PO¤)£(O,OH,F) American Mineralogist 51 (1966), 152 D Acadialite (Ca,K,Na)(Si,Al)£O¦•3H¢O 9.GD.10 Canadian Mineralogist 35 (1997), 1571 G Acanthite Ag¢S 2.BA.30a Handbook of Mineralogy (Anthony et al.), 1 (1990), 1 A Acetamide CH£CONH¢ 10.AA.20 Zapiski Vsesoyuznogo Mineralogicheskogo
    [Show full text]