Math 135B: HW #5
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

1 11. Nuclear Chemistry 11.1 Stable and Unstable Nuclides Very Large
11. Nuclear Chemistry Chemical reactions occur as a result of loosing/gaining and sharing electrons in the valance shell which is far away from the atomic nucleus as we described in previous chapters in chemical bonding. In chemical reactions identity of the elements (atomic) and the makeup of the nuclei (mass due to protons and neutrons) is preserved which is reflected in the Law of Conservation of mass. This idea of atomic nucleus is always stable was shattered as Henri Becquerel discovered radioactivity in uranium compound where uranium nuclei changes or undergo nuclear reactions where nuclei of an element is transformed into nuclei of different element(s) while emitting ionization radiation. Marie Curie also began a study of radioactivity in a different form of uranium ore called pitchblende and she discovered the existence of two more highly radioactive new elements radium and polonium formed as the products during the decay of unstable nuclide of uranium-235. Curie measure that the radiation emanated was proportional to the amount (moles or number of nuclides) of radioactive element present, and she proposed that radiation was a property nucleus of an unstable atom. The area of chemistry that focuses on the nuclear changes is called nuclear chemistry. What changes in a nuclide result from the loss of each of the following? a) An alpha particle. b) A gamma ray. c) An electron. d) A neutron. e) A proton. Answer: a), c), d), e) 11.1 Stable and Unstable Nuclides There are stable and unstable radioactive nuclides. Unstable nuclides emit subatomic particles, with alpha −α, beta −β, gamma −γ, proton-p, neutrons-n being the most common. -

Background and Derivation of ANS-5.4 Standard Fission Product Release Model
NUREG/CR-7003 PNNL-18490 Background and Derivation of ANS-5.4 Standard Fission Product Release Model Office of Nuclear Regulatory Research AVAILABILITY OF REFERENCE MATERIALS IN NRC PUBLICATIONS NRC Reference Material Non-NRC Reference Material As of November 1999, you may electronically access Documents available from public and special technical NUREG-series publications and other NRC records at libraries include all open literature items, such as NRC’s Public Electronic Reading Room at books, journal articles, and transactions, Federal http://www.nrc.gov/reading-rm.html. Register notices, Federal and State legislation, and Publicly released records include, to name a few, congressional reports. Such documents as theses, NUREG-series publications; Federal Register notices; dissertations, foreign reports and translations, and applicant, licensee, and vendor documents and non-NRC conference proceedings may be purchased correspondence; NRC correspondence and internal from their sponsoring organization. memoranda; bulletins and information notices; inspection and investigative reports; licensee event reports; and Commission papers and their attachments. Copies of industry codes and standards used in a substantive manner in the NRC regulatory process are NRC publications in the NUREG series, NRC maintained at— regulations, and Title 10, Energy, in the Code of The NRC Technical Library Federal Regulations may also be purchased from one Two White Flint North of these two sources. 11545 Rockville Pike 1. The Superintendent of Documents Rockville, MD 20852–2738 U.S. Government Printing Office Mail Stop SSOP Washington, DC 20402–0001 These standards are available in the library for Internet: bookstore.gpo.gov reference use by the public. Codes and standards are Telephone: 202-512-1800 usually copyrighted and may be purchased from the Fax: 202-512-2250 originating organization or, if they are American 2. -

The Delimiting/Frontier Lines of the Constituents of Matter∗
The delimiting/frontier lines of the constituents of matter∗ Diógenes Galetti1 and Salomon S. Mizrahi2 1Instituto de Física Teórica, Universidade Estadual Paulista (UNESP), São Paulo, SP, Brasily 2Departamento de Física, CCET, Universidade Federal de São Carlos, São Carlos, SP, Brasilz (Dated: October 23, 2019) Abstract Looking at the chart of nuclides displayed at the URL of the International Atomic Energy Agency (IAEA) [1] – that contains all the known nuclides, the natural and those produced artificially in labs – one verifies the existence of two, not quite regular, delimiting lines between which dwell all the nuclides constituting matter. These lines are established by the highly unstable radionuclides located the most far away from those in the central locus, the valley of stability. Here, making use of the “old” semi-empirical mass formula for stable nuclides together with the energy-time uncertainty relation of quantum mechanics, by a simple calculation we show that the obtained frontier lines, for proton and neutron excesses, present an appreciable agreement with the delimiting lines. For the sake of presenting a somewhat comprehensive panorama of the matter in our Universe and their relation with the frontier lines, we narrate, in brief, what is currently known about the astrophysical nucleogenesis processes. Keywords: chart of nuclides, nucleogenesis, nuclide mass formula, valley/line of stability, energy-time un- certainty relation, nuclide delimiting/frontier lines, drip lines arXiv:1909.07223v2 [nucl-th] 22 Oct 2019 ∗ This manuscript is based on an article that was published in Brazilian portuguese language in the journal Revista Brasileira de Ensino de Física, 2018, 41, e20180160. http://dx.doi.org/10.1590/ 1806-9126-rbef-2018-0160. -

Manual for Reactor Produced Radioisotopes
IAEA-TECDOC-1340 Manual for reactor produced radioisotopes January 2003 The originating Section of this publication in the IAEA was: Industrial Applications and Chemistry Section International Atomic Energy Agency Wagramer Strasse 5 P.O. Box 100 A-1400 Vienna, Austria MANUAL FOR REACTOR PRODUCED RADIOISOTOPES IAEA, VIENNA, 2003 IAEA-TECDOC-1340 ISBN 92–0–101103–2 ISSN 1011–4289 © IAEA, 2003 Printed by the IAEA in Austria January 2003 FOREWORD Radioisotopes find extensive applications in several fields including medicine, industry, agriculture and research. Radioisotope production to service different sectors of economic significance constitutes an important ongoing activity of many national nuclear programmes. Radioisotopes, formed by nuclear reactions on targets in a reactor or cyclotron, require further processing in almost all cases to obtain them in a form suitable for use. Specifications for final products and testing procedures for ensuring quality are also an essential part of a radioisotope production programme. The International Atomic Energy Agency (IAEA) has compiled and published such information before for the benefit of laboratories of Member States. The first compilation, entitled Manual of Radioisotope Production, was published in 1966 (Technical Reports Series No. 63). A more elaborate and comprehensive compilation, entitled Radioisotope Production and Quality Control, was published in 1971 (Technical Reports Series No. 128). Both served as useful reference sources for scientists working in radioisotope production worldwide. -

USER's GUIDE: RADIONUCLIDE CARCINOGENICITY Introduction
USER'S GUIDE: RADIONUCLIDE CARCINOGENICITY Introduction EPA classifies all radionuclides as Group A carcinogens. The Radionuclide Table on this website, formerly HEAST Table 4, lists ingestion, inhalation and external exposure cancer slope factors (risk coefficients for total cancer morbidity) for radionuclides in conventional units of picocuries (pCi). (7) Ingestion and inhalation slope factors are central estimates in a linear model of the age-averaged, lifetime attributable radiation cancer incidence (fatal and nonfatal cancer) risk per unit of activity inhaled or ingested, expressed as risk/pCi. External exposure slope factors are central estimates of lifetime attributable radiation cancer incidence risk for each year of exposure to external radiation from photon-emitting radionuclides distributed uniformly in a thick layer of soil and are expressed as risk/yr per pCi/gram soil. When combined with site-specific media concentration data and appropriate exposure assumptions (8), slope factors can be used to estimate lifetime cancer risks to members of the general population due to radionuclide exposures. Intended Users and Applications HEAST users include individuals from the EPA, other Federal agencies, States and contractors who are responsible for the identification, characterization and remediation of sites contaminated with radioactive materials. Radionuclide slope factors are calculated by EPA's Office of Radiation and Indoor Air (ORIA) to assist HEAST users with risk-related evaluations and decision-making at various stages of the remediation process. During site assessment, for example, slope factors are used in EPA's Hazard Ranking System (HRS) to assign toxicity factor values to radionuclides to calculate site scores. During the remedial investigation and feasibility study (RI/FS), slope factors are used to determine baseline site risk, to develop preliminary remediation goals, and to evaluate cleanup alternatives. -

IODINE ISOTOPES & Nuclear Medicine I-123
IODINE ISOTOPES & Nuclear Medicine I-123 ~ I-124 ~ I-125 ~ I-129 ~ I-131 Technical Associates’ Model ~ LiveOne (Radiation Monitor for Live Small Animals) Test data indicate Gamma efficiency on the order of 0.9%, measured with Cs-137, 662 KeV Gammas. I-123 Gammas: 159 KeV (87%) Betas: 127 KeV (13%) Total Maximum Energy: + c.a. 11 (Auger) at 0.05 – 0.5 KeV Half Life: 13.2 hours The detailed decay mechanism is electron capture to form an excited state of the nearly-stable nuclide Tellurium-123 (Its Half Life is so long that it is considered stable for all practical purposes). This excited state of Te-123 produced is not the metastable nuclear isomer Te-123m (the decay of I-123 does not involve enough energy to produce Te-123m). It is a lower-energy nuclear isomer of Te-123 that immediately Gamma decays to ground state Te-123 at the energies noted, or else (13% of the time) decays by internal conversion electron emission (127 keV). This is followed by an average of 11 Auger electrons emitted at very low energies (50-500 eV). The latter decay channel also produces ground-state Te-123. Because of the internal conversion decay channel, I-123 is not an absolutely pure Gamma-emitter, although it is sometimes clinically assumed to be one Iodine-123 Decay Scheme TECHNICAL ASSOCIATES Divisions of OVERHOFF TECHNOLOGY 7051 Eton Ave., Canoga Park, CA 91303 818-883-7043 (Phone) 818-883-6103 (Fax) [email protected] WWW.TECH-ASSOCIATES.COM IODINE ISOTOPES & Nuclear Medicine I-123 ~ I-124 ~ I-125 ~ I-129 ~ I-131 I-124 Gammas: 511 KeV (26%) (from Positron emission) 2.74 MeV, 2.29 MeV, 1.5 MeV, 600 KeV, and others. -

The Physical and Physiological Aspects of Xenon Isotopes in Nuclear Medical Applications
THE PHYSICAL AND PHYSIOLOGICAL ASPECTS OF XENON ISOTOPES IN NUCLEAR MEDICAL APPLICATIONS Magnus Bolmsjö Lund 1981 THE PHYSICAL AND PHYSIOLOGICAL ASPECTS OF XENON ISOTOPES IN NUCLEAR MEDICAL APPLICATIONS av MAGNUS BOLMSJD Fil.kand., Kim Akademisk avhandling som fur avläggande av filosofie doktorsexamen vid matematifik-miturvetenskapliKa fakul- teten vid Universitetet i Lund kommer att offentligen försvaras I Fysiska Institutionen, sal B, Sölvegatan 14, Lund, fredagen den 27 november 1981 kl 10.15. LUNDF6/(NFRA-1014)/1-46/(1981) LUMEDW/(MERI-1014)/1-46/(1981) THE PHYSICAL AND PHYSIOLOGICAL ASPECTS OF XENON ISOTOPES IN NUCLEAR MEDICAL APPLICATIONS Magnus Bolmsjö Lund 1981 OrgMuxaboa Document name LUND UNIVERSITY DOCTORAL DISSERTATION Radiation Physics Department Date of issue 1981-11-27 Lasarettet CODEN LUNDF6/(NFRA-1(>'4)/1-46/(1981) S-221 85 LUND, Sv* iden LUMEDW/(MERI-1014)/1-46/(1981) Authors) Sponsoring organization Magnus Bolmsjö Title and subtitle THE PHYSICAL AND PHYSIOLOGICAL ASPECTS OF XENON ISOTOPES IN NUCLEAR MEDICAL APPLICATIONS. Abstract A method for trapping radioactive xenon waste from nuclear medical departments has been investigated. Adsorption of xenon on activated charcoal was found to be an effi- cient trapping method. A large gain in capacity was found when the trap was refrigera- ted, and permitted a large number of patient investigations before break-through of xenon occurred. By heating charcoal traps to 250-350°C, adsorbed xenon gas is freed and is thus made available for re-use. A technique for room-air monitoring of xenon-leakage from patient investigations is described, where the room-air is continously pumped through a small charcoal filter, mounted close to a detector. -

Chapter 11 the Nucleus
Chapter 11 The Nucleus Introduction Most of the physical and chemical properties of matter which we are familiar with are a result of the number and configuration of atomic electrons. That's why we have spent most of the course to date concentrating topics related to atomic electrons. Nevertheless, atomic nuclei are vitally important for a number of reasons, including: ·The number of electrons an atom can have depends on how many protons the nuclei has. Thus, the nucleus plays a large, if indirect, role in determining atomic structure. ·Most of the energies liberated in everyday processes involve nuclear reactions. The first couple of sections of this chapter describe several problems the nucleus presents us with. For example, consider this problem. Take two protons at their approximate separation in the nucleus. Calculate the repulsive Coulomb energy between them. e2 V = = (1.6x10-19 )2 (9x109)(1015)(1/ (1.6x10-19)) » 1.4x106 eV = 1.4MeV. 4p e0 r That's a large repulsive potential. Now imagine the repulsive Coulomb energy for several dozen protons packed tightly into a nucleus. We have a major problem here. How can a nucleus stick together? A logical guess is that the nucleus contains electrons, which reduce the Coulomb repulsion. 11.1 Nuclear Composition It is quite logical to assume that nuclei contain electrons. For example, a good guess might be that half of an atom's electrons are contained within the nucleus, and reduce the electrostatic repulsive forces between protons. Besides the Coulomb repulsion mentioned above, facts which suggest the nucleus might contain electrons are nuclide masses, which are nearly multiples of the hydrogen mass (which contains an electron). -

Chapter 18 Nuclear Chemistry
CHAPTER 18 NUCLEAR CHEMISTRY tan is going to visit his son Fred at the radiology department of a local research 18.1 The Nucleus and hospital, where Fred has been recording the brain activity of kids with learning Radioactivity differences and comparing it to the brain activity of kids who excel in normal 18.2 Uses of school environments. To pursue this research, Fred uses imaging technology Radioactive developed through the science of nuclear chemistry, the study of changes that occur Substances within the nuclei of atoms. But even before getting into his car to go see Fred, Stan 18.3 Nuclear Energy is already surrounded by substances undergoing nuclear reactions. In fact, nuclear reactions accompany Stan wherever he goes. He has strontium-90 in his bones and iodine-131 in his thyroid, and both substances are constantly undergoing nuclear reactions of a type known as beta emission. Stan is not unique in this respect. All of our bodies contain these substances and others like them. Stan is surrounded by nuclear changes that take place outside his body, as well. The soil under his house contains a small amount of uranium-238, which undergoes a type of nuclear reaction called alpha emission. A series of changes in the nucleus of the uranium-238 leads to an even smaller amount of radon-222, which is a gas that he inhales in every breath he takes at home. Subsequently, radon-222 undergoes a nuclear reaction very similar to the reaction for uranium-238. On Stan’s way to the hospital, he passes a nuclear power plant that generates electricity for the homes and businesses in his city by means of yet another kind of nuclear reaction. -

Atomic and Nuclear Physics
Atomic and Nuclear Physics Course No: N05-001 Credit: 5 PDH Gilbert Gedeon, P.E. Continuing Education and Development, Inc. 22 Stonewall Court Woodcliff Lake, NJ 07677 P: (877) 322-5800 [email protected] Department of Energy Fundamentals Handbook NUCLEAR PHYSICS AND REACTOR THEORY Module 1 Atomic and Nuclear Physics Atomic and Nuclear Physics DOE-HDBK-1019/1-93 TABLE OF CONTENTS TABLE OF CONTENTS LIST OF FIGURES.................................................. iv LIST OF TABLES .................................................. v REFERENCES ..................................................... vi OBJECTIVES...................................................... vii ATOMIC NATURE OF MATTER ....................................... 1 Structure of Matter ............................................. 1 Subatomic Particles............................................. 2 Bohr Model of the Atom......................................... 3 Measuring Units on the Atomic Scale................................ 4 Nuclides..................................................... 4 Isotopes..................................................... 6 Atomic and Nuclear Radii ........................................ 6 Nuclear Forces................................................ 7 Summary.................................................... 9 CHART OF THE NUCLIDES ......................................... 11 Chart of the Nuclides........................................... 11 Information for Stable Nuclides ................................... 13 Information for -
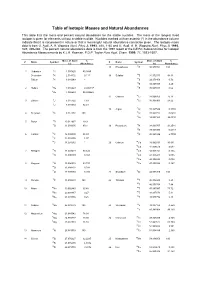
Table of Isotopic Masses and Natural Abundances
Table of Isotopic Masses and Natural Abundances This table lists the mass and percent natural abundance for the stable nuclides. The mass of the longest lived isotope is given for elements without a stable nuclide. Nuclides marked with an asterisk (*) in the abundance column indicate that it is not present in nature or that a meaningful natural abundance cannot be given. The isotopic mass data is from G. Audi, A. H. Wapstra Nucl. Phys A. 1993, 565, 1-65 and G. Audi, A. H. Wapstra Nucl. Phys A. 1995, 595, 409-480. The percent natural abundance data is from the 1997 report of the IUPAC Subcommittee for Isotopic Abundance Measurements by K.J.R. Rosman, P.D.P. Taylor Pure Appl. Chem. 1999, 71, 1593-1607. Mass of Atom % Mass of Atom % Z Name Symbol Z Name Symbol (u) Abundance (u) Abundance 15 Phosphorus 31P 30.973762 100 1 Hydrogen 1H 1.007825 99.9885 Deuterium 2H 2.014102 0.115 16 Sulphur 32S 31.972071 94.93 Tritium 3H 3.016049 * 33S 32.971458 0.76 34S 33.967867 4.29 2 Helium 3He 3.016029 0.000137 36S 35.967081 0.02 4He 4.002603 99.999863 17 Chlorine 35Cl 34.968853 75.78 3 Lithium 6Li 6.015122 7.59 37Cl 36.965903 24.22 7Li 7.016004 92.41 18 Argon 36Ar 35.967546 0.3365 4 Beryllium 9Be 9.012182 100 38Ar 37.962732 0.0632 40Ar 39.962383 99.6003 5 Boron 10B 10.012937 19.9 11B 11.009305 80.1 19 Potassium 39K 38.963707 93.2581 40K 39.963999 0.0117 6 Carbon 12C 12.000000 98.93 41K 40.961826 6.7302 13C 13.003355 1.07 14C 14.003242 * 20 Calcium 40Ca 39.962591 96.941 42Ca 41.958618 0.647 7 Nitrogen 14N 14.003074 99.632 43Ca 42.958767 0.135 15N 15.000109 -

Chapter 21 Nuclear Chemistry
Chemistry, The Central Science , 10th edition Theodore L. Brown; H. Eugene LeMay, Jr.; and Bruce E. Bursten PDF Created with deskPDF PDFWriter -Trial::http://www.docudesk.com Chapter 21 Nuclear Chemistry John D. Bookstaver St. Charles Community College St. Peters, MO Nuclear 2006, Prentice Hall, Inc. Chemistry PDF Created with deskPDF PDFWriter -Trial::http://www.docudesk.com The Nucleus • Remember that the nucleus is comprised of the two nucleons , protons and neutrons. • The number of protons is the atomic number. • The number of protons and neutrons together is effectively the mass of the atom. Nuclear Chemistry PDF Created with deskPDF PDFWriter -Trial::http://www.docudesk.com Isotopes • Not all atoms of the same element have the same mass due to different numbers of neutrons in those atoms. • There are three naturally occurring isotopes of uranium: Uranium-234 Uranium-235 Uranium-238 Nuclear Chemistry PDF Created with deskPDF PDFWriter -Trial::http://www.docudesk.com Radioactivity • It is not uncommon for some nuclides of an element to be unstable, or radioactive . • We refer to these as radionuclides . • There are several ways radionuclides can decay into a different nuclide. Nuclear Chemistry PDF Created with deskPDF PDFWriter -Trial::http://www.docudesk.com Nuclear Equations 238 → 234 4 92 U 90 Th + 2He • In a nuclear reaction the atomic mass and atomic number has to add up in the reactants and the products. Nuclear Chemistry What product is formed when radium-226 undergoes PDF Created with deskPDF PDFWriter -Trial::http://www.docudesk.com