Open Chong Ai-Dissertation.Pdf
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
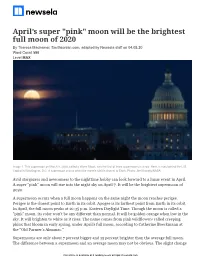
April's Super "Pink" Moon Will Be the Brightest Full Moon of 2020
April’s super "pink" moon will be the brightest full moon of 2020 By Theresa Machemer, Smithsonian.com, adapted by Newsela staff on 04.05.20 Word Count 590 Level MAX Image 1. This supermoon on March 9, 2020, called a Worm Moon, was the first of three supermoons in a row. Here, it rises behind the U.S. Capitol in Washington, D.C. A supermoon occurs when the moon's orbit is closest to Earth. Photo: Joel Kowsky/NASA Avid stargazers and newcomers to the nighttime hobby can look forward to a lunar event in April. A super "pink" moon will rise into the night sky on April 7. It will be the brightest supermoon of 2020. A supermoon occurs when a full moon happens on the same night the moon reaches perigee. Perigee is the closest point to Earth in its orbit. Apogee is its farthest point from Earth in its orbit. In April, the full moon peaks at 10:35 p.m. Eastern Daylight Time. Though the moon is called a "pink" moon, its color won't be any different than normal. It will be golden orange when low in the sky. It will brighten to white as it rises. The name comes from pink wildflowers called creeping phlox that bloom in early spring, under April's full moon, according to Catherine Boeckmann at the "Old Farmer's Almanac." Supermoons are only about 7 percent bigger and 15 percent brighter than the average full moon. The difference between a supermoon and an average moon may not be obvious. -

Glossary Glossary
Glossary Glossary Albedo A measure of an object’s reflectivity. A pure white reflecting surface has an albedo of 1.0 (100%). A pitch-black, nonreflecting surface has an albedo of 0.0. The Moon is a fairly dark object with a combined albedo of 0.07 (reflecting 7% of the sunlight that falls upon it). The albedo range of the lunar maria is between 0.05 and 0.08. The brighter highlands have an albedo range from 0.09 to 0.15. Anorthosite Rocks rich in the mineral feldspar, making up much of the Moon’s bright highland regions. Aperture The diameter of a telescope’s objective lens or primary mirror. Apogee The point in the Moon’s orbit where it is furthest from the Earth. At apogee, the Moon can reach a maximum distance of 406,700 km from the Earth. Apollo The manned lunar program of the United States. Between July 1969 and December 1972, six Apollo missions landed on the Moon, allowing a total of 12 astronauts to explore its surface. Asteroid A minor planet. A large solid body of rock in orbit around the Sun. Banded crater A crater that displays dusky linear tracts on its inner walls and/or floor. 250 Basalt A dark, fine-grained volcanic rock, low in silicon, with a low viscosity. Basaltic material fills many of the Moon’s major basins, especially on the near side. Glossary Basin A very large circular impact structure (usually comprising multiple concentric rings) that usually displays some degree of flooding with lava. The largest and most conspicuous lava- flooded basins on the Moon are found on the near side, and most are filled to their outer edges with mare basalts. -

Syzygies a Conjunction Or an Opposition of the Sun with the Moon Occurs When the Elongation Between the Two Luminaries Is 0° Or
CHAPTER THIRTEEN SYZYGIES A conjunction or an opposition of the Sun with the Moon occurs when the elongation between the two luminaries is 0° or 180°, respec- tively. Syzygy is an astronomical term that refers both to conjunction and opposition. At mean syzygy, the double elongation, 2η ̄ = 0°, where ̄ ̄ ̄ ̄ η ̄ = λm – λs, and λm and λs are the mean longitudes of the Moon and the Sun. Analogously, at true syzygy, the double elongation, 2η = 0°, where η = λm – λs, and λm and λs are the true longitudes of the Moon and the Sun. The determination of the time from mean to true syzygy, ∆t, an essential step in the calculation of eclipses, was historically one of the major problems considered in computational astronomy (Chabás and Goldstein 1992 and 1997). Figure 20 represents a mean conjunction of the Sun and the Moon (indicated by the direction of S ̄ and M̄ ) and its corresponding true conjunction (indicated by the direction of S´ and M´). In this case, the ̄ ̄ mean conjunction (when λs = λm), which takes place at time t, comes M S̅ M̅ S S’ M’ λ’ = λ’s O m Aries 0° ̅̅ λλm = s Figure 20: Mean and true syzygies 140 chapter thirteen Table 13.1A: Some historical values of the mean synodic month Mean synodic month 29;31,50,7,37,27,8,25d Parisian Alfonsine Tables 29;31,50,7,54,25,3,32d Levi ben Gerson 29;31,50,8,9,20d al-Ḥajjāj’s Arabic trans. of the Almagest, Copernicus 29;31,50,8,9,24d Ibn Yūnus, al-Bitrūjị̄ 29;31,50,8,14,38d Ibn al-Kammād 29;31,50,8,19,50d al-Battānī 29;31,50,8,20d Almagest, Toledan Tables after the true conjunction λ( s´ = λm´), which occurs at time t´, so that ∆t = t´ – t < 0. -
![Who We Are… Syz-Y-Gy [Siz-Ehh-Jee] – N. a Perfect Astronomical Alignment of Three Objects Such As the Sun the Earth And](https://docslib.b-cdn.net/cover/8683/who-we-are-syz-y-gy-siz-ehh-jee-n-a-perfect-astronomical-alignment-of-three-objects-such-as-the-sun-the-earth-and-728683.webp)
Who We Are… Syz-Y-Gy [Siz-Ehh-Jee] – N. a Perfect Astronomical Alignment of Three Objects Such As the Sun the Earth And
Who we are… Solving the toughest information awareness challenges for those in harm’s way Syzygy prides ourselves on leaning forward to support those that protect the homeland. From supporting hurricane response to providing technology to secure our borders Syzygy always delivers. TAK Development Capabilities General Capabilities • Syzygy develops code across all TAK • Software development: Linux, Windows, iOS, platforms: ATAK, plugins, iTAK, TAK Server, Android, DevOps/Cloud WinTAK, WebTAK • AWS, GovCloud, Azure, and FirstNet • Full DevOps team for auto-deployment for Developers on-prem TAK Infrastructure solutions • Custom geospatial applications • TAK Integration / Plugin development for • Integration expertise: sUAS, CUAS, EO/IR, communications (MANET/SATCOM), sensors radar, communications (camera/radar/sUAS/CUAS) • Mobile Ad-Hoc Network (MANET) subject • Full training capabilities – End User, Admin, matter experts: design, deployment, Train the Trainer integration, sustainment • Full sustainment capabilities – • Security experts: DISA STIG software/infrastructure maintenance, implementation/automation helpdesk • Cloud automation • Field support for operational training/deployment • Training Development & Delivery • General TAK operational subject matter • Hardware Development expertise • Full system development, deployment, and sustainment syz-y-gy [siz-ehh-jee] – n. A perfect astronomical alignment of three objects such as the sun the earth and the moon For More Information Contact: [email protected] | www.syzygyintegration.com Equipment described herein is subject to US export regulations and may require a license prior to export. Diversion contrary to US law is prohibited. Imagery for illustration purposes only. Specifications are subject to change without notice. SNAP is a registered trademark of Syzygy Integration LLC. ©2020 Syzygy Integration LLC Simple Network Access Point Enterprise services ... at the operational edge SNAP-E (Edge) pushes enterprise services to the operational edge. -

Orbital Resonance and Solar Cycles by P.A.Semi
Orbital resonance and Solar cycles by P.A.Semi Abstract We show resonance cycles between most planets in Solar System, of differing quality. The most precise resonance - between Earth and Venus, which not only stabilizes orbits of both planets, locks planet Venus rotation in tidal locking, but also affects the Sun: This resonance group (E+V) also influences Sunspot cycles - the position of syzygy between Earth and Venus, when the barycenter of the resonance group most closely approaches the Sun and stops for some time, relative to Jupiter planet, well matches the Sunspot cycle of 11 years, not only for the last 400 years of measured Sunspot cycles, but also in 1000 years of historical record of "severe winters". We show, how cycles in angular momentum of Earth and Venus planets match with the Sunspot cycle and how the main cycle in angular momentum of the whole Solar system (854-year cycle of Jupiter/Saturn) matches with climatologic data, assumed to show connection with Solar output power and insolation. We show the possible connections between E+V events and Solar global p-Mode frequency changes. We futher show angular momentum tables and charts for individual planets, as encoded in DE405 and DE406 ephemerides. We show, that inner planets orbit on heliocentric trajectories whereas outer planets orbit on barycentric trajectories. We further TRY to show, how planet positions influence individual Sunspot groups, in SOHO and GONG data... [This work is pending...] Orbital resonance Earth and Venus The most precise orbital resonance is between Earth and Venus planets. These planets meet 5 times during 8 Earth years and during 13 Venus years. -

A Novel Elysium by Evan Crichton Anderson a PROJECT Submitted To
A Novel Elysium by Evan Crichton Anderson A PROJECT submitted to Oregon State University University Honors College in partial fulfillment of the requirements for the degree of Honors Baccalaureate of Arts in English (Honors Associate) Presented May 27, 2014 Commencement June 2014 1 AN ABSTRACT OF THE THESIS OF Evan Crichton Anderson for the degree of Honors Baccalaureate of Arts in English presented on May 27, 2014 . Title: A Novel Elysium . Abstract approved: ______________________________________________ Steven Kunert As a metafictional work of science fiction literature, A Novel Elysium explores the timelessness of both the human mind and its literary surroundings, comparing the self-awareness of its characters to the sometimes tragic or empowering metaphysical realizations of human beings. Within this framework, any concrete place or time is unimportant; temporal and physical locations are created by the relations of the characters to their world and also by the relations of the readers to this text. The subjects are art, intention, pleasure, perception, and existence, and each character comes to know these or become undone by them at the conclusion of A Novel Elysium , just as the reader comes to realize they are being directly addressed, rather than shown an unrelated fictional tale. Drawing on the full imaginative and mnemonic powers of its characters, the work abounds with references both to other literary classics and to itself, creating a semi-circular dialectic about the perceived relationships between past, present, future, -

Astronomy Magazine Article
he wild year of 2020 otherwise. And although I don’t keep in con- boasted two solar eclipses: stant contact with every one of them, when an annular eclipse on June an eclipse passes overhead anywhere in the 21 and a total solar eclipse world, I have a good chance of hearing from on December 14. Travel some of my old friends who are eager to restrictions prevented share their new pictures. North Americans, as well At the time of this writing, the next solar Tas many others in the Western Hemisphere, eclipse to be seen from Earth will be total, from viewing the path of annularity that with its peak occurring near the Argentina/ stretched from Africa through the Middle Chile border on December 14, 2020. Be sure East to Pakistan, India, mainland China, and to keep an eye out for images of December’s Taiwan. Fortunately, local eclipse viewers total solar eclipse in future issues of who managed to get beneath the Moon’s Astronomy. Corona shadow captured wonderful images of the Meanwhile, the next annular eclipse will breathtaking event. be on June 10, 2021. Its path will trek from The following is a smattering of shots southern Canada over the North Pole and from last June’s annular eclipse, which I down to the Russian Far East. Observers in monitored into the wee hours of the morn- the northeastern United States will be happy ing with the help of email, the web, and to learn that partial phases of this annular livestreams from the Middle East and Asia. -

The Solar System (PDF)
Colgrove. W.G. A Ready Reference Handbook of the SOLAR SYSTEM ROYAL ASTRONOMICAL SOCIETY OF CANADA • LONDON CENTRE DEPARTMENT OF ASTRONOMY UNIVERSITY OF WESTERN ONTARIO LONDON, ONTARIO PLEASE KEEP CARDS IN THIS POCKET RESOURCE CENTRE ROYAL ASTRONOMICAL SOCIETY OF CANADA - LONDON CENTRE DEPARTMENT OF ASTRONOMY, UNIVERSITY OF WESTERN ONTARIO. LONDON, ONTARIO THE MODEL PLANETARIUM See Appendix — A — Ready Reference Handbook of the SOLAR SYSTEM A CONCISE SUMMARY OF OVER 1,000 Interesting Items and Deductions By W. G. COLGROVE, M.A., B.D. 2 Christie St., London, Ont. COPYRIGHT, CANADA, 1933 BY W. G. COLGROVE, M.A., B.D. Dedication This handbook is dedicated to the amateur astronomers who have done so much to make their inspiring hobby popular. PREFACE This little volume is the result of several years of careful search in many libraries in Canada and the United States for the most informing and reliable data about the various members of the Solar System. Our object is to furnish the reader with a simple summary of fact and theory so that he may obtain an adequate understanding of this very interesting part of astron omical study. Most of the material in these pages was published in the Journal of the Royal Astronomical Society of Canada in recent years. Some necessary brief chapters have been added and for the sake of uniformity in treatment as well as for easy reference and comparison the same number and order of items has been given for each member of the System, although some do not apply in the case of the sun and the earth. -

Climate Change Issue
FALL 2020 The founders, investors, corporations, and policies helping solve CLIWe climate change. MATE can CHAN fix GEit. 06 A home for Tough Tech founders. The Engine, built by MIT, is a venture frm that invests in early-stage companies solving the world’s biggest problems through the convergence of breakthrough science, engineering, and leadership. Our mission is to accelerate the path to market for Tough Tech companies by providing access to a unique combination of investment, infrastructure, and a vibrant ecosystem. Tough Tech Publication 06 October,2020 The Engine, Built by MIT Edited & Produced by: Nathaniel Brewster Design: www.draft.cl Print by: Puritan Capital, NH & MA CONTENTS 04 Introduction 06 Cleantech’s Comeback 12 Thoughts on a Changing Climate 28 A Survey of Companies and Technologies 56 The Engine Portfolio Companies 76 The Engine Network 77 Tough Tech’s New Home INTRODUCTION A Climate of Hope In an era of great uncertainty, I remain optimistic. For every group of founders in which we invest, dozens of others are also pursuing solutions to challenges like climate change. | TOUGH TECH 06 4 Last month, as multiple hurricanes those at the forefront of the cleantech existential imperative of deploying barreled toward the Gulf Coast and revolution, recording their perspectives capital in cleantech startups as well wildfre spread unchecked through on the present and future of sustain- as the necessity of an infrastructure the West, the threat of climate change able technologies, climate policy, and to support technology and business became tangible for many Americans. investment. I suspect you will fnd their development as effciently as possible. -

Our Place in the Solar System
dit: k Fie nbe / rg Tra vel Qu est Inte rnat ion al / Wil nes Tra 2Cre Ric der s vel Our Place in the Solar System Sun, Earth, Moon & Eclipses Activity Guide Image Credit: images.nasa.gov CREDITS FOR ACTIVITIES AND RESOURCES This Activity Guide was developed by the Girl Scout Stars team at the SETI Institute, ARIES Scientific, Inc., Girl Scouts of Northern California, Girl Scouts of the USA, University of Arizona , and the Astronomical Society of the Pacific. Louis Mayo and Edna DeVore co-authored this booklet of activities, with significant contributions by Pamela Harman, Larry Lebofsky, Vivian White, Theresa Summer, Jean Fahy, Jessica Henricks, Elspeth Kersh, and Wendy Chin. Further contributions were made by Joanne Berg, Cole Grissom, Amanda Hudson, Don McCarthy, and Wendy Friedman. The team was led by Edna DeVore, Principal Investigator of “Reaching for the Stars: NASA Science for Girl Scouts,” which is funded by NASA Cooperative Agreement #NNX16AB90A. Updated Jan 2020 P. Harman / D. Richardson. ACTIVITY OR RESOURCE AUTHOR and SOURCES LIVING IN A BUBBLE—PLAY WITH MAGNETS AND COMPASSES L. Mayo, and Multiverse—UC Berkeley Space Sciences Lab SUNBURN—ULTRAVIOLET LIGHT DETECTORS L. Mayo, E. DeVore SEEING THE INVISIBLE—INFRARED LIGHT DETECTORS L. Mayo, NASA Airborne Astronomy Ambassadors LET’S SEE LIGHT IN A NEW WAY—DIFFRACTION SPECTRA L. Mayo, E. DeVore A LIGHT SNACK—COOKIE BOX SPECTROMETERS L. Mayo, E. DeVore, NASA: The Science of the sun MAKE SUN S’MORES! NASA Climate Kids HOW BIG IS BIG? SOLAR PIZZAS L. Mayo, NASA sun-Earth Day EARTH AS A PEPPERCORN—SIZE AND SCALE OF THE SOLAR SYSTEM Guy Ottwell, The Thousand Yard Model SUN TRACKING J. -

Supermoon - What It Is and When It Occurs
SuperMoon - What It Is and When It Occurs The Moon travels around Earth in an elliptical orbit. Because the orbit is egg-shaped (and not circular, where the distance between the two would always be the same), once a month the Moon is at perigee (closest to the Earth) and once a month it's at apogee (farthest from the Earth). Sometimes the Sun, Moon and Earth are all in alignment. When Earth is in the middle of the three, we have a "full Moon." When the Moon is in the middle, we have a "new Moon." Scientists refer to the alignment of these three bodies as a "syzygy." Every now and again, during such an alignment, the Moon is full when it's at perigee (closest to Earth). Scientists call that event a "perigee-syzygy," but most everyone else calls it a "SuperMoon." The next one is due on April 7-8, 2020 (which will be the biggest full moon of 2020). At that time, the Moon will be closest to Earth (221,851 miles/357,035 kilometers away) compared to its average distance of 238,855 miles/384,400 km). A stunningly beautiful Super-Moon event occurred on the 19th of March, 2011—the largest and brightest in nearly twenty years. The video clip at the top of this page, narrated by NASA's Dr. Tony Phillips, explains this awesome "perigee moon" in greater detail. In light of 2011 earthquakes in New Zealand and Japan, many people wondered whether the SuperMoon (and/or increased solar-flare activity) that year had any causal relationship to those events. -

A History and Test of Planetary Weather Forecasting
University of Massachusetts Amherst ScholarWorks@UMass Amherst Open Access Dissertations 5-2010 A History and Test of Planetary Weather Forecasting Bruce Scofield University of Massachusetts Amherst Follow this and additional works at: https://scholarworks.umass.edu/open_access_dissertations Part of the Geology Commons Recommended Citation Scofield, Bruce, A" History and Test of Planetary Weather Forecasting" (2010). Open Access Dissertations. 221. https://scholarworks.umass.edu/open_access_dissertations/221 This Open Access Dissertation is brought to you for free and open access by ScholarWorks@UMass Amherst. It has been accepted for inclusion in Open Access Dissertations by an authorized administrator of ScholarWorks@UMass Amherst. For more information, please contact [email protected]. A HISTORY AND TEST OF PLANETARY WEATHER FORECASTING A Dissertation Presented by BRUCE SCOFIELD Submitted to the Graduate School of the University of Massachusetts Amherst in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY May 2010 Geosciences © Copyright by Bruce Scofield 2010 All Rights Reserved A HISTORY AND TEST OF PLANETARY WEATHER FORECASTING A Dissertation Presented by BRUCE SCOFIELD Approved as to style and content by: ______________________________________ Lynn Margulis, Chair _______________________________________ Robert M. DeConto, Member _______________________________________ Frank Keimig, Member _______________________________________ Brian W. Ogilvie, Member _______________________________________ Theodore D. Sargent, Member _______________________________________ R. Mark Leckie, Department Head Department of Geosciences ACKNOWLEDGEMENTS I would like to first thank my advisor, Lynn Margulis, for her recognition that my unconventional thesis lies within the boundaries of the geosciences. She understands very well how ideas in science come in and out of fashion and things that were dismissed or ignored in the past may very well be keys to future insights.