Learning Physics with Mathematical Modelling
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Edição De Natal !
Ano II - Número 5 A revista eletrônica do entusiasta de videogames e microcomputadores clássicos Visitamos a Cinótica! EDIÇÃO DE NATAL ! Entrevistas Internacionais: Ralph Baer Howard S. Warshaw Reviews Especiais: . Prince of Persia . Em Busca dos Tesouros JOGOS 80 1 INDICE C.P.U. EXPEDIENTE Beta - O Retorno ...................................... 04 Jogos 80 é uma publicação da Dickens Editora Virtual. Editor CURIOSIDADES Marcus Vinicius Garrett Chiado Konami´s Synthesizer .............................. 24 Visita à Cinótica ...................................... 22 Co-Editor Eduardo Antônio Raga Luccas Redatores desta Edição EDITORIAL .......................................... 03 Carlos Bragatto Eduardo Antônio Raga Luccas Ericson Benjamin Jorge Braga da Silva JOYSTICK Marcelo Tini E.T. Phone Home! .................................... 17 Marcus Vinicius Garrett Chiado Em Busca dos Tesouros ........................... 09 Murilo Saraiva de Queiroz Fiendish Freddy’s Big Top O’ Fun ............ 15 Revisão M.A.S.H. .................................................. 14 Eduardo Antônio Raga Luccas Prince of Persia ........................................ 11 Marcus Vinicius Garrett Chiado Logotipo Rick Zavala PERSONALIDADES Howard Scott Warshaw .......................... 19 Projeto gráfico e diagramação Ralph Baer .............................................. 06 LuccasCorp. Computer Division Agradecimentos André Saracene Forte TELEX Carlos Bragatto Fernando Salvio Especial: Depoimentos de Natal ............ 25 Howard Scott Warshaw Ralph Baer -

Tecnologias Da Informação E Comunicação
Referências: Guia da Exposição "Memórias das Tecnologias e dos Sistemas de Informação" www.memtsi.dsi.uminho.pt Colecção: memTSI, DSI e Alfamicro http://piano.dsi.uminho.pt/museuv Departamento de Sistemas de Informação da UM www.memtsi.dsi.uminho.pt http://piano.dsi.uminho.pt/museuv || Sinclair ZX81 || Sinclair ZX SPECTRUM || TIMEX 1500 || TIMEX TC 2068 Máquina lançada em 1981, Lançado em 1982, foi um O Timex 1500 foi criado em O Timex TC 2068 foi TECNOLOGIAS com 1K de memória (max dos maiores sucessos Julho de 1983 e era desenvolvido no final de 16K), sem som e sem cor. comerciais no mercado dos basicamente um sinclair 1983 com um processador “home computers”, Z81 com 16KB de RAM Z80A a 3,5 Mhz. DA INFORMAÇÃO desenhado e comercializado incorporada com Dispunha de 48KB de por uma empresa do Reino possibilidade de expansão memória RAM e 16KB de E COMUNICAÇÃO Unido (Sinclair) por poucas até 64KB. memória ROM. TIC dezenas de contos (o preço Tinha um processador Dispunha de conectores de lançamento foi £129.95 ZILOG Z80A que funcionava para monitor, joystick, no Reino Unido). a uma velocidade de 3,5Mhz. leitor/gravador de casetes, Descendente directo do A imagem em ecrã era a 2 porta de expansão e ZX81, incorporou cor e som. cores com uma resolução televisão, usando um sinal Configuração completa com de 64x44. PAL. impressora térmica Sinclair Em modo de texto permitia Tinha uma resolução de 2040 e um gravador áudio 32 colunas e 24 linhas. 256x192 píxeis e permitia (periférico de arquivo) e Não dispunha de som. -
Melbourne House at Our Office Books and Software That Melbourne House Has Nearest to You: Published for a Wide Range of Microcomputers
mELBDLIAnE HO LISE PAESEnTS camPLITEA BDDHSB SDFTWAAE Me·lbourne House is an international software publishing company. If you have any difficulties obtaining some Dear Computer User: of our products, please contact I am very pleased to be able to let you know of the Melbourne House at our office books and software that Melbourne House has nearest to you: published for a wide range of microcomputers. United States of America Our aim is to present the best possible books and Melbourne House Software Inc., software for most home computers. Our books 347 Reedwood Drive, present information that is suitable for the beginner Nashville TN 37217 computer user right through to the experienced United Kingdom computer programmer or hobbyist. Melbourne House (Publishers) Ltd., Our software aims to bring out the most possible Glebe Cottage, Glebe House, from each computer. Each program has been written to be a state-of-the-art work. The result has been Station Road, Cheddington, software that has been internationally acclaimed. Leighton Buzzard, Bedfordshire, LU77NA. I would like to hear from you if you have any comments or suggestions about our books and Australia & New Zealand software, or what you would like to see us publish. Melbourne House (Australia) Pty. Ltd., Suite 4, 75 Palmerston Crescent, If you have written something for your computer-a program, an article, or a book-then please send it to South Melbourne, Victoria 3205. us. We will give you a prompt reply as to whether it is a work that we could publish. I trust that you will enjoy our books and software. -

Aboard the Impulse Train: an Analysis of the Two- Channel Title Music Routine in Manic Miner Kenneth B
All aboard the impulse train: an analysis of the two- channel title music routine in Manic Miner Kenneth B. McAlpine This is the author's accepted manuscript. The final publication is available at Springer via http://dx.doi.org/10.1007/s40869-015-0012-x All Aboard the Impulse Train: An analysis of the two-channel title music routine in Manic Miner Dr Kenneth B. McAlpine University of Abertay Dundee Abstract The ZX Spectrum launched in the UK in April 1982, and almost single- handedly kick-started the British computer games industry. Launched to compete with technologically-superior rivals from Acorn and Commodore, the Spectrum had price and popularity on its side and became a runaway success. One area, however, where the Spectrum betrayed its price-point was its sound hardware, providing just a single channel of 1-bit sound playback, and the first-generation of Spectrum titles did little to challenge the machine’s hardware. Programmers soon realised, however, that with clever machine coding, the Spectrum’s speaker could be encouraged to do more than it was ever designed to. This creativity, borne from constraint, represents a very real example of technology, or rather limited technology, as a driver for creativity, and, since the solutions were not without cost, they imparted a characteristic sound that, in turn, came to define the aesthetic of ZX Spectrum music. At the time, there was little interest in the formal study of either the technologies that support computer games or the social and cultural phenomena that surround them. This retrospective study aims to address that by deconstructing and analysing a key turning point in the musical life of the ZX Spectrum. -

ED 278 545 AUTHOR Conference on Science and Technology
DOCUMENT RESUME ED 278 545 SE 047 709 AUTHOR Thulstrup, Erik W., Ed. TITLE Proceedings of the NordicConference on Science and Technology Education: The Challengeof the Future (Karlslunde Strand, Denmark, May8-12, 1985). INSTITUTION Royal Danish School of EducationalStudies, Copenhagen (Denmark). SPONS AGENCY Nordic Culture Fund, Copenhagen(Denmark).; United Nations Educational, Scientific,and Cultural Organization, Paris (France). REPORT NO ISBN-87-88289-50-8 PUB DATE 8 May 85 NOTE 410p.; Document contains small print;drawings may not reproduce well. PUB TYPE Collected Works- Conference Proceedings (021) EDRS PRICE MF01/12C17 Plus Postage. DESCRIPTORS *Biological Sciences; ComputerUses in Education; Educational Trends; Energy Education;*Environmental Education; *International EducationalExchange; International Programs; MathematicsEducation; Models; *Physical Sciences; Scienceand Society; *Science Curriculum; ScienceEducation; *Science Instruction; Student Attitudes IDENTIFIERS *Nordic Countries ABSTRACT The Nordic Conference of 1985was convened for the purpose of fostering cooperation between scienceand technology educators within different fieldsand at different levels, with approximately 40 science and technologyeducators from Finland, Norway, Sweden, Denmark, India,the United States, and Yugoslavia participating. This report contains27 contributed papers fromthe conference. Some of the topics addressedinclude: (1) teaching with computers; (2) physics instruction; (3)theory of mathematics education; (4) UNESCO's activitiesin science -

More Real Applications for the ZX 81 and ZX Spectrum
More Real Applications for the ZX 81 and ZX Spectrum Macmillan Computing Books Assembly Language Programming for the BBC Microcomputer Ian Birnbaum Advanced Programming for the 16K ZX81 Mike Costello Microprocessors and Microcomputers - their use and programming Eric Huggins The Alien, Numbereater, and Other Programs for Personal Computers with notes on how they were written John Race Beginning BASIC Peter Gosling Continuing BASIC Peter Gosling Program Your Microcomputer in BASIC Peter Gosling Practical BASIC Programming Peter Gosling The Sinclair ZX81 - Programming for Real Applications Randle Hurley More Real Applications for the Spectrum and ZX81 Randle Hurley Assembly Language Assembled - for the Sinclair ZX81 Tony Woods Digital Techniques Noel Morris Microprocessor and Microcomputer Technology Noel Morris Understanding Microprocessors B. S. Walker Codes for Computers and Microprocessors P. Gosling and Q. Laarhoven Z80 Assembly Language Programming for Students Roger Hutty More Real Applications for the ZX81 and ZX Spectrum Randle Hurley M © Randle Hurley 1982 All rights reserved. No part of this publication may be reproduced or transmitted, in any form of by any means, without permission. Published by THE MACMILLAN PRESS LTD London and Basingstoke Company and representatives throughout the world ISBN 978-0-333-34543-6 ISBN 978-1-349-06604-9 (eBook) DOI 10.1007/978-1-349-06604-9 The paperback edition of this book is sold subject to the condition that it shall not, by way of trade or otherwise, be lent, resold, hired out, or otherwise circulated without the publisher's prior consent in any form of binding or cover other than that in which it is published and without a similar condition including this condition being imposed on the subsequent purchaser. -

CLONE WARS Get a Brazilian
April 2018 Issue 21 PLUS CLONE WARS Get a Brazilian.. Includes material MIND YOUR LANGUAGE not in the video Continued programming show! feature CONTENTS 16. CLONE WARS The Brazilian clones explored. 22. MIND YOUR LANGUAGE 12. OMNI 128HQ Spectrum languages. A new Speccy arrives. FEATURES GAME REVIEWS 4 News from 1987 Knight Lore 6 Find out what was happening back in 1987. Elixir Vitae 8 12 Isometric Games Grand Prix Championship 9 Knightlore and more. Viagem ao Centro da terra 14 16 Clone Wars Exploration of the Brazilian clones. Kung Fu Knights 20 24 Mind Your Language Sewer Rage 21 More languages from George. Dominator 22 32 Play Blackpool Report from the recent event. Spectres 23 36 Vega Games Wanted: Monty Mole 30 Games without instructions on the Vega. 3D Tunnel 31 38 Grumpy Ogre Retro adventuring and championship moaning. Gauntlet 34 42 Omni 128HQ Laptop A new Spectrum arrives. And more…. Page 2 www.thespectrumshow.co.uk EDITORIAL elcome to issue 21 and thank you W I was working on several things at the for taking the time to download and same time on two different comput- read it. ers. I was doing some video editing on As series seven of The Spectrum Show my main PC and at the same time checking emails and researching fu- comes to an end with a mammoth end say, I am impressed with it. It’s a Har- ture features on my little Macbook Air. of series special, the next series is al- lequin (Spectrum modern clone) main ready well underway in the planning Strangely, both required an update, so board fitted inside a new 48K style stages. -

Object Orientation Through the Lens of Computer Science Education with Some New Implications from Other Subjects Like the Humanities
Technische Universität München Fakultät für Informatik Fachgebiet Didaktik der Informatik Object-Oriented Programming through the Lens of Computer Science Education Marc-Pascal Berges Vollständiger Abdruck der von der Fakultät für Informatik der Technischen Universität München zur Erlangung des akademischen Grades eines Doktors der Naturwissenschaften (Dr. rer. nat.) genehmigten Dissertation. Vorsitzender: Univ.-Prof. Dr. Johann Schlichter Prüfer der Dissertation: 1. Univ.-Prof. Dr. Peter Hubwieser 2. Univ.-Prof. Dr. Torsten Brinda, Universität Duisburg-Essen Die Dissertation wurde am 07. April 2015 bei der Technischen Universität München eingereicht und durch die Fakultät für Informatik am 02. Juli 2015 angenommen. Abstract In recent years, the importance of the object-oriented paradigm has changed signifi- cantly. Initially it was mainly used in software engineering, but it is now being used more and more in education. This thesis applies methods of educational assessment and statistics to object-oriented programming and in doing so provides a broad overview of concepts, teaching methods, and the current state of research in this field of computer science. Recently, there have been various trends in introductory courses for object-oriented programming including objects-first and objects-later. Using current pedagogical concepts such as cognitive load theory, conceptual change, and self-directed learning in the context of this work, a teaching approach that dispenses almost entirely of instruction by teachers was developed. These minimally invasive programming courses (MIPC) were carried out in several passes in preliminary courses in the Department of Computer Science at the TU München. The students were confronted with a small programming task just before the first lecture. -
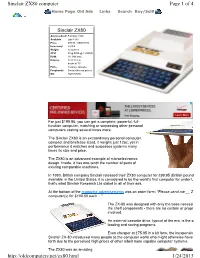
Page 1 of 4 Sinclair ZX80 Computer 1/24/2013
Sinclair ZX80 computer Page 1 of 4 Home Page Old Ads Links Search Buy/Sell! Sinclair ZX80 Anouncedced: February 1980 Available: Late 1980 Price: £99.95 / US$199.95 How many: 50,000 Weight: 12 ounces CPU: Zilog Z80A @ 3.25MHz RAM: 1K, 64K max Display: 22 X 32 text hooks to TV Ports: memory, cassette Peripherals: Sinclair thermal printer OS: ROM BASIC For just $199.95, you can get a complete, powerful, full- function computer, matching or surpassing other personal computers costing several times more. The Sinclair ZX80 is an extraordinary personal computer, compact and briefcase sized, it weighs just 12oz, yet in performance it matches and surpasses systems many times its size and price. The ZX80 is an advanced example of microelectronics design. Inside, it has one-tenth the number of parts of existing comparable machines. In 1980, British company Sinclair released their ZX80 computer for £99.95 (British pound available in the United States, it is considered to be the world's first computer for under U that's what Sinclair Research Ltd stated in all of their ads. At the bottom of the magazine advertisements was an order form: "Please send me __ ZX computer(s) for $199.95 each ..." The ZX-80 was designed with only the base necessit the shelf components - there are no custom or propri involved. An external cassette drive, typical of the era, is the o loading and saving programs. Even cheaper at £75.95 in a kit form, the inexpensive Sinclair ZX-80 introduced many people to the computer world who might otherwise have forth due to the perceived high prices of other albeit more capable computer systems. -

Issue #1 August 2015 Zxzine Table of Contents
zxzine Issue #1 August 2015 zxzine table of contents Published by: Timothy Swenson [email protected] [email protected] Editorial .......................... 1 ZXzine is published as a service to the Sinclair ZX81 community. Writers are invited to submit articles for publication. Readers The ZX80 and ZX81 are invited to submit article In The USA ........................... 1 ideas. Created using Open Source Tools: Plotting with Z88dk ........................... 5 OpenOffice Scribus Gimp SZ81 EightyOne ZX81 BASIC Compilers ........................... 6 Copyright 2015 Timothy Swenson Drawing a Line ........................... 8 Creative Commons License Attribution NonCommercial ShareAlike Astronomical Algorithms On You are free: The ZX81 ........................... 9 To copy, distribute, display, and perform the work. MicroSync Services ........................... 10 To make derivitive works. To redistribute the work. Editorial doing right. Ideas for article is invited, along with articles themselves. The topics of articles can be I've been a ZX81 user since the first was advertised anything that is ZX81 related. I'm hoping that the in the United States and used it for a number of ZX81 community will find the ezine interesting, years, including using it as much as I could in my entertaining and useful. first two years of college. Eventually moved on to the QL, but still liked the ZX81. A few years ago, I had the programming itch and decided to do a little The ZX80 and ZX81 assembly programming using emulators and ZX81 in the USA cross assemblers. Since then I've touched on C with Z88dk. What I like about the ZX81 is that I don't Sinclair Research Limited have to spend any time worrying about the user interface or making the program pretty. -

Didaktik Gama 192 Editoriale
Periodico di informazione sul mondo Sinclair e Spectrum N°4 Agosto - Settembre 2004 Copyleft 2004 Stefano Guida autore ed editore In questo numero: 1 - Didaktik Gama 192 Editoriale 2 - Spectrum... di sinistra? L'estate e' arrivata e come tutti Didaktik Gama che e' l'occasione come sempre per 2 - ZX81 gli anni, in questo periodo, le disponibile ad una cifra piuttosto ricordare a tutti voi che se volete 3 - Compatibilita' ZX Spectrum notizie e le novità ovviamente modica; ci sara' uno spazio scrivere un articolo per questa e altri cloni scarseggiano per poi riprendere dedicato alle curiosità alcune rivista potete farlo inviandolo 3 - Sir Clive ci riprova a pieno ritmo all'inizio delle quali anche divertenti, all'indirizzo: dell'autunno. articoli presi da internet e [email protected] . 3 - Vinili per Spectrum In questo numero affronteremo addirittura uno scritto da un Verrà pubblicato sul prossimo quindi gli argomenti che in appassionato lettore di questa numero con tanto di 4 - Minigame 2004 questi ultimi mesi hanno stessa rivista autore di un ringraziamenti per la 4 - Nuovi cloni popolato il web parlando anche programma molto utile nella collaborazione. dello ZX81. Una particolare gestione dei nastri ormai S.G. 4 - Damtape attenzione va al nuovo clone del deteriorati. Colgo quindi [email protected] 5 - Collegare un +2A/+3 via Scart 5 - QL Neeting 2004 5 - Mistrum Didaktik Gama 192 6 - Strane periferiche Come annunciato nel numero precedente, una Didaktik (che attualmente produce alcuni articoli 6 - Il clone del mese delle novità più discusse recentemente è il di componentistica e controllori di processi) alla 6 - Vignetta & ringraziamenti Didaktik Gama 192K. -

Vysoke´Ucˇenítechnicke´V Brneˇ
VYSOKE´ UCˇ ENI´ TECHNICKE´ V BRNEˇ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA INFORMACˇ NI´CH TECHNOLOGII´ U´ STAV POCˇ ´ITACˇ OVY´ CH SYSTE´ MU˚ FACULTY OF INFORMATION TECHNOLOGY DEPARTMENT OF COMPUTER SYSTEMS EMULA´TOR MALE´ HO DOMA´ CI´HO POCˇ ´ITACˇ E ZX SPECTRUM DIPLOMOVA´ PRA´ CE MASTER’S THESIS AUTOR PRA´ CE Bc. PETR Sˇ IMON AUTHOR BRNO 2012 VYSOKE´ UCˇ ENI´ TECHNICKE´ V BRNEˇ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA INFORMACˇ NI´CH TECHNOLOGII´ U´ STAV POCˇ ´ITACˇ OVY´ CH SYSTE´ MU˚ FACULTY OF INFORMATION TECHNOLOGY DEPARTMENT OF COMPUTER SYSTEMS EMULA´TOR MALE´ HO DOMA´ CI´HO POCˇ ´ITACˇ E ZX SPECTRUM ZX SPECTRUM SMALL HOME COMPUTER EMULATOR DIPLOMOVA´ PRA´ CE MASTER’S THESIS AUTOR PRA´ CE Bc. PETR Sˇ IMON AUTHOR VEDOUCI´ PRA´ CE Ing. RICHARD RU˚ Zˇ ICˇ KA, Ph.D. SUPERVISOR BRNO 2012 Abstrakt Osmibitový počítač ZX Spectrum vznikl pøed 30 lety. Ve své době zažil obrovský úspěch a dodnes má poèetnou základnu příznivcù, kteří stále vytvářejí nové aplikace a hry. Vznikají v¹ak i nová hardwarová rozšíření pro pøipojení moderních periferií, jako jsou IDE HDD, paměťové karty apod. Tato práce si dává za cíl navrhnout a postavit emulátor počítače ZX Spectrum, který bude založen na moderní technologii FPGA a bude používat moderní periferie jako VGA monitor, SD/MMC paměťové karty apod. Abstract Eight-bit computer ZX Spectrum has been created 30 years ago. It was extremely popular in its time and it has many fans till now, which still developing new application and games. There are also many new hardware extensions like IDE HDD driver, SD/MMC memory driver etc.