DOCSLIB.ORG

Sonobe Origami for Enriching Understanding of Geometric Concepts in Three Dimensions

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Sonobe Origami for Enriching Understanding of Geometric Concepts in Three Dimensions Sonobe Origami for enriching understanding of geometric concepts in three dimensions DONNA A. DIETZ American University Washington, D.C. Donna Dietz, American University Sonobe Origami for enriching understanding of geometric concepts in three dimensions St. Mary's College of Maryland November 7, 2015. MAA Section Meeting 3:15 pm -3:35 pm Goodpaster Hall Room 109 "Programs that take advantage of paper folding to teach mathematics are thriving in many parts of the world," according to the organizers of the MAA origami-themed Contributed Paper Session to be held at the JMM in January 2016. But, K-12 should not be having all the fun! In this talk, I will show some ways of stimulating student engagement using sonobe origami. These activities can be used in General Education mathematics "appreciation" courses or for Non-Euclidean Geometry for mathematics majors. Specifically, the goals are enriching student understanding of surface curvatures and helping them understand the duality of the regular polyhedra using these folded paper objects. Things to chat about... ● Construction overview and classroom hints ● Duality of regular polyhedra (aka Platonic Solids) ● Euler's χ for topological classification ● Angle deficit for topological classification ● Gauss-Bonnet Theorem ● Bonus Puzzle! Construction Basics ● tinyurl.com/sonobe ● I also have videos on YouTube ● for Gen Ed course- one class period ● students spend about an hour outside of class ● 30 pieces of paper per student ● chirality compatibility is a construction issue ● assembly is a learning experience for students The Paper I Use in Class: Pros and Cons ● No glue ● Only time for one large project rather ● No scissors than many small ones ● Straightedge and Compass is ● Object is more equivalent to folding complex than regular polyhedra ● Pride in crafting Make 30 of those Ok, Great! Now, what is this sonobe project good for? Duality of Regular Polyhedra mathforum.org Cube with Octahedron behance.net Icosahedron with Dodecahedron behance.net Tetrahedron is self dual math.brown.edu mathcraft.wonderhowto.com How much paper is that!? To build the basic object, consider the underlying icosahedron (20 sides) and count pyramids. Each side has a pyramid attached which uses 3 units. But each unit is used in two pyramids. 20*3/2 = 30 Other objects ● Tetrahedron: 4*3/2 = 6 units, but it's a cube! ● Octahedron: 8*3/2 = 12 units ● Icosahedron: 20*3/2 = 30 units ● Massive ball: (12x5)*3/2 = 90 units All of these objects are based off of an underlying triangular mesh frame. Euler's χ for topological classification Euler's χ for topological classification ● 6 vertices = v ● 9 edges = e ● 4 faces = f ● χ = v – e + f ● χ = 1 for single components with no holes maverick.inria.fr Euler's χ for topological classification ● 16 vertices = v ● 28 edges = e ● 14 faces = f ● 2 “blobs” = b ● χ = v – e + f - b ● χ = (16+14)–(28+2) = 0 for “donuts” Euler's χ for topological classification ● 8 vertices = v ● 12 edges = e ● 6 faces = f ● 1 “blob” = b ● χ = v – e + f - b ● χ = 8 – 12 + 6 – 1 = 1 for “spheres” mathcraft.wonderhowto.com Euler's χ for topological classification ● 6+8 vertices = v ● (3+3/2)*8 edges = e ● 8*3 faces = f ● 1 “blob” = b ● χ = v – e + f - b ● χ = 14 - 36 + 24 – 1 = 1 for “spheres” mathcraft.wonderhowto.com Euler's χ for topological classification ● 20 + 12 vertices = v ● (3+3/2)*20 edges = e ● 20*3 faces = f ● 1 “blob” = b ● χ = v – e + f - b ● χ = 32 - 90 + 60 – 1 = 1 for “spheres” Angle deficit for topological classification Angle deficit for topological classification “And now for something completely different...” Angle deficit for topological classification ● Imagine a flattened cube ● At each vertex, 90 degrees is “missing” ● 8 * 90 = 720 ● Total Angle Deficit is 720 mathcraft.wonderhowto.com Angle deficit for topological classification ● A flattened cube! ● At each vertex, 90 degrees is “missing” ● 8 * 90 = 720 ● Total Angle Deficit is 720 Cuboctahedron Template Cuboctahedron in 3D ● 12 vertices ● 60 degree deficit per ● 12*60=720 ● Total Angle Deficit is 720 Sonobe! ● 20 vertices with 90 degree deficit (elliptic curvature!) ● 12 vertices with -90 degree deficit (hyperbolic curvature) ● 20*90-12*90=720 But.... Total Angle Deficit = 4π * χ Gauss-Bonnet Theorem Gauss-Bonnet Theorem If we trace out a closed curve on a surface, the total enclosed Gauss curvature (total angle deficit) is 2π minus the total angle defect (angles of deflection) around the curve. Gauss-Bonnet simple example ● Total angle defect is zero. (This paper ribbon is a geodesic.) ● Each half of the sphere must have the same enclosed Gauss curvature. ● Total must be 4π ● Each half contains 2π Gauss-Bonnet simple example ● Total angle defect is zero. (This paper ribbon is a geodesic.) ● Each half of the can must have the same enclosed Gauss curvature. ● Total must be 4π ● Each half contains 2π Gauss-Bonnet simple example ● Total angle defect is zero. ● Each half of the cube must have the same enclosed Gauss curvature. ● Each half contains 2π ● Each vertex has π/2 Gauss-Bonnet example ● Total angle defect is: 2(180-72)+2(180-120) 336 ● 360-336=24 degrees ● Angle deficit: 360-(60+60+108+108) 24 degrees Gauss-Bonnet example ● Total angle defect is: 3(180-84) 288 ● 360-288=72 degrees ● Angle deficit: 3(360-60-60-108-108) 720 degrees Gauss-Bonnet example ● Total angle defect is: 5(180-120) 300 ● 360-300 = 60 degrees ● Angle deficit: 5(360-108-120-120) 60 degrees Gauss-Bonnet example ● Total angle defect is zero (geodesic!) ● 360 degrees is promised ● Angle deficit: 5(90)+(-90) 360 degrees Bonus Puzzle Use 3 colors, 10 pieces of each color. Try to make sure you get exactly one of each color on each pyramid. (Solve using a graph first.) Bonus Puzzle Solution http://www.donnadietz.com http://www.donnadietz.com/Origami.pdf [email protected] .
Load more

Recommended publications
  • How to Make an Origami Octahedron Ball
    How to make an Origami Octahedron Ball Introduction: These instructions will teach you how to make an origami octahedron. The ball is constructed by assembling 12 folded units together. A unit This is called a Sonobe unit, named after the person who invented them. The process of using identical units and assembling them in a pattern to create large, complex, beautiful structures is considered modular origami. This type of origami requires multiple sheets of paper to make a model. By varying the number of units, you can make several other shapes. A cube requires 6 units and an icosahedron requires 30. Time Frame: 30 minutes Materials: 2- 8.5”x11” sheets of paper (Multi-colored ball: use 3 different colored sheets of paper) Scissors Ruler (measures inches) Pencil Preparation: Make sure you have enough space and a flat surface to fold the origami. Procedure: Step 1. Cut 12 – 3”x3” square pieces of paper Note: The size of the squares depends on your preference of how large you want the ball to be. These instructions create a ball that fits in your hand. To save time, origami squares (4”x4”) can be used and step 1 skipped. 1.1. Draw 6 squares that are 3”x3” on a sheet of paper with the pencil and ruler. Note: For a multi-color effect, as depicted in these instructions, use 3 different colors of paper and cut 4 squares from each. 1.2.Stack the second sheet of paper behind the first. 1.3. Cut out 12 squares of paper with the scissors.
    [Show full text]
  • Sonobe Origami Units
    Sonobe Origami Units Crease paper down the middle Fold edges to center line and Fold top right and bottom left Fold triangles down to make and unfold unfold corners | do not let the sharper triangles | do not triangles cross crease lines cross the crease lines Fold along vertical crease lines Fold top left corner down to Fold bottom right corner up to Undo the last two folds right edge left edge Tuck upper left corner under Turn the paper over, crease Corners of one module ¯t into along dashed lines as shown to flap on opposite side and pockets of another A cube requires six modules repeat for lower right corner complete the module Sonobe modules also make many other polyhedra Where's the Math in Origami? Origami may not seem like it involves very much mathematics. Yes, origami involves symmetry. If we build a polyhedron then, sure, we encounter a shape from geometry. Is that as far as it goes? Do any interesting mathematical questions arise from the process of folding paper? Is there any deep mathematics in origami? Is the mathematics behind origami useful for anything other than making pretty decorations? People who spend time folding paper often ask themselves questions that are ultimately mathematical in nature. Is there a simpler procedure for folding a certain ¯gure? Where on the original square paper do the wings of a crane come from? What size paper should I use to make a chair to sit at the origami table I already made? Is it possible to make an origami beetle that has six legs and two antennae from a single square sheet of paper? Is there a precise procedure for folding a paper into ¯ve equal strips? In the last few decades, folders inspired by questions like these have revolutionized origami by bringing mathematical techniques to their art.
    [Show full text]
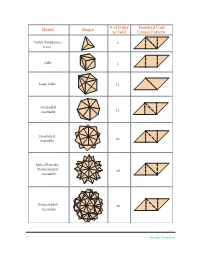
  • Sonobe Assembly Guide for a Few Polyhedra
    Model Shape # of Units Finished Unit to Fold Crease Pattern Toshie Takahama’s 3 Jewel Cube 6 Large Cube 12 Octahedral Assembly 12 Icosahedral Assembly 30 Spiked Pentakis Dodecahedral 60 Assembly Dodecahedral 90 Assembly 2 Sonobe Variations Sonobe Assembly Basics Sonobe assemblies are essentially “pyramidized” constructing a polyhedron, the key thing to re- polyhedra, each pyramid consisting of three So- member is that the diagonal ab of each Sonobe nobe units. The figure below shows a generic So- unit will lie along an edge of the polyhedron. nobe unit and how to form one pyramid. When a Pocket Tab Forming one Tab pyramid Pocket b A generic Sonobe unit representation Sonobe Assembly Guide for a Few Polyhedra 1. Toshie’s Jewel: Crease three finished units as tabs and pockets. This assembly is also sometimes explained in the table on page 2. Form a pyramid known as a Crane Egg. as above. Then turn the assembly upside down 2. Cube Assembly: Crease six finished units as and make another pyramid with the three loose explained in the table on page 2. Each face will be made up of 3 the center square of one unit and the tabs of two other units. 4 Do Steps 1 and 2 to form one face. Do Steps 3 and 4 to form one corner or vertex. Continue 1 2 interlocking in this manner to arrive at the finished cube. Sonobe Variations 3 3. Large Cube Assembly: Crease 12 finished units as explained on page 2. 5 6 3 The 12-unit large cube is the only assembly that does not involve pyramidizing.
    [Show full text]
  • The Geometry Junkyard: Origami
    Table of Contents Table of Contents 1 Origami 2 Origami The Japanese art of paper folding is obviously geometrical in nature. Some origami masters have looked at constructing geometric figures such as regular polyhedra from paper. In the other direction, some people have begun using computers to help fold more traditional origami designs. This idea works best for tree-like structures, which can be formed by laying out the tree onto a paper square so that the vertices are well separated from each other, allowing room to fold up the remaining paper away from the tree. Bern and Hayes (SODA 1996) asked, given a pattern of creases on a square piece of paper, whether one can find a way of folding the paper along those creases to form a flat origami shape; they showed this to be NP-complete. Related theoretical questions include how many different ways a given pattern of creases can be folded, whether folding a flat polygon from a square always decreases the perimeter, and whether it is always possible to fold a square piece of paper so that it forms (a small copy of) a given flat polygon. Krystyna Burczyk's Origami Gallery - regular polyhedra. The business card Menger sponge project. Jeannine Mosely wants to build a fractal cube out of 66048 business cards. The MIT Origami Club has already made a smaller version of the same shape. Cardahedra. Business card polyhedral origami. Cranes, planes, and cuckoo clocks. Announcement for a talk on mathematical origami by Robert Lang. Crumpling paper: states of an inextensible sheet. Cut-the-knot logo.
    [Show full text]
  • A Survey of Folding and Unfolding in Computational Geometry
    Combinatorial and Computational Geometry MSRI Publications Volume 52, 2005 A Survey of Folding and Unfolding in Computational Geometry ERIK D. DEMAINE AND JOSEPH O’ROURKE Abstract. We survey results in a recent branch of computational geome- try: folding and unfolding of linkages, paper, and polyhedra. Contents 1. Introduction 168 2. Linkages 168 2.1. Definitions and fundamental questions 168 2.2. Fundamental questions in 2D 171 2.3. Fundamental questions in 3D 175 2.4. Fundamental questions in 4D and higher dimensions 181 2.5. Protein folding 181 3. Paper 183 3.1. Categorization 184 3.2. Origami design 185 3.3. Origami foldability 189 3.4. Flattening polyhedra 191 4. Polyhedra 193 4.1. Unfolding polyhedra 193 4.2. Folding polygons into convex polyhedra 196 4.3. Folding nets into nonconvex polyhedra 199 4.4. Continuously folding polyhedra 200 5. Conclusion and Higher Dimensions 201 Acknowledgements 202 References 202 Demaine was supported by NSF CAREER award CCF-0347776. O’Rourke was supported by NSF Distinguished Teaching Scholars award DUE-0123154. 167 168 ERIKD.DEMAINEANDJOSEPHO’ROURKE 1. Introduction Folding and unfolding problems have been implicit since Albrecht D¨urer [1525], but have not been studied extensively in the mathematical literature until re- cently. Over the past few years, there has been a surge of interest in these problems in discrete and computational geometry. This paper gives a brief sur- vey of most of the work in this area. Related, shorter surveys are [Connelly and Demaine 2004; Demaine 2001; Demaine and Demaine 2002; O’Rourke 2000]. We are currently preparing a monograph on the topic [Demaine and O’Rourke ≥ 2005].
    [Show full text]
  • Arxiv:2105.14305V1 [Cs.CG] 29 May 2021
    Efficient Folding Algorithms for Regular Polyhedra ∗ Tonan Kamata1 Akira Kadoguchi2 Takashi Horiyama3 Ryuhei Uehara1 1 School of Information Science, Japan Advanced Institute of Science and Technology (JAIST), Ishikawa, Japan fkamata,[email protected] 2 Intelligent Vision & Image Systems (IVIS), Tokyo, Japan [email protected] 3 Faculty of Information Science and Technology, Hokkaido University, Hokkaido, Japan [email protected] Abstract We investigate the folding problem that asks if a polygon P can be folded to a polyhedron Q for given P and Q. Recently, an efficient algorithm for this problem has been developed when Q is a box. We extend this idea to regular polyhedra, also known as Platonic solids. The basic idea of our algorithms is common, which is called stamping. However, the computational complexities of them are different depending on their geometric properties. We developed four algorithms for the problem as follows. (1) An algorithm for a regular tetrahedron, which can be extended to a tetramonohedron. (2) An algorithm for a regular hexahedron (or a cube), which is much efficient than the previously known one. (3) An algorithm for a general deltahedron, which contains the cases that Q is a regular octahedron or a regular icosahedron. (4) An algorithm for a regular dodecahedron. Combining these algorithms, we can conclude that the folding problem can be solved pseudo-polynomial time when Q is a regular polyhedron and other related solid. Keywords: Computational origami folding problem pseudo-polynomial time algorithm regular poly- hedron (Platonic solids) stamping 1 Introduction In 1525, the German painter Albrecht D¨urerpublished his masterwork on geometry [5], whose title translates as \On Teaching Measurement with a Compass and Straightedge for lines, planes, and whole bodies." In the book, he presented each polyhedron by drawing a net, which is an unfolding of the surface of the polyhedron to a planar layout without overlapping by cutting along its edges.
    [Show full text]
  • Paper Pentasia: an Aperiodic Surface in Modular Origami
    Paper Pentasia: An Aperiodic Surface in Modular Origami a b Robert J. Lang ∗ and Barry Hayes † aLangorigami.com, Alamo, California, USA, bStanford University, Stanford, CA 2013-05-26 Origami, the Japanese art of paper-folding, has numerous connections to mathematics, but some of the most direct appear in the genre of modular origami. In modular origami, one folds many sheets into identical units (or a few types of unit), and then fits the units together into larger constructions, most often, some polyhedral form. Modular origami is a diverse and dynamic field, with many practitioners (see, e.g., [12, 3]). While most modular origami is created primarily for its artistic or decorative value, it can be used effectively in mathematics education to provide physical models of geometric forms ranging from the Platonic solids to 900-unit pentagon-hexagon-heptagon torii [5]. As mathematicians have expanded their catalog of interesting solids and surfaces, origami designers have followed not far behind, rendering mathematical forms via folding, a notable recent example being a level-3 Menger Sponge folded from 66,048 business cards by Jeannine Mosely and co-workers [10]. In some cases, the origami explorations themselves can lead to new mathematical structures and/or insights. Mosely’s developments of business-card modulars led to the discovery of a new fractal polyhedron with a novel connection to the famous Snowflake curve [11]. One of the most popular geometric mathematical objects has been the sets of aperiodic tilings developed by Roger Penrose [14, 15], which acquired new significance with the dis- covery of quasi-crystals, their three-dimensional analogs in the physical world, in 1982 by Daniel Schechtman, who was awarded the 2011 Nobel Prize in Chemistry for his discovery.
    [Show full text]
  • Universal Folding Pathways of Polyhedron Nets
    Universal folding pathways of polyhedron nets Paul M. Dodda, Pablo F. Damascenob, and Sharon C. Glotzera,b,c,d,1 aChemical Engineering Department, University of Michigan, Ann Arbor, MI 48109; bApplied Physics Program, University of Michigan, Ann Arbor, MI 48109; cDepartment of Materials Science and Engineering, University of Michigan, Ann Arbor, MI 48109; and dBiointerfaces Institute, University of Michigan, Ann Arbor, MI 48109 Contributed by Sharon C. Glotzer, June 6, 2018 (sent for review January 17, 2018; reviewed by Nuno Araujo and Andrew L. Ferguson) Low-dimensional objects such as molecular strands, ladders, and navigate, thermodynamically, from a denatured (unfolded) state sheets have intrinsic features that affect their propensity to fold to a natured (folded) one. Even after many decades of study, into 3D objects. Understanding this relationship remains a chal- however, a universal relationship between molecular sequence lenge for de novo design of functional structures. Using molecular and folded state—which could provide crucial insight into the dynamics simulations, we investigate the refolding of the 24 causes and potential treatments of many diseases—remains out possible 2D unfoldings (“nets”) of the three simplest Platonic of reach (11–13). shapes and demonstrate that attributes of a net’s topology— In this work, we study the thermodynamic foldability of 2D net compactness and leaves on the cutting graph—correlate nets for all five Platonic solids. Despite being the simplest and with thermodynamic folding propensity. To
    [Show full text]
  • Making an Origami Sonobe Octahedron
    Making an Origami Sonobe Octahedron Now that you have made a Sonobe unit and a Sonobe cube, you are ready to constuct a more complicated polyhedron. (We highly recommend building a cube before attempting to construct other polyhedra.) This handout will show you how to assemble twelve units into a small triakis octahedron. You can find instructions for making some other polyhedra online. To make the triakis octahedron, you can use any colour combination you like. In this example we use twelve units in three colours (four units of each colour). 1. Fold twelve Sonobe units (see the Making an Origami Sonobe Unit handout for instructions). Make an extra fold in each Sonobe unit by placing the unit with the side containing the X facing up and folding along the dotted line shown in the leftmost image below. 2. Assemble three units (one of each colour) as described in Step 2 of the Making an Origami Sonobe Cube handout to create a single corner, or pyramid, with three flaps (below, left). We are going to make more pyramids using these three flaps. Each new pyramid will also contain all three colours. 3. To make a second pyramid of three colours, choose a flap. We chose the purple flap, so we will add one new pink unit and one new blue unit to our construction. To add the new pink unit, insert a flap of the pink unit into the pocket of the chosen purple unit (above, centre). To add the new blue unit, insert a flap of the blue unit into the pocket of the new pink unit (shown by the white arrow above).
    [Show full text]
  • Sonobe Variations Ashley Shimabuku
    Sonobe Variations Ashley Shimabuku 1 Introduction This origami activity is a variation on the Sonobe unit activity. The students loved the original origami activity and they like how these variations are just as easy to build but look more complicated. The same kinds of questions can be asked about these Sonobe units. There is a worksheet included in the Paper Folding and Polyhedra paper. The polyhedra are built in the same fashion. So the stellated octahedron and stellated icosahedron can also be made using these variations. Additionally, the original Sonobe unit and the variations can be mixed and matched. There are two variations presented below the \bar" Sonobe and the \zig zag" Sonobe. There is a video with instructions [1] however it can be hard to follow. Instructions with pictures are given below. 2 Materials Required 1. Origami paper (two sided) 2. Diagram on how to make a Sonobe unit or variations on the Sonobe unit 3. Example of a constructed cube 3 Lesson Plan This activity can be done in a class period or less. If the students are familiar with the Sonobe unit it may take less time as the polyhedra are constructed in the same way. Students seem to like the variations slightly better than the original Sonobe as the variations look more complicated. The same counting questions can be asked and discussed with the students. Two sided origami paper is recommended as the color of backside of the paper is what makes the \bars" or \zig zag" pattern. 1 4 Instructions for Bar Variation (a) Step 1 Fold paper down the (b) Step 2 Fold edges to center (c) Step 3 Fold edges outward middle and unfold line and unfold (d) Step 4 Fold top left corner (e) Step 5 Tuck upper left corner (f) Step 6 Turn over and fold down to right edge, then fold top under flap on opposite side and bottom point straight up right corner down to left edge repeat for lower right corner (g) Finished 2 5 References 1.
    [Show full text]
  • Marvelous Modular Origami
    www.ATIBOOK.ir Marvelous Modular Origami www.ATIBOOK.ir Mukerji_book.indd 1 8/13/2010 4:44:46 PM Jasmine Dodecahedron 1 (top) and 3 (bottom). (See pages 50 and 54.) www.ATIBOOK.ir Mukerji_book.indd 2 8/13/2010 4:44:49 PM Marvelous Modular Origami Meenakshi Mukerji A K Peters, Ltd. Natick, Massachusetts www.ATIBOOK.ir Mukerji_book.indd 3 8/13/2010 4:44:49 PM Editorial, Sales, and Customer Service Office A K Peters, Ltd. 5 Commonwealth Road, Suite 2C Natick, MA 01760 www.akpeters.com Copyright © 2007 by A K Peters, Ltd. All rights reserved. No part of the material protected by this copyright notice may be reproduced or utilized in any form, electronic or mechanical, including photo- copying, recording, or by any information storage and retrieval system, without written permission from the copyright owner. Library of Congress Cataloging-in-Publication Data Mukerji, Meenakshi, 1962– Marvelous modular origami / Meenakshi Mukerji. p. cm. Includes bibliographical references. ISBN 978-1-56881-316-5 (alk. paper) 1. Origami. I. Title. TT870.M82 2007 736΄.982--dc22 2006052457 ISBN-10 1-56881-316-3 Cover Photographs Front cover: Poinsettia Floral Ball. Back cover: Poinsettia Floral Ball (top) and Cosmos Ball Variation (bottom). Printed in India 14 13 12 11 10 10 9 8 7 6 5 4 3 2 www.ATIBOOK.ir Mukerji_book.indd 4 8/13/2010 4:44:50 PM To all who inspired me and to my parents www.ATIBOOK.ir Mukerji_book.indd 5 8/13/2010 4:44:50 PM www.ATIBOOK.ir Contents Preface ix Acknowledgments x Photo Credits x Platonic & Archimedean Solids xi Origami Basics xii
    [Show full text]
  • PMA Day Workshop
    PMA Day Workshop March 25, 2017 Presenters: Jeanette McLeod Phil Wilson Sarah Mark Nicolette Rattenbury 1 Contents The Maths Craft Mission ...................................................................................................................... 4 About Maths Craft ............................................................................................................................ 6 Our Sponsors .................................................................................................................................... 7 The Möbius Strip .................................................................................................................................. 8 The Mathematics of the Möbius .................................................................................................... 10 One Edge, One Side .................................................................................................................... 10 Meet the Family ......................................................................................................................... 11 Making and Manipulating a Möbius Strip ...................................................................................... 13 Making a Möbius ........................................................................................................................ 13 Manipulating a Möbius .............................................................................................................. 13 The Heart of a Möbius ..............................................................................................................
    [Show full text]