14. Measuring Ultrashort Laser Pulses I: Autocorrelation the Dilemma the Goal: Measuring the Intensity and Phase Vs
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Near-Infrared Optical Modulation for Ultrashort Pulse Generation Employing Indium Monosulfide (Ins) Two-Dimensional Semiconductor Nanocrystals
nanomaterials Article Near-Infrared Optical Modulation for Ultrashort Pulse Generation Employing Indium Monosulfide (InS) Two-Dimensional Semiconductor Nanocrystals Tao Wang, Jin Wang, Jian Wu *, Pengfei Ma, Rongtao Su, Yanxing Ma and Pu Zhou * College of Advanced Interdisciplinary Studies, National University of Defense Technology, Changsha 410073, China; [email protected] (T.W.); [email protected] (J.W.); [email protected] (P.M.); [email protected] (R.S.); [email protected] (Y.M.) * Correspondence: [email protected] (J.W.); [email protected] (P.Z.) Received: 14 May 2019; Accepted: 3 June 2019; Published: 7 June 2019 Abstract: In recent years, metal chalcogenide nanomaterials have received much attention in the field of ultrafast lasers due to their unique band-gap characteristic and excellent optical properties. In this work, two-dimensional (2D) indium monosulfide (InS) nanosheets were synthesized through a modified liquid-phase exfoliation method. In addition, a film-type InS-polyvinyl alcohol (PVA) saturable absorber (SA) was prepared as an optical modulator to generate ultrashort pulses. The nonlinear properties of the InS-PVA SA were systematically investigated. The modulation depth and saturation intensity of the InS-SA were 5.7% and 6.79 MW/cm2, respectively. By employing this InS-PVA SA, a stable, passively mode-locked Yb-doped fiber laser was demonstrated. At the fundamental frequency, the laser operated at 1.02 MHz, with a pulse width of 486.7 ps, and the maximum output power was 1.91 mW. By adjusting the polarization states in the cavity, harmonic mode-locked phenomena were also observed. To our knowledge, this is the first time an ultrashort pulse output based on InS has been achieved. -

Von Mises' Frequentist Approach to Probability
Section on Statistical Education – JSM 2008 Von Mises’ Frequentist Approach to Probability Milo Schield1 and Thomas V. V. Burnham2 1 Augsburg College, Minneapolis, MN 2 Cognitive Systems, San Antonio, TX Abstract Richard Von Mises (1883-1953), the originator of the birthday problem, viewed statistics and probability theory as a science that deals with and is based on real objects rather than as a branch of mathematics that simply postulates relationships from which conclusions are derived. In this context, he formulated a strict Frequentist approach to probability. This approach is limited to observations where there are sufficient reasons to project future stability – to believe that the relative frequency of the observed attributes would tend to a fixed limit if the observations were continued indefinitely by sampling from a collective. This approach is reviewed. Some suggestions are made for statistical education. 1. Richard von Mises Richard von Mises (1883-1953) may not be well-known by statistical educators even though in 1939 he first proposed a problem that is today widely-known as the birthday problem.1 There are several reasons for this lack of recognition. First, he was educated in engineering and worked in that area for his first 30 years. Second, he published primarily in German. Third, his works in statistics focused more on theoretical foundations. Finally, his inductive approach to deriving the basic operations of probability is very different from the postulate-and-derive approach normally taught in introductory statistics. See Frank (1954) and Studies in Mathematics and Mechanics (1954) for a review of von Mises’ works. This paper is based on his two English-language books on probability: Probability, Statistics and Truth (1936) and Mathematical Theory of Probability and Statistics (1964). -

Pulse Shaping and Ultrashort Laser Pulse Filamentation for Applications in Extreme Nonlinear Optics Antonio Lotti
Pulse shaping and ultrashort laser pulse filamentation for applications in extreme nonlinear optics Antonio Lotti To cite this version: Antonio Lotti. Pulse shaping and ultrashort laser pulse filamentation for applications in extreme nonlinear optics. Optics [physics.optics]. Ecole Polytechnique X, 2012. English. pastel-00665670 HAL Id: pastel-00665670 https://pastel.archives-ouvertes.fr/pastel-00665670 Submitted on 2 Feb 2012 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. UNIVERSITA` DEGLI STUDI DELL’INSUBRIA ECOLE´ POLYTECHNIQUE THESIS SUBMITTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF PHILOSOPHIÆ DOCTOR IN PHYSICS Pulse shaping and ultrashort laser pulse filamentation for applications in extreme nonlinear optics. Antonio Lotti Date of defense: February 1, 2012 Examining committee: ∗ Advisor Daniele FACCIO Assistant Prof. at University of Insubria Advisor Arnaud COUAIRON Senior Researcher at CNRS Reviewer John DUDLEY Prof. at University of Franche-Comte´ Reviewer Danilo GIULIETTI Prof. at University of Pisa President Antonello DE MARTINO Senior Researcher at CNRS Paolo DI TRAPANI Associate Prof. at University of Insubria Alberto PAROLA Prof. at University of Insubria Luca TARTARA Assistant Prof. at University of Pavia ∗ current position: Reader in Physics at Heriot-Watt University, Edinburgh Abstract English abstract This thesis deals with numerical studies of the properties and applications of spatio-temporally coupled pulses, conical wavepackets and laser filaments, in strongly nonlinear processes, such as harmonic generation and pulse reshap- ing. -

Autocorrelation and Frequency-Resolved Optical Gating Measurements Based on the Third Harmonic Generation in a Gaseous Medium
Appl. Sci. 2015, 5, 136-144; doi:10.3390/app5020136 OPEN ACCESS applied sciences ISSN 2076-3417 www.mdpi.com/journal/applsci Article Autocorrelation and Frequency-Resolved Optical Gating Measurements Based on the Third Harmonic Generation in a Gaseous Medium Yoshinari Takao 1,†, Tomoko Imasaka 2,†, Yuichiro Kida 1,† and Totaro Imasaka 1,3,* 1 Department of Applied Chemistry, Graduate School of Engineering, Kyushu University, 744, Motooka, Nishi-ku, Fukuoka 819-0395, Japan; E-Mails: [email protected] (Y.T.); [email protected] (Y.K.) 2 Laboratory of Chemistry, Graduate School of Design, Kyushu University, 4-9-1, Shiobaru, Minami-ku, Fukuoka 815-8540, Japan; E-Mail: [email protected] 3 Division of Optoelectronics and Photonics, Center for Future Chemistry, Kyushu University, 744, Motooka, Nishi-ku, Fukuoka 819-0395, Japan † These authors contributed equally to this work. * Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel.: +81-92-802-2883; Fax: +81-92-802-2888. Academic Editor: Takayoshi Kobayashi Received: 7 April 2015 / Accepted: 3 June 2015 / Published: 9 June 2015 Abstract: A gas was utilized in producing the third harmonic emission as a nonlinear optical medium for autocorrelation and frequency-resolved optical gating measurements to evaluate the pulse width and chirp of a Ti:sapphire laser. Due to a wide frequency domain available for a gas, this approach has potential for use in measuring the pulse width in the optical (ultraviolet/visible) region beyond one octave and thus for measuring an optical pulse width less than 1 fs. -
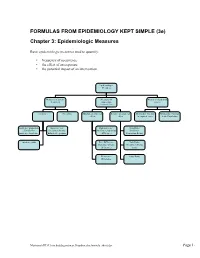
FORMULAS from EPIDEMIOLOGY KEPT SIMPLE (3E) Chapter 3: Epidemiologic Measures
FORMULAS FROM EPIDEMIOLOGY KEPT SIMPLE (3e) Chapter 3: Epidemiologic Measures Basic epidemiologic measures used to quantify: • frequency of occurrence • the effect of an exposure • the potential impact of an intervention. Epidemiologic Measures Measures of disease Measures of Measures of potential frequency association impact (“Measures of Effect”) Incidence Prevalence Absolute measures of Relative measures of Attributable Fraction Attributable Fraction effect effect in exposed cases in the Population Incidence proportion Incidence rate Risk difference Risk Ratio (Cumulative (incidence density, (Incidence proportion (Incidence Incidence, Incidence hazard rate, person- difference) Proportion Ratio) Risk) time rate) Incidence odds Rate Difference Rate Ratio (Incidence density (Incidence density difference) ratio) Prevalence Odds Ratio Difference Macintosh HD:Users:buddygerstman:Dropbox:eks:formula_sheet.doc Page 1 of 7 3.1 Measures of Disease Frequency No. of onsets Incidence Proportion = No. at risk at beginning of follow-up • Also called risk, average risk, and cumulative incidence. • Can be measured in cohorts (closed populations) only. • Requires follow-up of individuals. No. of onsets Incidence Rate = ∑person-time • Also called incidence density and average hazard. • When disease is rare (incidence proportion < 5%), incidence rate ≈ incidence proportion. • In cohorts (closed populations), it is best to sum individual person-time longitudinally. It can also be estimated as Σperson-time ≈ (average population size) × (duration of follow-up). Actuarial adjustments may be needed when the disease outcome is not rare. • In an open populations, Σperson-time ≈ (average population size) × (duration of follow-up). Examples of incidence rates in open populations include: births Crude birth rate (per m) = × m mid-year population size deaths Crude mortality rate (per m) = × m mid-year population size deaths < 1 year of age Infant mortality rate (per m) = × m live births No. -

Fundamental Frequency Detection
Fundamental Frequency Detection Jan Cernock´y,ˇ Valentina Hubeika cernocky|ihubeika @fit.vutbr.cz { } DCGM FIT BUT Brno Fundamental Frequency Detection Jan Cernock´y,ValentinaHubeika,DCGMFITBUTBrnoˇ 1/37 Agenda Fundamental frequency characteristics. • Issues. • Autocorrelation method, AMDF, NFFC. • Formant impact reduction. • Long time predictor. • Cepstrum. • Improvements in fundamental frequency detection. • Fundamental Frequency Detection Jan Cernock´y,ValentinaHubeika,DCGMFITBUTBrnoˇ 2/37 Recap – speech production and its model Fundamental Frequency Detection Jan Cernock´y,ValentinaHubeika,DCGMFITBUTBrnoˇ 3/37 Introduction Fundamental frequency, pitch, is the frequency vocal cords oscillate on: F . • 0 The period of fundamental frequency, (pitch period) is T = 1 . • 0 F0 The term “lag” denotes the pitch period expressed in samples : L = T Fs, where Fs • 0 is the sampling frequency. Fundamental Frequency Detection Jan Cernock´y,ValentinaHubeika,DCGMFITBUTBrnoˇ 4/37 Fundamental Frequency Utilization speech synthesis – melody generation. • coding • – in simple encoding such as LPC, reduction of the bit-stream can be reached by separate transfer of the articulatory tract parameters, energy, voiced/unvoiced sound flag and pitch F0. – in more complex encoders (such as RPE-LTP or ACELP in the GSM cell phones) long time predictor LTP is used. LPT is a filter with a “long” impulse response which however contains only few non-zero components. Fundamental Frequency Detection Jan Cernock´y,ValentinaHubeika,DCGMFITBUTBrnoˇ 5/37 Fundamental Frequency Characteristics F takes the values from 50 Hz (males) to 400 Hz (children), with Fs=8000 Hz these • 0 frequencies correspond to the lags L=160 to 20 samples. It can be seen, that with low values F0 approaches the frame length (20 ms, which corresponds to 160 samples). -

Pearson-Fisher Chi-Square Statistic Revisited
Information 2011 , 2, 528-545; doi:10.3390/info2030528 OPEN ACCESS information ISSN 2078-2489 www.mdpi.com/journal/information Communication Pearson-Fisher Chi-Square Statistic Revisited Sorana D. Bolboac ă 1, Lorentz Jäntschi 2,*, Adriana F. Sestra ş 2,3 , Radu E. Sestra ş 2 and Doru C. Pamfil 2 1 “Iuliu Ha ţieganu” University of Medicine and Pharmacy Cluj-Napoca, 6 Louis Pasteur, Cluj-Napoca 400349, Romania; E-Mail: [email protected] 2 University of Agricultural Sciences and Veterinary Medicine Cluj-Napoca, 3-5 M ănăş tur, Cluj-Napoca 400372, Romania; E-Mails: [email protected] (A.F.S.); [email protected] (R.E.S.); [email protected] (D.C.P.) 3 Fruit Research Station, 3-5 Horticultorilor, Cluj-Napoca 400454, Romania * Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel: +4-0264-401-775; Fax: +4-0264-401-768. Received: 22 July 2011; in revised form: 20 August 2011 / Accepted: 8 September 2011 / Published: 15 September 2011 Abstract: The Chi-Square test (χ2 test) is a family of tests based on a series of assumptions and is frequently used in the statistical analysis of experimental data. The aim of our paper was to present solutions to common problems when applying the Chi-square tests for testing goodness-of-fit, homogeneity and independence. The main characteristics of these three tests are presented along with various problems related to their application. The main problems identified in the application of the goodness-of-fit test were as follows: defining the frequency classes, calculating the X2 statistic, and applying the χ2 test. -

STAT 830 the Basics of Nonparametric Models The
STAT 830 The basics of nonparametric models The Empirical Distribution Function { EDF The most common interpretation of probability is that the probability of an event is the long run relative frequency of that event when the basic experiment is repeated over and over independently. So, for instance, if X is a random variable then P (X ≤ x) should be the fraction of X values which turn out to be no more than x in a long sequence of trials. In general an empirical probability or expected value is just such a fraction or average computed from the data. To make this precise, suppose we have a sample X1;:::;Xn of iid real valued random variables. Then we make the following definitions: Definition: The empirical distribution function, or EDF, is n 1 X F^ (x) = 1(X ≤ x): n n i i=1 This is a cumulative distribution function. It is an estimate of F , the cdf of the Xs. People also speak of the empirical distribution of the sample: n 1 X P^(A) = 1(X 2 A) n i i=1 ^ This is the probability distribution whose cdf is Fn. ^ Now we consider the qualities of Fn as an estimate, the standard error of the estimate, the estimated standard error, confidence intervals, simultaneous confidence intervals and so on. To begin with we describe the best known summaries of the quality of an estimator: bias, variance, mean squared error and root mean squared error. Bias, variance, MSE and RMSE There are many ways to judge the quality of estimates of a parameter φ; all of them focus on the distribution of the estimation error φ^−φ. -

Approximate Maximum Likelihood Method for Frequency Estimation
Statistica Sinica 10(2000), 157-171 APPROXIMATE MAXIMUM LIKELIHOOD METHOD FOR FREQUENCY ESTIMATION Dawei Huang Queensland University of Technology Abstract: A frequency can be estimated by few Discrete Fourier Transform (DFT) coefficients, see Rife and Vincent (1970), Quinn (1994, 1997). This approach is computationally efficient. However, the statistical efficiency of the estimator de- pends on the location of the frequency. In this paper, we explain this approach from a point of view of an Approximate Maximum Likelihood (AML) method. Then we enhance the efficiency of this method by using more DFT coefficients. Compared to 30% and 61% efficiency in the worst cases in Quinn (1994) and Quinn (1997), respectively, we show that if 13 or 25 DFT coefficients are used, AML will achieve at least 90% or 95% efficiency for all frequency locations. Key words and phrases: Approximate Maximum Likelihood, discrete Fourier trans- form, efficiency, fast algorithm, frequency estimation, semi-sufficient statistics. 1. Introduction A model that has been discussed widely in Time Series Analysis and Signal Processing is the following: xt = Acos(tω + φ)+ut,t=0,...,T − 1, (1) where 0 <A,0 <ω<π,and {ut} is a stationary sequence satisfying certain conditions to be specified later. The objective is to estimate the frequency ω from the observations {xt}. After obtaining an estimator of the frequency, the amplitude A and the phase φ can be estimated by a standard linear least squares method. Two topics have been of interest in the study of this model: estimation efficiency and computational complexity. Following the idea of Best Asymp- totic Normal estimation (BAN), the efficiency hereafter is measured by the ratio of the Cramer - Rao Bound (CRB) for unbiased estimators over the variance of the asymptotic distribution of the estimator. -

Early-Stage Dynamics of Chloride Ion–Pumping Rhodopsin Revealed by a Femtosecond X-Ray Laser
Early-stage dynamics of chloride ion–pumping rhodopsin revealed by a femtosecond X-ray laser Ji-Hye Yuna,1, Xuanxuan Lib,c,1, Jianing Yued, Jae-Hyun Parka, Zeyu Jina, Chufeng Lie, Hao Hue, Yingchen Shib,c, Suraj Pandeyf, Sergio Carbajog, Sébastien Boutetg, Mark S. Hunterg, Mengning Liangg, Raymond G. Sierrag, Thomas J. Laneg, Liang Zhoud, Uwe Weierstalle, Nadia A. Zatsepine,h, Mio Ohkii, Jeremy R. H. Tamei, Sam-Yong Parki, John C. H. Spencee, Wenkai Zhangd, Marius Schmidtf,2, Weontae Leea,2, and Haiguang Liub,d,2 aDepartment of Biochemistry, College of Life Sciences and Biotechnology, Yonsei University, Seodaemun-gu, 120-749 Seoul, South Korea; bComplex Systems Division, Beijing Computational Science Research Center, Haidian, 100193 Beijing, People’s Republic of China; cDepartment of Engineering Physics, Tsinghua University, 100086 Beijing, People’s Republic of China; dDepartment of Physics, Beijing Normal University, Haidian, 100875 Beijing, People’s Republic of China; eDepartment of Physics, Arizona State University, Tempe, AZ 85287; fPhysics Department, University of Wisconsin, Milwaukee, Milwaukee, WI 53201; gLinac Coherent Light Source, Stanford Linear Accelerator Center National Accelerator Laboratory, Menlo Park, CA 94025; hDepartment of Chemistry and Physics, Australian Research Council Centre of Excellence in Advanced Molecular Imaging, La Trobe Institute for Molecular Science, La Trobe University, Melbourne, VIC 3086, Australia; and iDrug Design Laboratory, Graduate School of Medical Life Science, Yokohama City University, 230-0045 Yokohama, Japan Edited by Nicholas K. Sauter, Lawrence Berkeley National Laboratory, Berkeley, CA, and accepted by Editorial Board Member Axel T. Brunger February 21, 2021 (received for review September 30, 2020) Chloride ion–pumping rhodopsin (ClR) in some marine bacteria uti- an acceptor aspartate (13–15). -

Sketching for M-Estimators: a Unified Approach to Robust Regression
Sketching for M-Estimators: A Unified Approach to Robust Regression Kenneth L. Clarkson∗ David P. Woodruffy Abstract ing algorithm often results, since a single pass over A We give algorithms for the M-estimators minx kAx − bkG, suffices to compute SA. n×d n n where A 2 R and b 2 R , and kykG for y 2 R is specified An important property of many of these sketching ≥0 P by a cost function G : R 7! R , with kykG ≡ i G(yi). constructions is that S is a subspace embedding, meaning d The M-estimators generalize `p regression, for which G(x) = that for all x 2 R , kSAxk ≈ kAxk. (Here the vector jxjp. We first show that the Huber measure can be computed norm is generally `p for some p.) For the regression up to relative error in O(nnz(A) log n + poly(d(log n)=")) d time, where nnz(A) denotes the number of non-zero entries problem of minimizing kAx − bk with respect to x 2 R , of the matrix A. Huber is arguably the most widely used for inputs A 2 Rn×d and b 2 Rn, a minor extension of M-estimator, enjoying the robustness properties of `1 as well the embedding condition implies S preserves the norm as the smoothness properties of ` . 2 of the residual vector Ax − b, that is kS(Ax − b)k ≈ We next develop algorithms for general M-estimators. kAx − bk, so that a vector x that makes kS(Ax − b)k We analyze the M-sketch, which is a variation of a sketch small will also make kAx − bk small. -

The Science and Applications of Ultrafast, Ultraintense Lasers
THE SCIENCE AND APPLICATIONS OF ULTRAFAST, ULTRAINTENSE LASERS: Opportunities in science and technology using the brightest light known to man A report on the SAUUL workshop held, June 17-19, 2002 THE SCIENCE AND APPLICATIONS OF ULTRAFAST, ULTRAINTENSE LASERS (SAUUL) A report on the SAUUL workshop, held in Washington DC, June 17-19, 2002 Workshop steering committee: Philip Bucksbaum (University of Michigan) Todd Ditmire (University of Texas) Louis DiMauro (Brookhaven National Laboratory) Joseph Eberly (University of Rochester) Richard Freeman (University of California, Davis) Michael Key (Lawrence Livermore National Laboratory) Wim Leemans (Lawrence Berkeley National Laboratory) David Meyerhofer (LLE, University of Rochester) Gerard Mourou (CUOS, University of Michigan) Martin Richardson (CREOL, University of Central Florida) 2 Table of Contents Table of Contents . 3 Executive Summary . 5 1. Introduction . 7 1.1 Overview . 7 1.2 Summary . 8 1.3 Scientific Impact Areas . 9 1.4 The Technology of UULs and its impact. .13 1.5 Grand Challenges. .15 2. Scientific Opportunities Presented by Research with Ultrafast, Ultraintense Lasers . .17 2.1 Basic High-Field Science . .18 2.2 Ultrafast X-ray Generation and Applications . .23 2.3 High Energy Density Science and Lab Astrophysics . .29 2.4 Fusion Energy and Fast Ignition. .34 2.5 Advanced Particle Acceleration and Ultrafast Nuclear Science . .40 3. Advanced UUL Technology . .47 3.1 Overview . .47 3.2 Important Research Areas in UUL Development. .48 3.3 New Architectures for Short Pulse Laser Amplification . .51 4. Present State of UUL Research Worldwide . .53 5. Conclusions and Findings . .61 Appendix A: A Plan for Organizing the UUL Community in the United States .