DOCSLIB.ORG

Descriptive Statistics Frequency Distributions and Their Graphs

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Descriptive Statistics Frequency Distributions and Their Graphs Chapter 2 Descriptive Statistics § 2.1 Frequency Distributions and Their Graphs Frequency Distributions A frequency distribution is a table that shows classes or intervals of data with a count of the number in each class. The frequency f of a class is the number of data points in the class. Class Frequency, f 1 – 4 4 LowerUpper Class 5 – 8 5 Limits 9 – 12 3 Frequencies 13 – 16 4 17 – 20 2 Larson & Farber, Elementary Statistics: Picturing the World , 3e 3 1 Frequency Distributions The class width is the distance between lower (or upper) limits of consecutive classes. Class Frequency, f 1 – 4 4 5 – 1 = 4 5 – 8 5 9 – 5 = 4 9 – 12 3 13 – 9 = 4 13 – 16 4 17 – 13 = 4 17 – 20 2 The class width is 4. The range is the difference between the maximum and minimum data entries. Larson & Farber, Elementary Statistics: Picturing the World , 3e 4 Constructing a Frequency Distribution Guidelines 1. Decide on the number of classes to include. The number of classes should be between 5 and 20; otherwise, it may be difficult to detect any patterns. 2. Find the class width as follows. Determine the range of the data, divide the range by the number of classes, and round up to the next convenient number. 3. Find the class limits. You can use the minimum entry as the lower limit of the first class. To find the remaining lower limits, add the class width to the lower limit of the preceding class. Then find the upper class limits. 4. Make a tally mark for each data entry in the row of the appropriate class. 5. Count the tally marks to find the total frequency f for each class. Larson & Farber, Elementary Statistics: Picturing the World , 3e 5 Constructing a Frequency Distribution Example: The following data represents the ages of 30 students in a statistics class. Construct a frequency distribution that has five classes. Ages of Students 18 20 21 27 29 20 19 30 32 19 34 19 24 29 18 37 38 22 30 39 32 44 33 46 54 49 18 51 21 21 Continued. Larson & Farber, Elementary Statistics: Picturing the World , 3e 6 2 Constructing a Frequency Distribution Example continued: 1. The number of classes (5) is stated in the problem. 2. The minimum data entry is 18 and maximum entry is 54, so the range is 36. Divide the range by the number of classes to find the class width. Class width = 36 = 7.2 Round up to 8. 5 Continued. Larson & Farber, Elementary Statistics: Picturing the World , 3e 7 Constructing a Frequency Distribution Example continued: 3. The minimum data entry of 18 may be used for the lower limit of the first class. To find the lower class limits of the remaining classes, add the width (8) to each lower limit. The lower class limits are 18, 26, 34, 42, and 50. The upper class limits are 25, 33, 41, 49, and 57. 4. Make a tally mark for each data entry in the appropriate class. 5. The number of tally marks for a class is the frequency for that class. Continued. Larson & Farber, Elementary Statistics: Picturing the World , 3e 8 Constructing a Frequency Distribution Example continued: Number of Ages students Ages of Students Class Tally Frequency, f 18 – 25 13 26 – 33 8 34 – 41 4 42 – 49 3 Check that the 50 – 57 2 sum equals the number in the ∑f = 30 sample. Larson & Farber, Elementary Statistics: Picturing the World , 3e 9 3 Midpoint The midpoint of a class is the sum of the lower and upper limits of the class divided by two. The midpoint is sometimes called the class mark . (Lower class limit) + (Upper class limit) Midpoint = 2 Class Frequency, f Midpoint 1 – 4 4 2.5 1 + 4 5 Midpoint = = = 2.5 2 2 Larson & Farber, Elementary Statistics: Picturing the World , 3e 10 Midpoint Example : Find the midpoints for the “Ages of Students” frequency distribution. Ages of Students Class Frequency, f Midpoint 18 + 25 = 43 18 – 25 13 21.5 43 ÷ 2 = 21.5 26 – 33 8 29.5 34 – 41 4 37.5 42 – 49 3 45.5 50 – 57 2 53.5 ∑f = 30 Larson & Farber, Elementary Statistics: Picturing the World , 3e 11 Relative Frequency The relative frequency of a class is the portion or percentage of the data that falls in that class. To find the relative frequency of a class, divide the frequency f by the sample size n. Class frequency f Relative frequency = = Sample size n Relative Class Frequency, f Frequency 1 – 4 4 0.222 ∑f = 18 Relative frequency = f = 4 ≈ 0.222 n 18 Larson & Farber, Elementary Statistics: Picturing the World , 3e 12 4 Relative Frequency Example : Find the relative frequencies for the “Ages of Students” frequency distribution. Relative Portion of Class Frequency, f Frequency students 18 – 25 13 0.433 f 13 = 26 – 33 8 0.267 n 30 34 – 41 4 0.133 ≈ 0.433 42 – 49 3 0.1 50 – 57 2 0.067 f ∑f = 30 ∑ = 1 n Larson & Farber, Elementary Statistics: Picturing the World , 3e 13 Cumulative Frequency The cumulative frequency of a class is the sum of the frequency for that class and all the previous classes. Ages of Students Cumulative Class Frequency, f Frequency 18 – 25 13 13 26 – 33 + 8 21 34 – 41 + 4 25 42 – 49 + 3 28 Total number of 50 – 57+ 2 30 students ∑f = 30 Larson & Farber, Elementary Statistics: Picturing the World , 3e 14 Frequency Histogram A frequency histogram is a bar graph that represents the frequency distribution of a data set. 1. The horizontal scale is quantitative and measures the data values. 2. The vertical scale measures the frequencies of the classes. 3. Consecutive bars must touch. Class boundaries are the numbers that separate the classes without forming gaps between them. The horizontal scale of a histogram can be marked with either the class boundaries or the midpoints. Larson & Farber, Elementary Statistics: Picturing the World , 3e 15 5 Class Boundaries Example : Find the class boundaries for the “Ages of Students” frequency distribution. Ages of Students Class Class Frequency, f Boundaries The distance from the 18 – 25 13 17.5 − 25.5 upper limit of the first class to the lower limit 26 – 33 8 25.5 − 33.5 of the second class is 1. 34 – 41 4 33.5 − 41.5 42 – 49 3 41.5 − 49.5 Half this distance 50 – 57 2 49.5 − 57.5 is 0.5. ∑f = 30 Larson & Farber, Elementary Statistics: Picturing the World , 3e 16 Frequency Histogram Example : Draw a frequency histogram for the “Ages of Students” frequency distribution. Use the class boundaries. 14 13 Ages of Students 12 10 8 8 f 6 4 4 3 2 2 0 17.5 25.5 33.5 41.5 49.5 57.5 Broken axis Age (in years) Larson & Farber, Elementary Statistics: Picturing the World , 3e 17 Frequency Polygon A frequency polygon is a line graph that emphasizes the continuous change in frequencies. 14 Ages of Students 12 10 8 Line is extended to the x-axis. f 6 4 2 0 13.5 21.5 29.5 37.5 45.5 53.5 61.5 Broken axis Age (in years) Midpoints Larson & Farber, Elementary Statistics: Picturing the World , 3e 18 6 Relative Frequency Histogram A relative frequency histogram has the same shape and the same horizontal scale as the corresponding frequency histogram. 0.5 0.433 0.4 Ages of Students 0.3 0.267 0.2 0.133 0.1 Relative frequency 0.1 0.067 (portion students) of 0 17.5 25.5 33.5 41.5 49.5 57.5 Age (in years) Larson & Farber, Elementary Statistics: Picturing the World , 3e 19 Cumulative Frequency Graph A cumulative frequency graph or ogive , is a line graph that displays the cumulative frequency of each class at its upper class boundary. 30 Ages of Students 24 The graph ends at 18 the upper 12 boundary of the last class. 6 (portion students) of Cumulative frequency 0 17.5 25.5 33.5 41.5 49.5 57.5 Age (in years) Larson & Farber, Elementary Statistics: Picturing the World , 3e 20 § 2.2 More Graphs and Displays 7 Stem-and-Leaf Plot In a stem-and-leaf plot , each number is separated into a stem (usually the entry’s leftmost digits) and a leaf (usually the rightmost digit). This is an example of exploratory data analysis . Example : The following data represents the ages of 30 students in a statistics class. Display the data in a stem-and-leaf plot. Ages of Students 18 20 21 27 29 20 19 30 32 19 34 19 24 29 18 37 38 22 30 39 32 44 33 46 54 49 18 51 21 21 Continued. Larson & Farber, Elementary Statistics: Picturing the World , 3e 22 Stem-and-Leaf Plot Ages of Students Key: 1|8 = 18 1 8 8 8 9 9 9 2 0 0 1 1 1 2 4 7 9 9 Most of the values lie between 20 3 0 0 2 2 3 4 7 8 9 and 39. 4 4 6 9 5 1 4 This graph allows us to see the shape of the data as well as the actual values. Larson & Farber, Elementary Statistics: Picturing the World , 3e 23 Stem-and-Leaf Plot Example : Construct a stem-and-leaf plot that has two lines for each stem. Ages of Students 1 Key: 1|8 = 18 1 8 8 8 9 9 9 2 0 0 1 1 1 2 4 2 7 9 9 3 0 0 2 2 3 4 3 7 8 9 From this graph, we can conclude 4 4 that more than 50% of the data lie 4 6 9 between 20 and 34.
Load more

Recommended publications
  • Von Mises' Frequentist Approach to Probability
    Section on Statistical Education – JSM 2008 Von Mises’ Frequentist Approach to Probability Milo Schield1 and Thomas V. V. Burnham2 1 Augsburg College, Minneapolis, MN 2 Cognitive Systems, San Antonio, TX Abstract Richard Von Mises (1883-1953), the originator of the birthday problem, viewed statistics and probability theory as a science that deals with and is based on real objects rather than as a branch of mathematics that simply postulates relationships from which conclusions are derived. In this context, he formulated a strict Frequentist approach to probability. This approach is limited to observations where there are sufficient reasons to project future stability – to believe that the relative frequency of the observed attributes would tend to a fixed limit if the observations were continued indefinitely by sampling from a collective. This approach is reviewed. Some suggestions are made for statistical education. 1. Richard von Mises Richard von Mises (1883-1953) may not be well-known by statistical educators even though in 1939 he first proposed a problem that is today widely-known as the birthday problem.1 There are several reasons for this lack of recognition. First, he was educated in engineering and worked in that area for his first 30 years. Second, he published primarily in German. Third, his works in statistics focused more on theoretical foundations. Finally, his inductive approach to deriving the basic operations of probability is very different from the postulate-and-derive approach normally taught in introductory statistics. See Frank (1954) and Studies in Mathematics and Mechanics (1954) for a review of von Mises’ works. This paper is based on his two English-language books on probability: Probability, Statistics and Truth (1936) and Mathematical Theory of Probability and Statistics (1964).
    [Show full text]
  • Autocorrelation and Frequency-Resolved Optical Gating Measurements Based on the Third Harmonic Generation in a Gaseous Medium
    Appl. Sci. 2015, 5, 136-144; doi:10.3390/app5020136 OPEN ACCESS applied sciences ISSN 2076-3417 www.mdpi.com/journal/applsci Article Autocorrelation and Frequency-Resolved Optical Gating Measurements Based on the Third Harmonic Generation in a Gaseous Medium Yoshinari Takao 1,†, Tomoko Imasaka 2,†, Yuichiro Kida 1,† and Totaro Imasaka 1,3,* 1 Department of Applied Chemistry, Graduate School of Engineering, Kyushu University, 744, Motooka, Nishi-ku, Fukuoka 819-0395, Japan; E-Mails: [email protected] (Y.T.); [email protected] (Y.K.) 2 Laboratory of Chemistry, Graduate School of Design, Kyushu University, 4-9-1, Shiobaru, Minami-ku, Fukuoka 815-8540, Japan; E-Mail: [email protected] 3 Division of Optoelectronics and Photonics, Center for Future Chemistry, Kyushu University, 744, Motooka, Nishi-ku, Fukuoka 819-0395, Japan † These authors contributed equally to this work. * Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel.: +81-92-802-2883; Fax: +81-92-802-2888. Academic Editor: Takayoshi Kobayashi Received: 7 April 2015 / Accepted: 3 June 2015 / Published: 9 June 2015 Abstract: A gas was utilized in producing the third harmonic emission as a nonlinear optical medium for autocorrelation and frequency-resolved optical gating measurements to evaluate the pulse width and chirp of a Ti:sapphire laser. Due to a wide frequency domain available for a gas, this approach has potential for use in measuring the pulse width in the optical (ultraviolet/visible) region beyond one octave and thus for measuring an optical pulse width less than 1 fs.
    [Show full text]
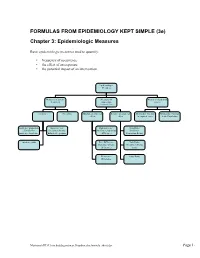
  • FORMULAS from EPIDEMIOLOGY KEPT SIMPLE (3E) Chapter 3: Epidemiologic Measures
    FORMULAS FROM EPIDEMIOLOGY KEPT SIMPLE (3e) Chapter 3: Epidemiologic Measures Basic epidemiologic measures used to quantify: • frequency of occurrence • the effect of an exposure • the potential impact of an intervention. Epidemiologic Measures Measures of disease Measures of Measures of potential frequency association impact (“Measures of Effect”) Incidence Prevalence Absolute measures of Relative measures of Attributable Fraction Attributable Fraction effect effect in exposed cases in the Population Incidence proportion Incidence rate Risk difference Risk Ratio (Cumulative (incidence density, (Incidence proportion (Incidence Incidence, Incidence hazard rate, person- difference) Proportion Ratio) Risk) time rate) Incidence odds Rate Difference Rate Ratio (Incidence density (Incidence density difference) ratio) Prevalence Odds Ratio Difference Macintosh HD:Users:buddygerstman:Dropbox:eks:formula_sheet.doc Page 1 of 7 3.1 Measures of Disease Frequency No. of onsets Incidence Proportion = No. at risk at beginning of follow-up • Also called risk, average risk, and cumulative incidence. • Can be measured in cohorts (closed populations) only. • Requires follow-up of individuals. No. of onsets Incidence Rate = ∑person-time • Also called incidence density and average hazard. • When disease is rare (incidence proportion < 5%), incidence rate ≈ incidence proportion. • In cohorts (closed populations), it is best to sum individual person-time longitudinally. It can also be estimated as Σperson-time ≈ (average population size) × (duration of follow-up). Actuarial adjustments may be needed when the disease outcome is not rare. • In an open populations, Σperson-time ≈ (average population size) × (duration of follow-up). Examples of incidence rates in open populations include: births Crude birth rate (per m) = × m mid-year population size deaths Crude mortality rate (per m) = × m mid-year population size deaths < 1 year of age Infant mortality rate (per m) = × m live births No.
    [Show full text]
  • Programming in Stata
    Programming and Post-Estimation • Bootstrapping • Monte Carlo • Post-Estimation Simulation (Clarify) • Extending Clarify to Other Models – Censored Probit Example What is Bootstrapping? • A computer-simulated nonparametric technique for making inferences about a population parameter based on sample statistics. • If the sample is a good approximation of the population, the sampling distribution of interest can be estimated by generating a large number of new samples from the original. • Useful when no analytic formula for the sampling distribution is available. B 2 ˆ B B b How do I do it? SE B = s(x )- s(x )/ B /(B -1) å[ åb =1 ] b=1 1. Obtain a Sample from the population of interest. Call this x = (x1, x2, … , xn). 2. Re-sample based on x by randomly sampling with replacement from it. 3. Generate many such samples, x1, x2, …, xB – each of length n. 4. Estimate the desired parameter in each sample, s(x1), s(x2), …, s(xB). 5. For instance the bootstrap estimate of the standard error is the standard deviation of the bootstrap replications. Example: Standard Error of a Sample Mean Canned in Stata use "I:\general\PRISM Programming\auto.dta", clear Type: sum mpg Example: Standard Error of a Sample Mean Canned in Stata Type: bootstrap "summarize mpg" r(mean), reps(1000) » 21.2973±1.96*.6790806 x B - x Example: Difference of Medians Test Type: sum length, detail Type: return list Example: Difference of Medians Test Example: Difference of Medians Test Example: Difference of Medians Test Type: bootstrap "mymedian" r(diff), reps(1000) The medians are not very different.
    [Show full text]
  • The Cascade Bayesian Approach: Prior Transformation for a Controlled Integration of Internal Data, External Data and Scenarios
    risks Article The Cascade Bayesian Approach: Prior Transformation for a Controlled Integration of Internal Data, External Data and Scenarios Bertrand K. Hassani 1,2,3,* and Alexis Renaudin 4 1 University College London Computer Science, 66-72 Gower Street, London WC1E 6EA, UK 2 LabEx ReFi, Université Paris 1 Panthéon-Sorbonne, CESCES, 106 bd de l’Hôpital, 75013 Paris, France 3 Capegemini Consulting, Tour Europlaza, 92400 Paris-La Défense, France 4 Aon Benfield, The Aon Centre, 122 Leadenhall Street, London EC3V 4AN, UK; [email protected] * Correspondence: [email protected]; Tel.: +44-(0)753-016-7299 Received: 14 March 2018; Accepted: 23 April 2018; Published: 27 April 2018 Abstract: According to the last proposals of the Basel Committee on Banking Supervision, banks or insurance companies under the advanced measurement approach (AMA) must use four different sources of information to assess their operational risk capital requirement. The fourth includes ’business environment and internal control factors’, i.e., qualitative criteria, whereas the three main quantitative sources available to banks for building the loss distribution are internal loss data, external loss data and scenario analysis. This paper proposes an innovative methodology to bring together these three different sources in the loss distribution approach (LDA) framework through a Bayesian strategy. The integration of the different elements is performed in two different steps to ensure an internal data-driven model is obtained. In the first step, scenarios are used to inform the prior distributions and external data inform the likelihood component of the posterior function. In the second step, the initial posterior function is used as the prior distribution and the internal loss data inform the likelihood component of the second posterior function.
    [Show full text]
  • Fundamental Frequency Detection
    Fundamental Frequency Detection Jan Cernock´y,ˇ Valentina Hubeika cernocky|ihubeika @fit.vutbr.cz { } DCGM FIT BUT Brno Fundamental Frequency Detection Jan Cernock´y,ValentinaHubeika,DCGMFITBUTBrnoˇ 1/37 Agenda Fundamental frequency characteristics. • Issues. • Autocorrelation method, AMDF, NFFC. • Formant impact reduction. • Long time predictor. • Cepstrum. • Improvements in fundamental frequency detection. • Fundamental Frequency Detection Jan Cernock´y,ValentinaHubeika,DCGMFITBUTBrnoˇ 2/37 Recap – speech production and its model Fundamental Frequency Detection Jan Cernock´y,ValentinaHubeika,DCGMFITBUTBrnoˇ 3/37 Introduction Fundamental frequency, pitch, is the frequency vocal cords oscillate on: F . • 0 The period of fundamental frequency, (pitch period) is T = 1 . • 0 F0 The term “lag” denotes the pitch period expressed in samples : L = T Fs, where Fs • 0 is the sampling frequency. Fundamental Frequency Detection Jan Cernock´y,ValentinaHubeika,DCGMFITBUTBrnoˇ 4/37 Fundamental Frequency Utilization speech synthesis – melody generation. • coding • – in simple encoding such as LPC, reduction of the bit-stream can be reached by separate transfer of the articulatory tract parameters, energy, voiced/unvoiced sound flag and pitch F0. – in more complex encoders (such as RPE-LTP or ACELP in the GSM cell phones) long time predictor LTP is used. LPT is a filter with a “long” impulse response which however contains only few non-zero components. Fundamental Frequency Detection Jan Cernock´y,ValentinaHubeika,DCGMFITBUTBrnoˇ 5/37 Fundamental Frequency Characteristics F takes the values from 50 Hz (males) to 400 Hz (children), with Fs=8000 Hz these • 0 frequencies correspond to the lags L=160 to 20 samples. It can be seen, that with low values F0 approaches the frame length (20 ms, which corresponds to 160 samples).
    [Show full text]
  • Pearson-Fisher Chi-Square Statistic Revisited
    Information 2011 , 2, 528-545; doi:10.3390/info2030528 OPEN ACCESS information ISSN 2078-2489 www.mdpi.com/journal/information Communication Pearson-Fisher Chi-Square Statistic Revisited Sorana D. Bolboac ă 1, Lorentz Jäntschi 2,*, Adriana F. Sestra ş 2,3 , Radu E. Sestra ş 2 and Doru C. Pamfil 2 1 “Iuliu Ha ţieganu” University of Medicine and Pharmacy Cluj-Napoca, 6 Louis Pasteur, Cluj-Napoca 400349, Romania; E-Mail: [email protected] 2 University of Agricultural Sciences and Veterinary Medicine Cluj-Napoca, 3-5 M ănăş tur, Cluj-Napoca 400372, Romania; E-Mails: [email protected] (A.F.S.); [email protected] (R.E.S.); [email protected] (D.C.P.) 3 Fruit Research Station, 3-5 Horticultorilor, Cluj-Napoca 400454, Romania * Author to whom correspondence should be addressed; E-Mail: [email protected]; Tel: +4-0264-401-775; Fax: +4-0264-401-768. Received: 22 July 2011; in revised form: 20 August 2011 / Accepted: 8 September 2011 / Published: 15 September 2011 Abstract: The Chi-Square test (χ2 test) is a family of tests based on a series of assumptions and is frequently used in the statistical analysis of experimental data. The aim of our paper was to present solutions to common problems when applying the Chi-square tests for testing goodness-of-fit, homogeneity and independence. The main characteristics of these three tests are presented along with various problems related to their application. The main problems identified in the application of the goodness-of-fit test were as follows: defining the frequency classes, calculating the X2 statistic, and applying the χ2 test.
    [Show full text]
  • What Is Bayesian Inference? Bayesian Inference Is at the Core of the Bayesian Approach, Which Is an Approach That Allows Us to Represent Uncertainty As a Probability
    Learn to Use Bayesian Inference in SPSS With Data From the National Child Measurement Programme (2016–2017) © 2019 SAGE Publications Ltd. All Rights Reserved. This PDF has been generated from SAGE Research Methods Datasets. SAGE SAGE Research Methods Datasets Part 2019 SAGE Publications, Ltd. All Rights Reserved. 2 Learn to Use Bayesian Inference in SPSS With Data From the National Child Measurement Programme (2016–2017) Student Guide Introduction This example dataset introduces Bayesian Inference. Bayesian statistics (the general name for all Bayesian-related topics, including inference) has become increasingly popular in recent years, due predominantly to the growth of evermore powerful and sophisticated statistical software. However, Bayesian statistics grew from the ideas of an English mathematician, Thomas Bayes, who lived and worked in the first half of the 18th century and have been refined and adapted by statisticians and mathematicians ever since. Despite its longevity, the Bayesian approach did not become mainstream: the Frequentist approach was and remains the dominant means to conduct statistical analysis. However, there is a renewed interest in Bayesian statistics, part prompted by software development and part by a growing critique of the limitations of the null hypothesis significance testing which dominates the Frequentist approach. This renewed interest can be seen in the incorporation of Bayesian analysis into mainstream statistical software, such as, IBM® SPSS® and in many major statistics text books. Bayesian Inference is at the heart of Bayesian statistics and is different from Frequentist approaches due to how it views probability. In the Frequentist approach, probability is the product of the frequency of random events occurring Page 2 of 19 Learn to Use Bayesian Inference in SPSS With Data From the National Child Measurement Programme (2016–2017) SAGE SAGE Research Methods Datasets Part 2019 SAGE Publications, Ltd.
    [Show full text]
  • Basic Econometrics / Statistics Statistical Distributions: Normal, T, Chi-Sq, & F
    Basic Econometrics / Statistics Statistical Distributions: Normal, T, Chi-Sq, & F Course : Basic Econometrics : HC43 / Statistics B.A. Hons Economics, Semester IV/ Semester III Delhi University Course Instructor: Siddharth Rathore Assistant Professor Economics Department, Gargi College Siddharth Rathore guj75845_appC.qxd 4/16/09 12:41 PM Page 461 APPENDIX C SOME IMPORTANT PROBABILITY DISTRIBUTIONS In Appendix B we noted that a random variable (r.v.) can be described by a few characteristics, or moments, of its probability function (PDF or PMF), such as the expected value and variance. This, however, presumes that we know the PDF of that r.v., which is a tall order since there are all kinds of random variables. In practice, however, some random variables occur so frequently that statisticians have determined their PDFs and documented their properties. For our purpose, we will consider only those PDFs that are of direct interest to us. But keep in mind that there are several other PDFs that statisticians have studied which can be found in any standard statistics textbook. In this appendix we will discuss the following four probability distributions: 1. The normal distribution 2. The t distribution 3. The chi-square (␹2 ) distribution 4. The F distribution These probability distributions are important in their own right, but for our purposes they are especially important because they help us to find out the probability distributions of estimators (or statistics), such as the sample mean and sample variance. Recall that estimators are random variables. Equipped with that knowledge, we will be able to draw inferences about their true population values.
    [Show full text]
  • STAT 830 the Basics of Nonparametric Models The
    STAT 830 The basics of nonparametric models The Empirical Distribution Function { EDF The most common interpretation of probability is that the probability of an event is the long run relative frequency of that event when the basic experiment is repeated over and over independently. So, for instance, if X is a random variable then P (X ≤ x) should be the fraction of X values which turn out to be no more than x in a long sequence of trials. In general an empirical probability or expected value is just such a fraction or average computed from the data. To make this precise, suppose we have a sample X1;:::;Xn of iid real valued random variables. Then we make the following definitions: Definition: The empirical distribution function, or EDF, is n 1 X F^ (x) = 1(X ≤ x): n n i i=1 This is a cumulative distribution function. It is an estimate of F , the cdf of the Xs. People also speak of the empirical distribution of the sample: n 1 X P^(A) = 1(X 2 A) n i i=1 ^ This is the probability distribution whose cdf is Fn. ^ Now we consider the qualities of Fn as an estimate, the standard error of the estimate, the estimated standard error, confidence intervals, simultaneous confidence intervals and so on. To begin with we describe the best known summaries of the quality of an estimator: bias, variance, mean squared error and root mean squared error. Bias, variance, MSE and RMSE There are many ways to judge the quality of estimates of a parameter φ; all of them focus on the distribution of the estimation error φ^−φ.
    [Show full text]
  • Approximate Maximum Likelihood Method for Frequency Estimation
    Statistica Sinica 10(2000), 157-171 APPROXIMATE MAXIMUM LIKELIHOOD METHOD FOR FREQUENCY ESTIMATION Dawei Huang Queensland University of Technology Abstract: A frequency can be estimated by few Discrete Fourier Transform (DFT) coefficients, see Rife and Vincent (1970), Quinn (1994, 1997). This approach is computationally efficient. However, the statistical efficiency of the estimator de- pends on the location of the frequency. In this paper, we explain this approach from a point of view of an Approximate Maximum Likelihood (AML) method. Then we enhance the efficiency of this method by using more DFT coefficients. Compared to 30% and 61% efficiency in the worst cases in Quinn (1994) and Quinn (1997), respectively, we show that if 13 or 25 DFT coefficients are used, AML will achieve at least 90% or 95% efficiency for all frequency locations. Key words and phrases: Approximate Maximum Likelihood, discrete Fourier trans- form, efficiency, fast algorithm, frequency estimation, semi-sufficient statistics. 1. Introduction A model that has been discussed widely in Time Series Analysis and Signal Processing is the following: xt = Acos(tω + φ)+ut,t=0,...,T − 1, (1) where 0 <A,0 <ω<π,and {ut} is a stationary sequence satisfying certain conditions to be specified later. The objective is to estimate the frequency ω from the observations {xt}. After obtaining an estimator of the frequency, the amplitude A and the phase φ can be estimated by a standard linear least squares method. Two topics have been of interest in the study of this model: estimation efficiency and computational complexity. Following the idea of Best Asymp- totic Normal estimation (BAN), the efficiency hereafter is measured by the ratio of the Cramer - Rao Bound (CRB) for unbiased estimators over the variance of the asymptotic distribution of the estimator.
    [Show full text]
  • Sketching for M-Estimators: a Unified Approach to Robust Regression
    Sketching for M-Estimators: A Unified Approach to Robust Regression Kenneth L. Clarkson∗ David P. Woodruffy Abstract ing algorithm often results, since a single pass over A We give algorithms for the M-estimators minx kAx − bkG, suffices to compute SA. n×d n n where A 2 R and b 2 R , and kykG for y 2 R is specified An important property of many of these sketching ≥0 P by a cost function G : R 7! R , with kykG ≡ i G(yi). constructions is that S is a subspace embedding, meaning d The M-estimators generalize `p regression, for which G(x) = that for all x 2 R , kSAxk ≈ kAxk. (Here the vector jxjp. We first show that the Huber measure can be computed norm is generally `p for some p.) For the regression up to relative error in O(nnz(A) log n + poly(d(log n)=")) d time, where nnz(A) denotes the number of non-zero entries problem of minimizing kAx − bk with respect to x 2 R , of the matrix A. Huber is arguably the most widely used for inputs A 2 Rn×d and b 2 Rn, a minor extension of M-estimator, enjoying the robustness properties of `1 as well the embedding condition implies S preserves the norm as the smoothness properties of ` . 2 of the residual vector Ax − b, that is kS(Ax − b)k ≈ We next develop algorithms for general M-estimators. kAx − bk, so that a vector x that makes kS(Ax − b)k We analyze the M-sketch, which is a variation of a sketch small will also make kAx − bk small.
    [Show full text]