Distributional Differences Between Human and Computer Play at Chess
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Videos Bearbeiten Im Überblick: Sieben Aktuelle VIDEOSCHNITT Werkzeuge Für Den Videoschnitt
Miller: Texttool-Allrounder Wego: Schicke Wetter-COMMUNITY-EDITIONManjaro i3: Arch-Derivat mit bereitet CSVs optimal auf S. 54 App für die Konsole S. 44 Tiling-Window-Manager S. 48 Frei kopieren und beliebig weiter verteilen ! 03.2016 03.2016 Guter Schnitt für Bild und Ton, eindrucksvolle Effekte, perfektes Mastering VIDEOSCHNITT Videos bearbeiten Im Überblick: Sieben aktuelle VIDEOSCHNITT Werkzeuge für den Videoschnitt unter Linux im Direktvergleich S. 10 • Veracrypt • Wego • Wego • Veracrypt • Pitivi & OpenShot: Einfach wie noch nie – die neue Generation der Videoschnitt-Werkzeuge S. 20 Lightworks: So kitzeln Sie optimale Ergebnisse aus der kostenlosen Free-Version heraus S. 26 Verschlüsselte Daten sicher verstecken S. 64 Glaubhafte Abstreitbarkeit: Wie Sie mit dem Truecrypt-Nachfolger • SQLiteStudio Stellarium Synology RT1900ac Veracrypt wichtige Daten unauffindbar in Hidden Volumes verbergen Stellarium erweitern S. 32 Workshop SQLiteStudio S. 78 Eigene Objekte und Landschaften Die komfortable Datenbankoberfläche ins virtuelle Planetarium einbinden für Alltagsprogramme auf dem Desktop Top-Distris • Anydesk • Miller PyChess • auf zwei Heft-DVDs ANYDESK • MILLER • PYCHESS • STELLARIUM • VERACRYPT • WEGO • • WEGO • VERACRYPT • STELLARIUM • PYCHESS • MILLER • ANYDESK EUR 8,50 EUR 9,35 sfr 17,00 EUR 10,85 EUR 11,05 EUR 11,05 2 DVD-10 03 www.linux-user.de Deutschland Österreich Schweiz Benelux Spanien Italien 4 196067 008502 03 Editorial Old and busted? Jörg Luther Chefredakteur Sehr geehrte Leserinnen und Leser, viele kleinere, innovative Distributionen seit einem Jahrzehnt kommen Desktop- Immer öfter stellen wir uns aber die haben damit erst gar nicht angefangen und Notebook-Systeme nur noch mit Frage, ob es wirklich noch Sinn ergibt, oder sparen es sich schon lange. Open- 64-Bit-CPUs, sodass sich die Zahl der moderne Distributionen überhaupt Suse verzichtet seit Leap 42.1 darauf; das 32-Bit-Systeme in freier Wildbahn lang- noch als 32-Bit-Images beizulegen. -

The 12Th Top Chess Engine Championship
TCEC12: the 12th Top Chess Engine Championship Article Accepted Version Haworth, G. and Hernandez, N. (2019) TCEC12: the 12th Top Chess Engine Championship. ICGA Journal, 41 (1). pp. 24-30. ISSN 1389-6911 doi: https://doi.org/10.3233/ICG-190090 Available at http://centaur.reading.ac.uk/76985/ It is advisable to refer to the publisher’s version if you intend to cite from the work. See Guidance on citing . To link to this article DOI: http://dx.doi.org/10.3233/ICG-190090 Publisher: The International Computer Games Association All outputs in CentAUR are protected by Intellectual Property Rights law, including copyright law. Copyright and IPR is retained by the creators or other copyright holders. Terms and conditions for use of this material are defined in the End User Agreement . www.reading.ac.uk/centaur CentAUR Central Archive at the University of Reading Reading’s research outputs online TCEC12: the 12th Top Chess Engine Championship Guy Haworth and Nelson Hernandez1 Reading, UK and Maryland, USA After the successes of TCEC Season 11 (Haworth and Hernandez, 2018a; TCEC, 2018), the Top Chess Engine Championship moved straight on to Season 12, starting April 18th 2018 with the same divisional structure if somewhat evolved. Five divisions, each of eight engines, played two or more ‘DRR’ double round robin phases each, with promotions and relegations following. Classic tempi gradually lengthened and the Premier division’s top two engines played a 100-game match to determine the Grand Champion. The strategy for the selection of mandated openings was finessed from division to division. -

Development of Games for Users with Visual Impairment Czech Technical University in Prague Faculty of Electrical Engineering
Development of games for users with visual impairment Czech Technical University in Prague Faculty of Electrical Engineering Dina Chernova January 2017 Acknowledgement I would first like to thank Bc. Honza Had´aˇcekfor his valuable advice. I am also very grateful to my supervisor Ing. Daniel Nov´ak,Ph.D. and to all participants that were involved in testing of my application for their precious time. I must express my profound gratitude to my loved ones for their support and continuous encouragement throughout my years of study. This accomplishment would not have been possible without them. Thank you. 5 Declaration I declare that I have developed this thesis on my own and that I have stated all the information sources in accordance with the methodological guideline of adhering to ethical principles during the preparation of university theses. In Prague 09.01.2017 Author 6 Abstract This bachelor thesis deals with analysis and implementation of mobile application that allows visually impaired people to play chess on their smart phones. The application con- trol is performed using special gestures and text{to{speech engine as a sound accompanier. For human against computer game mode I have used currently the best game engine called Stockfish. The application is developed under Android mobile platform. Keywords: chess; visually impaired; Android; Bakal´aˇrsk´apr´acese zab´yv´aanal´yzoua implementac´ımobiln´ıaplikace, kter´aumoˇzˇnuje zrakovˇepostiˇzen´ymlidem hr´atˇsachy na sv´emsmartphonu. Ovl´ad´an´ıaplikace se prov´ad´ı pomoc´ıspeci´aln´ıch gest a text{to{speech enginu pro zvukov´edoprov´azen´ı.V reˇzimu ˇclovˇek versus poˇc´ıtaˇcjsem pouˇzilasouˇcasnˇenejlepˇs´ıhern´ıengine Stockfish. -

Game Changer
Matthew Sadler and Natasha Regan Game Changer AlphaZero’s Groundbreaking Chess Strategies and the Promise of AI New In Chess 2019 Contents Explanation of symbols 6 Foreword by Garry Kasparov �������������������������������������������������������������������������������� 7 Introduction by Demis Hassabis 11 Preface 16 Introduction ������������������������������������������������������������������������������������������������������������ 19 Part I AlphaZero’s history . 23 Chapter 1 A quick tour of computer chess competition 24 Chapter 2 ZeroZeroZero ������������������������������������������������������������������������������ 33 Chapter 3 Demis Hassabis, DeepMind and AI 54 Part II Inside the box . 67 Chapter 4 How AlphaZero thinks 68 Chapter 5 AlphaZero’s style – meeting in the middle 87 Part III Themes in AlphaZero’s play . 131 Chapter 6 Introduction to our selected AlphaZero themes 132 Chapter 7 Piece mobility: outposts 137 Chapter 8 Piece mobility: activity 168 Chapter 9 Attacking the king: the march of the rook’s pawn 208 Chapter 10 Attacking the king: colour complexes 235 Chapter 11 Attacking the king: sacrifices for time, space and damage 276 Chapter 12 Attacking the king: opposite-side castling 299 Chapter 13 Attacking the king: defence 321 Part IV AlphaZero’s -

A New Look at the Tayler by David Kane
A New Look at the Tayler by David kane I: Introduction The Tayler Variation (aka the Tayler Opening) is a line that has been unjustly neglected, in my view. The line is of surprisingly recent vintage though it is often confused with the Inverted Hungarian (or Inverted Hanham Defense), a line which shares the same opening moves: 1. e4 e5 2. Nf3 Nc6 3. Be2: The Inverted Hungarian is an old opening, dating back to the 1860ʼs, at least. Tartakower played it a few times in the 1920ʼs with mixed results, using the continuation, 3...Nf6 4. d3: a rather unenterprising setup for White. In 1981 British player, John Tayler (see biographical note), published an article in the British publication Chess (vol. 46) on a line he had developed stemming from the sharp 4. d4!?. This is a move which apparently no one had thought to play before, and one that transforms the sedate Inverted Hungarian into something else altogether. Technically, it is really the Tayler Variation to the Inverted Hungarian Defense rather than the Tayler Opening, though through usage, the terms are interchangeable for all practical purposes. As has been so often the case when it comes to unorthodox lines, I first heard of this opening via Mike Basman when he published a cassette on it back in the early 80ʼs (still available through audiochess.com). Tayler 2 The line stirred some interest at the time but gradually seems to have been forgotten. The final nail in the coffin was probably some light analysis published by Eric Schiller in Gambit Chess Openings (and elsewhere) where he dismisses the line primarily due to his loss in the game Schiller-Martinovsky, Chicago 1986. -

(2021), 2814-2819 Research Article Can Chess Ever Be Solved Na
Turkish Journal of Computer and Mathematics Education Vol.12 No.2 (2021), 2814-2819 Research Article Can Chess Ever Be Solved Naveen Kumar1, Bhayaa Sharma2 1,2Department of Mathematics, University Institute of Sciences, Chandigarh University, Gharuan, Mohali, Punjab-140413, India [email protected], [email protected] Article History: Received: 11 January 2021; Accepted: 27 February 2021; Published online: 5 April 2021 Abstract: Data Science and Artificial Intelligence have been all over the world lately,in almost every possible field be it finance,education,entertainment,healthcare,astronomy, astrology, and many more sports is no exception. With so much data, statistics, and analysis available in this particular field, when everything is being recorded it has become easier for team selectors, broadcasters, audience, sponsors, most importantly for players themselves to prepare against various opponents. Even the analysis has improved over the period of time with the evolvement of AI, not only analysis one can even predict the things with the insights available. This is not even restricted to this,nowadays players are trained in such a manner that they are capable of taking the most feasible and rational decisions in any given situation. Chess is one of those sports that depend on calculations, algorithms, analysis, decisions etc. Being said that whenever the analysis is involved, we have always improvised on the techniques. Algorithms are somethingwhich can be solved with the help of various software, does that imply that chess can be fully solved,in simple words does that mean that if both the players play the best moves respectively then the game must end in a draw or does that mean that white wins having the first move advantage. -
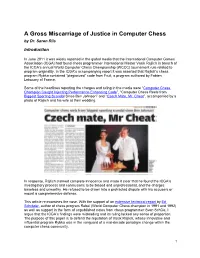
Draft – Not for Circulation
A Gross Miscarriage of Justice in Computer Chess by Dr. Søren Riis Introduction In June 2011 it was widely reported in the global media that the International Computer Games Association (ICGA) had found chess programmer International Master Vasik Rajlich in breach of the ICGA‟s annual World Computer Chess Championship (WCCC) tournament rule related to program originality. In the ICGA‟s accompanying report it was asserted that Rajlich‟s chess program Rybka contained “plagiarized” code from Fruit, a program authored by Fabien Letouzey of France. Some of the headlines reporting the charges and ruling in the media were “Computer Chess Champion Caught Injecting Performance-Enhancing Code”, “Computer Chess Reels from Biggest Sporting Scandal Since Ben Johnson” and “Czech Mate, Mr. Cheat”, accompanied by a photo of Rajlich and his wife at their wedding. In response, Rajlich claimed complete innocence and made it clear that he found the ICGA‟s investigatory process and conclusions to be biased and unprofessional, and the charges baseless and unworthy. He refused to be drawn into a protracted dispute with his accusers or mount a comprehensive defense. This article re-examines the case. With the support of an extensive technical report by Ed Schröder, author of chess program Rebel (World Computer Chess champion in 1991 and 1992) as well as support in the form of unpublished notes from chess programmer Sven Schüle, I argue that the ICGA‟s findings were misleading and its ruling lacked any sense of proportion. The purpose of this paper is to defend the reputation of Vasik Rajlich, whose innovative and influential program Rybka was in the vanguard of a mid-decade paradigm change within the computer chess community. -
Download Source Engine for Pc Free Download Source Engine for Pc Free
download source engine for pc free Download source engine for pc free. Completing the CAPTCHA proves you are a human and gives you temporary access to the web property. What can I do to prevent this in the future? If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware. If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices. Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store. Cloudflare Ray ID: 67a0b2f3bed7f14e • Your IP : 188.246.226.140 • Performance & security by Cloudflare. Download source engine for pc free. Completing the CAPTCHA proves you are a human and gives you temporary access to the web property. What can I do to prevent this in the future? If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware. If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices. Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store. Cloudflare Ray ID: 67a0b2f3c99315dc • Your IP : 188.246.226.140 • Performance & security by Cloudflare. -

The SSDF Chess Engine Rating List, 2019-02
The SSDF Chess Engine Rating List, 2019-02 Article Accepted Version The SSDF report Sandin, L. and Haworth, G. (2019) The SSDF Chess Engine Rating List, 2019-02. ICGA Journal, 41 (2). 113. ISSN 1389- 6911 doi: https://doi.org/10.3233/ICG-190107 Available at http://centaur.reading.ac.uk/82675/ It is advisable to refer to the publisher’s version if you intend to cite from the work. See Guidance on citing . Published version at: https://doi.org/10.3233/ICG-190085 To link to this article DOI: http://dx.doi.org/10.3233/ICG-190107 Publisher: The International Computer Games Association All outputs in CentAUR are protected by Intellectual Property Rights law, including copyright law. Copyright and IPR is retained by the creators or other copyright holders. Terms and conditions for use of this material are defined in the End User Agreement . www.reading.ac.uk/centaur CentAUR Central Archive at the University of Reading Reading’s research outputs online THE SSDF RATING LIST 2019-02-28 148673 games played by 377 computers Rating + - Games Won Oppo ------ --- --- ----- --- ---- 1 Stockfish 9 x64 1800X 3.6 GHz 3494 32 -30 642 74% 3308 2 Komodo 12.3 x64 1800X 3.6 GHz 3456 30 -28 640 68% 3321 3 Stockfish 9 x64 Q6600 2.4 GHz 3446 50 -48 200 57% 3396 4 Stockfish 8 x64 1800X 3.6 GHz 3432 26 -24 1059 77% 3217 5 Stockfish 8 x64 Q6600 2.4 GHz 3418 38 -35 440 72% 3251 6 Komodo 11.01 x64 1800X 3.6 GHz 3397 23 -22 1134 72% 3229 7 Deep Shredder 13 x64 1800X 3.6 GHz 3360 25 -24 830 66% 3246 8 Booot 6.3.1 x64 1800X 3.6 GHz 3352 29 -29 560 54% 3319 9 Komodo 9.1 -

March 2020 Uschess.Org the United States’ Largest Chess Specialty Retailer
March 2020 USChess.org The United States’ Largest Chess Specialty Retailer 888.51.CHESS (512.4377) www.USCFSales.com ƩĂĐŬŝŶŐǁŝƚŚŐϮͲŐϰ The 100 Endgames You Must Know Workbook The Modern Way to Get the Upper Hand in Chess WƌĂĐƟĐĂůŶĚŐĂŵĞƐdžĞƌĐŝƐĞƐĨŽƌǀĞƌLJŚĞƐƐWůĂLJĞƌ Dmitry Kryavkin 288 pages - $24.95 Jesus de la Villa 288 pages - $24.95 dŚĞƉĂǁŶƚŚƌƵƐƚŐϮͲŐϰŝƐĂƉĞƌĨĞĐƚǁĂLJƚŽĐŽŶĨƵƐĞLJŽƵƌ ͞/ůŽǀĞƚŚŝƐŬ͊/ŶŽƌĚĞƌƚŽŵĂƐƚĞƌĞŶĚŐĂŵĞƉƌŝŶĐŝƉůĞƐLJŽƵ ŽƉƉŽŶĞŶƚƐĂŶĚĚŝƐƌƵƉƚƚŚĞŝƌƉŽƐŝƟŽŶ͘tŝƚŚůŽƚƐŽĨŝŶƐƚƌƵĐƟǀĞ ǁŝůůŶĞĞĚƚŽƉƌĂĐƟĐĞƚŚĞŵ͘͟ʹNM Han Schut, Chess.com ĞdžĂŵƉůĞƐ'D<ƌLJĂŬǀŝŶƐŚŽǁƐŚŽǁŝƚĐĂŶďĞƵƐĞĚƚŽĚĞĨĞĂƚ ͞dŚĞƉĞƌĨĞĐƚƐƵƉƉůĞŵĞŶƚƚŽĞůĂsŝůůĂ͛ƐŵĂŶƵĂů͘dŽŐĂŝŶ ůĂĐŬŝŶƚŚĞƵƚĐŚ͕ƚŚĞYƵĞĞŶ͛Ɛ'Ăŵďŝƚ͕ƚŚĞEŝŵnjŽͲ/ŶĚŝĂŶ͕ ƐƵĸĐŝĞŶƚŬŶŽǁůĞĚŐĞŽĨƚŚĞŽƌĞƟĐĂůĞŶĚŐĂŵĞƐLJŽƵƌĞĂůůLJŽŶůLJ ƚŚĞ<ŝŶŐ͛Ɛ/ŶĚŝĂŶ͕ƚŚĞ^ůĂǀĂŶĚƚŚĞŶŐůŝƐŚKƉĞŶŝŶŐ͘>ĞĂƌŶ ŶĞĞĚƚǁŽďŽŽŬƐ͘͟ʹIM Herman Grooten, Schaaksite NEW! ƚŚĞƚLJƉŝĐĂůǁĂLJƐƚŽŐĂŝŶƚĞŵƉŝ͕ŬĞĞƉƚŚĞŵŽŵĞŶƚƵŵĂŶĚ ŵĂdžŝŵŝnjĞLJŽƵƌŽƉƉŽŶĞŶƚ͛ƐƉƌŽďůĞŵƐ͘ Strategic Chess Exercises Keep It Simple 1.d4 Find the Right Way to Outplay Your Opponent ^ŽůŝĚĂŶĚ^ƚƌĂŝŐŚƞŽƌǁĂƌĚŚĞƐƐKƉĞŶŝŶŐZĞƉĞƌƚŽŝƌĞĨŽƌtŚŝƚĞ Emmanuel Bricard 224 pages - $24.95 Christof Sielecki 432 pages - $29.95 &ŝŶĂůůLJĂŶĞdžĞƌĐŝƐĞƐŬƚŚĂƚŝƐŶŽƚĂďŽƵƚƚĂĐƟĐƐ͊ ^ŝĞůĞĐŬŝ͛ƐƌĞƉĞƌƚŽŝƌĞǁŝƚŚϭ͘ĚϰŵĂLJďĞĞǀĞŶĞĂƐŝĞƌƚŽ ͞ƌŝĐĂƌĚŝƐĐůĞĂƌůLJĂǀĞƌLJŐŝŌĞĚƚƌĂŝŶĞƌ͘,ĞƐĞůĞĐƚĞĚĂƐƵƉĞƌď ŵĂƐƚĞƌƚŚĂŶŚŝƐϭ͘ĞϰƌĞĐŽŵŵĞŶĚĂƟŽŶƐ͕ďĞĐĂƵƐĞŝƚŝƐƐƵĐŚĂ ƌĂŶŐĞŽĨƉŽƐŝƟŽŶƐĂŶĚĞdžƉůĂŝŶƐƚŚĞƐŽůƵƟŽŶƐĞdžƚƌĞŵĞůLJ ĐŽŚĞƌĞŶƚƐLJƐƚĞŵ͗ƚŚĞŵĂŝŶĐŽŶĐĞƉƚŝƐĨŽƌtŚŝƚĞƚŽƉůĂLJϭ͘Ěϰ͕ ǁĞůů͘͟ʹGM Daniel King Ϯ͘EĨϯ͕ϯ͘Őϯ͕ϰ͘ŐϮ͕ϱ͘ϬͲϬĂŶĚŝŶŵŽƐƚĐĂƐĞƐϲ͘Đϰ͘ ͞&ŽƌĐŚĞƐƐĐŽĂĐŚĞƐƚŚŝƐŬŝƐŶŽƚŚŝŶŐƐŚŽƌƚŽĨƉŚĞŶŽŵĞŶĂů͘͟ ͞Ɛ/ƚŚŝŶŬƚŚĂƚ/ƐŚŽƵůĚŬĞĞƉŵLJĂĚǀŝĐĞ͚ƐŝŵƉůĞ͕͛/ǁŽƵůĚƐĂLJ -

The TCEC20 Computer Chess Superfinal: a Perspective
The TCEC20 Computer Chess Superfinal: a Perspective GM Matthew Sadler1 London, UK 1 THE TCEC20 PREMIER DIVISION Just like last year, Season 20 DivP gathered a host of familiar faces and once again, one of those faces had a facelift! The venerable KOMODO engine had been given an NNUE beauty boost and there was a feeling that KOMODO DRAGON might prove a threat to LEELA’s and STOCKFISH’s customary tickets to the Superfinal. There was also an updated STOOFVLEES to enjoy while ETHEREAL came storming back to DivP after a convincing victory in League 1. ROFCHADE just pipped NNUE-powered IGEL on tie- break for the second DivP spot. In the end, KOMODO turned out to have indeed received a significant boost from NNUE, pipping ALLIESTEIN for third place. However, both LEELA and STOCKFISH seemed to have made another quantum leap forwards, dominating the field and ending joint first on 38/56, 5.5 points clear of KOMODO DRAGON! Both LEELA and STOCKFISH scored an astonishing 24 wins, with LEELA winning 24 of its 28 White games and STOCKFISH 22! Both winners lost 4 games, all as Black, with LEELA notably tripping up against bottom-marker ROFCHADE and STOCKFISH being beautifully squeezed by STOOFVLEES. The high winning percentage this time is explained by the new high-bias opening book designed for the Premier Division. I had slightly mixed feelings about it as LEELA and STOCKFISH winning virtually all their White games felt like going a bit too much the other way: you want them to have to work a bit harder for their Superfinal places! However, it was once again a very entertaining tournament with plenty of good games. -

The TCEC Cup 2 Report
TCEC Cup 2 Article Accepted Version The TCEC Cup 2 report Haworth, G. and Hernandez, N. (2019) TCEC Cup 2. ICGA Journal, 41 (2). pp. 100-107. ISSN 1389-6911 doi: https://doi.org/10.3233/ICG-190104 Available at http://centaur.reading.ac.uk/81390/ It is advisable to refer to the publisher’s version if you intend to cite from the work. See Guidance on citing . Published version at: https://content.iospress.com/articles/icga-journal/icg190104 To link to this article DOI: http://dx.doi.org/10.3233/ICG-190104 Publisher: The International Computer Games Association All outputs in CentAUR are protected by Intellectual Property Rights law, including copyright law. Copyright and IPR is retained by the creators or other copyright holders. Terms and conditions for use of this material are defined in the End User Agreement . www.reading.ac.uk/centaur CentAUR Central Archive at the University of Reading Reading’s research outputs online TCEC Cup 2 Guy Haworth and Nelson Hernandez1 Reading, UK and Maryland, USA The knockout format of TCEC Cup 1 (Haworth and Hernandez, 2019a/b) was well received by its audience and was adopted as a regular interlude between the TCEC Seasons’ Division P and Superfinal. TCEC Cup 2 was nested within TCEC14 (Haworth and Hernandez, 2019c/d) and began on January 17th 2019 with 32 chess engines and only a few minor changes from the inaugural Cup event. The ‘standard pairing’ was again used, with seed s playing seed 26-r-s+1 in round r if the wins all go to the higher seed.