Analytic and Algebraic Geometry Common Problems, Different Methods
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Analytic Geometry
Guide Study Georgia End-Of-Course Tests Georgia ANALYTIC GEOMETRY TABLE OF CONTENTS INTRODUCTION ...........................................................................................................5 HOW TO USE THE STUDY GUIDE ................................................................................6 OVERVIEW OF THE EOCT .........................................................................................8 PREPARING FOR THE EOCT ......................................................................................9 Study Skills ........................................................................................................9 Time Management .....................................................................................10 Organization ...............................................................................................10 Active Participation ...................................................................................11 Test-Taking Strategies .....................................................................................11 Suggested Strategies to Prepare for the EOCT ..........................................12 Suggested Strategies the Day before the EOCT ........................................13 Suggested Strategies the Morning of the EOCT ........................................13 Top 10 Suggested Strategies during the EOCT .........................................14 TEST CONTENT ........................................................................................................15 -

Chapter 11. Three Dimensional Analytic Geometry and Vectors
Chapter 11. Three dimensional analytic geometry and vectors. Section 11.5 Quadric surfaces. Curves in R2 : x2 y2 ellipse + =1 a2 b2 x2 y2 hyperbola − =1 a2 b2 parabola y = ax2 or x = by2 A quadric surface is the graph of a second degree equation in three variables. The most general such equation is Ax2 + By2 + Cz2 + Dxy + Exz + F yz + Gx + Hy + Iz + J =0, where A, B, C, ..., J are constants. By translation and rotation the equation can be brought into one of two standard forms Ax2 + By2 + Cz2 + J =0 or Ax2 + By2 + Iz =0 In order to sketch the graph of a quadric surface, it is useful to determine the curves of intersection of the surface with planes parallel to the coordinate planes. These curves are called traces of the surface. Ellipsoids The quadric surface with equation x2 y2 z2 + + =1 a2 b2 c2 is called an ellipsoid because all of its traces are ellipses. 2 1 x y 3 2 1 z ±1 ±2 ±3 ±1 ±2 The six intercepts of the ellipsoid are (±a, 0, 0), (0, ±b, 0), and (0, 0, ±c) and the ellipsoid lies in the box |x| ≤ a, |y| ≤ b, |z| ≤ c Since the ellipsoid involves only even powers of x, y, and z, the ellipsoid is symmetric with respect to each coordinate plane. Example 1. Find the traces of the surface 4x2 +9y2 + 36z2 = 36 1 in the planes x = k, y = k, and z = k. Identify the surface and sketch it. Hyperboloids Hyperboloid of one sheet. The quadric surface with equations x2 y2 z2 1. -
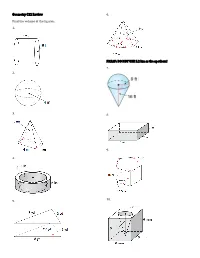
Geometry C12 Review Find the Volume of the Figures. 1. 2. 3. 4. 5. 6
Geometry C12 Review 6. Find the volume of the figures. 1. PREAP: DO NOT USE 5.2 km as the apothem! 7. 2. 3. 8. 9. 4. 10. 5. 11. 16. 17. 12. 18. 13. 14. 19. 15. 20. 21. A sphere has a volume of 7776π in3. What is the radius 33. Two prisms are similar. The ratio of their volumes is of the sphere? 8:27. The surface area of the smaller prism is 72 in2. Find the surface area of the larger prism. 22a. A sphere has a volume of 36π cm3. What is the radius and diameter of the sphere? 22b. A sphere has a volume of 45 ft3. What is the 34. The prisms are similar. approximate radius of the sphere? a. What is the scale factor? 23. The scale factor (ratio of sides) of two similar solids is b. What is the ratio of surface 3:7. What are the ratios of their surface areas and area? volumes? c. What is the ratio of volume? d. Find the volume of the 24. The scale factor of two similar solids is 12:5. What are smaller prism. the ratios of their surface areas and volumes? 35. The prisms are similar. 25. The scale factor of two similar solids is 6:11. What are a. What is the scale factor? the ratios of their surface areas and volumes? b. What is the ratio of surface area? 26. The ratio of the volumes of two similar solids is c. What is the ratio of 343:2197. What is the scale factor (ratio of sides)? volume? d. -

Algebraic Geometry Michael Stoll
Introductory Geometry Course No. 100 351 Fall 2005 Second Part: Algebraic Geometry Michael Stoll Contents 1. What Is Algebraic Geometry? 2 2. Affine Spaces and Algebraic Sets 3 3. Projective Spaces and Algebraic Sets 6 4. Projective Closure and Affine Patches 9 5. Morphisms and Rational Maps 11 6. Curves — Local Properties 14 7. B´ezout’sTheorem 18 2 1. What Is Algebraic Geometry? Linear Algebra can be seen (in parts at least) as the study of systems of linear equations. In geometric terms, this can be interpreted as the study of linear (or affine) subspaces of Cn (say). Algebraic Geometry generalizes this in a natural way be looking at systems of polynomial equations. Their geometric realizations (their solution sets in Cn, say) are called algebraic varieties. Many questions one can study in various parts of mathematics lead in a natural way to (systems of) polynomial equations, to which the methods of Algebraic Geometry can be applied. Algebraic Geometry provides a translation between algebra (solutions of equations) and geometry (points on algebraic varieties). The methods are mostly algebraic, but the geometry provides the intuition. Compared to Differential Geometry, in Algebraic Geometry we consider a rather restricted class of “manifolds” — those given by polynomial equations (we can allow “singularities”, however). For example, y = cos x defines a perfectly nice differentiable curve in the plane, but not an algebraic curve. In return, we can get stronger results, for example a criterion for the existence of solutions (in the complex numbers), or statements on the number of solutions (for example when intersecting two curves), or classification results. -

ANALYTIC GEOMETRY Revision Log
Guide Study Georgia End-Of-Course Tests Georgia ANALYTIC GEOMETRYJanuary 2014 Revision Log August 2013: Unit 7 (Applications of Probability) page 200; Key Idea #7 – text and equation were updated to denote intersection rather than union page 203; Review Example #2 Solution – union symbol has been corrected to intersection symbol in lines 3 and 4 of the solution text January 2014: Unit 1 (Similarity, Congruence, and Proofs) page 33; Review Example #2 – “Segment Addition Property” has been updated to “Segment Addition Postulate” in step 13 of the solution page 46; Practice Item #2 – text has been specified to indicate that point V lies on segment SU page 59; Practice Item #1 – art has been updated to show points on YX and YZ Unit 3 (Circles and Volume) page 74; Key Idea #17 – the reference to Key Idea #15 has been updated to Key Idea #16 page 84; Key Idea #3 – the degree symbol (°) has been removed from 360, and central angle is noted by θ instead of x in the formula and the graphic page 84; Important Tip – the word “formulas” has been corrected to “formula”, and x has been replaced by θ in the formula for arc length page 85; Key Idea #4 – the degree symbol (°) has been added to the conversion factor page 85; Key Idea #5 – text has been specified to indicate a central angle, and central angle is noted by θ instead of x page 85; Key Idea #6 – the degree symbol (°) has been removed from 360, and central angle is noted by θ instead of x in the formula and the graphic page 87; Solution Step i – the degree symbol (°) has been added to the conversion -

Analytic Geometry
STATISTIC ANALYTIC GEOMETRY SESSION 3 STATISTIC SESSION 3 Session 3 Analytic Geometry Geometry is all about shapes and their properties. If you like playing with objects, or like drawing, then geometry is for you! Geometry can be divided into: Plane Geometry is about flat shapes like lines, circles and triangles ... shapes that can be drawn on a piece of paper Solid Geometry is about three dimensional objects like cubes, prisms, cylinders and spheres Point, Line, Plane and Solid A Point has no dimensions, only position A Line is one-dimensional A Plane is two dimensional (2D) A Solid is three-dimensional (3D) Plane Geometry Plane Geometry is all about shapes on a flat surface (like on an endless piece of paper). 2D Shapes Activity: Sorting Shapes Triangles Right Angled Triangles Interactive Triangles Quadrilaterals (Rhombus, Parallelogram, etc) Rectangle, Rhombus, Square, Parallelogram, Trapezoid and Kite Interactive Quadrilaterals Shapes Freeplay Perimeter Area Area of Plane Shapes Area Calculation Tool Area of Polygon by Drawing Activity: Garden Area General Drawing Tool Polygons A Polygon is a 2-dimensional shape made of straight lines. Triangles and Rectangles are polygons. Here are some more: Pentagon Pentagra m Hexagon Properties of Regular Polygons Diagonals of Polygons Interactive Polygons The Circle Circle Pi Circle Sector and Segment Circle Area by Sectors Annulus Activity: Dropping a Coin onto a Grid Circle Theorems (Advanced Topic) Symbols There are many special symbols used in Geometry. Here is a short reference for you: -

Multidisciplinary Design Project Engineering Dictionary Version 0.0.2
Multidisciplinary Design Project Engineering Dictionary Version 0.0.2 February 15, 2006 . DRAFT Cambridge-MIT Institute Multidisciplinary Design Project This Dictionary/Glossary of Engineering terms has been compiled to compliment the work developed as part of the Multi-disciplinary Design Project (MDP), which is a programme to develop teaching material and kits to aid the running of mechtronics projects in Universities and Schools. The project is being carried out with support from the Cambridge-MIT Institute undergraduate teaching programe. For more information about the project please visit the MDP website at http://www-mdp.eng.cam.ac.uk or contact Dr. Peter Long Prof. Alex Slocum Cambridge University Engineering Department Massachusetts Institute of Technology Trumpington Street, 77 Massachusetts Ave. Cambridge. Cambridge MA 02139-4307 CB2 1PZ. USA e-mail: [email protected] e-mail: [email protected] tel: +44 (0) 1223 332779 tel: +1 617 253 0012 For information about the CMI initiative please see Cambridge-MIT Institute website :- http://www.cambridge-mit.org CMI CMI, University of Cambridge Massachusetts Institute of Technology 10 Miller’s Yard, 77 Massachusetts Ave. Mill Lane, Cambridge MA 02139-4307 Cambridge. CB2 1RQ. USA tel: +44 (0) 1223 327207 tel. +1 617 253 7732 fax: +44 (0) 1223 765891 fax. +1 617 258 8539 . DRAFT 2 CMI-MDP Programme 1 Introduction This dictionary/glossary has not been developed as a definative work but as a useful reference book for engi- neering students to search when looking for the meaning of a word/phrase. It has been compiled from a number of existing glossaries together with a number of local additions. -

Topics in Complex Analytic Geometry
version: February 24, 2012 (revised and corrected) Topics in Complex Analytic Geometry by Janusz Adamus Lecture Notes PART II Department of Mathematics The University of Western Ontario c Copyright by Janusz Adamus (2007-2012) 2 Janusz Adamus Contents 1 Analytic tensor product and fibre product of analytic spaces 5 2 Rank and fibre dimension of analytic mappings 8 3 Vertical components and effective openness criterion 17 4 Flatness in complex analytic geometry 24 5 Auslander-type effective flatness criterion 31 This document was typeset using AMS-LATEX. Topics in Complex Analytic Geometry - Math 9607/9608 3 References [I] J. Adamus, Complex analytic geometry, Lecture notes Part I (2008). [A1] J. Adamus, Natural bound in Kwieci´nski'scriterion for flatness, Proc. Amer. Math. Soc. 130, No.11 (2002), 3165{3170. [A2] J. Adamus, Vertical components in fibre powers of analytic spaces, J. Algebra 272 (2004), no. 1, 394{403. [A3] J. Adamus, Vertical components and flatness of Nash mappings, J. Pure Appl. Algebra 193 (2004), 1{9. [A4] J. Adamus, Flatness testing and torsion freeness of analytic tensor powers, J. Algebra 289 (2005), no. 1, 148{160. [ABM1] J. Adamus, E. Bierstone, P. D. Milman, Uniform linear bound in Chevalley's lemma, Canad. J. Math. 60 (2008), no.4, 721{733. [ABM2] J. Adamus, E. Bierstone, P. D. Milman, Geometric Auslander criterion for flatness, to appear in Amer. J. Math. [ABM3] J. Adamus, E. Bierstone, P. D. Milman, Geometric Auslander criterion for openness of an algebraic morphism, preprint (arXiv:1006.1872v1). [Au] M. Auslander, Modules over unramified regular local rings, Illinois J. -

Phylogenetic Algebraic Geometry
PHYLOGENETIC ALGEBRAIC GEOMETRY NICHOLAS ERIKSSON, KRISTIAN RANESTAD, BERND STURMFELS, AND SETH SULLIVANT Abstract. Phylogenetic algebraic geometry is concerned with certain complex projec- tive algebraic varieties derived from finite trees. Real positive points on these varieties represent probabilistic models of evolution. For small trees, we recover classical geometric objects, such as toric and determinantal varieties and their secant varieties, but larger trees lead to new and largely unexplored territory. This paper gives a self-contained introduction to this subject and offers numerous open problems for algebraic geometers. 1. Introduction Our title is meant as a reference to the existing branch of mathematical biology which is known as phylogenetic combinatorics. By “phylogenetic algebraic geometry” we mean the study of algebraic varieties which represent statistical models of evolution. For general background reading on phylogenetics we recommend the books by Felsenstein [11] and Semple-Steel [21]. They provide an excellent introduction to evolutionary trees, from the perspectives of biology, computer science, statistics and mathematics. They also offer numerous references to relevant papers, in addition to the more recent ones listed below. Phylogenetic algebraic geometry furnishes a rich source of interesting varieties, includ- ing familiar ones such as toric varieties, secant varieties and determinantal varieties. But these are very special cases, and one quickly encounters a cornucopia of new varieties. The objective of this paper is to give an introduction to this subject area, aimed at students and researchers in algebraic geometry, and to suggest some concrete research problems. The basic object in a phylogenetic model is a tree T which is rooted and has n labeled leaves. -

Chapter 1: Analytic Geometry
1 Analytic Geometry Much of the mathematics in this chapter will be review for you. However, the examples will be oriented toward applications and so will take some thought. In the (x,y) coordinate system we normally write the x-axis horizontally, with positive numbers to the right of the origin, and the y-axis vertically, with positive numbers above the origin. That is, unless stated otherwise, we take “rightward” to be the positive x- direction and “upward” to be the positive y-direction. In a purely mathematical situation, we normally choose the same scale for the x- and y-axes. For example, the line joining the origin to the point (a,a) makes an angle of 45◦ with the x-axis (and also with the y-axis). In applications, often letters other than x and y are used, and often different scales are chosen in the horizontal and vertical directions. For example, suppose you drop something from a window, and you want to study how its height above the ground changes from second to second. It is natural to let the letter t denote the time (the number of seconds since the object was released) and to let the letter h denote the height. For each t (say, at one-second intervals) you have a corresponding height h. This information can be tabulated, and then plotted on the (t, h) coordinate plane, as shown in figure 1.0.1. We use the word “quadrant” for each of the four regions into which the plane is divided by the axes: the first quadrant is where points have both coordinates positive, or the “northeast” portion of the plot, and the second, third, and fourth quadrants are counted off counterclockwise, so the second quadrant is the northwest, the third is the southwest, and the fourth is the southeast. -

Hydraulics Manual Glossary G - 3
Glossary G - 1 GLOSSARY OF HIGHWAY-RELATED DRAINAGE TERMS (Reprinted from the 1999 edition of the American Association of State Highway and Transportation Officials Model Drainage Manual) G.1 Introduction This Glossary is divided into three parts: · Introduction, · Glossary, and · References. It is not intended that all the terms in this Glossary be rigorously accurate or complete. Realistically, this is impossible. Depending on the circumstance, a particular term may have several meanings; this can never change. The primary purpose of this Glossary is to define the terms found in the Highway Drainage Guidelines and Model Drainage Manual in a manner that makes them easier to interpret and understand. A lesser purpose is to provide a compendium of terms that will be useful for both the novice as well as the more experienced hydraulics engineer. This Glossary may also help those who are unfamiliar with highway drainage design to become more understanding and appreciative of this complex science as well as facilitate communication between the highway hydraulics engineer and others. Where readily available, the source of a definition has been referenced. For clarity or format purposes, cited definitions may have some additional verbiage contained in double brackets [ ]. Conversely, three “dots” (...) are used to indicate where some parts of a cited definition were eliminated. Also, as might be expected, different sources were found to use different hyphenation and terminology practices for the same words. Insignificant changes in this regard were made to some cited references and elsewhere to gain uniformity for the terms contained in this Glossary: as an example, “groundwater” vice “ground-water” or “ground water,” and “cross section area” vice “cross-sectional area.” Cited definitions were taken primarily from two sources: W.B. -

Glossary of Terms
GLOSSARY OF TERMS For the purpose of this Handbook, the following definitions and abbreviations shall apply. Although all of the definitions and abbreviations listed below may have not been used in this Handbook, the additional terminology is provided to assist the user of Handbook in understanding technical terminology associated with Drainage Improvement Projects and the associated regulations. Program-specific terms have been defined separately for each program and are contained in pertinent sub-sections of Section 2 of this handbook. ACRONYMS ASTM American Society for Testing Materials CBBEL Christopher B. Burke Engineering, Ltd. COE United States Army Corps of Engineers EPA Environmental Protection Agency IDEM Indiana Department of Environmental Management IDNR Indiana Department of Natural Resources NRCS USDA-Natural Resources Conservation Service SWCD Soil and Water Conservation District USDA United States Department of Agriculture USFWS United States Fish and Wildlife Service DEFINITIONS AASHTO Classification. The official classification of soil materials and soil aggregate mixtures for highway construction used by the American Association of State Highway and Transportation Officials. Abutment. The sloping sides of a valley that supports the ends of a dam. Acre-Foot. The volume of water that will cover 1 acre to a depth of 1 ft. Aggregate. (1) The sand and gravel portion of concrete (65 to 75% by volume), the rest being cement and water. Fine aggregate contains particles ranging from 1/4 in. down to that retained on a 200-mesh screen. Coarse aggregate ranges from 1/4 in. up to l½ in. (2) That which is installed for the purpose of changing drainage characteristics.