DOCSLIB.ORG

Chapter 11. Three Dimensional Analytic Geometry and Vectors

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter 11. Three Dimensional Analytic Geometry and Vectors Chapter 11. Three dimensional analytic geometry and vectors. Section 11.5 Quadric surfaces. Curves in R2 : x2 y2 ellipse + =1 a2 b2 x2 y2 hyperbola − =1 a2 b2 parabola y = ax2 or x = by2 A quadric surface is the graph of a second degree equation in three variables. The most general such equation is Ax2 + By2 + Cz2 + Dxy + Exz + F yz + Gx + Hy + Iz + J =0, where A, B, C, ..., J are constants. By translation and rotation the equation can be brought into one of two standard forms Ax2 + By2 + Cz2 + J =0 or Ax2 + By2 + Iz =0 In order to sketch the graph of a quadric surface, it is useful to determine the curves of intersection of the surface with planes parallel to the coordinate planes. These curves are called traces of the surface. Ellipsoids The quadric surface with equation x2 y2 z2 + + =1 a2 b2 c2 is called an ellipsoid because all of its traces are ellipses. 2 1 x y 3 2 1 z ±1 ±2 ±3 ±1 ±2 The six intercepts of the ellipsoid are (±a, 0, 0), (0, ±b, 0), and (0, 0, ±c) and the ellipsoid lies in the box |x| ≤ a, |y| ≤ b, |z| ≤ c Since the ellipsoid involves only even powers of x, y, and z, the ellipsoid is symmetric with respect to each coordinate plane. Example 1. Find the traces of the surface 4x2 +9y2 + 36z2 = 36 1 in the planes x = k, y = k, and z = k. Identify the surface and sketch it. Hyperboloids Hyperboloid of one sheet. The quadric surface with equations x2 y2 z2 1. + − =1 a2 b2 c2 x2 y2 z2 2. − + =1 a2 b2 c2 x2 y2 z2 3. − + + =1 a2 b2 c2 are called hyperbolids of one sheet since two of its traces are hyperbolas and one is an ellipse, and its surface consists of just one piece. 4 2 ±10 ±10 z ±5 ±5 5 5 y x 10 10 ±2 ±4 Example 2. Find the traces of the surface x2 − y2 + z2 =1 in the planes x = k, y = k, and z = k. Identify the surface and sketch it. 2 Hyperboloid of two sheets. The quadric surface with equations x2 y2 z2 1. − − + =1 a2 b2 c2 x2 y2 z2 2. − + − =1 a2 b2 c2 x2 y2 z2 3. − − =1 a2 b2 c2 are called hyperbolids of two sheets since two of its traces are hyperbolas and one is an ellipse, and its surface is two sheets. 10 5 y 5 10 z ±10 ±5 5 10 x ±5 ±10 Example 3. Find the traces of the surface 9x2 − y2 − z2 =9 in the planes x = k, y = k, and z = k. Identify the surface and sketch it. Cone. The quadric surface with equations z2 x2 y2 1. = + c2 a2 b2 y2 x2 z2 2. = + b2 a2 c2 3 x2 y2 z2 3. = + a2 b2 c2 are called cones. 4 x 2 10 5 y ±5 ±10 5 10 ±2 ±4 If P is any point on the cone, then the line OP lies entirely on the cone. The traces in horizontal planes z = k are ellipses and traces in vertical planes x = k or y = k are hyperbolas if k =6 0 but are pairs of lines if k = 0. Paraboloids. The quadric surface with equations z x2 y2 1. = + c a2 b2 y x2 z2 2. = + b a2 c2 x y2 z2 3. = + a b2 c2 are called elliptic paraboloids because its traces in horizontal planes z = k are ellipses, whereas its in vertical planes x = k or y = k are parabolas. 10 8 6 4 2 20 ±10 ±5 5 x y 10 ±20 Example 4. Find the traces of the surface y = x2 + z2 in the planes x = k, y = k, and z = k. Identify the surface and sketch it. 4 The hyperbolic paraboloid z x2 y2 1. = − c a2 b2 y x2 z2 2. = − b a2 c2 x y2 z2 3. = − a b2 c2 also has parabolas as its vertical traces, but its has hyperbolas as its horizontal traces. ±100 ±50 ±10 ±5 ±10 10 5 x y 10 50 100 Quadric cylinders. When one of the variables is missing from the equation of a surface, x2 y2 then the surface is a cylinder. The equation + = 1 represents the elliptic cylinder, the a2 b2 x2 y2 equation − = 1 represents a hyperbolic cylinder, and the equation y = ax2 represents a2 b2 the hyperbolic cylinder. 4 4 4 2 4 2 2 2 ±4 y ±2 z ±5 ±2 ±3 z z ±2 ±1 ±2 ±4 1 2 x 2 2 3 4 ±4 2 y y x 4 x 5 ±2 ±2 ±2 ±4 ±4 ±4 Example 5. Classify the quadric surface 4x2 − y2 + z2 +8x +8z + 24 = 0 and sketch it. 5.
Load more

Recommended publications
  • Analytic Geometry
    Guide Study Georgia End-Of-Course Tests Georgia ANALYTIC GEOMETRY TABLE OF CONTENTS INTRODUCTION ...........................................................................................................5 HOW TO USE THE STUDY GUIDE ................................................................................6 OVERVIEW OF THE EOCT .........................................................................................8 PREPARING FOR THE EOCT ......................................................................................9 Study Skills ........................................................................................................9 Time Management .....................................................................................10 Organization ...............................................................................................10 Active Participation ...................................................................................11 Test-Taking Strategies .....................................................................................11 Suggested Strategies to Prepare for the EOCT ..........................................12 Suggested Strategies the Day before the EOCT ........................................13 Suggested Strategies the Morning of the EOCT ........................................13 Top 10 Suggested Strategies during the EOCT .........................................14 TEST CONTENT ........................................................................................................15
    [Show full text]
  • Quadratic Approximation at a Stationary Point Let F(X, Y) Be a Given
    Multivariable Calculus Grinshpan Quadratic approximation at a stationary point Let f(x; y) be a given function and let (x0; y0) be a point in its domain. Under proper differentiability conditions one has f(x; y) = f(x0; y0) + fx(x0; y0)(x − x0) + fy(x0; y0)(y − y0) 1 2 1 2 + 2 fxx(x0; y0)(x − x0) + fxy(x0; y0)(x − x0)(y − y0) + 2 fyy(x0; y0)(y − y0) + higher−order terms: Let (x0; y0) be a stationary (critical) point of f: fx(x0; y0) = fy(x0; y0) = 0. Then 2 2 f(x; y) = f(x0; y0) + A(x − x0) + 2B(x − x0)(y − y0) + C(y − y0) + higher−order terms, 1 1 1 1 where A = 2 fxx(x0; y0);B = 2 fxy(x0; y0) = 2 fyx(x0; y0), and C = 2 fyy(x0; y0). Assume for simplicity that (x0; y0) = (0; 0) and f(0; 0) = 0. [ This can always be achieved by translation: f~(x; y) = f(x0 + x; y0 + y) − f(x0; y0). ] Then f(x; y) = Ax2 + 2Bxy + Cy2 + higher−order terms. Thus, provided A, B, C are not all zero, the graph of f near (0; 0) resembles the quadric surface z = Ax2 + 2Bxy + Cy2: Generically, this quadric surface is either an elliptic or a hyperbolic paraboloid. We distinguish three scenarios: * Elliptic paraboloid opening up, (0; 0) is a point of local minimum. * Elliptic paraboloid opening down, (0; 0) is a point of local maximum. * Hyperbolic paraboloid, (0; 0) is a saddle point. It should certainly be possible to tell which case we are dealing with by looking at the coefficients A, B, and C, and this is the idea behind the Second Partials Test.
    [Show full text]
  • Pencils of Quadrics
    Europ. J. Combinatorics (1988) 9, 255-270 Intersections in Projective Space II: Pencils of Quadrics A. A. BRUEN AND J. w. P. HIRSCHFELD A complete classification is given of pencils of quadrics in projective space of three dimensions over a finite field, where each pencil contains at least one non-singular quadric and where the base curve is not absolutely irreducible. This leads to interesting configurations in the space such as partitions by elliptic quadrics and by lines. 1. INTRODUCTION A pencil of quadrics in PG(3, q) is non-singular if it contains at least one non-singular quadric. The base of a pencil is a quartic curve and is reducible if over some extension of GF(q) it splits into more than one component: four lines, two lines and a conic, two conics, or a line and a twisted cubic. In order to contain no points or to contain some line over GF(q), the base is necessarily reducible. In the main part of this paper a classification is given of non-singular pencils ofquadrics in L = PG(3, q) with a reducible base. This leads to geometrically interesting configur­ ations obtained from elliptic and hyperbolic quadrics, such as spreads and partitions of L. The remaining part of the paper deals with the case when the base is not reducible and is therefore a rational or elliptic quartic. The number of points in the elliptic case is then governed by the Hasse formula. However, we are able to derive an interesting combi­ natorial relationship, valid also in higher dimensions, between the number of points in the base curve and the number in the base curve of a dual pencil.
    [Show full text]
  • An Introduction to Topology the Classification Theorem for Surfaces by E
    An Introduction to Topology An Introduction to Topology The Classification theorem for Surfaces By E. C. Zeeman Introduction. The classification theorem is a beautiful example of geometric topology. Although it was discovered in the last century*, yet it manages to convey the spirit of present day research. The proof that we give here is elementary, and its is hoped more intuitive than that found in most textbooks, but in none the less rigorous. It is designed for readers who have never done any topology before. It is the sort of mathematics that could be taught in schools both to foster geometric intuition, and to counteract the present day alarming tendency to drop geometry. It is profound, and yet preserves a sense of fun. In Appendix 1 we explain how a deeper result can be proved if one has available the more sophisticated tools of analytic topology and algebraic topology. Examples. Before starting the theorem let us look at a few examples of surfaces. In any branch of mathematics it is always a good thing to start with examples, because they are the source of our intuition. All the following pictures are of surfaces in 3-dimensions. In example 1 by the word “sphere” we mean just the surface of the sphere, and not the inside. In fact in all the examples we mean just the surface and not the solid inside. 1. Sphere. 2. Torus (or inner tube). 3. Knotted torus. 4. Sphere with knotted torus bored through it. * Zeeman wrote this article in the mid-twentieth century. 1 An Introduction to Topology 5.
    [Show full text]
  • Radar Back-Scattering from Non-Spherical Scatterers
    REPORT OF INVESTIGATION NO. 28 STATE OF ILLINOIS WILLIAM G. STRATION, Governor DEPARTMENT OF REGISTRATION AND EDUCATION VERA M. BINKS, Director RADAR BACK-SCATTERING FROM NON-SPHERICAL SCATTERERS PART 1 CROSS-SECTIONS OF CONDUCTING PROLATES AND SPHEROIDAL FUNCTIONS PART 11 CROSS-SECTIONS FROM NON-SPHERICAL RAINDROPS BY Prem N. Mathur and Eugam A. Mueller STATE WATER SURVEY DIVISION A. M. BUSWELL, Chief URBANA. ILLINOIS (Printed by authority of State of Illinois} REPORT OF INVESTIGATION NO. 28 1955 STATE OF ILLINOIS WILLIAM G. STRATTON, Governor DEPARTMENT OF REGISTRATION AND EDUCATION VERA M. BINKS, Director RADAR BACK-SCATTERING FROM NON-SPHERICAL SCATTERERS PART 1 CROSS-SECTIONS OF CONDUCTING PROLATES AND SPHEROIDAL FUNCTIONS PART 11 CROSS-SECTIONS FROM NON-SPHERICAL RAINDROPS BY Prem N. Mathur and Eugene A. Mueller STATE WATER SURVEY DIVISION A. M. BUSWELL, Chief URBANA, ILLINOIS (Printed by authority of State of Illinois) Definitions of Terms Part I semi minor axis of spheroid semi major axis of spheroid wavelength of incident field = a measure of size of particle prolate spheroidal coordinates = eccentricity of ellipse = angular spheroidal functions = Legendse polynomials = expansion coefficients = radial spheroidal functions = spherical Bessel functions = electric field vector = magnetic field vector = back scattering cross section = geometric back scattering cross section Part II = semi minor axis of spheroid = semi major axis of spheroid = Poynting vector = measure of size of spheroid = wavelength of the radiation = back scattering
    [Show full text]
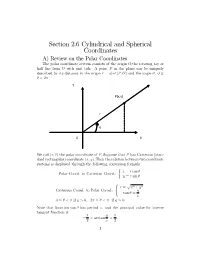
  • Section 2.6 Cylindrical and Spherical Coordinates
    Section 2.6 Cylindrical and Spherical Coordinates A) Review on the Polar Coordinates The polar coordinate system consists of the origin O,the rotating ray or half line from O with unit tick. A point P in the plane can be uniquely described by its distance to the origin r = dist (P, O) and the angle µ, 0 µ < 2¼ : · Y P(x,y) r θ O X We call (r, µ) the polar coordinate of P. Suppose that P has Cartesian (stan- dard rectangular) coordinate (x, y) .Then the relation between two coordinate systems is displayed through the following conversion formula: x = r cos µ Polar Coord. to Cartesian Coord.: y = r sin µ ½ r = x2 + y2 Cartesian Coord. to Polar Coord.: y tan µ = ( p x 0 µ < ¼ if y > 0, 2¼ µ < ¼ if y 0. · · · Note that function tan µ has period ¼, and the principal value for inverse tangent function is ¼ y ¼ < arctan < . ¡ 2 x 2 1 So the angle should be determined by y arctan , if x > 0 xy 8 arctan + ¼, if x < 0 µ = > ¼ x > > , if x = 0, y > 0 < 2 ¼ , if x = 0, y < 0 > ¡ 2 > > Example 6.1. Fin:>d (a) Cartesian Coord. of P whose Polar Coord. is ¼ 2, , and (b) Polar Coord. of Q whose Cartesian Coord. is ( 1, 1) . 3 ¡ ¡ ³ So´l. (a) ¼ x = 2 cos = 1, 3 ¼ y = 2 sin = p3. 3 (b) r = p1 + 1 = p2 1 ¼ ¼ 5¼ tan µ = ¡ = 1 = µ = or µ = + ¼ = . 1 ) 4 4 4 ¡ 5¼ Since ( 1, 1) is in the third quadrant, we choose µ = so ¡ ¡ 4 5¼ p2, is Polar Coord.
    [Show full text]
  • John Ellipsoid 5.1 John Ellipsoid
    CSE 599: Interplay between Convex Optimization and Geometry Winter 2018 Lecture 5: John Ellipsoid Lecturer: Yin Tat Lee Disclaimer: Please tell me any mistake you noticed. The algorithm at the end is unpublished. Feel free to contact me for collaboration. 5.1 John Ellipsoid In the last lecture, we discussed that any convex set is very close to anp ellipsoid in probabilistic sense. More precisely, after renormalization by covariance matrix, we have kxk2 = n ± Θ(1) with high probability. In this lecture, we will talk about how convex set is close to an ellipsoid in a strict sense. If the convex set is isotropic, it is close to a sphere as follows: Theorem 5.1.1. Let K be a convex body in Rn in isotropic position. Then, rn + 1 B ⊆ K ⊆ pn(n + 1)B : n n n Roughly speaking, this says that any convex set can be approximated by an ellipsoid by a n factor. This result has a lot of applications. Although the bound is tight, making a body isotropic is pretty time- consuming. In fact, making a body isotropic is the current bottleneck for obtaining faster algorithm for sampling in convex sets. Currently, it can only be done in O∗(n4) membership oracle plus O∗(n5) total time. Problem 5.1.2. Find a faster algorithm to approximate the covariance matrix of a convex set. In this lecture, we consider another popular position of a convex set called John position and its correspond- ing ellipsoid is called John ellipsoid. Definition 5.1.3. Given a convex set K.
    [Show full text]
  • Calculus & Analytic Geometry
    TQS 126 Spring 2008 Quinn Calculus & Analytic Geometry III Quadratic Equations in 3-D Match each function to its graph 1. 9x2 + 36y2 +4z2 = 36 2. 4x2 +9y2 4z2 =0 − 3. 36x2 +9y2 4z2 = 36 − 4. 4x2 9y2 4z2 = 36 − − 5. 9x2 +4y2 6z =0 − 6. 9x2 4y2 6z =0 − − 7. 4x2 + y2 +4z2 4y 4z +36=0 − − 8. 4x2 + y2 +4z2 4y 4z 36=0 − − − cone • ellipsoid • elliptic paraboloid • hyperbolic paraboloid • hyperboloid of one sheet • hyperboloid of two sheets 24 TQS 126 Spring 2008 Quinn Calculus & Analytic Geometry III Parametric Equations (§10.1) and Vector Functions (§13.1) Definition. If x and y are given as continuous function x = f(t) y = g(t) over an interval of t-values, then the set of points (x, y)=(f(t),g(t)) defined by these equation is a parametric curve (sometimes called aplane curve). The equations are parametric equations for the curve. Often we think of parametric curves as describing the movement of a particle in a plane over time. Examples. x = 2cos t x = et 0 t π 1 t e y = 3sin t ≤ ≤ y = ln t ≤ ≤ Can we find parameterizations of known curves? the line segment circle x2 + y2 =1 from (1, 3) to (5, 1) Why restrict ourselves to only moving through planes? Why not space? And why not use our nifty vector notation? 25 Definition. If x, y, and z are given as continuous functions x = f(t) y = g(t) z = h(t) over an interval of t-values, then the set of points (x,y,z)= (f(t),g(t), h(t)) defined by these equation is a parametric curve (sometimes called a space curve).
    [Show full text]
  • A Quick Algebra Review
    A Quick Algebra Review 1. Simplifying Expressions 2. Solving Equations 3. Problem Solving 4. Inequalities 5. Absolute Values 6. Linear Equations 7. Systems of Equations 8. Laws of Exponents 9. Quadratics 10. Rationals 11. Radicals Simplifying Expressions An expression is a mathematical “phrase.” Expressions contain numbers and variables, but not an equal sign. An equation has an “equal” sign. For example: Expression: Equation: 5 + 3 5 + 3 = 8 x + 3 x + 3 = 8 (x + 4)(x – 2) (x + 4)(x – 2) = 10 x² + 5x + 6 x² + 5x + 6 = 0 x – 8 x – 8 > 3 When we simplify an expression, we work until there are as few terms as possible. This process makes the expression easier to use, (that’s why it’s called “simplify”). The first thing we want to do when simplifying an expression is to combine like terms. For example: There are many terms to look at! Let’s start with x². There Simplify: are no other terms with x² in them, so we move on. 10x x² + 10x – 6 – 5x + 4 and 5x are like terms, so we add their coefficients = x² + 5x – 6 + 4 together. 10 + (-5) = 5, so we write 5x. -6 and 4 are also = x² + 5x – 2 like terms, so we can combine them to get -2. Isn’t the simplified expression much nicer? Now you try: x² + 5x + 3x² + x³ - 5 + 3 [You should get x³ + 4x² + 5x – 2] Order of Operations PEMDAS – Please Excuse My Dear Aunt Sally, remember that from Algebra class? It tells the order in which we can complete operations when solving an equation.
    [Show full text]
  • Automatic Estimation of Sphere Centers from Images of Calibrated Cameras
    Automatic Estimation of Sphere Centers from Images of Calibrated Cameras Levente Hajder 1 , Tekla Toth´ 1 and Zoltan´ Pusztai 1 1Department of Algorithms and Their Applications, Eotv¨ os¨ Lorand´ University, Pazm´ any´ Peter´ stny. 1/C, Budapest, Hungary, H-1117 fhajder,tekla.toth,[email protected] Keywords: Ellipse Detection, Spatial Estimation, Calibrated Camera, 3D Computer Vision Abstract: Calibration of devices with different modalities is a key problem in robotic vision. Regular spatial objects, such as planes, are frequently used for this task. This paper deals with the automatic detection of ellipses in camera images, as well as to estimate the 3D position of the spheres corresponding to the detected 2D ellipses. We propose two novel methods to (i) detect an ellipse in camera images and (ii) estimate the spatial location of the corresponding sphere if its size is known. The algorithms are tested both quantitatively and qualitatively. They are applied for calibrating the sensor system of autonomous cars equipped with digital cameras, depth sensors and LiDAR devices. 1 INTRODUCTION putation and memory costs. Probabilistic Hough Transform (PHT) is a variant of the classical HT: it Ellipse fitting in images has been a long researched randomly selects a small subset of the edge points problem in computer vision for many decades (Prof- which is used as input for HT (Kiryati et al., 1991). fitt, 1982). Ellipses can be used for camera calibra- The 5D parameter space can be divided into two tion (Ji and Hu, 2001; Heikkila, 2000), estimating the pieces. First, the ellipse center is estimated, then the position of parts in an assembly system (Shin et al., remaining three parameters are found in the second 2011) or for defect detection in printed circuit boards stage (Yuen et al., 1989; Tsuji and Matsumoto, 1978).
    [Show full text]
  • Exploding the Ellipse Arnold Good
    Exploding the Ellipse Arnold Good Mathematics Teacher, March 1999, Volume 92, Number 3, pp. 186–188 Mathematics Teacher is a publication of the National Council of Teachers of Mathematics (NCTM). More than 200 books, videos, software, posters, and research reports are available through NCTM’S publication program. Individual members receive a 20% reduction off the list price. For more information on membership in the NCTM, please call or write: NCTM Headquarters Office 1906 Association Drive Reston, Virginia 20191-9988 Phone: (703) 620-9840 Fax: (703) 476-2970 Internet: http://www.nctm.org E-mail: [email protected] Article reprinted with permission from Mathematics Teacher, copyright May 1991 by the National Council of Teachers of Mathematics. All rights reserved. Arnold Good, Framingham State College, Framingham, MA 01701, is experimenting with a new approach to teaching second-year calculus that stresses sequences and series over integration techniques. eaders are advised to proceed with caution. Those with a weak heart may wish to consult a physician first. What we are about to do is explode an ellipse. This Rrisky business is not often undertaken by the professional mathematician, whose polytechnic endeavors are usually limited to encounters with administrators. Ellipses of the standard form of x2 y2 1 5 1, a2 b2 where a > b, are not suitable for exploding because they just move out of view as they explode. Hence, before the ellipse explodes, we must secure it in the neighborhood of the origin by translating the left vertex to the origin and anchoring the left focus to a point on the x-axis.
    [Show full text]
  • Writing the Equation of a Line
    Name______________________________ Writing the Equation of a Line When you find the equation of a line it will be because you are trying to draw scientific information from it. In math, you write equations like y = 5x + 2 This equation is useless to us. You will never graph y vs. x. You will be graphing actual data like velocity vs. time. Your equation should therefore be written as v = (5 m/s2) t + 2 m/s. See the difference? You need to use proper variables and units in order to compare it to theory or make actual conclusions about physical principles. The second equation tells me that when the data collection began (t = 0), the velocity of the object was 2 m/s. It also tells me that the velocity was changing at 5 m/s every second (m/s/s = m/s2). Let’s practice this a little, shall we? Force vs. mass F (N) y = 6.4x + 0.3 m (kg) You’ve just done a lab to see how much force was necessary to get a mass moving along a rough surface. Excel spat out the graph above. You labeled each axis with the variable and units (well done!). You titled the graph starting with the variable on the y-axis (nice job!). Now we turn to the equation. First we replace x and y with the variables we actually graphed: F = 6.4m + 0.3 Then we add units to our slope and intercept. The slope is found by dividing the rise by the run so the units will be the units from the y-axis divided by the units from the x-axis.
    [Show full text]