The Geometry of the Phase Diffusion Equation
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Chapter 11. Three Dimensional Analytic Geometry and Vectors
Chapter 11. Three dimensional analytic geometry and vectors. Section 11.5 Quadric surfaces. Curves in R2 : x2 y2 ellipse + =1 a2 b2 x2 y2 hyperbola − =1 a2 b2 parabola y = ax2 or x = by2 A quadric surface is the graph of a second degree equation in three variables. The most general such equation is Ax2 + By2 + Cz2 + Dxy + Exz + F yz + Gx + Hy + Iz + J =0, where A, B, C, ..., J are constants. By translation and rotation the equation can be brought into one of two standard forms Ax2 + By2 + Cz2 + J =0 or Ax2 + By2 + Iz =0 In order to sketch the graph of a quadric surface, it is useful to determine the curves of intersection of the surface with planes parallel to the coordinate planes. These curves are called traces of the surface. Ellipsoids The quadric surface with equation x2 y2 z2 + + =1 a2 b2 c2 is called an ellipsoid because all of its traces are ellipses. 2 1 x y 3 2 1 z ±1 ±2 ±3 ±1 ±2 The six intercepts of the ellipsoid are (±a, 0, 0), (0, ±b, 0), and (0, 0, ±c) and the ellipsoid lies in the box |x| ≤ a, |y| ≤ b, |z| ≤ c Since the ellipsoid involves only even powers of x, y, and z, the ellipsoid is symmetric with respect to each coordinate plane. Example 1. Find the traces of the surface 4x2 +9y2 + 36z2 = 36 1 in the planes x = k, y = k, and z = k. Identify the surface and sketch it. Hyperboloids Hyperboloid of one sheet. The quadric surface with equations x2 y2 z2 1. -

A Quick Algebra Review
A Quick Algebra Review 1. Simplifying Expressions 2. Solving Equations 3. Problem Solving 4. Inequalities 5. Absolute Values 6. Linear Equations 7. Systems of Equations 8. Laws of Exponents 9. Quadratics 10. Rationals 11. Radicals Simplifying Expressions An expression is a mathematical “phrase.” Expressions contain numbers and variables, but not an equal sign. An equation has an “equal” sign. For example: Expression: Equation: 5 + 3 5 + 3 = 8 x + 3 x + 3 = 8 (x + 4)(x – 2) (x + 4)(x – 2) = 10 x² + 5x + 6 x² + 5x + 6 = 0 x – 8 x – 8 > 3 When we simplify an expression, we work until there are as few terms as possible. This process makes the expression easier to use, (that’s why it’s called “simplify”). The first thing we want to do when simplifying an expression is to combine like terms. For example: There are many terms to look at! Let’s start with x². There Simplify: are no other terms with x² in them, so we move on. 10x x² + 10x – 6 – 5x + 4 and 5x are like terms, so we add their coefficients = x² + 5x – 6 + 4 together. 10 + (-5) = 5, so we write 5x. -6 and 4 are also = x² + 5x – 2 like terms, so we can combine them to get -2. Isn’t the simplified expression much nicer? Now you try: x² + 5x + 3x² + x³ - 5 + 3 [You should get x³ + 4x² + 5x – 2] Order of Operations PEMDAS – Please Excuse My Dear Aunt Sally, remember that from Algebra class? It tells the order in which we can complete operations when solving an equation. -

Writing the Equation of a Line
Name______________________________ Writing the Equation of a Line When you find the equation of a line it will be because you are trying to draw scientific information from it. In math, you write equations like y = 5x + 2 This equation is useless to us. You will never graph y vs. x. You will be graphing actual data like velocity vs. time. Your equation should therefore be written as v = (5 m/s2) t + 2 m/s. See the difference? You need to use proper variables and units in order to compare it to theory or make actual conclusions about physical principles. The second equation tells me that when the data collection began (t = 0), the velocity of the object was 2 m/s. It also tells me that the velocity was changing at 5 m/s every second (m/s/s = m/s2). Let’s practice this a little, shall we? Force vs. mass F (N) y = 6.4x + 0.3 m (kg) You’ve just done a lab to see how much force was necessary to get a mass moving along a rough surface. Excel spat out the graph above. You labeled each axis with the variable and units (well done!). You titled the graph starting with the variable on the y-axis (nice job!). Now we turn to the equation. First we replace x and y with the variables we actually graphed: F = 6.4m + 0.3 Then we add units to our slope and intercept. The slope is found by dividing the rise by the run so the units will be the units from the y-axis divided by the units from the x-axis. -

Numerical Algebraic Geometry and Algebraic Kinematics
Numerical Algebraic Geometry and Algebraic Kinematics Charles W. Wampler∗ Andrew J. Sommese† January 14, 2011 Abstract In this article, the basic constructs of algebraic kinematics (links, joints, and mechanism spaces) are introduced. This provides a common schema for many kinds of problems that are of interest in kinematic studies. Once the problems are cast in this algebraic framework, they can be attacked by tools from algebraic geometry. In particular, we review the techniques of numerical algebraic geometry, which are primarily based on homotopy methods. We include a review of the main developments of recent years and outline some of the frontiers where further research is occurring. While numerical algebraic geometry applies broadly to any system of polynomial equations, algebraic kinematics provides a body of interesting examples for testing algorithms and for inspiring new avenues of work. Contents 1 Introduction 4 2 Notation 5 I Fundamentals of Algebraic Kinematics 6 3 Some Motivating Examples 6 3.1 Serial-LinkRobots ............................... ..... 6 3.1.1 Planar3Rrobot ................................. 6 3.1.2 Spatial6Rrobot ................................ 11 3.2 Four-BarLinkages ................................ 13 3.3 PlatformRobots .................................. 18 ∗General Motors Research and Development, Mail Code 480-106-359, 30500 Mound Road, Warren, MI 48090- 9055, U.S.A. Email: [email protected] URL: www.nd.edu/˜cwample1. This material is based upon work supported by the National Science Foundation under Grant DMS-0712910 and by General Motors Research and Development. †Department of Mathematics, University of Notre Dame, Notre Dame, IN 46556-4618, U.S.A. Email: [email protected] URL: www.nd.edu/˜sommese. This material is based upon work supported by the National Science Foundation under Grant DMS-0712910 and the Duncan Chair of the University of Notre Dame. -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential -

Chapter 1: Analytic Geometry
1 Analytic Geometry Much of the mathematics in this chapter will be review for you. However, the examples will be oriented toward applications and so will take some thought. In the (x,y) coordinate system we normally write the x-axis horizontally, with positive numbers to the right of the origin, and the y-axis vertically, with positive numbers above the origin. That is, unless stated otherwise, we take “rightward” to be the positive x- direction and “upward” to be the positive y-direction. In a purely mathematical situation, we normally choose the same scale for the x- and y-axes. For example, the line joining the origin to the point (a,a) makes an angle of 45◦ with the x-axis (and also with the y-axis). In applications, often letters other than x and y are used, and often different scales are chosen in the horizontal and vertical directions. For example, suppose you drop something from a window, and you want to study how its height above the ground changes from second to second. It is natural to let the letter t denote the time (the number of seconds since the object was released) and to let the letter h denote the height. For each t (say, at one-second intervals) you have a corresponding height h. This information can be tabulated, and then plotted on the (t, h) coordinate plane, as shown in figure 1.0.1. We use the word “quadrant” for each of the four regions into which the plane is divided by the axes: the first quadrant is where points have both coordinates positive, or the “northeast” portion of the plot, and the second, third, and fourth quadrants are counted off counterclockwise, so the second quadrant is the northwest, the third is the southwest, and the fourth is the southeast. -

The Evolution of Equation-Solving: Linear, Quadratic, and Cubic
California State University, San Bernardino CSUSB ScholarWorks Theses Digitization Project John M. Pfau Library 2006 The evolution of equation-solving: Linear, quadratic, and cubic Annabelle Louise Porter Follow this and additional works at: https://scholarworks.lib.csusb.edu/etd-project Part of the Mathematics Commons Recommended Citation Porter, Annabelle Louise, "The evolution of equation-solving: Linear, quadratic, and cubic" (2006). Theses Digitization Project. 3069. https://scholarworks.lib.csusb.edu/etd-project/3069 This Thesis is brought to you for free and open access by the John M. Pfau Library at CSUSB ScholarWorks. It has been accepted for inclusion in Theses Digitization Project by an authorized administrator of CSUSB ScholarWorks. For more information, please contact [email protected]. THE EVOLUTION OF EQUATION-SOLVING LINEAR, QUADRATIC, AND CUBIC A Project Presented to the Faculty of California State University, San Bernardino In Partial Fulfillment of the Requirements for the Degre Master of Arts in Teaching: Mathematics by Annabelle Louise Porter June 2006 THE EVOLUTION OF EQUATION-SOLVING: LINEAR, QUADRATIC, AND CUBIC A Project Presented to the Faculty of California State University, San Bernardino by Annabelle Louise Porter June 2006 Approved by: Shawnee McMurran, Committee Chair Date Laura Wallace, Committee Member , (Committee Member Peter Williams, Chair Davida Fischman Department of Mathematics MAT Coordinator Department of Mathematics ABSTRACT Algebra and algebraic thinking have been cornerstones of problem solving in many different cultures over time. Since ancient times, algebra has been used and developed in cultures around the world, and has undergone quite a bit of transformation. This paper is intended as a professional developmental tool to help secondary algebra teachers understand the concepts underlying the algorithms we use, how these algorithms developed, and why they work. -
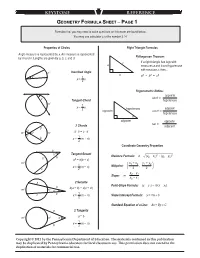
Geometry Formula Sheet ─ Page 1
KEYSTONE RefEFERENCE GEOMETRY FORMULA SHEET ─ PAGE 1 Formulas that you may need to solve questions on this exam are found below. You may use calculator π or the number 3.14. Properties of Circles Right Triangle Formulas Angle measure is represented by x. Arc measure is represented Pythagorean Theorem: by m and n. Lengths are given by a, b, c, and d. c If a right triangle has legs with a measures a and b and hypotenuse with measure c, then... n° Inscribed Angle b 2 + 2 = 2 x° 1 a b c x = n 2 Trigonometric Ratios: opposite sin θ = x° Tangent-Chord hypotenuse n° = 1 x n hypotenuse adjacent 2 opposite cos θ = hypotenuse θ adjacent opposite tan θ = 2 Chords adjacent d a · = · m°x° n° a b c d c 1 b x = (m + n) 2 Coordinate Geometry Properties a x° Tangent-Secant = – 2 + – 2 b Distance Formula: d (x2 x 1) (y2 y 1) n° 2 = + a b (b c) m° x + x y + y 1 1 2 , 1 2 x = (m − n) Midpoint: c 2 2 2 y − y = 2 1 Slope: m − x 2 x 1 a 2 Secants Point-Slope Formula: (y − y ) = m(x − x ) b + = + 1 1 b (a b) d (c d ) m° n° x° 1 c d x = (m − n) Slope Intercept Formula: y = mx + b 2 Standard Equation of a Line: Ax + By = C a 2 Tangents a = b m° n° x° 1 x = (m − n) b 2 Copyright © 2011 by the Pennsylvania Department of Education. The materials contained in this publication may be duplicated by Pennsylvania educators for local classroom use. -

Analytic Geometry
INTRODUCTION TO ANALYTIC GEOMETRY BY PEECEY R SMITH, PH.D. N PROFESSOR OF MATHEMATICS IN THE SHEFFIELD SCIENTIFIC SCHOOL YALE UNIVERSITY AND AKTHUB SULLIVAN GALE, PH.D. ASSISTANT PROFESSOR OF MATHEMATICS IN THE UNIVERSITY OF ROCHESTER GINN & COMPANY BOSTON NEW YORK CHICAGO LONDON COPYRIGHT, 1904, 1905, BY ARTHUR SULLIVAN GALE ALL BIGHTS RESERVED 65.8 GINN & COMPANY PRO- PRIETORS BOSTON U.S.A. PEE FACE In preparing this volume the authors have endeavored to write a drill book for beginners which presents, in a manner conform- ing with modern ideas, the fundamental concepts of the subject. The subject-matter is slightly more than the minimum required for the calculus, but only as much more as is necessary to permit of some choice on the part of the teacher. It is believed that the text is complete for students finishing their study of mathematics with a course in Analytic Geometry. The authors have intentionally avoided giving the book the form of a treatise on conic sections. Conic sections naturally appear, but chiefly as illustrative of general analytic methods. Attention is called to the method of treatment. The subject is developed after the Euclidean method of definition and theorem, without, however, adhering to formal presentation. The advan- tage is obvious, for the student is made sure of the exact nature of each acquisition. Again, each method is summarized in a rule stated in consecutive steps. This is a gain in clearness. Many illustrative examples are worked out in the text. Emphasis has everywhere been put upon the analytic side, that is, the student is taught to start from the equation. -

Asce Standardized Reference Evapotranspiration Equation
THE ASCE STANDARDIZED REFERENCE EVAPOTRANSPIRATION EQUATION Task Committee on Standardization of Reference Evapotranspiration Environmental and Water Resources Institute of the American Society of Civil Engineers January, 2005 Final Report ASCE Standardized Reference Evapotranspiration Equation Page i THE ASCE STANDARDIZED REFERENCE EVAPOTRANSPIRATION EQUATION PREPARED BY Task Committee on Standardization of Reference Evapotranspiration of the Environmental and Water Resources Institute TASK COMMITTEE MEMBERS Ivan A. Walter (chair), Richard G. Allen (vice-chair), Ronald Elliott, Daniel Itenfisu, Paul Brown, Marvin E. Jensen, Brent Mecham, Terry A. Howell, Richard Snyder, Simon Eching, Thomas Spofford, Mary Hattendorf, Derrell Martin, Richard H. Cuenca, and James L. Wright PRINCIPAL EDITORS Richard G. Allen, Ivan A. Walter, Ronald Elliott, Terry Howell, Daniel Itenfisu, Marvin Jensen ENDORSEMENTS Irrigation Association, 2004 ASCE-EWRI Task Committee Report, January, 2005 ASCE Standardized Reference Evapotranspiration Equation Page ii ABSTRACT This report describes the standardization of calculation of reference evapotranspiration (ET) as recommended by the Task Committee on Standardization of Reference Evapotranspiration of the Environmental and Water Resources Institute of the American Society of Civil Engineers. The purpose of the standardized reference ET equation and calculation procedures is to bring commonality to the calculation of reference ET and to provide a standardized basis for determining or transferring crop coefficients for agricultural and landscape use. The basis of the standardized reference ET equation is the ASCE Penman-Monteith (ASCE-PM) method of ASCE Manual 70. For the standardization, the ASCE-PM method is applied for two types of reference surfaces representing clipped grass (a short, smooth crop) and alfalfa (a taller, rougher agricultural crop), and the equation is simplified to a reduced form of the ASCE–PM. -

The Roots of Any Polynomial Equation
The roots of any polynomial equation G.A.Uytdewilligen, Bergen op Zoomstraat 76, 5652 KE Eindhoven. [email protected] Abstract We provide a method for solving the roots of the general polynomial equation n n−1 a ⋅x + a ⋅x + . + a ⋅x + s 0 n n−1 1 (1) To do so, we express x as a powerseries of s, and calculate the first n-1 coefficients. We turn the polynomial equation into a differential equation that has the roots as solutions. Then we express the powerseries’ coefficients in the first n-1 coefficients. Then the variable s is set to a0. A free parameter is added to make the series convergent. © 2004 G.A.Uytdewilligen. All rights reserved. Keywords: Algebraic equation The method The method is based on [1]. Let’s take the first n-1 derivatives of (1) to s. Equate these derivatives to zero. di Then find x ( s ) in terms of x(s) for i from 1 to n-1. Now make a new differential equation dsi n 1 n 2 d − d − m1⋅ x(s) + m2⋅ x(s) + . + m ⋅x(s) + m 0 n−1 n−2 n n+1 ds ds (2) di and fill in our x ( s ) in (2). Multiply by the denominator of the expression. Now we have a dsi polynomial in x(s) of degree higher then n. Using (1) as property, we simplify this polynomial to the degree of n. Set it equal to (1) and solve m1 .. mn+1 in terms of s and a1 .. an Substituting these in (2) gives a differential equation that has the zeros of (1) among its solutions. -

The Schrödinger Equation on a Compact Manifold : Strichartz Estimates and Applications
Journées Équations aux dérivées partielles Plestin-les-grèves, 5–8 juin 2002 GDR 1151 (CNRS) The Schrödinger equation on a compact manifold : Strichartz estimates and applications Nicolas Burq Patrick Gérard Nikolay Tzvetkov Résumé Nous établissons des estimations de Strichartz avec perte de derivée frac- tionnaire pour l’équation de Schrödinger sur toute variété riemannienne com- pacte. Nous en deduisons des théorèmes d’existence globale pour le problème de Cauchy d’équations de Schrödinger non–linéaires sur les surfaces dans le cas de non–linéarités polynomiales défocalisantes, et sur les variétés de dimension trois dans le cas de non–linéarités quadratiques. Nous discutons également l’optimalité de ces estimées de Strichartz sur les sphères. Abstract We prove Strichartz estimates with fractional loss of derivatives for the Schrödinger equation on any riemannian compact manifold. As a conse- quence we infer global existence results for the Cauchy problem of nonlinear Schrödinger equations on surfaces in the case of defocusing polynomial non- linearities, and on three–manifolds in the case of quadratic nonlinearities. We also discuss the optimality of these Strichartz estimates on spheres. 1. Introduction Let (M, g) be a complete riemannian manifold. The nonlinear Schrödinger equation on M reads 0 2 i∂tu + ∆gu = P (|u| )u, u(0, x) = u0(x). (1.1) where ∆g denotes the Laplace–Beltrami operator on M, and P : R+ → R is a (at least C1) function, for instance polynomial. It is classical that equation (1.1) satisfies the following formal conservation laws : ku(t)kL2 = ku0kL2 (1.2) We thank H. Koch and S. Zelditch for discussions about the optimality of our results on spheres and Zoll manifolds, and E.