Fast Generation of Planar Graphs (Expanded Version)
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
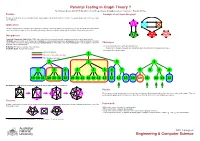
Parental Testing in Graph Theory?
Parental Testing in Graph Theory ? By S Narjess Afzaly,∗ ANU CSIT Algorithm & Data Group, [email protected]. Supervisor: Brendan McKay.∗ Problem A sample of an irreducible graph To make a complete list of non-isomorphic simple quartic graphs with the given number of vertices. In a quartic graph, each vertex has exactly four neighbours. Applications Finding counterexamples, verifying some conjectures or refining some proofs whether in graph theory or in any other field where the problem can be modelled as a graph such as: chemistry, web mining, national security, the railway map, the electrical circuit and neural science. Our approach Canonical Construction Path (McKay 1998): A general method to recursively generate combinatorial objects in which larger objects, (Children), are constructed out of smaller ones, (Parents), by some well-defined operation, (extension), and avoiding constructing isomorphic copies at each construction step by defining a unique genuine parent for each graph. Hence a generated graph is only accepted if it has been Challenges extended from its genuine parent. • To avoid isomorphic copies when generating the list: Reduction: The inverse operation of the extension. Irreducible graph: A graph with no parent. The definition of the genuine parent can substantially affect the efficiency of the generation process. • Generating all irreducible graphs. Genuine parent 1 Has an isomorphic sibling Not genuine parent 2 2 3 4 5 5 6 5 5 6 6 7 5 8 9 6 10 10 11 10 10 11 12 10 10 11 10 10 11 12 12 12 13 10 10 11 10 13 12 Our Reduction: Deleting a vertex and adding two extra disjoint edges between its neighbours. -

Smallest Cubic and Quartic Graphs with a Given Number of Cutpoints and Bridges Gary Chartrand
Old Dominion University ODU Digital Commons Mathematics & Statistics Faculty Publications Mathematics & Statistics 1982 Smallest Cubic and Quartic Graphs With a Given Number of Cutpoints and Bridges Gary Chartrand Farrokh Saba John K. Cooper Jr. Frank Harary Curtiss E. Wall Old Dominion University Follow this and additional works at: https://digitalcommons.odu.edu/mathstat_fac_pubs Part of the Mathematics Commons Repository Citation Chartrand, Gary; Saba, Farrokh; Cooper, John K. Jr.; Harary, Frank; and Wall, Curtiss E., "Smallest Cubic and Quartic Graphs With a Given Number of Cutpoints and Bridges" (1982). Mathematics & Statistics Faculty Publications. 76. https://digitalcommons.odu.edu/mathstat_fac_pubs/76 Original Publication Citation Chartrand, G., Saba, F., Cooper, J. K., Harary, F., & Wall, C. E. (1982). Smallest cubic and quartic graphs with a given number of cutpoints and bridges. International Journal of Mathematics and Mathematical Sciences, 5(1), 41-48. doi:10.1155/s0161171282000052 This Article is brought to you for free and open access by the Mathematics & Statistics at ODU Digital Commons. It has been accepted for inclusion in Mathematics & Statistics Faculty Publications by an authorized administrator of ODU Digital Commons. For more information, please contact [email protected]. I nternat. J. Math. & Math. Sci. Vol. 5 No. (1982)41-48 41 SMALLEST CUBIC AND QUARTIC GRAPHS WITH A GIVEN NUMBER OF CUTPOINTS AND BRIDGES GARY CHARTRAND and FARROKH SABA Department of Mathematics, Western Michigan University Kalamazoo, Michigan 49008 U. S .A. JOHN K. COOPER, JR. Department of Mathematics, Eastern Michigan University Ypsilanti, Michigan 48197 U.S.A. FRANK HARARY Department of Mathematics, University of Michigan Ann Arbor, Michigan 48104 U.S.A. -

Distance-Two Colorings of Barnette Graphs
CCCG 2018, Winnipeg, Canada, August 8{10, 2018 Distance-Two Colorings of Barnette Graphs Tom´asFeder∗ Pavol Helly Carlos Subiz Abstract that the conjectures hold on the intersection of the two classes, i.e., that tri-connected cubic planar graphs with Barnette identified two interesting classes of cubic poly- all face sizes 4 or 6 are Hamiltonian. When all faces hedral graphs for which he conjectured the existence of have sizes 5 or 6, this was a longstanding open prob- a Hamiltonian cycle. Goodey proved the conjecture for lem, especially since these graphs (tri-connected cubic the intersection of the two classes. We examine these planar graphs with all face sizes 5 or 6) are the popu- classes from the point of view of distance-two color- lar fullerene graphs [8]. The second conjecture has now ings. A distance-two r-coloring of a graph G is an as- been affirmatively resolved in full [18]. For the first con- signment of r colors to the vertices of G so that any jecture, two of the present authors have shown in [10] two vertices at distance at most two have different col- that if the conjecture is false, then the Hamiltonicity ors. Note that a cubic graph needs at least four colors. problem for tri-connected cubic planar graphs is NP- The distance-two four-coloring problem for cubic planar complete. In view of these results and conjectures, in graphs is known to be NP-complete. We claim the prob- this paper we call bipartite tri-connected cubic planar lem remains NP-complete for tri-connected bipartite graphs type-one Barnette graphs; we call cubic plane cubic planar graphs, which we call type-one Barnette graphs with all face sizes 3; 4; 5 or 6 type-two Barnette graphs, since they are the first class identified by Bar- graphs; and finally we call cubic plane graphs with all nette. -

Energy Landscapes for the Self-Assembly of Supramolecular Polyhedra
JNonlinearSci DOI 10.1007/s00332-016-9286-9 Energy Landscapes for the Self-Assembly of Supramolecular Polyhedra Emily R. Russell1 Govind Menon2 · Received: 16 June 2015 / Accepted: 23 January 2016 ©SpringerScience+BusinessMediaNewYork2016 Abstract We develop a mathematical model for the energy landscape of polyhedral supramolecular cages recently synthesized by self-assembly (Sun et al. in Science 328:1144–1147, 2010). Our model includes two essential features of the experiment: (1) geometry of the organic ligands and metallic ions; and (2) combinatorics. The molecular geometry is used to introduce an energy that favors square-planar vertices 2 (modeling Pd + ions) and bent edges with one of two preferred opening angles (model- ing boomerang-shaped ligands of two types). The combinatorics of the model involve two-colorings of edges of polyhedra with four-valent vertices. The set of such two- colorings, quotiented by the octahedral symmetry group, has a natural graph structure and is called the combinatorial configuration space. The energy landscape of our model is the energy of each state in the combinatorial configuration space. The challenge in the computation of the energy landscape is a combinatorial explosion in the number of two-colorings of edges. We describe sampling methods based on the symmetries Communicated by Robert V. Kohn. ERR acknowledges the support and hospitality of the Institute for Computational and Experimental Research in Mathematics (ICERM) at Brown University, where she was a postdoctoral fellow while carrying out this work. GM acknowledges partial support from NSF grant DMS 14-11278. This research was conducted using computational resources at the Center for Computation and Visualization, Brown University. -

Quartic Planar Graphs
Quartic planar graphs Jane Tan October 2018 A thesis submitted for the degree of Bachelor of Philosophy (Honours) of the Australian National University Declaration The work in this thesis is my own except where otherwise stated. Jane Tan Acknowledgements First, I'd like to thank my supervisors, Brendan McKay and Scott Morrison. Brendan { your guidance has been invaluable. I'm so grateful for all of the exciting problems you've introduced me to, and that you're still putting up with me a full two years after you agreed to take me on \just for one semester". And Scott { thank you for your help with editing, your calming presence, and for sharing the good chalk. I would also like to thank all of the lecturers at the MSI who have been so generous with their time and from whom I have learnt so much. Special thanks to Vigleik, Joan and Andrew for teaching fantastic reading courses and supervising me in projects over the years. Thanks also go to all of the honours students, even the cookie monster and the elusive north-siders. It's been great fun sharing our shiny new office! Last but not least, thank you to my family for always being on the phone. v Abstract In this thesis, we explore three problems concerning quartic planar graphs. The first is on recursive structures; we prove generation theorems for several interest- ing subclasses of quartic planar graphs and their duals, building on previous work which has largely been focussed on the simple or nonplanar cases. The second problem is on the existence of locally self-avoiding Eulerian circuits. -

Exploring Multistability in Prismatic Metamaterials Through Local Actuation
ARTICLE https://doi.org/10.1038/s41467-019-13319-7 OPEN Exploring multistability in prismatic metamaterials through local actuation Agustin Iniguez-Rabago 1, Yun Li 1 & Johannes T.B. Overvelde 1* Metamaterials are artificial materials that derive their unusual properties from their periodic architecture. Some metamaterials can deform their internal structure to switch between different properties. However, the precise control of these deformations remains a challenge, 1234567890():,; as these structures often exhibit non-linear mechanical behavior. We introduce a compu- tational and experimental strategy to explore the folding behavior of a range of 3D prismatic building blocks that exhibit controllable multifunctionality. By applying local actuation pat- terns, we are able to explore and visualize their complex mechanical behavior. We find a vast and discrete set of mechanically stable configurations, that arise from local minima in their elastic energy. Additionally these building blocks can be assembled into metamaterials that exhibit similar behavior. The mechanical principles on which the multistable behavior is based are scale-independent, making our designs candidates for e.g., reconfigurable acoustic wave guides, microelectronic mechanical systems and energy storage systems. 1 AMOLF, Science Park 104, 1098 XG Amsterdam, Netherlands. *email: [email protected] NATURE COMMUNICATIONS | (2019) 10:5577 | https://doi.org/10.1038/s41467-019-13319-7 | www.nature.com/naturecommunications 1 ARTICLE NATURE COMMUNICATIONS | https://doi.org/10.1038/s41467-019-13319-7 n the search for materials with exotic properties, researchers polyhedron in the direction normal to the corresponding face have recently started to explore the design of their mesoscopic (Fig. 1). When assuming rigid origami29 (i.e., the structure can I 1 architecture . -

G-Graphs: a New Representation of Groups
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Journal of Symbolic Computation 42 (2007) 549–560 www.elsevier.com/locate/jsc G-graphs: A new representation of groups Alain Brettoa,∗, Alain Faisantb, Luc Gilliberta a Universite´ de Caen, GREYC CNRS UMR-6072. Campus 2, Bd Marechal Juin BP 5186, 14032 Caen cedex, France b Universite´ Jean Monnet LARAL 23 rue Paul Michelon, 42023 Saint-Etienne cedex 2, France Received 31 October 2004; accepted 8 August 2006 Available online 5 March 2007 Abstract An important part of computer science is focused on the links that can be established between group theory and graph theory and graphs. CAYLEY graphs, that establish such a link, are useful in a lot of areas of sciences. This paper introduces a new type of graph associated with a group, the G-graphs, and presents many of their properties. We show that various characteristics of a group can be seen on its associated G-graph. We also present an implementation of the algorithm constructing these new graphs, an implementation that will lead to some experimental results. Finally we show that many classical graphs are G-graphs. The relations between G-graphs and CAYLEY graphs are also studied. c 2007 Elsevier Ltd. All rights reserved. Keywords: Computational group theory; Graph representation of a group; Cayley graphs; G-graphs 1. Introduction Group theory can be considered as the study of symmetry. A group is basically the collection of symmetries of some object preserving some of its structure; therefore many sciences have to deal with groups. -

Distance-Two Colorings of Barnette Graphs
DISTANCE-TWO COLORINGS OF BARNETTE GRAPHS TOMAS´ FEDER, PAVOL HELL, AND CARLOS SUBI Abstract. Barnette identified two interesting classes of cubic polyhedral graphs for which he conjectured the existence of a Hamiltonian cycle. Goodey proved the conjecture for the intersection of the two classes. We examine these classes from the point of view of distance- two colorings. A distance-two r-coloring of a graph G is an assignment of r colors to the vertices of G so that any two vertices at distance at most two have different colors. Note that a cubic graph needs at least four colors. The distance-two four-coloring problem for cubic planar graphs is known to be NP-complete. We claim the problem remains NP-complete for tri-connected bipartite cubic planar graphs, which we call type-one Barnette graphs, since they are the first class identified by Barnette. By contrast, we claim the problem is polynomial for cubic plane graphs with face sizes 3; 4; 5; or 6, which we call type-two Barnette graphs, because of their relation to Barnette's second conjecture. We call Goodey graphs those type- two Barnette graphs all of whose faces have size 4 or 6. We fully describe all Goodey graphs that admit a distance-two four-coloring, and characterize the remaining type-two Barnette graphs that admit a distance-two four-coloring according to their face size. For quartic plane graphs, the analogue of type-two Barnette graphs are graphs with face sizes 3 or 4. For this class, the distance-two four-coloring problem is also polynomial; in fact, we can again fully describe all colorable instances { there are exactly two such graphs. -

A Note on Coloring of 3/3-Power of Subquartic Graphs
AUSTRALASIAN JOURNAL OF COMBINATORICS Volume 79(3) (2021), Pages 454{460 3 A note on coloring of 3-power of subquartic graphs Mahsa Mozafari-Nia Moharram N. Iradmusa Department of Mathematical Sciences Shahid Beheshti University G.C. P.O. Box 19839-63113, Tehran Iran Abstract 1 For any k 2 N, the k-subdivision of a graph G is a simple graph G k , which is constructed by replacing each edge of G with a path of length k. In [M.N. Iradmusa, Discrete Math. 310 (10-11) (2010), 1551{1556], the mth power of the n-subdivision of G was introduced as a fractional m power of G, denoted by G n . F. Wang and X. Liu in [Discrete Math. 3 Algorithms Appl. 10 (3), (2018), 1850041] showed that χ(G 3 ) ≤ 7 for 3 any subcubic graph G. In this note, we prove that the 3 -power of every subquartic graph admits a proper coloring with at most nine colors. We 3 conjecture that χ(G 3 ) ≤ 2∆(G) + 1 for any graph G with maximum degree ∆(G) ≥ 2. 1 Introduction All graphs we consider in this note are simple, finite and undirected. We men- tion some of the definitions that are referred to throughout this note, and for other necessary definitions and notation we refer the reader to a standard text-book [2]. Minimum degree, maximum degree and maximum size of cliques of a graph G are denoted by δ(G), ∆(G) and !(G), respectively. For each vertex v 2 V (G), the neigh- bors of v are the vertices adjacent to v in G. -

On Quartic Half-Arc-Transitive Metacirculants
J Algebr Comb (2008) 28: 365–395 DOI 10.1007/s10801-007-0107-y On quartic half-arc-transitive metacirculants Dragan Marušicˇ · Primož Šparl Received: 7 June 2007 / Accepted: 6 November 2007 / Published online: 5 December 2007 © Springer Science+Business Media, LLC 2007 Abstract Following Alspach and Parsons, a metacirculant graph is a graph admit- ting a transitive group generated by two automorphisms ρ and σ , where ρ is (m, n)- semiregular for some integers m ≥ 1, n ≥ 2, and where σ normalizes ρ, cyclically permuting the orbits of ρ in such a way that σ m has at least one fixed vertex. A half- arc-transitive graph is a vertex- and edge- but not arc-transitive graph. In this arti- cle quartic half-arc-transitive metacirculants are explored and their connection to the so called tightly attached quartic half-arc-transitive graphs is explored. It is shown that there are three essentially different possibilities for a quartic half-arc-transitive metacirculant which is not tightly attached to exist. These graphs are extensively studied and some infinite families of such graphs are constructed. Keywords Graph · Metacirculant graph · Half-arc-transitive · Tightly attached · Automorphism group 1 Introductory and historic remarks Throughout this paper graphs are assumed to be finite and, unless stated otherwise, simple, connected and undirected (but with an implicit orientation of the edges when appropriate). For group-theoretic concepts not defined here we refer the reader to [4, 9, 34], and for graph-theoretic terms not defined here we refer the reader to [5]. Both authors were supported in part by “ARRS – Agencija za znanost Republike Slovenije”, program no. -

Geometric Realizations of Cyclically Branched Coverings Over Punctured Spheres
Geometric realizations of cyclically branched coverings over punctured spheres Dami Lee Abstract In classical differential geometry, a central question has been whether abstract sur- faces with given geometric features can be realized as surfaces in Euclidean space. Inspired by the rich theory of embedded triply periodic minimal surfaces, we seek ex- amples of triply periodic polyhedral surfaces that have an identifiable conformal struc- ture. In particular, we are interested in explicit cone metrics on compact Riemann surfaces that have a realization as the quotient of a triply periodic polyhedral surface. This is important as Riemann surfaces where one has equivalent descriptions are rare. We construct periodic surfaces using graph theory as an attempt to make Schoens heuristic concept of a dual graph rigorous. We then apply the theory of cyclically branched coverings to identify the conformal type of such surfaces. Contents 1 Introduction 2 2 A Regular Triply Periodic Polyhedral Surface 4 3 Cyclically Branched Covers Over Spheres 7 3.1 Construction of cyclically branched covers over spheres . .7 3.2 Maps between cyclically branched covers . 11 3.3 Cone metrics on punctured spheres . 13 3.4 Wronski metric and Weierstrass points . 18 arXiv:1809.06321v1 [math.DG] 17 Sep 2018 4 Regular Triply Periodic Polyhedral Surfaces 21 4.1 Triply periodic symmetric skeletal graphs . 22 4.2 Classification of regular triply periodic polyhedral surfaces . 24 5 Conformal Structures of Regular Triply Periodic Polyhedral Surfaces 29 5.1 Mucube, Muoctahedron, and Mutetrahedron . 30 5.2 Octa-8 . 34 5.3 Truncated Octa-8 . 36 5.4 Octa-4 . 37 6 Figure Credits 39 1 A All cyclically branched covers up to genus five 40 B Wronski computation for the Octa-4 surface 42 Bibliography 43 1 Introduction In classical differential geometry, a central question has been whether abstract surfaces with given geometric features can be realized as surfaces in Euclidean space. -

Open Research Online Oro.Open.Ac.Uk
Open Research Online The Open University’s repository of research publications and other research outputs Approaches to the four colour theorem Thesis How to cite: Loupekine, Feodor (1995). Approaches to the four colour theorem. PhD thesis The Open University. For guidance on citations see FAQs. c 1992 The Author https://creativecommons.org/licenses/by-nc-nd/4.0/ Version: Version of Record Link(s) to article on publisher’s website: http://dx.doi.org/doi:10.21954/ou.ro.0000e032 Copyright and Moral Rights for the articles on this site are retained by the individual authors and/or other copyright owners. For more information on Open Research Online’s data policy on reuse of materials please consult the policies page. oro.open.ac.uk ýý ý-ýs-Týý+ý--r Feodor Loupekine, B. Sc. Approaches to the Four Colour Theorem A Thesis Submitted for the Degree of Doctor of Philosophy Faculty of Mathematics The Open University October 1992 Z5 1-1015 .Gý oý awa. pt-LL APPROACHESTO THE FOUR COLOUR THEOREM CONTENTS Page I..... CHAPTER ONE. Introduction Page 6..... CHAPTER TWO. Labelling With Elements of Finite Groups and Fields Page 24.... CHAPTER THREE. Snarks Page 36.... CHAPTER FOUR. Heawood's Theorem and Its Extension to Angles Page 47.... CHAPTERFIVE. The Symmetry Group of the Triangle Page 45.... CHAPTER SIX. Kleinian Colourings in Kleinian Graphs Page 67.... CHAPTERSEVEN. Odd Cut Samples, Odd Cycle Samples Page 73.... CHAPTER EIGHT. Alternate Angle Labelling Page 80.... GLOSSARY. Page 87.... REFERENCES. Page 91.... APPENDIX. "Loupekine's Sharks" by Rufus Isaacs. -i- CHAPTER ONE Introduction In attempting to prove or disprove the notion that all planar maps are Guthrie colourable (i.