Research Article Construction and Analysis of Double Helix for Triangular Bipyramid and Pentangular Bipyramid
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Hexagonal Antiprism Tetragonal Bipyramid Dodecahedron
Call List hexagonal antiprism tetragonal bipyramid dodecahedron hemisphere icosahedron cube triangular bipyramid sphere octahedron cone triangular prism pentagonal bipyramid torus cylinder squarebased pyramid octagonal prism cuboid hexagonal prism pentagonal prism tetrahedron cube octahedron square antiprism ellipsoid pentagonal antiprism spheroid Created using www.BingoCardPrinter.com B I N G O hexagonal triangular squarebased tetrahedron antiprism cube prism pyramid tetragonal triangular pentagonal octagonal cube bipyramid bipyramid bipyramid prism octahedron Free square dodecahedron sphere Space cuboid antiprism hexagonal hemisphere octahedron torus prism ellipsoid pentagonal pentagonal icosahedron cone cylinder prism antiprism Created using www.BingoCardPrinter.com B I N G O triangular pentagonal triangular hemisphere cube prism antiprism bipyramid pentagonal hexagonal tetragonal torus bipyramid prism bipyramid cone square Free hexagonal octagonal tetrahedron antiprism Space antiprism prism squarebased dodecahedron ellipsoid cylinder octahedron pyramid pentagonal icosahedron sphere prism cuboid spheroid Created using www.BingoCardPrinter.com B I N G O cube hexagonal triangular icosahedron octahedron prism torus prism octagonal square dodecahedron hemisphere spheroid prism antiprism Free pentagonal octahedron squarebased pyramid Space cube antiprism hexagonal pentagonal triangular cone antiprism cuboid bipyramid bipyramid tetragonal cylinder tetrahedron ellipsoid bipyramid sphere Created using www.BingoCardPrinter.com B I N G O -
![Crystal Chemical Relations in the Shchurovskyite Family: Synthesis and Crystal Structures of K2cu[Cu3o]2(PO4)4 and K2.35Cu0.825[Cu3o]2(PO4)4](https://docslib.b-cdn.net/cover/6111/crystal-chemical-relations-in-the-shchurovskyite-family-synthesis-and-crystal-structures-of-k2cu-cu3o-2-po4-4-and-k2-35cu0-825-cu3o-2-po4-4-1546111.webp)
Crystal Chemical Relations in the Shchurovskyite Family: Synthesis and Crystal Structures of K2cu[Cu3o]2(PO4)4 and K2.35Cu0.825[Cu3o]2(PO4)4
crystals Article Crystal Chemical Relations in the Shchurovskyite Family: Synthesis and Crystal Structures of K2Cu[Cu3O]2(PO4)4 and K2.35Cu0.825[Cu3O]2(PO4)4 Ilya V. Kornyakov 1,2 and Sergey V. Krivovichev 1,3,* 1 Department of Crystallography, Institute of Earth Sciences, St. Petersburg State University, University Emb. 7/9, 199034 Saint-Petersburg, Russia; [email protected] 2 Laboratory of Nature-Inspired Technologies and Environmental Safety of the Arctic, Kola Science Centre, Russian Academy of Science, Fesmana 14, 184209 Apatity, Russia 3 Nanomaterials Research Center, Federal Research Center–Kola Science Center, Russian Academy of Sciences, Fersmana Str. 14, 184209 Apatity, Russia * Correspondence: [email protected] Abstract: Single crystals of two novel shchurovskyite-related compounds, K2Cu[Cu3O]2(PO4)4 (1) and K2.35Cu0.825[Cu3O]2(PO4)4 (2), were synthesized by crystallization from gaseous phase and structurally characterized using single-crystal X-ray diffraction analysis. The crystal structures of both compounds are based upon similar Cu-based layers, formed by rods of the [O2Cu6] dimers of oxocentered (OCu4) tetrahedra. The topologies of the layers show both similarities and differences from the shchurovskyite-type layers. The layers are connected in different fashions via additional Cu atoms located in the interlayer, in contrast to shchurovskyite, where the layers are linked by Ca2+ cations. The structures of the shchurovskyite family are characterized using information-based Citation: Kornyakov, I.V.; structural complexity measures, which demonstrate that the crystal structure of 1 is the simplest one, Krivovichev, S.V. Crystal Chemical whereas that of 2 is the most complex in the family. -

Volume 75 (2019)
Acta Cryst. (2019). B75, doi:10.1107/S2052520619010047 Supporting information Volume 75 (2019) Supporting information for article: Lanthanide coordination polymers based on designed bifunctional 2-(2,2′:6′,2″-terpyridin-4′-yl)benzenesulfonate ligand: syntheses, structural diversity and highly tunable emission Yi-Chen Hu, Chao Bai, Huai-Ming Hu, Chuan-Ti Li, Tian-Hua Zhang and Weisheng Liu Acta Cryst. (2019). B75, doi:10.1107/S2052520619010047 Supporting information, sup-1 Table S1 Continuous Shape Measures (CShMs) of the coordination geometry for Eu3+ ions in 1- Eu. Label Symmetry Shape 1-Eu EP-9 D9h Enneagon 33.439 OPY-9 C8v Octagonal pyramid 22.561 HBPY-9 D7h Heptagonal bipyramid 15.666 JTC-9 C3v Johnson triangular cupola J3 15.263 JCCU-9 C4v Capped cube J8 10.053 CCU-9 C4v Spherical-relaxed capped cube 9.010 JCSAPR-9 C4v Capped square antiprism J10 2.787 CSAPR-9 C4v Spherical capped square antiprism 1.930 JTCTPR-9 D3h Tricapped trigonal prism J51 3.621 TCTPR-9 D3h Spherical tricapped trigonal prism 2.612 JTDIC-9 C3v Tridiminished icosahedron J63 12.541 HH-9 C2v Hula-hoop 9.076 MFF-9 Cs Muffin 1.659 Acta Cryst. (2019). B75, doi:10.1107/S2052520619010047 Supporting information, sup-2 Table S2 Continuous Shape Measures (CShMs) of the coordination geometry for Ln3+ ions in 2- Er, 4-Tb, and 6-Eu. Label Symmetry Shape 2-Er 4-Tb 6-Eu Er1 Er2 OP-8 D8h Octagon 31.606 31.785 32.793 31.386 HPY-8 C7v Heptagonal pyramid 23.708 24.442 23.407 23.932 HBPY-8 D6h Hexagonal bipyramid 17.013 13.083 12.757 15.881 CU-8 Oh Cube 11.278 11.664 8.749 11.848 -

How Many Times Can the Volume of a Convex Polyhedron Be Increased By
How many times can the volume of a convex polyhedron be increased by isometric deformations? Victor Alexandrov March 1, 2017 Abstract We prove that the answer to the question of the title is ‘as many times as you want.’ More precisely, given any constant c> 0, we construct two oblique triangular bipyramids, P and Q, such that P is convex, Q is nonconvex and intrinsically isometric to P , and vol Q > c·vol P > 0. Mathematics Subject Classification (2010): 52B10; 51M20; 52A15; 52B60; 52C25; 49Q10 Key words: Euclidean space, convex polyhedron, bipyramid, intrinsic metric, intrinsic isome- try, volume increasing deformation 1. Introduction. According to the classical theorem by A.L. Cauchy and A.D. Alexandrov, two compact boundary-free convex polyhedral surfaces in Euclidean 3-space are necessarily con- gruent as soon as they are isometric in their intrinsic metrics, see, e. g., [1]. Obviously, this is not true if at least one of the surfaces is nonconvex. In [4], the authors studied isometric immersions of polyhedral surfaces and, among other things, proved that there exists a compact boundary-free convex polyhedral surface allowing another isometric immersion which, being a nonconvex poly- hedral surface, encloses a larger volume than that enclosed by the original convex surface. This amazing existence theorem has gained new significance after the remarkable contribution of D.D. Bleecker, who explicitly built volume increasing isometric deformations of the surfaces of the Pla- tonic solids, see [3]. For example, he has shown that the surface of a regular tetrahedron can be isometrically deformed in such a way as to enlarge the enclosed volume by 37.7%. -

Unit Origami: Star-Building on Deltahedra Heidi Burgiel Bridgewater State University, [email protected]
Bridgewater State University Virtual Commons - Bridgewater State University Mathematics Faculty Publications Mathematics Department 2015 Unit Origami: Star-Building on Deltahedra Heidi Burgiel Bridgewater State University, [email protected] Virtual Commons Citation Burgiel, Heidi (2015). Unit Origami: Star-Building on Deltahedra. In Mathematics Faculty Publications. Paper 47. Available at: http://vc.bridgew.edu/math_fac/47 This item is available as part of Virtual Commons, the open-access institutional repository of Bridgewater State University, Bridgewater, Massachusetts. Proceedings of Bridges 2015: Mathematics, Music, Art, Architecture, Culture Unit Origami: Star-Building on Deltahedra Heidi Burgiel Dept. of Mathematics, Bridgewater State University 24 Park Avenue, Bridgewater, MA 02325, USA [email protected] Abstract This workshop provides instructions for folding the star-building unit – a modification of the Sonobe module for unit origami. Geometric questions naturally arise during this process, ranging in difficulty from middle school to graduate levels. Participants will learn to fold and assemble star-building units, then explore the structure of the eight strictly convex deltahedra. Introduction Many authors and educators have used origami, the art of paper folding, to provide concrete examples moti- vating mathematical problem solving. [3, 2] In unit origami, multiple sheets are folded and combined to form a whole; the Sonobe unit is a classic module in this art form. This workshop describes the construction and assembly of the star-building unit1, highlights a small selection of the many geometric questions motivated by this process, and introduces participants to the strictly convex deltahedra. Proficiency in geometry and origami is not required to enjoy this event. About the Unit Three Sonobe units interlock to form a pyramid with an equilateral triangular base as shown in Figure 1. -

Supporting Information
Supporting Information Exploring the Slow Magnetic Relaxation of a Family of Photoluminescent 3D Lanthanide-Organic Frameworks Based on Dicarboxylate Ligands Itziar Oyarzabal, Sara Rojas, Ana D. Parejo, Alfonso Salinas-Castillo, José Ángel García, José M. Seco, Javier Cepeda and Antonio Rodríguez-Diéguez Index: 1. Powder X-ray Diffraction 2. Additional structural data 3. Interpretation of void content from SQUEEZE analysis 4. Continuous Shape Measures Calculations 5. Magnetic Properties 6. Luminescence Properties 1 S1. Powder X-ray Diffraction Table S1. Data of pattern-matching refinement of compound 2. Space group P-1 a (Å) 10.87(2) b(Å) 11.11(2) c(Å) 13.26(3) α (°) 105.28(2) β (°) 94.22(3) γ (°) 93.65(2) V/ Å3 1534(3) Figure S1. Pattern-matching analysis and crystalline parameters of the polycrystalline sample of compound 2. Table S2. Data of pattern-matching refinement of compound 3. Space group P-1 a (Å) 10.85(2) b(Å) 11.04(4) c(Å) 13.21(2) α (°) 105.01(2) β (°) 94.90(4) γ (°) 93.90(4) V/ Å3 1516(5) Figure S2. Pattern-matching analysis and crystalline parameters of the polycrystalline sample of compound 3. 2 Table S3. Data of pattern-matching refinement of compound 4. Space group P-1 a (Å) 10.86(2) b(Å) 11.03(4) c(Å) 13.20(2) α (°) 105.20(2) β (°) 94.38(4) γ (°) 93.75(4) V/ Å3 1515(5) Figure S3. Pattern-matching analysis and crystalline parameters of the polycrystalline sample of compound 4. 3 S2. -

Exploring Deltahedra in the Primary Classroom
Exploring deltahedra in the primary classroom Tandi Clausen-May shares some interesting discoveries that children have made exploring shapes made with triangles in her mathematics workshops. s the guiding principles of the ATM state, “The So now I encourage everyone in the workshops to ability to operate mathematically is an aspect look for the nets of both the Regular and the Boat A of human functioning which is as universal octahedra. We display them separately, stopping to as language itself.” So operating mathematically is at think about it if we find the same net in both categories. the heart of the mathematics enrichment workshops The Regular octahedron has only eleven nets, and that I run in primary schools. It is not the specific images of these are readily available in books or on content of the activities that matters: it is the process the internet. Seven of the Regular octahedron nets of exploring new ideas and discovering things are doubles like the one that Josh and Len found: that we did not know. And, just occasionally, quite they can fold up into either of the two delta-octahedra unexpectedly, we discover something that perhaps (Figure 2). not many other people know yet either. That can be incredibly exciting, for all of us. Using squares to make a net that will fold up into a cube is a standard classroom activity for primary school children. Triangle-faced 3-D shapes, or ‘deltahedra’, on the other hand, are less familiar, so they can offer an exciting and engaging new challenge. As we explore the deltahedra and their nets with ATM MATs and Polydron equilateral triangles we work together as a community of mathematicians, Figure 2: The seven nets that will form both the operating mathematically, to move our knowledge Regular and the Boat octahedra. -

Construction and Analysis of Double Helix for Triangular Bipyramid and Pentangular Bipyramid
Hindawi Computational and Mathematical Methods in Medicine Volume 2020, Article ID 5609593, 9 pages https://doi.org/10.1155/2020/5609593 Research Article Construction and Analysis of Double Helix for Triangular Bipyramid and Pentangular Bipyramid Tao Deng 1,2,3 1Key Laboratory of China’s Ethnic Languages and Information Technology of Ministry of Education, Northwest Minzu University, Lanzhou 730030, China 2Key Laboratory of Streaming Data Computing Technologies and Application, Northwest Minzu University, Lanzhou 730030, China 3School of Mathematics and Computer Science, Northwest Minzu University, Lanzhou 730030, China Correspondence should be addressed to Tao Deng; [email protected] Received 20 December 2019; Revised 8 February 2020; Accepted 14 February 2020; Published 14 May 2020 Academic Editor: Nadia A. Chuzhanova Copyright © 2020 Tao Deng. (is is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. DNA cages can be joined together to make larger 3D nanostructures on which molecular electronic circuits and tiny containers are built for drug delivery. (e mathematical models for these promising nanomaterials play important roles in clarifying their assembly mechanism and understanding their structures. In this study, we propose a mathematical and computer method to construct permissible topological structures with double-helical edges for a triangular bipyramid and pentangular bipyramid. Furthermore, we remove the same topological links, without eliminating the nonrepeated ones for a triangular bipyramid and pentangular bipyramid. By analyzing characteristics of these unique links, some self-assembly and statistic rules are discussed. (is study may obtain some new insights into the DNA assembly from the viewpoint of mathematics, promoting the com- prehending and design efficiency of DNA polyhedra with required topological structures. -

Study on Delaunay Tessellations of 1-Irregular Cuboids for 3D Mixed Element Meshes
Study on Delaunay tessellations of 1-irregular cuboids for 3D mixed element meshes David Contreras and Nancy Hitschfeld-Kahler Department of Computer Science, FCFM, University of Chile, Chile E-mails: dcontrer,[email protected] Abstract Mixed elements meshes based on the modified octree approach con- tain several co-spherical point configurations. While generating Delaunay tessellations to be used together with the finite volume method, it is not necessary to partition them into tetrahedra; co-spherical elements can be used as final elements. This paper presents a study of all co-spherical elements that appear while tessellating a 1-irregular cuboid (cuboid with at most one Steiner point on its edges) with different aspect ratio. Steiner points can be located at any position between the edge endpoints. When Steiner points are located at edge midpoints, 24 co-spherical elements appear while tessellating 1-irregular cubes. By inserting internal faces and edges to these new elements, this numberp is reduced to 13. When 1-irregular cuboids with aspect ratio equal to 2 are tessellated, 10 co- spherical elementsp are required. If 1-irregular cuboids have aspect ratio between 1 and 2, all the tessellations are adequate for the finite volume method. When Steiner points are located at any position, the study was done for a specific Steiner point distribution on a cube. 38 co-spherical elements were required to tessellate all the generated 1-irregular cubes. Statistics about the impact of each new element in the tessellations of 1-irregular cuboids are also included. This study was done by develop- ing an algorithm that construct Delaunay tessellations by starting from a Delaunay tetrahedral mesh built by Qhull. -

3.3 Convex Polyhedron
UCC Library and UCC researchers have made this item openly available. Please let us know how this has helped you. Thanks! Title Statistical methods for polyhedral shape classification with incomplete data - application to cryo-electron tomographic images Author(s) Bag, Sukantadev Publication date 2015 Original citation Bag, S. 2015. Statistical methods for polyhedral shape classification with incomplete data - application to cryo-electron tomographic images. PhD Thesis, University College Cork. Type of publication Doctoral thesis Rights © 2015, Sukantadev Bag. http://creativecommons.org/licenses/by-nc-nd/3.0/ Embargo information No embargo required Item downloaded http://hdl.handle.net/10468/2854 from Downloaded on 2021-10-04T09:40:50Z Statistical Methods for Polyhedral Shape Classification with Incomplete Data Application to Cryo-electron Tomographic Images A thesis submitted for the degree of Doctor of Philosophy Sukantadev Bag Department of Statistics College of Science, Engineering and Food Science National University of Ireland, Cork Supervisor: Dr. Kingshuk Roy Choudhury Co-supervisor: Prof. Finbarr O'Sullivan Head of the Department: Dr. Michael Cronin May 2015 IVATIONAL UNIVERSITY OF IRELAIYT}, CORK I)ate: May 2015 Author: Sukantadev Bag Title: Statistical Methods for Polyhedral Shape Classification with Incomplete Data - Application to Cryo-electron Tomographic Images Department: Statistics Degree: Ph. D. Convocation: June 2015 I, Sukantadev Bag ce*iff that this thesis is my own work and I have not obtained a degee in this rmiversity or elsewhere on the basis of the work submitted in this thesis. .. S**ka*h*&.u .....@,,.,. [Signature of Au(}ror] T}IE AI,ITHOR RESERVES OT}IER PUBLICATION RTGHTS, AND NEITIIER THE THESIS NOR EXTENSTVE EXTRACTS FROM IT MAY BE PRINTED OR OTHER- WISE REPRODUCED WTT-HOI.TT TI{E AUTHOR'S WRITTEN PERMISSION. -
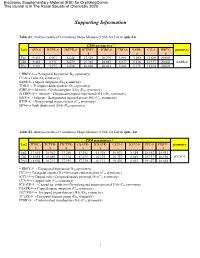
Supporting Information
Electronic Supplementary Material (ESI) for CrystEngComm. This journal is © The Royal Society of Chemistry 2020 Supporting Information Table S1. Analysis results of Continuous Shape Measure (CSM) for Ln1 in cpdc-Ln CSM parameters * Ln1 JSD-8 BTPR-8 JBTPR-8 JETBPY- JGBF-8 TDD-8 SAPR- CU-8 HBPY- geometry 8 8 8 Eu1 9.453 6.003 6.644 27.526 20.710 5.891 5.282 13.610 20.003 Tb1 9.481 5.931 6.679 27.383 20.647 5.837 5.256 13.577 20.001 SAPR-8 Dy1 9.321 5.975 6.534 26.808 20.412 5.841 5.179 13.514 20.023 * HBPY-8→ Hexagonal bipyramid (D6h symmetry) CU-8→ Cube (Oh symmetry) SAPR-8→ Square antiprism (D4d symmetry) TDD-8→ Triangular dodecahedron (D2d symmetry) JGBF-8→ Johnson - Gyrobifastigium (J26) (D2d symmetry) JETBPY-8→ Johnson - Elongated triangular bipyramid (J14) (D3h symmetry) JBTP-8→ Johnson - Biaugmented trigonal prism (J50) (C2v symmetry) BTPR-8→ Biaugmented trigonal prism (C2v symmetry) JSD-8→ Snub disphenoid (J84) (D2d symmetry) Table S2. Analysis results of Continuous Shape Measure (CSM) for Ln2 in cpdc- Ln CSM parameters * Ln2 JTDIC- TCTPR- JTCTPR- CSAPR- JCSAPR- CCU-9 JCCU-9 JTC-9 HBPY- geometry 9 9 9 9 9 9 Eu2 17.653 18.362 17.250 17.382 15.938 10.071 8.314 18.552 18.091 Tb2 18.055 18.685 17.314 17.693 16.135 10.357 8.469 18.937 18.196 JCCU-9 Dy2 18.602 18.713 17.193 17.730 16.131 10.403 8.465 19.327 18.014 * HBPY-9→ Heptagonal bipyramid (D7h symmetry) JTC-9→ Triangular cupola (J3) = trivacant cuboctahedron (C3v symmetry) JCCU-9→ Capped cube (Elongated square pyramid, J8) (C4v symmetry) CCU-9→ Capped cube (C4v symmetry) JCSAPR-9→ Capped sq. -

DIPLOMOVÁ PRÁCE Polopravidelné Rovinné Grafy
UNIVERZITA PALACKÉHO V OLOMOUCI PŘÍRODOVĚDECKÁ FAKULTA KATEDRA ALGEBRY A GEOMETRIE DIPLOMOVÁ PRÁCE Polopravidelné rovinné grafy Vedoucí diplomové práce: Vypracovala: RNDr. Zdeněk Dušek, Ph.D. Bc. Jitka Doležalová Rok odevzdání: 2010 Diskrétní matematika, 5. ročník Prohlášení Prohlašuji, že jsem vypracovala tuto diplomovou práci samostatně, a že jsem v seznamu použité literatury uvedla všechny zdroje použité při zpracování práce. V Olomouci dne 23. dubna 2010 Poděkování Ráda bych na tomto místě poděkovala RNDr. Zdeňku Duškovi, Ph.D., za obětavou spolu- práci i za čas, který mi věnoval při konzultacích. Obsah Úvod 2 1 Rovinné grafy 4 2 Konvexní mnohostěny 9 3 Pravidelné rovinné grafy a mnohostěny 11 4 Speciální polopravidelné rovinné grafy 13 4.1 Archimedovská tělesa, hranoly a antihranoly . ........ 13 4.2 Johnsonovatělesa................................ 22 4.3 Zobecněnéhranolyaantihranoly . ... 25 5 Polopravidelné rovinné grafy se stejnými vrcholy 26 6 Polopravidelné rovinné grafy se stejnými stěnami 41 6.1 Katalánskátělesa ................................ 41 6.2 Duální grafy ke grafům Johnsonových těles . ...... 44 6.3 Duální grafy ke grafům zobecněných hranolů a antihranolů......... 45 6.4 Duální grafy k obecným polopravidelným grafům . ...... 46 Literatura 56 Příloha - přehled Johnsonových těles 58 1 Úvod Dokonalost pravidelných mnohostěnů přitahovala lidskou pozornost již od dob antického Řecka. Jeden z nejvýznamnějších řeckých filozofů - Platon (427 př. n. l. 347 př. n. l.) v nich spatřoval podstatu struktury Vesmíru. Krychli, osmistěn, čtyřstěn a dvacetistěn považoval za představitele čtyř základních živlů, jimiž byly podle jeho učení země, vzduch, oheň a voda, a dvanáctistěn za představitele jsoucna. O matematický popis platonských těles se jako první pokusil Thaeten z Athén (417 př. n. l. - 369 př.