DOCSLIB.ORG

Modern Methods of Quantum Chromodynamics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Modern Methods of Quantum Chromodynamics Modern Methods of Quantum Chromodynamics Christian Schwinn Albert-Ludwigs-Universit¨atFreiburg, Physikalisches Institut D-79104 Freiburg, Germany Winter-Semester 2014/15 Draft: March 30, 2015 http://www.tep.physik.uni-freiburg.de/lectures/QCD-WS-14 2 Contents 1 Introduction 9 Hadrons and quarks . .9 QFT and QED . .9 QCD: theory of quarks and gluons . .9 QCD and LHC physics . 10 Multi-parton scattering amplitudes . 10 NLO calculations . 11 Remarks on the lecture . 11 I Parton Model and QCD 13 2 Quarks and colour 15 2.1 Hadrons and quarks . 15 Hadrons and the strong interactions . 15 Quark Model . 15 2.2 Parton Model . 16 Deep inelastic scattering . 16 Parton distribution functions . 18 2.3 Colour degree of freedom . 19 Postulate of colour quantum number . 19 Colour-SU(3).............................. 20 Confinement . 20 Evidence of colour: e+e− ! hadrons . 21 2.4 Towards QCD . 22 3 Basics of QFT and QED 25 3.1 Quantum numbers of relativistic particles . 25 3.1.1 Poincar´egroup . 26 3.1.2 Relativistic one-particle states . 27 3.2 Quantum fields . 32 3.2.1 Scalar fields . 32 3.2.2 Spinor fields . 32 3 4 CONTENTS Dirac spinors . 33 Massless spin one-half particles . 34 Spinor products . 35 Quantization . 35 3.2.3 Massless vector bosons . 35 Polarization vectors and gauge invariance . 36 3.3 QED . 37 3.4 Feynman rules . 39 3.4.1 S-matrix and Cross section . 39 S-matrix . 39 Poincar´einvariance of the S-matrix . 40 T -matrix and scattering amplitude . 41 Unitarity of the S-matrix . 41 Cross section . 42 3.4.2 Perturbation theory and Feynman rules . 42 Feynman rules . 43 3.4.3 Feynman rules in QED . 44 3.4.4 Feynman rules for interactions with momenta . 45 3.5 Calculation of cross sections . 46 3.5.1 Example: e−e+ ! µ−µ+ ........................ 46 3.5.2 Remarks on the calculation of scattering amplitudes . 48 Crossing: e−µ ! e−µ .......................... 48 External photons and gauge invariance . 49 Remarks on calculations for many-particle final states . 50 4 Introduction to QCD 51 4.1 SU(3) ...................................... 52 4.1.1 Generators and Lie Algebra . 52 Lie Groups and generators . 52 Gell-Mann matrices . 53 Lie Algebras . 53 4.1.2 Representations . 54 Fundamental representations . 54 Combining representations . 55 Representations of Lie algebras . 57 Conjugate representation . 57 Adjoint representation . 57 Generators of product representations . 58 4.2 QCD as non-abelian gauge theory . 58 4.2.1 Non-abelian gauge invariance . 58 Covariant derivative . 58 Field-strength tensor . 59 Decomposition of gluon fields . 59 CONTENTS 5 Infinitesimal transformations . 60 4.2.2 QCD Lagrangian . 60 4.2.3 Gauge fixing . 61 4.3 Feynman rules . 62 4.4 Evaluation of colour factors . 64 Casimir operators . 64 Colour Fierz identity . 66 4.5 Examples . 66 4.5.1 Quark-antiquark potential . 66 4.5.2 qq¯ ! gg: Gauge invariance and ghosts . 68 Ward identity . 69 Relation to ghost diagrams . 70 5 Applications of the Parton model 73 5.1 e−e+ ! Hadrons . 74 5.1.1 Electromagnetic quark current . 74 5.1.2 Total cross section . 74 5.2 DIS . 77 DIS cross section in the naive parton model . 77 Field-theoretic treatment . 79 Derivation of the cross section . 80 5.3 The Drell-Yan process . 81 5.4 Dijet cross sections . 83 5.4.1 Four-quark processes . 84 II Multi-leg Born amplitudes 87 6 Spinor-helicity methods 89 6.1 Two-component spinors . 89 6.1.1 Weyl Spinors . 89 Lorentz Transformations . 89 6.1.2 Index notation . 90 Raising and lowering indices . 90 Spinor products . 91 Explicit expressions . 91 Conjugate spinors . 92 Dirac spinors . 92 Schouten Identity . 93 Braket notation . 93 6.2 Momenta and spinors . 93 6.2.1 Pauli matrices . 93 Raising and lowering indices . 94 6 CONTENTS Dirac algebra . 94 Fierz identities . 94 6.2.2 Four-momenta . 95 Factorization of momenta into spinors . 95 Constructing momenta from spinors . 95 Scaling . 96 6.2.3 Gluon polarization vectors . 96 6.2.4 Rules for calculations with Weyl spinors . 97 Properties of spinor products . 97 Momentum conservation . 97 External states . 98 6.3 Examples . 98 6.3.1 e−e+ ! qq¯ ................................ 99 6.3.2 e−e+ ! qqg¯ ............................... 100 7 Colour decomposition 103 7.1 Examples . 104 7.1.1 qq¯ ! gg ................................. 104 7.1.2 gg ! gg ................................. 105 7.2 Colour ordered Feynman rules . 106 7.2.1 Colour ordered vertices . 106 Three gluon vertex . 106 Four gluon vertex . 106 7.2.2 Colour ordered multi-gluon amplitudes . 106 8 Born amplitudes 109 8.1 General considerations . ..
Load more

Recommended publications
  • QCD Theory 6Em2pt Formation of Quark-Gluon Plasma In
    QCD theory Formation of quark-gluon plasma in QCD T. Lappi University of Jyvaskyl¨ a,¨ Finland Particle physics day, Helsinki, October 2017 1/16 Outline I Heavy ion collision: big picture I Initial state: small-x gluons I Production of particles in weak coupling: gluon saturation I 2 ways of understanding glue I Counting particles I Measuring gluon field I For practical phenomenology: add geometry 2/16 A heavy ion event at the LHC How does one understand what happened here? 3/16 Concentrate here on the earliest stage Heavy ion collision in spacetime The purpose in heavy ion collisions: to create QCD matter, i.e. system that is large and lives long compared to the microscopic scale 1 1 t L T > 200MeV T T t freezefreezeout out hadronshadron in eq. gas gluonsquark-gluon & quarks in eq. plasma gluonsnonequilibrium & quarks out of eq. quarks, gluons colorstrong fields fields z (beam axis) 4/16 Heavy ion collision in spacetime The purpose in heavy ion collisions: to create QCD matter, i.e. system that is large and lives long compared to the microscopic scale 1 1 t L T > 200MeV T T t freezefreezeout out hadronshadron in eq. gas gluonsquark-gluon & quarks in eq. plasma gluonsnonequilibrium & quarks out of eq. quarks, gluons colorstrong fields fields z (beam axis) Concentrate here on the earliest stage 4/16 Color charge I Charge has cloud of gluons I But now: gluons are source of new gluons: cascade dN !−1−O(αs) d! ∼ Cascade of gluons Electric charge I At rest: Coulomb electric field I Moving at high velocity: Coulomb field is cloud of photons
    [Show full text]
  • The Positons of the Three Quarks Composing the Proton Are Illustrated
    The posi1ons of the three quarks composing the proton are illustrated by the colored spheres. The surface plot illustrates the reduc1on of the vacuum ac1on density in a plane passing through the centers of the quarks. The vector field illustrates the gradient of this reduc1on. The posi1ons in space where the vacuum ac1on is maximally expelled from the interior of the proton are also illustrated by the tube-like structures, exposing the presence of flux tubes. a key point of interest is the distance at which the flux-tube formaon occurs. The animaon indicates that the transi1on to flux-tube formaon occurs when the distance of the quarks from the center of the triangle is greater than 0.5 fm. again, the diameter of the flux tubes remains approximately constant as the quarks move to large separaons. • Three quarks indicated by red, green and blue spheres (lower leb) are localized by the gluon field. • a quark-an1quark pair created from the gluon field is illustrated by the green-an1green (magenta) quark pair on the right. These quark pairs give rise to a meson cloud around the proton. hEp://www.physics.adelaide.edu.au/theory/staff/leinweber/VisualQCD/Nobel/index.html Nucl. Phys. A750, 84 (2005) 1000000 QCD mass 100000 Higgs mass 10000 1000 100 Mass (MeV) 10 1 u d s c b t GeV HOW does the rest of the proton mass arise? HOW does the rest of the proton spin (magnetic moment,…), arise? Mass from nothing Dyson-Schwinger and Lattice QCD It is known that the dynamical chiral symmetry breaking; namely, the generation of mass from nothing, does take place in QCD.
    [Show full text]
  • Quantum Mechanics Quantum Chromodynamics (QCD)
    Quantum Mechanics_quantum chromodynamics (QCD) In theoretical physics, quantum chromodynamics (QCD) is a theory ofstrong interactions, a fundamental forcedescribing the interactions between quarksand gluons which make up hadrons such as the proton, neutron and pion. QCD is a type of Quantum field theory called a non- abelian gauge theory with symmetry group SU(3). The QCD analog of electric charge is a property called 'color'. Gluons are the force carrier of the theory, like photons are for the electromagnetic force in quantum electrodynamics. The theory is an important part of the Standard Model of Particle physics. A huge body of experimental evidence for QCD has been gathered over the years. QCD enjoys two peculiar properties: Confinement, which means that the force between quarks does not diminish as they are separated. Because of this, when you do split the quark the energy is enough to create another quark thus creating another quark pair; they are forever bound into hadrons such as theproton and the neutron or the pion and kaon. Although analytically unproven, confinement is widely believed to be true because it explains the consistent failure of free quark searches, and it is easy to demonstrate in lattice QCD. Asymptotic freedom, which means that in very high-energy reactions, quarks and gluons interact very weakly creating a quark–gluon plasma. This prediction of QCD was first discovered in the early 1970s by David Politzer and by Frank Wilczek and David Gross. For this work they were awarded the 2004 Nobel Prize in Physics. There is no known phase-transition line separating these two properties; confinement is dominant in low-energy scales but, as energy increases, asymptotic freedom becomes dominant.
    [Show full text]
  • PDF) of Partons I and J
    TASI 2004 Lecture Notes on Higgs Boson Physics∗ Laura Reina1 1Physics Department, Florida State University, 315 Keen Building, Tallahassee, FL 32306-4350, USA E-mail: [email protected] Abstract In these lectures I briefly review the Higgs mechanism of spontaneous symmetry breaking and focus on the most relevant aspects of the phenomenology of the Standard Model and of the Minimal Supersymmetric Standard Model Higgs bosons at both hadron (Tevatron, Large Hadron Collider) and lepton (International Linear Collider) colliders. Some emphasis is put on the perturbative calculation of both Higgs boson branching ratios and production cross sections, including the most important radiative corrections. arXiv:hep-ph/0512377v1 30 Dec 2005 ∗ These lectures are dedicated to Filippo, who listened to them before he was born and behaved really well while I was writing these proceedings. 1 Contents I. Introduction 3 II. Theoretical framework: the Higgs mechanism and its consequences. 4 A. A brief introduction to the Higgs mechanism 5 B. The Higgs sector of the Standard Model 10 C. Theoretical constraints on the Standard Model Higgs bosonmass 13 1. Unitarity 14 2. Triviality and vacuum stability 16 3. Indirect bounds from electroweak precision measurements 17 4. Fine-tuning 22 D. The Higgs sector of the Minimal Supersymmetric Standard Model 24 1. About Two Higgs Doublet Models 25 2. The MSSM Higgs sector: introduction 27 3. MSSM Higgs boson couplings to electroweak gauge bosons 30 4. MSSM Higgs boson couplings to fermions 33 III. Phenomenology of the Higgs Boson 34 A. Standard Model Higgs boson decay branching ratios 34 1. General properties of radiative corrections to Higgs decays 37 + 2.
    [Show full text]
  • Unitarity Constraints on Higgs Portals
    SLAC-PUB-15822 Unitarity Constraints on Higgs Portals Devin G. E. Walker SLAC National Accelerator Laboratory, 2575 Sand Hill Road, Menlo Park, CA 94025, U.S.A. Dark matter that was once in thermal equilibrium with the Standard Model is generally prohibited from obtaining all of its mass from the electroweak phase transition. This implies a new scale of physics and mediator particles to facilitate dark matter annihilation. In this work, we focus on dark matter that annihilates through a generic Higgs portal. We show how partial wave unitarity places an upper bound on the mass of the mediator (or dark) Higgs when its mass is increased to be the largest scale in the effective theory. For models where the dark matter annihilates via fermion exchange, an upper bound is generated when unitarity breaks down around 8.5 TeV. Models where the dark matter annihilates via fermion and higgs boson exchange push the bound to 45.5 TeV. We also show that if dark matter obtains all of its mass from a new symmetry breaking scale that scale is also constrained. We improve these constraints by requiring perturbativity in the Higgs sector up to each unitarity bound. In this limit, the bounds on the dark symmetry breaking vev and the dark Higgs mass are now 2.4 and 3 TeV, respectively, when the dark matter annihilates via fermion exchange. When dark matter annihilates via fermion and higgs boson exchange, the bounds are now 12 and 14.2 TeV, respectively. Given the unitarity bounds, the available parameter space for Higgs portal dark matter annihilation is outlined.
    [Show full text]
  • The Center Symmetry and Its Spontaneous Breakdown at High Temperatures
    CORE Metadata, citation and similar papers at core.ac.uk Provided by CERN Document Server THE CENTER SYMMETRY AND ITS SPONTANEOUS BREAKDOWN AT HIGH TEMPERATURES KIERAN HOLLAND Institute for Theoretical Physics, University of Bern, CH-3012 Bern, Switzerland UWE-JENS WIESE Center for Theoretical Physics, Laboratory for Nuclear Science and Department of Physics, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA The Euclidean action of non-Abelian gauge theories with adjoint dynamical charges (gluons or gluinos) at non-zero temperature T is invariant against topologically non-trivial gauge transformations in the ZZ(N)c center of the SU(N) gauge group. The Polyakov loop measures the free energy of fundamental static charges (in- finitely heavy test quarks) and is an order parameter for the spontaneous break- down of the center symmetry. In SU(N) Yang-Mills theory the ZZ(N)c symmetry is unbroken in the low-temperature confined phase and spontaneously broken in the high-temperature deconfined phase. In 4-dimensional SU(2) Yang-Mills the- ory the deconfinement phase transition is of second order and is in the universality class of the 3-dimensional Ising model. In the SU(3) theory, on the other hand, the transition is first order and its bulk physics is not universal. When a chemical potential µ is used to generate a non-zero baryon density of test quarks, the first order deconfinement transition line extends into the (µ, T )-plane. It terminates at a critical endpoint which also is in the universality class of the 3-dimensional Ising model. At a first order phase transition the confined and deconfined phases coexist and are separated by confined-deconfined interfaces.
    [Show full text]
  • The Confinement Problem in Lattice Gauge Theory
    The Confinement Problem in Lattice Gauge Theory J. Greensite 1,2 1Physics and Astronomy Department San Francisco State University San Francisco, CA 94132 USA 2Theory Group, Lawrence Berkeley National Laboratory Berkeley, CA 94720 USA February 1, 2008 Abstract I review investigations of the quark confinement mechanism that have been carried out in the framework of SU(N) lattice gauge theory. The special role of ZN center symmetry is emphasized. 1 Introduction When the quark model of hadrons was first introduced by Gell-Mann and Zweig in 1964, an obvious question was “where are the quarks?”. At the time, one could respond that the arXiv:hep-lat/0301023v2 5 Mar 2003 quark model was simply a useful scheme for classifying hadrons, and the notion of quarks as actual particles need not be taken seriously. But the absence of isolated quark states became a much more urgent issue with the successes of the quark-parton model, and the introduction, in 1972, of quantum chromodynamics as a fundamental theory of hadronic physics [1]. It was then necessary to suppose that, somehow or other, the dynamics of the gluon sector of QCD contrives to eliminate free quark states from the spectrum. Today almost no one seriously doubts that quantum chromodynamics confines quarks. Following many theoretical suggestions in the late 1970’s about how quark confinement might come about, it was finally the computer simulations of QCD, initiated by Creutz [2] in 1980, that persuaded most skeptics. Quark confinement is now an old and familiar idea, routinely incorporated into the standard model and all its proposed extensions, and the focus of particle phenomenology shifted long ago to other issues.
    [Show full text]
  • Symmetries in Quantum Field Theory and Quantum Gravity
    Symmetries in Quantum Field Theory and Quantum Gravity Daniel Harlowa and Hirosi Oogurib;c aCenter for Theoretical Physics Massachusetts Institute of Technology, Cambridge, MA 02139, USA bWalter Burke Institute for Theoretical Physics California Institute of Technology, Pasadena, CA 91125, USA cKavli Institute for the Physics and Mathematics of the Universe (WPI) University of Tokyo, Kashiwa, 277-8583, Japan E-mail: [email protected], [email protected] Abstract: In this paper we use the AdS/CFT correspondence to refine and then es- tablish a set of old conjectures about symmetries in quantum gravity. We first show that any global symmetry, discrete or continuous, in a bulk quantum gravity theory with a CFT dual would lead to an inconsistency in that CFT, and thus that there are no bulk global symmetries in AdS/CFT. We then argue that any \long-range" bulk gauge symmetry leads to a global symmetry in the boundary CFT, whose consistency requires the existence of bulk dynamical objects which transform in all finite-dimensional irre- ducible representations of the bulk gauge group. We mostly assume that all internal symmetry groups are compact, but we also give a general condition on CFTs, which we expect to be true quite broadly, which implies this. We extend all of these results to the case of higher-form symmetries. Finally we extend a recently proposed new motivation for the weak gravity conjecture to more general gauge groups, reproducing the \convex hull condition" of Cheung and Remmen. An essential point, which we dwell on at length, is precisely defining what we mean by gauge and global symmetries in the bulk and boundary.
    [Show full text]
  • Phenomenological Review on Quark–Gluon Plasma: Concepts Vs
    Review Phenomenological Review on Quark–Gluon Plasma: Concepts vs. Observations Roman Pasechnik 1,* and Michal Šumbera 2 1 Department of Astronomy and Theoretical Physics, Lund University, SE-223 62 Lund, Sweden 2 Nuclear Physics Institute ASCR 250 68 Rez/Prague,ˇ Czech Republic; [email protected] * Correspondence: [email protected] Abstract: In this review, we present an up-to-date phenomenological summary of research developments in the physics of the Quark–Gluon Plasma (QGP). A short historical perspective and theoretical motivation for this rapidly developing field of contemporary particle physics is provided. In addition, we introduce and discuss the role of the quantum chromodynamics (QCD) ground state, non-perturbative and lattice QCD results on the QGP properties, as well as the transport models used to make a connection between theory and experiment. The experimental part presents the selected results on bulk observables, hard and penetrating probes obtained in the ultra-relativistic heavy-ion experiments carried out at the Brookhaven National Laboratory Relativistic Heavy Ion Collider (BNL RHIC) and CERN Super Proton Synchrotron (SPS) and Large Hadron Collider (LHC) accelerators. We also give a brief overview of new developments related to the ongoing searches of the QCD critical point and to the collectivity in small (p + p and p + A) systems. Keywords: extreme states of matter; heavy ion collisions; QCD critical point; quark–gluon plasma; saturation phenomena; QCD vacuum PACS: 25.75.-q, 12.38.Mh, 25.75.Nq, 21.65.Qr 1. Introduction Quark–gluon plasma (QGP) is a new state of nuclear matter existing at extremely high temperatures and densities when composite states called hadrons (protons, neutrons, pions, etc.) lose their identity and dissolve into a soup of their constituents—quarks and gluons.
    [Show full text]
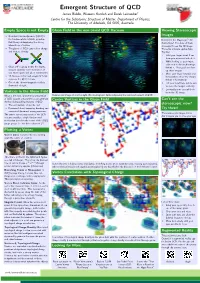
  • Emergent Structure Of
    Emergent Structure of QCD James Biddle, Waseem Kamleh and Derek Leinwebery Centre for the Subatomic Structure of Matter, Department of Physics, The University of Adelaide, SA 5005, Australia Empty Space is not Empty Gluon Field in the non-trivial QCD Vacuum Viewing Stereoscopic Images Quantum Chromodynamics (QCD) is the fundamental relativistic quantum Remember the Magic Eye R 3D field theory underpinning the strong illustrations? You stare at them interactions of nature. cross-eyed to see the 3D image. The gluons of QCD carry colour charge The same principle applies here. and interact directly Try this! 1. Hold your finger about 5 cm from your nose and look at it. 2. While looking at your finger, take note of the double image Gluon self-coupling makes the empty behind it. Your goal is to line vacuum unstable to the formation of up those images. non-trivial quark and gluon condensates. 3. Move your finger forwards and 16 chromo-electric and -magnetic fields backwards to move the images compose the QCD vacuum. behind it horizontally. One of the chromo-magnetic fields is 4. Tilt your head from side to side illustrated at right. to move the images vertically. 5. Eventually your eyes will lock Vortices in the Gluon Field in on the 3D image. What is the most fundamental perspective Stereoscopic image of one the eight chromo-magnetic fields composing the nontrivial vacuum of QCD. of QCD vacuum structure that can generate Centre Vortices in the Gluon Field Can't see the the key distinguishing features of QCD stereoscopic view? The confinement of quarks, and Dynamical chiral symmetry breaking and Try these! associated dynamical-mass generation.
    [Show full text]
  • TASI 2013 Lectures on Higgs Physics Within and Beyond the Standard Model∗
    TASI 2013 lectures on Higgs physics within and beyond the Standard Model∗ Heather E. Logany Ottawa-Carleton Institute for Physics, Carleton University, 1125 Colonel By Drive, Ottawa, Ontario K1S 5B6 Canada June 2014 Abstract These lectures start with a detailed pedagogical introduction to electroweak symmetry breaking in the Standard Model, including gauge boson and fermion mass generation and the resulting predictions for Higgs boson interactions. I then survey Higgs boson decays and production mechanisms at hadron and e+e− colliders. I finish with two case studies of Higgs physics beyond the Standard Model: two- Higgs-doublet models, which I use to illustrate the concept of minimal flavor violation, and models with isospin-triplet scalar(s), which I use to illustrate the concept of custodial symmetry. arXiv:1406.1786v2 [hep-ph] 28 Nov 2017 ∗Comments are welcome and will inform future versions of these lecture notes. I hereby release all the figures in these lectures into the public domain. Share and enjoy! [email protected] 1 Contents 1 Introduction 3 2 The Higgs mechanism in the Standard Model 3 2.1 Preliminaries: gauge sector . .3 2.2 Preliminaries: fermion sector . .4 2.3 The SM Higgs mechanism . .5 2.4 Gauge boson masses and couplings to the Higgs boson . .8 2.5 Fermion masses, the CKM matrix, and couplings to the Higgs boson . 12 2.5.1 Lepton masses . 12 2.5.2 Quark masses and mixing . 13 2.5.3 An aside on neutrino masses . 16 2.5.4 CKM matrix parameter counting . 17 2.6 Higgs self-couplings .
    [Show full text]
  • 2014Fall QFT Final Examination—Hunting for the Higgs
    2014Fall QFT Final Examination|Hunting for the Higgs Yao-Chieh Hu1, ∗ 1Department of Physics, National Taiwan University, Taipei 10617, Taiwan (Dated: January 18, 2015) There are many colliders and experiences now studying the Higgs bosons, like Large Electron- Positron Collider (LEP), the Tevatron, and the Large Hadron Collider (LHC). In this report, we will focus on the experiment at the LHC, where the Higgs was found on 4 July 2012 and be temporarily confirmed on 14 March 2013 with the mass about 125GeV. The production and the detection of the Higgs will be mentioned, and also some future research for new physics at LHC. I. INTRODUCTION Note that the coupling is proportional to the mass of the fermion. After Learning the electroweak interaction, we know The couplings of the Higgs boson to the gauge fields are µ y that the Higgs mechanism provides a general framework through the kinetic term, (D φ) (Dµφ). The covariant to explain the spontaneously symmetry breaking with derivative is ± SU(2) × U(1) to U(1)and give masses to the W and Z gauge bosons. The high energy U(1) symmetry is called a a 1 0 Dµφ = @µ − igAµτ − i g Bµ φ, (5) hypercharge, denoted as U(1)Y ; this U(1)Y should not 2 be confused with the EM gauge symmetry U(1)EM . (In a in which Aµ and Bµ are the gauge bosons of the SU(2) SM, the SU(2) × U(1)Y is broken by the VEV of a com- 0 plex doublet H with hypercharge 1=2 called the Higgs and U(1) groups, respectively, with g and g being the multiplet.) According to what we have learned, we can corresponding coupling constants.
    [Show full text]