The Positons of the Three Quarks Composing the Proton Are Illustrated
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

QCD Theory 6Em2pt Formation of Quark-Gluon Plasma In
QCD theory Formation of quark-gluon plasma in QCD T. Lappi University of Jyvaskyl¨ a,¨ Finland Particle physics day, Helsinki, October 2017 1/16 Outline I Heavy ion collision: big picture I Initial state: small-x gluons I Production of particles in weak coupling: gluon saturation I 2 ways of understanding glue I Counting particles I Measuring gluon field I For practical phenomenology: add geometry 2/16 A heavy ion event at the LHC How does one understand what happened here? 3/16 Concentrate here on the earliest stage Heavy ion collision in spacetime The purpose in heavy ion collisions: to create QCD matter, i.e. system that is large and lives long compared to the microscopic scale 1 1 t L T > 200MeV T T t freezefreezeout out hadronshadron in eq. gas gluonsquark-gluon & quarks in eq. plasma gluonsnonequilibrium & quarks out of eq. quarks, gluons colorstrong fields fields z (beam axis) 4/16 Heavy ion collision in spacetime The purpose in heavy ion collisions: to create QCD matter, i.e. system that is large and lives long compared to the microscopic scale 1 1 t L T > 200MeV T T t freezefreezeout out hadronshadron in eq. gas gluonsquark-gluon & quarks in eq. plasma gluonsnonequilibrium & quarks out of eq. quarks, gluons colorstrong fields fields z (beam axis) Concentrate here on the earliest stage 4/16 Color charge I Charge has cloud of gluons I But now: gluons are source of new gluons: cascade dN !−1−O(αs) d! ∼ Cascade of gluons Electric charge I At rest: Coulomb electric field I Moving at high velocity: Coulomb field is cloud of photons -

First Determination of the Electric Charge of the Top Quark
First Determination of the Electric Charge of the Top Quark PER HANSSON arXiv:hep-ex/0702004v1 1 Feb 2007 Licentiate Thesis Stockholm, Sweden 2006 Licentiate Thesis First Determination of the Electric Charge of the Top Quark Per Hansson Particle and Astroparticle Physics, Department of Physics Royal Institute of Technology, SE-106 91 Stockholm, Sweden Stockholm, Sweden 2006 Cover illustration: View of a top quark pair event with an electron and four jets in the final state. Image by DØ Collaboration. Akademisk avhandling som med tillst˚and av Kungliga Tekniska H¨ogskolan i Stock- holm framl¨agges till offentlig granskning f¨or avl¨aggande av filosofie licentiatexamen fredagen den 24 november 2006 14.00 i sal FB54, AlbaNova Universitets Center, KTH Partikel- och Astropartikelfysik, Roslagstullsbacken 21, Stockholm. Avhandlingen f¨orsvaras p˚aengelska. ISBN 91-7178-493-4 TRITA-FYS 2006:69 ISSN 0280-316X ISRN KTH/FYS/--06:69--SE c Per Hansson, Oct 2006 Printed by Universitetsservice US AB 2006 Abstract In this thesis, the first determination of the electric charge of the top quark is presented using 370 pb−1 of data recorded by the DØ detector at the Fermilab Tevatron accelerator. tt¯ events are selected with one isolated electron or muon and at least four jets out of which two are b-tagged by reconstruction of a secondary decay vertex (SVT). The method is based on the discrimination between b- and ¯b-quark jets using a jet charge algorithm applied to SVT-tagged jets. A method to calibrate the jet charge algorithm with data is developed. A constrained kinematic fit is performed to associate the W bosons to the correct b-quark jets in the event and extract the top quark electric charge. -

Properties of Baryons in the Chiral Quark Model
Properties of Baryons in the Chiral Quark Model Tommy Ohlsson Teknologie licentiatavhandling Kungliga Tekniska Hogskolan¨ Stockholm 1997 Properties of Baryons in the Chiral Quark Model Tommy Ohlsson Licentiate Dissertation Theoretical Physics Department of Physics Royal Institute of Technology Stockholm, Sweden 1997 Typeset in LATEX Akademisk avhandling f¨or teknologie licentiatexamen (TeknL) inom ¨amnesomr˚adet teoretisk fysik. Scientific thesis for the degree of Licentiate of Engineering (Lic Eng) in the subject area of Theoretical Physics. TRITA-FYS-8026 ISSN 0280-316X ISRN KTH/FYS/TEO/R--97/9--SE ISBN 91-7170-211-3 c Tommy Ohlsson 1997 Printed in Sweden by KTH H¨ogskoletryckeriet, Stockholm 1997 Properties of Baryons in the Chiral Quark Model Tommy Ohlsson Teoretisk fysik, Institutionen f¨or fysik, Kungliga Tekniska H¨ogskolan SE-100 44 Stockholm SWEDEN E-mail: [email protected] Abstract In this thesis, several properties of baryons are studied using the chiral quark model. The chiral quark model is a theory which can be used to describe low energy phenomena of baryons. In Paper 1, the chiral quark model is studied using wave functions with configuration mixing. This study is motivated by the fact that the chiral quark model cannot otherwise break the Coleman–Glashow sum-rule for the magnetic moments of the octet baryons, which is experimentally broken by about ten standard deviations. Configuration mixing with quark-diquark components is also able to reproduce the octet baryon magnetic moments very accurately. In Paper 2, the chiral quark model is used to calculate the decuplet baryon ++ magnetic moments. The values for the magnetic moments of the ∆ and Ω− are in good agreement with the experimental results. -

Modern Methods of Quantum Chromodynamics
Modern Methods of Quantum Chromodynamics Christian Schwinn Albert-Ludwigs-Universit¨atFreiburg, Physikalisches Institut D-79104 Freiburg, Germany Winter-Semester 2014/15 Draft: March 30, 2015 http://www.tep.physik.uni-freiburg.de/lectures/QCD-WS-14 2 Contents 1 Introduction 9 Hadrons and quarks . .9 QFT and QED . .9 QCD: theory of quarks and gluons . .9 QCD and LHC physics . 10 Multi-parton scattering amplitudes . 10 NLO calculations . 11 Remarks on the lecture . 11 I Parton Model and QCD 13 2 Quarks and colour 15 2.1 Hadrons and quarks . 15 Hadrons and the strong interactions . 15 Quark Model . 15 2.2 Parton Model . 16 Deep inelastic scattering . 16 Parton distribution functions . 18 2.3 Colour degree of freedom . 19 Postulate of colour quantum number . 19 Colour-SU(3).............................. 20 Confinement . 20 Evidence of colour: e+e− ! hadrons . 21 2.4 Towards QCD . 22 3 Basics of QFT and QED 25 3.1 Quantum numbers of relativistic particles . 25 3.1.1 Poincar´egroup . 26 3.1.2 Relativistic one-particle states . 27 3.2 Quantum fields . 32 3.2.1 Scalar fields . 32 3.2.2 Spinor fields . 32 3 4 CONTENTS Dirac spinors . 33 Massless spin one-half particles . 34 Spinor products . 35 Quantization . 35 3.2.3 Massless vector bosons . 35 Polarization vectors and gauge invariance . 36 3.3 QED . 37 3.4 Feynman rules . 39 3.4.1 S-matrix and Cross section . 39 S-matrix . 39 Poincar´einvariance of the S-matrix . 40 T -matrix and scattering amplitude . 41 Unitarity of the S-matrix . 41 Cross section . -

The Center Symmetry and Its Spontaneous Breakdown at High Temperatures
CORE Metadata, citation and similar papers at core.ac.uk Provided by CERN Document Server THE CENTER SYMMETRY AND ITS SPONTANEOUS BREAKDOWN AT HIGH TEMPERATURES KIERAN HOLLAND Institute for Theoretical Physics, University of Bern, CH-3012 Bern, Switzerland UWE-JENS WIESE Center for Theoretical Physics, Laboratory for Nuclear Science and Department of Physics, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA The Euclidean action of non-Abelian gauge theories with adjoint dynamical charges (gluons or gluinos) at non-zero temperature T is invariant against topologically non-trivial gauge transformations in the ZZ(N)c center of the SU(N) gauge group. The Polyakov loop measures the free energy of fundamental static charges (in- finitely heavy test quarks) and is an order parameter for the spontaneous break- down of the center symmetry. In SU(N) Yang-Mills theory the ZZ(N)c symmetry is unbroken in the low-temperature confined phase and spontaneously broken in the high-temperature deconfined phase. In 4-dimensional SU(2) Yang-Mills the- ory the deconfinement phase transition is of second order and is in the universality class of the 3-dimensional Ising model. In the SU(3) theory, on the other hand, the transition is first order and its bulk physics is not universal. When a chemical potential µ is used to generate a non-zero baryon density of test quarks, the first order deconfinement transition line extends into the (µ, T )-plane. It terminates at a critical endpoint which also is in the universality class of the 3-dimensional Ising model. At a first order phase transition the confined and deconfined phases coexist and are separated by confined-deconfined interfaces. -

A Quark-Meson Coupling Model for Nuclear and Neutron Matter
Adelaide University ADPT February A quarkmeson coupling mo del for nuclear and neutron matter K Saito Physics Division Tohoku College of Pharmacy Sendai Japan and y A W Thomas Department of Physics and Mathematical Physics University of Adelaide South Australia Australia March Abstract nucl-th/9403015 18 Mar 1994 An explicit quark mo del based on a mean eld description of nonoverlapping nucleon bags b ound by the selfconsistent exchange of ! and mesons is used to investigate the prop erties of b oth nuclear and neutron matter We establish a clear understanding of the relationship b etween this mo del which incorp orates the internal structure of the nucleon and QHD Finally we use the mo del to study the density dep endence of the quark condensate inmedium Corresp ondence to Dr K Saito email ksaitonuclphystohokuacjp y email athomasphysicsadelaideeduau Recently there has b een considerable interest in relativistic calculations of innite nuclear matter as well as dense neutron matter A relativistic treatment is of course essential if one aims to deal with the prop erties of dense matter including the equation of state EOS The simplest relativistic mo del for hadronic matter is the Walecka mo del often called Quantum Hadro dynamics ie QHDI which consists of structureless nucleons interacting through the exchange of the meson and the time comp onent of the meson in the meaneld approximation MFA Later Serot and Walecka extended the mo del to incorp orate the isovector mesons and QHDI I and used it to discuss systems like -

The Confinement Problem in Lattice Gauge Theory
The Confinement Problem in Lattice Gauge Theory J. Greensite 1,2 1Physics and Astronomy Department San Francisco State University San Francisco, CA 94132 USA 2Theory Group, Lawrence Berkeley National Laboratory Berkeley, CA 94720 USA February 1, 2008 Abstract I review investigations of the quark confinement mechanism that have been carried out in the framework of SU(N) lattice gauge theory. The special role of ZN center symmetry is emphasized. 1 Introduction When the quark model of hadrons was first introduced by Gell-Mann and Zweig in 1964, an obvious question was “where are the quarks?”. At the time, one could respond that the arXiv:hep-lat/0301023v2 5 Mar 2003 quark model was simply a useful scheme for classifying hadrons, and the notion of quarks as actual particles need not be taken seriously. But the absence of isolated quark states became a much more urgent issue with the successes of the quark-parton model, and the introduction, in 1972, of quantum chromodynamics as a fundamental theory of hadronic physics [1]. It was then necessary to suppose that, somehow or other, the dynamics of the gluon sector of QCD contrives to eliminate free quark states from the spectrum. Today almost no one seriously doubts that quantum chromodynamics confines quarks. Following many theoretical suggestions in the late 1970’s about how quark confinement might come about, it was finally the computer simulations of QCD, initiated by Creutz [2] in 1980, that persuaded most skeptics. Quark confinement is now an old and familiar idea, routinely incorporated into the standard model and all its proposed extensions, and the focus of particle phenomenology shifted long ago to other issues. -

Effective Field Theories of Heavy-Quark Mesons
Effective Field Theories of Heavy-Quark Mesons A thesis submitted to The University of Manchester for the degree of Doctor of Philosophy (PhD) in the faculty of Engineering and Physical Sciences Mohammad Hasan M Alhakami School of Physics and Astronomy 2014 Contents Abstract 10 Declaration 12 Copyright 13 Acknowledgements 14 1 Introduction 16 1.1 Ordinary Mesons......................... 21 1.1.1 Light Mesons....................... 22 1.1.2 Heavy-light Mesons.................... 24 1.1.3 Heavy-Quark Mesons................... 28 1.2 Exotic cc¯ Mesons......................... 31 1.2.1 Experimental and theoretical studies of the X(3872). 34 2 From QCD to Effective Theories 41 2.1 Chiral Symmetry......................... 43 2.1.1 Chiral Symmetry Breaking................ 46 2.1.2 Effective Field Theory.................. 57 2.2 Heavy Quark Spin Symmetry.................. 65 2.2.1 Motivation......................... 65 2.2.2 Heavy Quark Effective Theory.............. 69 3 Heavy Hadron Chiral Perturbation Theory 72 3.1 Self-Energies of Charm Mesons................. 78 3.2 Mass formula for non-strange charm mesons.......... 89 3.2.1 Extracting the coupling constant of even and odd charm meson transitions..................... 92 2 4 HHChPT for Charm and Bottom Mesons 98 4.1 LECs from Charm Meson Spectrum............... 99 4.2 Masses of the charm mesons within HHChPT......... 101 4.3 Linear combinations of the low energy constants........ 106 4.4 Results and Discussion...................... 108 4.5 Prediction for the Spectrum of Odd- and Even-Parity Bottom Mesons............................... 115 5 Short-range interactions between heavy mesons in frame- work of EFT 126 5.1 Uncoupled Channel........................ 127 5.2 Two-body scattering with a narrow resonance........ -

Quark Diagram Analysis of Bottom Meson Decays Emitting Pseudoscalar and Vector Mesons
Quark Diagram Analysis of Bottom Meson Decays Emitting Pseudoscalar and Vector Mesons Maninder Kaur†, Supreet Pal Singh and R. C. Verma Department of Physics, Punjabi University, Patiala – 147002, India. e-mail: [email protected], [email protected] and [email protected] Abstract This paper presents the two body weak nonleptonic decays of B mesons emitting pseudoscalar (P) and vector (V) mesons within the framework of the diagrammatic approach at flavor SU(3) symmetry level. Using the decay amplitudes, we are able to relate the branching fractions of B PV decays induced by both b c and b u transitions, which are found to be well consistent with the measured data. We also make predictions for some decays, which can be tested in future experiments. PACS No.:13.25.Hw, 11.30.Hv, 14.40.Nd †Corresponding author: [email protected] 1. Introduction At present, several groups at Fermi lab, Cornell, CERN, DESY, KEK and Beijing Electron Collider etc. are working to ensure wide knowledge of the heavy flavor physics. In future, a large quantity of new and accurate data on decays of the heavy flavor hadrons is expected which calls for their theoretical analysis. Being heavy, bottom hadrons have several channels for their decays, categorized as leptonic, semi-leptonic and hadronic decays [1-2]. The b quark is especially interesting in this respect as it has W-mediated transitions to both first generation (u) and second generation (c) quarks. Standard model provides satisfactory explanation of the leptonic and semileptonic decays but weak hadronic decays confronts serious problem as these decays experience strong interactions interferences [3-6]. -

Quarks and Their Discovery
Quarks and Their Discovery Parashu Ram Poudel Department of Physics, PN Campus, Pokhara Email: [email protected] Introduction charge (e) of one proton. The different fl avors of Quarks are the smallest building blocks of matter. quarks have different charges. The up (u), charm They are the fundamental constituents of all the (c) and top (t) quarks have electric charge +2e/3 hadrons. They have fractional electronic charge. and the down (d), strange (s) and bottom (b) quarks Quarks never exist alone in nature. They are always have charge -e/3; -e is the charge of an electron. The found in combination with other quarks or antiquark masses of these quarks vary greatly, and of the six, in larger particle of matter. By studying these larger only the up and down quarks, which are by far the particles, scientists have determined the properties lightest, appear to play a direct role in normal matter. of quarks. Protons and neutrons, the particles that make up the nuclei of the atoms consist of quarks. There are four forces that act between the quarks. Without quarks there would be no atoms, and without They are strong force, electromagnetic force, atoms, matter would not exist as we know it. Quarks weak force and gravitational force. The quantum only form triplets called baryons such as proton and of strong force is gluon. Gluons bind quarks or neutron or doublets called mesons such as Kaons and quark and antiquark together to form hadrons. The pi mesons. Quarks exist in six varieties: up (u), down electromagnetic force has photon as quantum that (d), charm (c), strange (s), bottom (b), and top (t) couples the quarks charge. -

Phenomenological Review on Quark–Gluon Plasma: Concepts Vs
Review Phenomenological Review on Quark–Gluon Plasma: Concepts vs. Observations Roman Pasechnik 1,* and Michal Šumbera 2 1 Department of Astronomy and Theoretical Physics, Lund University, SE-223 62 Lund, Sweden 2 Nuclear Physics Institute ASCR 250 68 Rez/Prague,ˇ Czech Republic; [email protected] * Correspondence: [email protected] Abstract: In this review, we present an up-to-date phenomenological summary of research developments in the physics of the Quark–Gluon Plasma (QGP). A short historical perspective and theoretical motivation for this rapidly developing field of contemporary particle physics is provided. In addition, we introduce and discuss the role of the quantum chromodynamics (QCD) ground state, non-perturbative and lattice QCD results on the QGP properties, as well as the transport models used to make a connection between theory and experiment. The experimental part presents the selected results on bulk observables, hard and penetrating probes obtained in the ultra-relativistic heavy-ion experiments carried out at the Brookhaven National Laboratory Relativistic Heavy Ion Collider (BNL RHIC) and CERN Super Proton Synchrotron (SPS) and Large Hadron Collider (LHC) accelerators. We also give a brief overview of new developments related to the ongoing searches of the QCD critical point and to the collectivity in small (p + p and p + A) systems. Keywords: extreme states of matter; heavy ion collisions; QCD critical point; quark–gluon plasma; saturation phenomena; QCD vacuum PACS: 25.75.-q, 12.38.Mh, 25.75.Nq, 21.65.Qr 1. Introduction Quark–gluon plasma (QGP) is a new state of nuclear matter existing at extremely high temperatures and densities when composite states called hadrons (protons, neutrons, pions, etc.) lose their identity and dissolve into a soup of their constituents—quarks and gluons. -
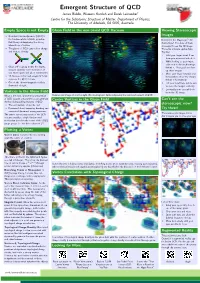
Emergent Structure Of
Emergent Structure of QCD James Biddle, Waseem Kamleh and Derek Leinwebery Centre for the Subatomic Structure of Matter, Department of Physics, The University of Adelaide, SA 5005, Australia Empty Space is not Empty Gluon Field in the non-trivial QCD Vacuum Viewing Stereoscopic Images Quantum Chromodynamics (QCD) is the fundamental relativistic quantum Remember the Magic Eye R 3D field theory underpinning the strong illustrations? You stare at them interactions of nature. cross-eyed to see the 3D image. The gluons of QCD carry colour charge The same principle applies here. and interact directly Try this! 1. Hold your finger about 5 cm from your nose and look at it. 2. While looking at your finger, take note of the double image Gluon self-coupling makes the empty behind it. Your goal is to line vacuum unstable to the formation of up those images. non-trivial quark and gluon condensates. 3. Move your finger forwards and 16 chromo-electric and -magnetic fields backwards to move the images compose the QCD vacuum. behind it horizontally. One of the chromo-magnetic fields is 4. Tilt your head from side to side illustrated at right. to move the images vertically. 5. Eventually your eyes will lock Vortices in the Gluon Field in on the 3D image. What is the most fundamental perspective Stereoscopic image of one the eight chromo-magnetic fields composing the nontrivial vacuum of QCD. of QCD vacuum structure that can generate Centre Vortices in the Gluon Field Can't see the the key distinguishing features of QCD stereoscopic view? The confinement of quarks, and Dynamical chiral symmetry breaking and Try these! associated dynamical-mass generation.