DOCSLIB.ORG

DIMENSIONS and UNITS to Get the Value of a Quantity in Gaussian Units, Multiply the Value Ex- Pressed in SI Units by the Conversion Factor

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
DIMENSIONS and UNITS to Get the Value of a Quantity in Gaussian Units, Multiply the Value Ex- Pressed in SI Units by the Conversion Factor DIMENSIONS AND UNITS To get the value of a quantity in Gaussian units, multiply the value ex- pressed in SI units by the conversion factor. Multiples of 3 intheconversion factors result from approximating the speed of light c =2.9979 1010 cm/sec × 3 1010 cm/sec. ≈ × Dimensions Physical Sym- SI Conversion Gaussian Quantity bol SI Gaussian Units Factor Units t2q2 Capacitance C l farad 9 1011 cm ml2 × m1/2l3/2 Charge q q coulomb 3 109 statcoulomb t × q m1/2 Charge ρ coulomb 3 103 statcoulomb 3 3/2 density l l t /m3 × /cm3 tq2 l Conductance siemens 9 1011 cm/sec ml2 t × 2 tq 1 9 1 Conductivity σ siemens 9 10 sec− 3 ml t /m × q m1/2l3/2 Current I,i ampere 3 109 statampere t t2 × q m1/2 Current J, j ampere 3 105 statampere 2 1/2 2 density l t l t /m2 × /cm2 m m 3 3 3 Density ρ kg/m 10− g/cm l3 l3 q m1/2 Displacement D coulomb 12π 105 statcoulomb l2 l1/2t /m2 × /cm2 1/2 ml m 1 4 Electric field E volt/m 10− statvolt/cm t2q l1/2t 3 × 2 1/2 1/2 ml m l 1 2 Electro- , volt 10− statvolt 2 motance EmfE t q t 3 × ml2 ml2 Energy U, W joule 107 erg t2 t2 m m Energy w, ϵ joule/m3 10 erg/cm3 2 2 density lt lt 10 Dimensions Physical Sym- SI Conversion Gaussian Quantity bol SI Gaussian Units Factor Units ml ml Force F newton 105 dyne t2 t2 1 1 Frequency f, ν hertz 1 hertz t t 2 ml t 1 11 Impedance Z ohm 10− sec/cm tq2 l 9 × 2 2 ml t 1 11 2 Inductance L henry 10− sec /cm q2 l 9 × Length l l l meter (m) 102 centimeter (cm) 1/2 q m 3 Magnetic H ampere– 4π 10− oersted 1/2 intensity lt l t turn/m × ml2 m1/2l3/2 Magnetic flux Φ weber 108 maxwell tq t m m1/2 Magnetic B tesla 104 gauss tq l1/2t induction l2q m1/2l5/2 Magnetic m, µ ampere–m2 103 oersted– t t moment cm3 1/2 q m 3 Magnetization M ampere– 4π 10− oersted lt l1/2t turn/m × q m1/2l1/2 4π Magneto- , ampere– gilbert 2 motance MmfM t t turn 10 Mass m, M m m kilogram 103 gram (g) (kg) ml ml Momentum p, P kg–m/s 105 g–cm/sec t t m m 2 1 2 Momentum kg/m –s 10− g/cm –sec l2t l2t density ml 1 Permeability µ 1 henry/m 107 — q2 4π × 11 Dimensions Physical Sym- SI Conversion Gaussian Quantity bol SI Gaussian Units Factor Units t2q2 Permittivity ϵ 1 farad/m 36π 109 — ml3 × q m1/2 Polarization P coulomb/m2 3 105 statcoulomb l2 l1/2t × /cm2 2 1/2 1/2 ml m l 1 2 Potential V,φ volt 10− statvolt t2q t 3 × ml2 ml2 Power P watt 107 erg/sec t3 t3 m m Power watt/m3 10 erg/cm3–sec lt3 lt3 density m m Pressure p, P pascal 10 dyne/cm2 lt2 lt2 2 q 1 9 1 Reluctance ampere–turn 4π 10− cm− 2 R ml l /weber × 2 ml t 1 11 Resistance R ohm 10− sec/cm tq2 l 9 × 3 ml 1 9 Resistivity η,ρ t ohm–m 10− sec tq2 9 × ml ml Thermal con- κ, k watt/m– 105 erg/cm–sec– 3 3 ductivity t t deg (K) deg (K) Time t t t second (s) 1 second (sec) ml m1/2l1/2 Vector A weber/m 106 gauss–cm potential tq t l l Velocity v m/s 102 cm/sec t t m m Viscosity η, µ kg/m–s 10 poise lt lt 1 1 1 1 Vorticity ζ s− 1 sec− t t ml2 ml2 Work W joule 107 erg t2 t2 12.
Load more

Recommended publications
  • Guide for the Use of the International System of Units (SI)
    Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S.
    [Show full text]
  • James Clerk Maxwell
    Conteúdo Páginas Henry Cavendish 1 Jacques Charles 2 James Clerk Maxwell 3 James Prescott Joule 5 James Watt 7 Jean-Léonard-Marie Poiseuille 8 Johann Heinrich Lambert 10 Johann Jakob Balmer 12 Johannes Robert Rydberg 13 John Strutt 14 Michael Faraday 16 Referências Fontes e Editores da Página 18 Fontes, Licenças e Editores da Imagem 19 Licenças das páginas Licença 20 Henry Cavendish 1 Henry Cavendish Referência : Ribeiro, D. (2014), WikiCiências, 5(09):0811 Autor: Daniel Ribeiro Editor: Eduardo Lage Henry Cavendish (1731 – 1810) foi um físico e químico que investigou isoladamente de acordo com a tradição de Sir Isaac Newton. Cavendish entrou no seminário em 1742 e frequentou a Universidade de Cambridge (1749 – 1753) sem se graduar em nenhum curso. Mesmo antes de ter herdado uma fortuna, a maior parte das suas despesas eram gastas em montagem experimental e livros. Em 1760, foi eleito Fellow da Royal Society e, em 1803, um dos dezoito associados estrangeiros do Institut de France. Entre outras investigações e descobertas de Cavendish, a maior ocorreu em 1781, quando compreendeu que a água é uma substância composta por hidrogénio e oxigénio, uma reformulação da opinião de há milénios de que a água é um elemento químico básico. O químico inglês John Warltire (1725/6 – 1810) realizou uma Figura 1 Henry Cavendish (1731 – 1810). experiência em que explodiu uma mistura de ar e hidrogénio, descobrindo que a massa dos gases residuais era menor do que a da mistura original. Ele atribuiu a perda de massa ao calor emitido na reação. Cavendish concluiu que algum erro substancial estava envolvido visto que não acreditava que, dentro da teoria do calórico, o calor tivesse massa suficiente, à escala em análise.
    [Show full text]
  • S.I. and Cgs Units
    Some Notes on SI vs. cgs Units by Jason Harlow Last updated Feb. 8, 2011 by Jason Harlow. Introduction Within “The Metric System”, there are actually two separate self-consistent systems. One is the Systme International or SI system, which uses Metres, Kilograms and Seconds for length, mass and time. For this reason it is sometimes called the MKS system. The other system uses centimetres, grams and seconds for length, mass and time. It is most often called the cgs system, and sometimes it is called the Gaussian system or the electrostatic system. Each system has its own set of derived units for force, energy, electric current, etc. Surprisingly, there are important differences in the basic equations of electrodynamics depending on which system you are using! Important textbooks such as Classical Electrodynamics 3e by J.D. Jackson ©1998 by Wiley and Classical Electrodynamics 2e by Hans C. Ohanian ©2006 by Jones & Bartlett use the cgs system in all their presentation and derivations of basic electric and magnetic equations. I think many theorists prefer this system because the equations look “cleaner”. Introduction to Electrodynamics 3e by David J. Griffiths ©1999 by Benjamin Cummings uses the SI system. Here are some examples of units you may encounter, the relevant facts about them, and how they relate to the SI and cgs systems: Force The SI unit for force comes from Newton’s 2nd law, F = ma, and is the Newton or N. 1 N = 1 kg·m/s2. The cgs unit for force comes from the same equation and is called the dyne, or dyn.
    [Show full text]
  • SI and CGS Units in Electromagnetism
    SI and CGS Units in Electromagnetism Jim Napolitano January 7, 2010 These notes are meant to accompany the course Electromagnetic Theory for the Spring 2010 term at RPI. The course will use CGS units, as does our textbook Classical Electro- dynamics, 2nd Ed. by Hans Ohanian. Up to this point, however, most students have used the International System of Units (SI, also known as MKSA) for mechanics, electricity and magnetism. (I believe it is easy to argue that CGS is more appropriate for teaching elec- tromagnetism to physics students.) These notes are meant to smooth the transition, and to augment the discussion in Appendix 2 of your textbook. The base units1 for mechanics in SI are the meter, kilogram, and second (i.e. \MKS") whereas in CGS they are the centimeter, gram, and second. Conversion between these base units and all the derived units are quite simply given by an appropriate power of 10. For electromagnetism, SI adds a new base unit, the Ampere (\A"). This leads to a world of complications when converting between SI and CGS. Many of these complications are philosophical, but this note does not discuss such issues. For a good, if a bit flippant, on- line discussion see http://info.ee.surrey.ac.uk/Workshop/advice/coils/unit systems/; for a more scholarly article, see \On Electric and Magnetic Units and Dimensions", by R. T. Birge, The American Physics Teacher, 2(1934)41. Electromagnetism: A Preview Electricity and magnetism are not separate phenomena. They are different manifestations of the same phenomenon, called electromagnetism. One requires the application of special relativity to see how electricity and magnetism are united.
    [Show full text]
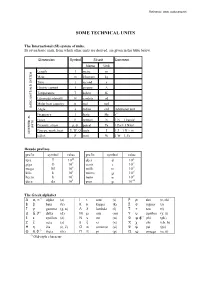
  • Technical Units
    Reference: www. rockmass.net 620(7(&+1,&$/81,76 7KH,QWHUQDWLRQDO 6, V\VWHPRIXQLWV Its seven basic units, from which other units are derived, are given in the table below. Dimension Symbol SI unit Comment Name Unit Length l metre m Mass m kilogram kg Time t second s Electric current I ampere A Temperature T kelvin K Luminous intensity Iv candela cd Molar heat capacity n mol mol BASIC UNITS IN SI SYSTEM Angle a radian rad Additional unit Frequency f hertz Hz s-1 Force F newton N 1 N = 1 kgm/s2 Pressure, stress p, σ, pascal Pa 1 Pa = 1 N/m² UNITS Energy, work, heat E, W, Q joule J 1 J = 1 N × m DIVERTED SI- Effect P watt W 1 W = 1 J/s 'HFDGHSUHIL[HV prefix symbol value prefix symbol value tera T 1012 deci d 10-1 giga G 109 centi c 10-2 mega M 106 milli m 10-3 kilo k 103 micro µ 10-6 hecto h 102 nano n 10-9 deca da 101 pico p 10-12 7KH*UHHNDOSKDEHW Α α, ∝ ∗) alpha (a) Ι ι iota (i) Ρ ρ rho (r, rh) Β β beta (b) Κ κ kappa (k) Σ σ sigma (s) Γ γ gamma (g, n) Λ λ lambda (l) Τ τ tau (t) ∆ δ, ∂ ∗) delta (d) Μ µ mu (m) Υ υ upsilon (y, u) Ε ε epsilon (e) Ν ν nu (n) Φ φ, ϕ*) phi (ph) Ζ ζ zeta (z) Ξ ξ xi (x) X χ chi (ch, h) Η η ëta (e, ë) Ο ο omicron (o) Ψ ψ psi (ps) Θ θ, ϑ ∗) theta (th) Π π pi (p) Ω ω omega (o, õ) *) Old-style character 2 9DULRXVXQLWVDQGFRQYHUVLRQV 'LPHQVLRQ 1DPH 6\PERO 8QLW &RQYHUVLRQ Time minute min s 1 h = 60 s hour h h 1 h = 60 min day day day 1 day = 24 h week wk wk 1 wk = 7 days year yr yr 1 yr = 365.242 days = 52.17 wk Length Angstrom A m 1 A = 10-10 m nautical mile n mile 1 n mile = 1852 m wave length λ m Force load G (P,W) N 1 kp = 9.807 N 2 o o 2 gravity g N 1 gn = 9.80665 m/s (exact, at 45 N; at 60 N g = 9.82 m/s ) atmosphere atm 1 atm Modulus elasticity modulus E Pa 1 kPa = 0.1 N/cm = 0.102 ton/m2 deformation modulus G Pa 1 MPa = 10,2 kg/cm2 shear modulus K Pa Density mass density ρ kg/m3 force density γ kN/m3 Flow Lugeon Lugeon l/min/m 1 Lugeon = approx.
    [Show full text]
  • The International System of Units (SI)
    NAT'L INST. OF STAND & TECH NIST National Institute of Standards and Technology Technology Administration, U.S. Department of Commerce NIST Special Publication 330 2001 Edition The International System of Units (SI) 4. Barry N. Taylor, Editor r A o o L57 330 2oOI rhe National Institute of Standards and Technology was established in 1988 by Congress to "assist industry in the development of technology . needed to improve product quality, to modernize manufacturing processes, to ensure product reliability . and to facilitate rapid commercialization ... of products based on new scientific discoveries." NIST, originally founded as the National Bureau of Standards in 1901, works to strengthen U.S. industry's competitiveness; advance science and engineering; and improve public health, safety, and the environment. One of the agency's basic functions is to develop, maintain, and retain custody of the national standards of measurement, and provide the means and methods for comparing standards used in science, engineering, manufacturing, commerce, industry, and education with the standards adopted or recognized by the Federal Government. As an agency of the U.S. Commerce Department's Technology Administration, NIST conducts basic and applied research in the physical sciences and engineering, and develops measurement techniques, test methods, standards, and related services. The Institute does generic and precompetitive work on new and advanced technologies. NIST's research facilities are located at Gaithersburg, MD 20899, and at Boulder, CO 80303.
    [Show full text]
  • 20 Coulomb's Law Of
    Coulomb’s Law of 20 Electrostatic Forces Charge Interactions Are Described by Coulomb’s Law Electrical interactions between charges govern much of physics, chemistry, and biology. They are the basis for chemical bonding, weak and strong. Salts dis- solve in water to form the solutions of charged ions that cover three-quarters of the Earth’s surface. Salt water forms the working fluid of living cells. pH and salts regulate the associations of proteins, DNA, cells, and colloids, and the conformations of biopolymers. Nervous systems would not function without ion fluxes. Electrostatic interactions are also important in batteries, corrosion, and electroplating. Charge interactions obey Coulomb’s law. When more than two charged par- ticles interact, the energies are sums of Coulombic interactions. To calculate such sums, we introduce the concepts of the electric field, Gauss’s law, and the electrostatic potential. With these tools, you can determine the electrostatic force exerted by one charged object on another, as when an ion interacts with a protein, DNA molecule, or membrane, or when a charged polymer changes conformation. Coulomb’s law was discovered in careful experiments by H Cavendish (1731–1810), J Priestley (1733–1804), and CA Coulomb (1736–1806) on macro- scopic objects such as magnets, glass rods, charged spheres, and silk cloths. Coulomb’s law applies to a wide range of size scales, including atoms, molecules, and biological cells. It states that the interaction energy u(r ) 385 between two charges in a vacuum is Cq q u(r ) = 1 2 , (20.1) r where q1 and q2 are the magnitudes of the two charges, r is the distance sep- arating them, and C = 1/4πε0 is a proportionality constant (see box below).
    [Show full text]
  • Manual of Style
    Manual Of Style 1 MANUAL OF STYLE TABLE OF CONTENTS CHAPTER 1 GENERAL PROVISIONS ...............3 101.0 Scope .............................................. 3 102.0 Codes and Standards..................... 3 103.0 Code Division.................................. 3 104.0 Table of Contents ........................... 4 CHAPTER 2 ADMINISTRATION .........................6 201.0 Administration ................................. 6 202.0 Chapter 2 Definitions ...................... 6 203.0 Referenced Standards Table ......... 6 204.0 Individual Chapter Administrative Text ......................... 6 205.0 Appendices ..................................... 7 206.0 Installation Standards ..................... 7 207.0 Extract Guidelines .......................... 7 208.0 Index ............................................... 9 CHAPTER 3 TECHNICAL STYLE .................... 10 301.0 Technical Style ............................. 10 302.0 Technical Rules ............................ 10 Table 302.3 Possible Unenforceable and Vague Terms ................................ 10 303.0 Health and Safety ........................ 11 304.0 Rules for Mandatory Documents .................................... 11 305.0 Writing Mandatory Requirements ............................... 12 Table 305.0 Typical Mandatory Terms............. 12 CHAPTER 4 EDITORIAL STYLE ..................... 14 401.0 Editorial Style ................................ 14 402.0 Definitions ...................................... 14 403.0 Units of Measure ............................ 15 404.0 Punctuation
    [Show full text]
  • Introduction to Electrostatics
    Introduction to Electrostatics Charles Augustin de Coulomb (1736 - 1806) December 23, 2000 Contents 1 Coulomb's Law 2 2 Electric Field 4 3 Gauss's Law 7 4 Di®erential Form of Gauss's Law 9 5 An Equation for E; the Scalar Potential 10 r £ 5.1 Conservative Potentials . 11 6 Poisson's and Laplace's Equations 13 7 Energy in the Electric Field; Capacitance; Forces 15 7.1 Conductors . 20 7.2 Forces on Charged Conductors . 22 1 8 Green's Theorem 27 8.1 Green's Theorem . 29 8.2 Applying Green's Theorem 1 . 30 8.3 Applying Green's Theorem 2 . 31 8.3.1 Greens Theorem with Dirichlet B.C. 34 8.3.2 Greens Theorem with Neumann B.C. 36 2 We shall follow the approach of Jackson, which is more or less his- torical. Thus we start with classical electrostatics, pass on to magneto- statics, add time dependence, and wind up with Maxwell's equations. These are then expressed within the framework of special relativity. The remainder of the course is devoted to a broad range of interesting and important applications. This development may be contrasted with the more formal and el- egant approach which starts from the Maxwell equations plus special relativity and then proceeds to work out electrostatics and magneto- statics - as well as everything else - as special cases. This is the method of e.g., Landau and Lifshitz, The Classical Theory of Fields. The ¯rst third of the course, i.e., Physics 707, deals with physics which should be familiar to everyone; what will perhaps not be familiar are the mathematical techniques and functions that will be introduced in order to solve certain kinds of problems.
    [Show full text]
  • Physics and Technology System of Units for Electrodynamics
    PHYSICS AND TECHNOLOGY SYSTEM OF UNITS FOR ELECTRODYNAMICS∗ M. G. Ivanov† Moscow Institute of Physics and Technology Dolgoprudny, Russia Abstract The contemporary practice is to favor the use of the SI units for electric circuits and the Gaussian CGS system for electromagnetic field. A modification of the Gaussian system of units (the Physics and Technology System) is suggested. In the Physics and Technology System the units of measurement for electrical circuits coincide with SI units, and the equations for the electromagnetic field are almost the same form as in the Gaussian system. The XXIV CGMP (2011) Resolution ¾On the possible future revision of the International System of Units, the SI¿ provides a chance to initiate gradual introduction of the Physics and Technology System as a new modification of the SI. Keywords: SI, International System of Units, electrodynamics, Physics and Technology System of units, special relativity. 1. Introduction. One and a half century dispute The problem of choice of units for electrodynamics dates back to the time of M. Faraday (1822–1831) and J. Maxwell (1861–1873). Electrodynamics acquired its final form only after geometrization of special relativity by H. Minkowski (1907–1909). The improvement of contemporary (4-dimentional relativistic covariant) formulation of electrodynamics and its implementation in practice of higher education stretched not less than a half of century. Overview of some systems of units, which are used in electrodynamics could be found, for example, in books [2, 3] and paper [4]. Legislation and standards of many countries recommend to use in science and education The International System of Units (SI).
    [Show full text]
  • Thermodynamics
    Thermodynamics D.G. Simpson, Ph.D. Department of Physical Sciences and Engineering Prince George’s Community College Largo, Maryland Spring 2013 Last updated: January 27, 2013 Contents Foreword 5 1WhatisPhysics? 6 2Units 8 2.1 SystemsofUnits....................................... 8 2.2 SIUnits........................................... 9 2.3 CGSSystemsofUnits.................................... 12 2.4 British Engineering Units . 12 2.5 UnitsasanError-CheckingTechnique............................ 12 2.6 UnitConversions...................................... 12 2.7 OddsandEnds........................................ 14 3 Problem-Solving Strategies 16 4 Temperature 18 4.1 Thermodynamics . 18 4.2 Temperature......................................... 18 4.3 TemperatureScales..................................... 18 4.4 AbsoluteZero........................................ 19 4.5 “AbsoluteHot”........................................ 19 4.6 TemperatureofSpace.................................... 20 4.7 Thermometry........................................ 20 5 Thermal Expansion 21 5.1 LinearExpansion...................................... 21 5.2 SurfaceExpansion...................................... 21 5.3 VolumeExpansion...................................... 21 6Heat 22 6.1 EnergyUnits......................................... 22 6.2 HeatCapacity........................................ 22 6.3 Calorimetry......................................... 22 6.4 MechanicalEquivalentofHeat............................... 22 7 Phases of Matter 23 7.1 Solid............................................
    [Show full text]
  • DIMENSIONS and UNITS to Get the Value of a Quantity in Gaussian Units, Multiply the Value Ex- Pressed in SI Units by the Conversion Factor
    DIMENSIONS AND UNITS To get the value of a quantity in Gaussian units, multiply the value ex- pressed in SI units by the conversion factor. Multiples of 3 in the conversion factors result from approximating the speed of light c = 2.9979 1010 cm/sec × 3 1010 cm/sec. ≈ × Dimensions Physical Sym- SI Conversion Gaussian Quantity bol SI Gaussian Units Factor Units t2q2 Capacitance C l farad 9 1011 cm ml2 × m1/2l3/2 Charge q q coulomb 3 109 statcoulomb t × q m1/2 Charge ρ coulomb 3 103 statcoulomb 3 3/2 density l l t /m3 × /cm3 tq2 l Conductance siemens 9 1011 cm/sec ml2 t × 2 tq 1 9 1 Conductivity σ siemens 9 10 sec− 3 ml t /m × q m1/2l3/2 Current I,i ampere 3 109 statampere t t2 × q m1/2 Current J, j ampere 3 105 statampere 2 1/2 2 density l t l t /m2 × /cm2 m m 3 3 3 Density ρ kg/m 10− g/cm l3 l3 q m1/2 Displacement D coulomb 12π 105 statcoulomb l2 l1/2t /m2 × /cm2 1/2 ml m 1 4 Electric field E volt/m 10− statvolt/cm t2q l1/2t 3 × 2 1/2 1/2 ml m l 1 2 Electro- , volt 10− statvolt 2 motance EmfE t q t 3 × ml2 ml2 Energy U, W joule 107 erg t2 t2 m m Energy w,ǫ joule/m3 10 erg/cm3 2 2 density lt lt 11 Dimensions Physical Sym- SI Conversion Gaussian Quantity bol SI Gaussian Units Factor Units ml ml Force F newton 105 dyne t2 t2 1 1 Frequency f,ν hertz 1 hertz t t 2 ml t 1 11 Impedance Z ohm 10− sec/cm tq2 l 9 × 2 2 ml t 1 11 2 Inductance L henry 10− sec /cm q2 l 9 × Length l l l meter (m) 102 centimeter (cm) 1/2 q m 3 Magnetic H ampere– 4π 10− oersted 1/2 intensity lt l t turn/m × ml2 m1/2l3/2 Magnetic flux Φ weber 108 maxwell tq t m m1/2 Magnetic
    [Show full text]