How Does Light Rail Transit Affect Urban Land Use?
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

2019 Annual Regional Park-And-Ride System
2019 ANNUAL REGIONAL PARK & RIDE SYSTEM REPORT JANUARY 2020 Prepared for: Metropolitan Council Metro Transit Minnesota Valley Transit Authority SouthWest Transit Maple Grove Transit Plymouth Metrolink Northstar Link Minnesota Department of Transportation Prepared by: Ari Del Rosario Metro Transit Engineering and Facilities, Planning and Urban Design Table of Contents Overview ......................................................................................................................................................3 Capacity Changes........................................................................................................................................6 System Capacity and Usage by Travel Corridor .........................................................................................7 Planned Capacity Expansion .......................................................................................................................8 About the System Survey ............................................................................................................................9 Appendix A: Facility Utilization Data .......................................................................................................10 Park & Ride System Data .....................................................................................................................10 Park & Pool System Data .....................................................................................................................14 Bike & Ride -

Maple Grove Transit 2016 “Expressbusservice”
Maple Grove Transit 2016 “Express Bus Service” Customer Survey Report of Results December 2016 Prepared by: 2955 Valmont Road • Suite 300 • Boulder, Colorado 80301 • t: 303-444-7863 • www.n-r-c.com Maple Grove Transit “Express Bus Service” Customer Survey December 2016 Table of Contents Executive Summary ................................................................................................................... 1 Survey Background ...................................................................................................................4 Survey Results ...........................................................................................................................4 Appendix A: Verbatim Responses to Open-ended Survey Questions .................................... 34 Appendix B: Select Results Compared by Respondent Race/Ethnicity .................................. 92 Appendix C: Copy of Survey Questionnaire .......................................................................... 107 National Research Center, Inc. Report of Results Prepared by Maple Grove Transit “Express Bus Service” Customer Survey December 2016 List of Tables Table 1: Question 1................................................................................................................................................ 4 Table 2: Question 2 ............................................................................................................................................... 4 Table 3: Question 3 Compared by Question 1 .................................................................................................... -

AGENDA I-494 Corridor Commission Board of Directors Meeting
AGENDA I-494 Corridor Commission Board of Directors Meeting Wednesday, September 9, 2020 – 7:30 a.m. Virtual Meeting via Zoom 7:30 Call to Order (Chair) 7:30 Review August 2020 Meeting Minutes 7:35 Treasurer’s Report (Sue Kotchevar) 7:45 Technical Report (Kate Meredith) 7:55 Legislative Update (Katy Sen) 8:15 MnDOT I-494 Area Updates (Amber Blanchard & Andrew Lutaya, MnDOT) 8:45 2021 Board Chair and Vice Chair Succession Planning (Chair, Madison) 9:00 Adjourn Next Meeting Date/Time: Wednesday, October 14th from 7:30 – 9:00 a.m. Format: Zoom I-494 Corridor Commission Board of Directors Meeting August 12, 2020 Draft Minutes Board Members Attending: Brad Aho, Mary Brindle, Jack Broz, David Lindahl, Simon Trautmann, Julie Wischnack Others Attending: Amber Blanchard, April Crockett, Hennepin County Commissioner Debbie Goettel, Sue Kotchevar, Andrew Lutaya, Michelle Leonard, Melissa Madison, Kate Meredith, Katy Sen Motion Passed: Approve July 10, 2020 regular meeting and July 29, 2020 special meeting minutes. Roll call vote: Councilmember Aho – aye Councilmember Baloga – absent Councilmember Brindle – aye Jack Broz – aye David Lindahl – aye Glen Markegard – absent Councilmember Schack – absent Andrew Scipioni – absent Councilmember Trautmann – aye Julie Wischnack – aye Treasurer Report Prepared by the City of Eden Prairie, presented by Sue Kotchevar. Review of July payment of claims. Motion Passed: Approve July 2020 check register and treasurer’s report as presented. Roll call vote taken on the July Check Register: Councilmember Aho – aye Councilmember Baloga – absent Councilmember Brindle – aye Jack Broz – aye David Lindahl – aye Glen Markegard – absent Councilmember Schack – absent Andrew Scipioni – absent Councilmember Trautmann – aye Julie Wischnack – aye The July check register was reviewed and approved. -

Public Engagement Summary Report #5
Public Engagement Summary Report #5 Detailed Analysis Results August 19 – October 12, 2017 Draft Locally Preferred Alternative October 13 – November 17, 2017 December 2017 This page is intentionally left blank. Riverview Corridor Pre-Project Development Study Table of Contents 1.0 INTRODUCTION ................................................................................................... 1 Detailed Analysis Results – August 19, 2017 through October 12, 2017 .......................................... 2 Draft LPA – October 13, 2017 through November 17, 2017 ............................................................. 2 2.0 PROJECT COMMITTEES ..................................................................................... 4 Policy Advisory Committee ................................................................................................................ 4 Technical Advisory Committee .......................................................................................................... 5 Project Management Team ............................................................................................................... 5 Public Engagement Advisory Panel ................................................................................................... 5 3.0 COMMUNITY MEETINGS ..................................................................................... 6 Open House + Public Hearing: November 9, 2017 ............................................................................ 6 3.1.1 Format .......................................................................................................................................... -

Transit Operations Plans Report
Transit Operations Plans Report Prepared for: Hennepin County Regional Railroad Authority Prepared by: Connetics Transportation Group Under Contract To: Kimley-Horn and Associates TABLE OF CONTENTS 1.0 INTRODUCTION ................................................................................................................................... 1 2.0 Existing Service Characteristics ......................................................................................................... 2 2.1 Bottineau Project Area Facilities ........................................................................................................ 2 2.2 Urban Local Routes ............................................................................................................................ 2 2.3 Suburban Local Routes ...................................................................................................................... 5 2.4 Limited Stop and Express Routes ...................................................................................................... 8 2.5 Routes operated by Maple Grove Transit ....................................................................................... 12 3.0 NO-BUILD ALTERNATIVE .................................................................................................................. 18 3.1 No-Build Operating Requirements .................................................................................................. 19 4.0 BASELINE ALTERNATIVE ................................................................................................................. -

Transit System
General Information Passes and Cards Transit Fares Transit System Map Holiday Service Contact Us Go-To Card Cash Fares Non-Rush Rush The Minnesota Valley Transit Authority Hours Hours MVTA routes do not operate on Thanks- Phone Numbers Go-To cards offer a fast and convenient way to pay tran- giving and Christmas. Weekend service sit fares. The durable, plastic card tracks cash value and (MVTA) is the public transportation 952-882-7500 MVTA Customer Service Adults operates on New Year’s Day, Memorial 31-day passes. Simply touch the Go-To card to the card Local Fare $1.75 $2.25 provider for the businesses and Day, Independence Day, and Labor Day. MVTA Customer Service representatives can reader and the appropriate fare is deducted automatically. Express Fare $2.25 $3.00 Special schedules operate on Good Friday, Christmas answer your questions about routes, schedules and fares; residents of Apple Valley, Burnsville, Go-To cards are rechargeable and are accepted on any Eve and the Friday after Thanksgiving – refer to web mail you schedules; and provide information about regular route bus, Blue Line and Green Line. Seniors (65+), and Youth (6-12) site or newsletters for details. Reduced service may ridesharing and regional transit services. Local Fare $ .75 $2.25 Eagan, Prior Lake, Rosemount, Savage SuperSavers operate on days before or after holidays – refer to 952-882-6000 Flex Route reservation line Express Fare $ .75 $3.00 www.mvta.com for details. SuperSaver 31-Day Passes offer unlimited bus riding for a and Shakopee. 952-882-7500 MVTA Lost & Found Effective February 2017 31 consecutive day period starting on the first day of use. -
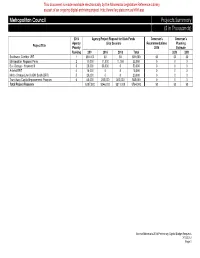
Metropolitan Council Projects Summary ($ in Thousands)
This document is made available electronically by the Minnesota Legislative Reference Library as part of an ongoing digital archiving project. http://www.leg.state.mn.us/lrl/lrl.asp Metropolitan Council Projects Summary ($ in Thousands) 2014 Agency Project Request for State Funds Governor’s Governor’s Agency ($ by Session) Recommendations Planning Project Title Priority 2014 Estimate Ranking 2014 2016 2018 Total 2016 2018 Southwest Corridor LRT 1 $81,000 $0 $0 $81,000 $0 $0 $0 Metropolitan Regional Parks 2 11,000 11,000 11,000 33,000 0 0 0 Bus Garage - Heywood II 3 20,000 30,000 0 50,000 0 0 0 Arterial BRT 4 15,000 0 0 15,000 0 0 0 Metro Orange Line (I-35W South BRT) 5 20,000 0 0 20,000 0 0 0 Transitway Capital Improvement Program 6 60,000 205,000 300,000 565,000 0 0 0 Total Project Requests $207,000 $246,000 $311,000 $764,000 $0 $0 $0 State of Minnesota 2014 Preliminary Capital Budget Requests 7/15/2013 Page 1 Metropolitan Council Project Narrative Southwest Corridor LRT 2014 STATE APPROPRIATION REQUEST: $81,000,000 downtown Minneapolis, and thereby providing a one-seat ride to the University of Minnesota, State Capitol area and downtown St. Paul. A total AGENCY PROJECT PRIORITY: 1 of 6 of 26 additional light rail vehicles would be required to operate the SWLRT line. The SWLRT line would require the construction of an Operations and Maintenance Facility. Project At A Glance With its interlining linkage to Central and Hiawatha LRT, Southwest LRT will The Southwest Light Rail Transit (LRT) Project is a proposed approximately provide direct, high quality LRT access to five of the region’s eight largest 15 mile extension of the Central Corridor LRT line from downtown business concentrations --- job centers each with over 40,000 employees. -

CEDAR AVENUE TRANSITWAY Implementation Plan Update
CEDAR AVENUE TRANSITWAY Implementation Plan Update EXECUTIVE SUMMARY DECEMBER 2015 Executive Summary In 2013, the Twin Cities metropolitan area’s first bus rapid What is Bus Rapid Transit? transit (BRT) line, the METRO Red Line, began station-to- station bus service between the Mall of America Station and Bus rapid transit (BRT) provides the Apple Valley Transit Station on the Cedar Avenue fast, frequent, all-day transit Transitway. The service operates every 15 minutes service. BRT stations include premium customer amenities throughout weekdays and every 30 minutes on weekends. similar to light rail transit (LRT) The implementation of the METRO Red Line was the stations, including radiant on- outcome of years of planning led by the Dakota County demand heat, ticket vending Regional Railroad Authority (DCRRA) and partners to machines, and real-time NexTrip identify the best transit customer information signage. alternative to serve the needs of the growing south metro communities of Burnsville, Eagan, Apple Valley, and Lakeville in Dakota County. The purpose of this 2015 Implementation Plan Update (IPU) is to identify service and facility improvements that address the many changing conditions in the corridor, community, and in the region. These changes include recent updates to forecasted employment growth, population growth, and land uses, which provide an opportunity to reassess the demand for transit service around the Cedar Avenue Transitway. Regionally, Counties Transit Improvement Board (CTIB) project funding eligibility and Metropolitan Council Regional Solicitation project prioritization and selection have also changed, which modifies the availability of these funds for the Cedar Avenue Transitway. As part of the current IPU, goals for the Cedar Avenue Transitway were revised based on feedback from policymakers to better reflect changing conditions in the corridor and in the region, including recent updates to forecasted employment growth, population growth, and land uses. -

January–June 2004 • $10.00 / Don Scott's Museum Chronicles • Light Rail in the Twin Cities
January–June 2004 • $10.00 / Don Scott’s Museum Chronicles • Light Rail in the Twin Cities 40 headlights | january–june 2004 LIGHT RAIL IN THE TWIN CITIES By Raymond R. t seemed an inglorious end of an era for the citizens of the Twin Berger (ERA #2298) Cities area, back on June 7, 1954. But that was about to change. At left, car 111 waits for time at the temporary southern Exactly 50 years, 19 days since the last streetcar rolled in Minneapolis, terminus, Forth Snelling, passengers were lining up to ride on the city’s new light rail line. on opening day of the Hiawatha Line. It will be ISo many, in fact, that some had to be turned away. The opening of the third in-service train the Hiawatha Line promissed to become one of the most significant northbound. Onlookers are taking pictures and waiting recent events in the history of electric railroading, the culmination for their turn to board. of studies, plans and setbacks spanning over three decades. Most are not old enough to remember when the Twin Cities was last served Opening Day by electric traction, some 50 years previously. Saturday, June 26, 2004 was a perfect day — sunny and mild — certainly befitting the glorious ray berger event that was finally taking place in Minneapolis. People gathered at the Warehouse District/ Hennepin Avenue station for the opening ceremony as soon as the sun had risen. This terminal station, gateway to the city’s entertainment district, was the site of speeches by public officials. It is also the starting point of a new light rail line connecting downtown Minneapolis with the Twin Cities’ most important traffic generators: the Minneapolis-Saint Paul International Airport (MSP) and the Mall of America, the largest shopping center in the United States. -

Community Exploration
Community Exploration MALL OF AMERICA Every year more than 40 million people go to the Mall of America. No other mall in the world can say the same! It is on the former site of Metropolitan Stadium where the Minnesota Vikings and Twins played until 1982. Attractions include more than 520 stores (with no sales tax on clothing), Nickelodeon Universe, SEA LIFE Aquarium, LEGO Imagination Center, Adventure Mini Golf, more than 50 restaurants, and a movie theater. How to get there: Board the METRO Green Line from any of the three campus light rail stations traveling west to the Downtown East Station where the new Minnesota Vikings stadium is currently under construction. At the Downtown East Station, get off the METRO Green Line train and get on the METRO Blue Line going south and ride to the Mall of America Station. U of M Free Ride Weekend: This weekend Metro Transit is hosting a U of M Free Ride Weekend. University of Minnesota students can ride free on all Metro Transit buses and METRO lines (not valid on Northstar Commuter Rail) from 6:00 p.m. Friday, August 29 to 11:59 p.m. Sunday, August 31. Students must show their U Cards in order to ride free or they may be subject to fines. Show your U Card to the bus driver when you board a bus and to Transit Police officers on METRO lines if asked. If you need assistance: If you get lost or need assistance, call the Metro Transit help line: 612-373-3333. Safety and etiquette: Light rail trains weigh around 100 tons each and are very quiet, so it is very important to obey warning signs and comply with all barriers and street signals. -

Gmetrotransit
,G MetroTransit a service ofthe Metropolitan Council 04 - 0544 Hiawatha Light Rail Transit Systern Transportation & Maintenance Operations Plan June 2004 ©Metropolitan Council 2004 HIAWATHA CORRIDOR LIGHT RAIL TRANSIT PROJECT TRANSPORTATION AND MAINTENANCE OPERATIONS PLAN (TMOP) TABLE OF CONTENTS PAGE GLOSSARY i 1.00.00 HIAWATHA CORRiDOR LIGHT RAIL TRANSIT PROJECT 1-1 1.01.00 Purpose of Plan 1-1 1.02.00 Relationship to Overall Transportation Network 1-1 1.03.00 Organization of the Operations Plan 1-2 2.00.00 SYSTEM DESCRIPTION 2-1 2.01.00 Alignment 2-1 Figure 2-1 Alignment of the Hiawatha Line 2-2 2.01.01 Stations 2-3 2.01.02 Yard and Shop 2-3 2.01.03 Special Trackwork 2-3 2.02.00 Interface with Other Transportation Modes 2-4 2.02.01 Sector 5 Reorganization 2-4 Table 2-1 Proposed 2004 Bus Route Connections at Rail Stations 2-6 2.02.02 General Traffic 2-7 Table 2-2 Grade Crossing Locations 2-8 2.03.00 Hours of Operation 2-9 2.04.00 Vehicle Loading Standards 2-9 2.05.00 Travel Times 2-9 2.05.01 Vehicle Performance Characteristics 2-9 2.05.02 Travel Times 2-10 2.06.00 Ridership Projections 2-10 2.06.01 Opening Year (2004) Ridership 2-11 Table 2-3 Hiawatha LRT Estimated Boardings/Alightings for the Year 2004 P.M. 2-12 Peak Hour 2.06.02 Design Year 2020 Ridership 2-13 Table 2-4 Hiwatha LRT Estimated Boardings/Alightings for the Year 2020 P.M. -

442 Is a Local Route Between Burnsville, [email protected] SENIORS (65+) Local Fare $1.00 $2.50 the Map
HOLIDAY SERVICE For more information on routes, LOCAL MVTA often operates with a reduced services, payment options and more: Plan! ROUTE IMPORTANT: Holiday Service Ride! schedule on holidays and holiday If paying in cash, use exact change – VISIT MVTA often operates with a reduced 1 Find the timetable for the correct day of Use MVTA’s Online Trip Planner, located Be prepared: arrive at your stop fi ve weeks. For reduced schedule drivers cannot make change. week and direction of travel. mvta.com schedule on holidays and holiday on our homepage, mvta.com minutes early and have your payment information, visit mvta.com or call MONDAY – FRIDAY 952-882-7500. — weeks. For reduced schedule 2 Find the locations (TimePoints) nearest ready when boarding. WEEKEND NON- Call the MVTA customer service phone CALL information, visit mvta.com or call your starting point and destination. RUSH RUSH line at 952-882-7500. Identify yourself: Wave at the bus 952-882-7500 Local Fare $2.00 $2.50 952-882-7500. Sign up for route alerts Remember that you may get on and off at mvta.com. the bus at transit stops between the when it arrives to make it clear to the COVID-19 INFORMATION Effective 5/15/2021 — ADULTS Express Download the free Ride MVTA app $2.50 $3.25 TimePoints. The TimePoint letters ( A ) driver that you would like to board. MVTA has been promoting health experts’ EMAIL Fare at Google Play or the App Store for Bicycle Information provide a reference to the locations on Most of MVTA’s buses will stop at any recommendations and social distancing 442 is a local route between Burnsville, [email protected] SENIORS (65+) Local Fare $1.00 $2.50 the map.