Kepler Towers, Catalan Numbers and Strahler Distribution
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Craters in Shadow
Section 3: Craters in Shadow Kepler Copernicus Eratosthenes Seen it Clavius Seen it Section 3: Craters in Shadow Visibility: A pair of binoculars is the minimum requirement to see these features. When: Look for them when the terminator’s close by, typically a day before last quarter. Not all craters are best seen when the Sun is high in the lunar sky - in fact most aren’t! If craters aren’t par- ticularly bright or dark, they tend to disappear into the background when the Moon’s phase is close to full. These craters are best seen when the ‘terminator’ is nearby, or when the Sun is low in the lunar sky as seen from the crater. This causes oblique lighting to fall on the crater and create exaggerated shadows. Ultimately, this makes the crater look more dramatic and easier to see. We’ll use this effect for the next section on lunar mountains, but before we do, there are a couple of craters that we’d like to bring to your attention. Actually, the Moon is covered with a whole host of wonderful craters that look amazing when the lighting is oblique. During the summer and into the early autumn, it’s the later phases of the Moon are best positioned in the sky - the phases following full Moon. Unfortunately, this means viewing in the early hours but don’t worry as we’ve kept things simple. We just want to give you a taste of what a shadowed crater looks like for this marathon, so the going here is really pretty easy! First, locate the two craters Kepler and Copernicus which were marathon targets pointed out in Section 2. -
List of Missions Using SPICE (PDF)
1/7/20 Data Restorations Selected Past Users Current/Pending Users Examples of Possible Future Users Apollo 15, 16 [L] Magellan [L] Cassini Orbiter NASA Discovery Program Mariner 2 [L] Clementine (NRL) Mars Odyssey NASA New Frontiers Program Mariner 9 [L] Mars 96 (RSA) Mars Exploration Rover Lunar IceCube (Moorehead State) Mariner 10 [L] Mars Pathfinder Mars Reconnaissance Orbiter LunaH-Map (Arizona State) Viking Orbiters [L] NEAR Mars Science Laboratory Luna-Glob (RSA) Viking Landers [L] Deep Space 1 Juno Aditya-L1 (ISRO) Pioneer 10/11/12 [L] Galileo MAVEN Examples of Users not Requesting NAIF Help Haley armada [L] Genesis SMAP (Earth Science) GOLD (LASP, UCF) (Earth Science) [L] Phobos 2 [L] (RSA) Deep Impact OSIRIS REx Hera (ESA) Ulysses [L] Huygens Probe (ESA) [L] InSight ExoMars RSP (ESA, RSA) Voyagers [L] Stardust/NExT Mars 2020 Emmirates Mars Mission (UAE via LASP) Lunar Orbiter [L] Mars Global Surveyor Europa Clipper Hayabusa-2 (JAXA) Helios 1,2 [L] Phoenix NISAR (NASA and ISRO) Proba-3 (ESA) EPOXI Psyche Parker Solar Probe GRAIL Lucy EUMETSAT GEO satellites [L] DAWN Lunar Reconnaissance Orbiter MOM (ISRO) Messenger Mars Express (ESA) Chandrayan-2 (ISRO) Phobos Sample Return (RSA) ExoMars 2016 (ESA, RSA) Solar Orbiter (ESA) Venus Express (ESA) Akatsuki (JAXA) STEREO [L] Rosetta (ESA) Korean Pathfinder Lunar Orbiter (KARI) Spitzer Space Telescope [L] [L] = limited use Chandrayaan-1 (ISRO) New Horizons Kepler [L] [S] = special services Hayabusa (JAXA) JUICE (ESA) Hubble Space Telescope [S][L] Kaguya (JAXA) Bepicolombo (ESA, JAXA) James Webb Space Telescope [S][L] LADEE Altius (Belgian earth science satellite) ISO [S] (ESA) Armadillo (CubeSat, by UT at Austin) Last updated: 1/7/20 Smart-1 (ESA) Deep Space Network Spectrum-RG (RSA) NAIF has or had project-supplied funding to support mission operations, consultation for flight team members, and SPICE data archive preparation. -

10Great Features for Moon Watchers
Sinus Aestuum is a lava pond hemming the Imbrium debris. Mare Orientale is another of the Moon’s large impact basins, Beginning observing On its eastern edge, dark volcanic material erupted explosively and possibly the youngest. Lunar scientists think it formed 170 along a rille. Although this region at first appears featureless, million years after Mare Imbrium. And although “Mare Orien- observe it at several different lunar phases and you’ll see the tale” translates to “Eastern Sea,” in 1961, the International dark area grow more apparent as the Sun climbs higher. Astronomical Union changed the way astronomers denote great features for Occupying a region below and a bit left of the Moon’s dead lunar directions. The result is that Mare Orientale now sits on center, Mare Nubium lies far from many lunar showpiece sites. the Moon’s western limb. From Earth we never see most of it. Look for it as the dark region above magnificent Tycho Crater. When you observe the Cauchy Domes, you’ll be looking at Yet this small region, where lava plains meet highlands, con- shield volcanoes that erupted from lunar vents. The lava cooled Moon watchers tains a variety of interesting geologic features — impact craters, slowly, so it had a chance to spread and form gentle slopes. 10Our natural satellite offers plenty of targets you can spot through any size telescope. lava-flooded plains, tectonic faulting, and debris from distant In a geologic sense, our Moon is now quiet. The only events by Michael E. Bakich impacts — that are great for telescopic exploring. -
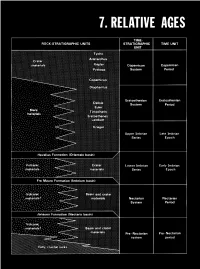
Relative Ages
CONTENTS Page Introduction ...................................................... 123 Stratigraphic nomenclature ........................................ 123 Superpositions ................................................... 125 Mare-crater relations .......................................... 125 Crater-crater relations .......................................... 127 Basin-crater relations .......................................... 127 Mapping conventions .......................................... 127 Crater dating .................................................... 129 General principles ............................................. 129 Size-frequency relations ........................................ 129 Morphology of large craters .................................... 129 Morphology of small craters, by Newell J. Fask .................. 131 D, method .................................................... 133 Summary ........................................................ 133 table 7.1). The first three of these sequences, which are older than INTRODUCTION the visible mare materials, are also dominated internally by the The goals of both terrestrial and lunar stratigraphy are to inte- deposits of basins. The fourth (youngest) sequence consists of mare grate geologic units into a stratigraphic column applicable over the and crater materials. This chapter explains the general methods of whole planet and to calibrate this column with absolute ages. The stratigraphic analysis that are employed in the next six chapters first step in reconstructing -

Astrophysics
National Aeronautics and Space Administration Astrophysics Committee on NASA Science Paul Hertz Mission Extensions Director, Astrophysics Division NRC Keck Center Science Mission Directorate Washington DC @PHertzNASA February 1-2, 2016 Why Astrophysics? Astrophysics is humankind’s scientific endeavor to understand the universe and our place in it. 1. How did our universe 2. How did galaxies, stars, 3. Are We Alone? begin and evolve? and planets come to be? These national strategic drivers are enduring 1972 1982 1991 2001 2010 2 Astrophysics Driving Documents http://science.nasa.gov/astrophysics/documents 3 Astrophysics Programs Physics of the Cosmos Cosmic Origins Exoplanet Exploration Program Program Program 1. How did our universe 2. How did galaxies, stars, 3. Are We Alone? begin and evolve? and planets come to be? Astrophysics Explorers Program Astrophysics Research Program James Webb Space Telescope Program (managed outside of Astrophysics Division until commissioning) 4 Astrophysics Programs and Missions Physics of the Cosmos Cosmic Origins Exoplanet Exploration Program Program Program Chandra Hubble Spitzer Kepler/K2 XMM-Newton (ESA) Herschel (ESA) WFIRST Fermi SOFIA Planck (ESA) LISA Pathfinder (ESA) Astrophysics Explorers Program Euclid (ESA) NuSTAR Swift Suzaku (JAXA) Athena (ESA) ASTRO-H (JAXA) NICER TESS L3 GW Obs (ESA) 3 SMEX and 2 MO in Phase A James Webb Space Telescope Program: Webb 5 Astrophysics Programs and Missions Physics of the Cosmos Cosmic Origins Exoplanet Exploration Program Program Program Missions in extended phase Chandra Hubble Spitzer Kepler/K2 XMM-Newton (ESA) Herschel (ESA) WFIRST Fermi SOFIA Planck (ESA) LISA Pathfinder (ESA) Astrophysics Explorers Program Euclid (ESA) NuSTAR Swift Suzaku (JAXA) Athena (ESA) ASTRO-H (JAXA) NICER TESS L3 GW Obs (ESA) 3 SMEX and 2 MO in Phase A James Webb Space Telescope Program: Webb 6 Astrophysics Mission Portfolio • NASA Astrophysics seeks to advance NASA’s strategic objectives in astrophysics as well as the science priorities of the Decadal Survey in Astronomy and Astrophysics. -

Issue #1 – 2012 October
TTSIQ #1 page 1 OCTOBER 2012 Introducing a new free quarterly newsletter for space-interested and space-enthused people around the globe This free publication is especially dedicated to students and teachers interested in space NEWS SECTION pp. 3-22 p. 3 Earth Orbit and Mission to Planet Earth - 13 reports p. 8 Cislunar Space and the Moon - 5 reports p. 11 Mars and the Asteroids - 5 reports p. 15 Other Planets and Moons - 2 reports p. 17 Starbound - 4 reports, 1 article ---------------------------------------------------------------------------------------------------- ARTICLES, ESSAYS & MORE pp. 23-45 - 10 articles & essays (full list on last page) ---------------------------------------------------------------------------------------------------- STUDENTS & TEACHERS pp. 46-56 - 9 articles & essays (full list on last page) L: Remote sensing of Aerosol Optical Depth over India R: Curiosity finds rocks shaped by running water on Mars! L: China hopes to put lander on the Moon in 2013 R: First Square Kilometer Array telescopes online in Australia! 1 TTSIQ #1 page 2 OCTOBER 2012 TTSIQ Sponsor Organizations 1. About The National Space Society - http://www.nss.org/ The National Space Society was formed in March, 1987 by the merger of the former L5 Society and National Space institute. NSS has an extensive chapter network in the United States and a number of international chapters in Europe, Asia, and Australia. NSS hosts the annual International Space Development Conference in May each year at varying locations. NSS publishes Ad Astra magazine quarterly. NSS actively tries to influence US Space Policy. About The Moon Society - http://www.moonsociety.org The Moon Society was formed in 2000 and seeks to inspire and involve people everywhere in exploration of the Moon with the establishment of civilian settlements, using local resources through private enterprise both to support themselves and to help alleviate Earth's stubborn energy and environmental problems. -

A Lunar Retreat
University of Calgary PRISM: University of Calgary's Digital Repository Graduate Studies Legacy Theses 2001 Transcending space: a lunar retreat Fortin, David T. Fortin, D. T. (2001). Transcending space: a lunar retreat (Unpublished master's thesis). University of Calgary, Calgary, AB. doi:10.11575/PRISM/17027 http://hdl.handle.net/1880/40867 master thesis University of Calgary graduate students retain copyright ownership and moral rights for their thesis. You may use this material in any way that is permitted by the Copyright Act or through licensing that has been assigned to the document. For uses that are not allowable under copyright legislation or licensing, you are required to seek permission. Downloaded from PRISM: https://prism.ucalgary.ca The author of this thesis has granted the University of Calgary a non-exclusive license to reproduce and distribute copies of this thesis to users of the University of Calgary Archives. Copyright remains with the author. Theses and dissertations available in the University of Calgary Institutional Repository are solely for the purpose of private study and research. They may not be copied or reproduced, except as permitted by copyright laws, without written authority of the copyright owner. Any commercial use or publication is strictly prohibited. The original Partial Copyright License attesting to these terms and signed by the author of this thesis may be found in the original print version of the thesis, held by the University of Calgary Archives. The thesis approval page signed by the examining committee may also be found in the original print version of the thesis held in the University of Calgary Archives. -

Kepler Press
National Aeronautics and Space Administration PRESS KIT/FEBRUARY 2009 Kepler: NASA’s First Mission Capable of Finding Earth-Size Planets www.nasa.gov Media Contacts J.D. Harrington Policy/Program Management 202-358-5241 NASA Headquarters [email protected] Washington 202-262-7048 (cell) Michael Mewhinney Science 650-604-3937 NASA Ames Research Center [email protected] Moffett Field, Calif. 650-207-1323 (cell) Whitney Clavin Spacecraft/Project Management 818-354-4673 Jet Propulsion Laboratory [email protected] Pasadena, Calif. 818-458-9008 (cell) George Diller Launch Operations 321-867-2468 Kennedy Space Center, Fla. [email protected] 321-431-4908 (cell) Roz Brown Spacecraft 303-533-6059. Ball Aerospace & Technologies Corp. [email protected] Boulder, Colo. 720-581-3135 (cell) Mike Rein Delta II Launch Vehicle 321-730-5646 United Launch Alliance [email protected] Cape Canaveral Air Force Station, Fla. 321-693-6250 (cell) Contents Media Services Information .......................................................................................................................... 5 Quick Facts ................................................................................................................................................... 7 NASA’s Search for Habitable Planets ............................................................................................................ 8 Scientific Goals and Objectives ................................................................................................................. -

Producing Transformative Lunar Science with Geologic Sample Return: a Note About Sample Mass
Lunar Surface Science Workshop 2020 (LPI Contrib. No. 2241) 5037.pdf PRODUCING TRANSFORMATIVE LUNAR SCIENCE WITH GEOLOGIC SAMPLE RETURN: A NOTE ABOUT SAMPLE MASS. David A. Kring1,2, 1Center for Lunar Science and Exploration, Lunar and Planetary Institute, Universities Space Research Association, 3600 Bay Area Blvd., Houston TX 77058 USA ([email protected]), 2NASA Solar System Exploration Research Virtual Institute. Introduction: The big ideas to emerge from Apollo Potential Mass of the Investigation: There are are a product of sample return: (1) The chemical three components to the mass required for a sample composition of lunar samples forced the community to return investigation. reconsider the origin of the Earth-Moon system, Geologic tools (to surface). Tool kits including spawning the giant impact hypothesis. (2) A few bright- hammers (est. 1.3 kg), tongs (est. 0.2 kg), scoops (est. white clasts in Apollo 11 soils, deftly interpreted to be 0.6 kg), rakes (est. 1.5 kg), and extension handles (est. impact-excavated debris from the distant highlands, led 0.8 kg) will be needed on the descent manifest, but will to the lunar magma ocean hypothesis. (3) A bevy of not be returned to Earth. Cameras will also be needed ~3.9 to 4.0 Ga impact ages in samples from several for sample documentation and interaction between crew Apollo sites prompted the lunar cataclysm hypothesis, and a supporting science operations staff. which is now more broadly understood to be a Solar Geologic samples (from surface). Estimating System-wide event, although the magnitude and sample return mass can be done using (1) historical data duration of bombardment continue to be debated. -

Astrophysics Division Update Presented to the Astronomy & Astrophysics Advisory Committee
Astrophysics Division Update Presented to the Astronomy & Astrophysics Advisory Committee Dr. Jon Morse Director, Astrophysics Division Science Mission Directorate NASA Headquarters 22 February 2011 Outline • Science Highlights • Programmatic Update • Budget Update • Issues and Concerns 2 Hubble Finds Most Distant Galaxy Candidate Ever Seen in Universe The farthest and one of the very earliest galaxies ever seen in the universe appears as a faint red blob in this ultra-deep–field exposure taken with NASA's Hubble Space Telescope. This is the deepest infrared image taken of the universe. Based on the object's color, astronomers believe it is 13.2 billion light-years away. The proto-galaxy is only visible at the farthest infrared wavelengths observable by Hubble. Observations of earlier times, when the first stars and galaxies were forming, will require Hubble‟s successor, the James Webb Space Telescope (JWST). 3 Kepler Mission Data Release New Data Released to Public Six New Exoplanets Confirmed Previous New • Kepler has released data on 155,453 stars and on the • Kepler has found six confirmed planets orbiting a sun-like 1,235 planetary candidates that it has discovered in the star, Kepler-11, located ~2000 light years from Earth. first 4 months of science operations. • This is the largest group of transiting planets orbiting a • The planetary candidates include: 68 of Earth-size, 288 single star yet discovered outside our solar system. of super-Earth-size, 662 of Neptune-size, 165 of Jupiter- • The five inner planets comprise the most closely-spaced size, and 19 larger than Jupiter. planetary system known, with orbits smaller than • 54 planetary candidates are in the habitable zone of Mercury‟s. -

Radial Velocity Transit Animation by European Southern Observatory Animation by NASA Goddard Media Studios
Courtney Dressing Assistant Professor at UC Berkeley The Space Astrophysics Landscape for the 2020s and Beyond April 1, 2019 Credit: NASA David Charbonneau (Co-Chair), Scott Gaudi (Co-Chair), Fabienne Bastien, Jacob Bean, Justin Crepp, Eliza Kempton, Chryssa Kouveliotou, Bruce Macintosh, Dimitri Mawet, Victoria Meadows, Ruth Murray-Clay, Evgenya Shkolnik, Ignas Snellen, Alycia Weinberger Exoplanet Discoveries Have Increased Dramatically Figure Credit: A. Weinberger (ESS Report) What Do We Know Today? (Statements from the ESS Report) • “Planetary systems are ubiquitous and surprisingly diverse, and many bear no resemblance to the Solar System.” • “A significant fraction of planets appear to have undergone large-scale migration from their birthsites.” • “Most stars have planets, and small planets are abundant.” • “Large numbers of rocky planets [have] been identified and a few habitable zone examples orbiting nearby small stars have been found.” • “Massive young Jovians at large separations have been imaged.” • “Molecules and clouds in the atmospheres of large exoplanets have been detected.” • ”The identification of potential false positives and negatives for atmospheric biosignatures has improved the biosignature observing strategy and interpretation framework.” Radial Velocity Transit Animation by European Southern Observatory Animation by NASA Goddard Media Studios How Did We Learn Those Lessons? Astrometry Direct Imaging Microlensing Animation by Exoplanet Exploration Office at NASA JPL Animation by Jason Wang Animation by Exoplanet Exploration Office at NASA JPL Exoplanet Science in the 2020s & Beyond The ESS Report Identified Two Goals 1. “Understand the formation and evolution of planetary systems as products of the process of star formation, and characterize and explain the diversity of planetary system architectures, planetary compositions, and planetary environments produced by these processes.” 2. -

China Dream, Space Dream: China's Progress in Space Technologies and Implications for the United States
China Dream, Space Dream 中国梦,航天梦China’s Progress in Space Technologies and Implications for the United States A report prepared for the U.S.-China Economic and Security Review Commission Kevin Pollpeter Eric Anderson Jordan Wilson Fan Yang Acknowledgements: The authors would like to thank Dr. Patrick Besha and Dr. Scott Pace for reviewing a previous draft of this report. They would also like to thank Lynne Bush and Bret Silvis for their master editing skills. Of course, any errors or omissions are the fault of authors. Disclaimer: This research report was prepared at the request of the Commission to support its deliberations. Posting of the report to the Commission's website is intended to promote greater public understanding of the issues addressed by the Commission in its ongoing assessment of U.S.-China economic relations and their implications for U.S. security, as mandated by Public Law 106-398 and Public Law 108-7. However, it does not necessarily imply an endorsement by the Commission or any individual Commissioner of the views or conclusions expressed in this commissioned research report. CONTENTS Acronyms ......................................................................................................................................... i Executive Summary ....................................................................................................................... iii Introduction ................................................................................................................................... 1