Phase Transitions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Sounds of a Supersolid A
NEWS & VIEWS RESEARCH hypothesis came from extensive population humans, implying possible mosquito exposure long-distance spread of insecticide-resistant time-series analysis from that earlier study5, to malaria parasites and the potential to spread mosquitoes, worsening an already dire situ- which showed beyond reasonable doubt that infection over great distances. ation, given the current spread of insecticide a mosquito vector species called Anopheles However, the authors failed to detect resistance in mosquito populations. This would coluzzii persists locally in the dry season in parasite infections in their aerially sampled be a matter of great concern because insecticides as-yet-undiscovered places. However, the malaria vectors, a result that they assert is to be are the best means of malaria control currently data were not consistent with this outcome for expected given the small sample size and the low available8. However, long-distance migration other malaria vectors in the study area — the parasite-infection rates typical of populations of could facilitate the desirable spread of mosqui- species Anopheles gambiae and Anopheles ara- malaria vectors. A problem with this argument toes for gene-based methods of malaria-vector biensis — leaving wind-powered long-distance is that the typical infection rates they mention control. One thing is certain, Huestis and col- migration as the only remaining possibility to are based on one specific mosquito body part leagues have permanently transformed our explain the data5. (salivary glands), rather than the unknown but understanding of African malaria vectors and Both modelling6 and genetic studies7 undoubtedly much higher infection rates that what it will take to conquer malaria. -

Current Status of Equation of State in Nuclear Matter and Neutron Stars
Open Issues in Understanding Core Collapse Supernovae June 22-24, 2004 Current Status of Equation of State in Nuclear Matter and Neutron Stars J.R.Stone1,2, J.C. Miller1,3 and W.G.Newton1 1 Oxford University, Oxford, UK 2Physics Division, ORNL, Oak Ridge, TN 3 SISSA, Trieste, Italy Outline 1. General properties of EOS in nuclear matter 2. Classification according to models of N-N interaction 3. Examples of EOS – sensitivity to the choice of N-N interaction 4. Consequences for supernova simulations 5. Constraints on EOS 6. High density nuclear matter (HDNM) 7. New developments Equation of State is derived from a known dependence of energy per particle of a system on particle number density: EA/(==En) or F/AF(n) I. E ( or Boltzman free energy F = E-TS for system at finite temperature) is constructed in a form of effective energy functional (Hamiltonian, Lagrangian, DFT/EFT functional or an empirical form) II. An equilibrium state of matter is found at each density n by minimization of E (n) or F (n) III. All other related quantities like e.g. pressure P, incompressibility K or entropy s are calculated as derivatives of E or F at equilibrium: 2 ∂E ()n ∂F ()n Pn()= n sn()=− | ∂n ∂T nY, p ∂∂P()nnEE() ∂2 ()n Kn()==9 18n +9n2 ∂∂nn∂n2 IV. Use as input for model simulations (Very) schematic sequence of equilibrium phases of nuclear matter as a function of density: <~2x10-4fm-3 ~2x10-4 fm-3 ~0.06 fm-3 Nuclei in Nuclei in Neutron electron gas + ‘Pasta phase’ Electron gas ~0.1 fm-3 0.3-0.5 fm-3 >0.5 fm-3 Nucleons + n,p,e,µ heavy baryons Quarks ??? -

Bose-Einstein Condensation
Physics monitor The oldest galaxy, as seen by the European Southern Observatory's NTT telescope. The left picture shows the target quasar, with right, the quasar image removed to make the galaxy, situated just to the north-west of the quasar, easier to see. superfluidity. Condensates could also play an important role in particle physics and cosmology, explaining, for example, why the pion as a bound quark-antiquark state is so much lighter than the three-quark proton. A hunt to create a pure Bose- Einstein condensate has been underway for over 15 years, with different groups employing different techniques to cool their bosons. The two recent successes have been achieved by incorporating several techniques. In both cases, the bosons have been atoms. In Colo just 2 arcsec away from the quasar. led to Einstein's prediction. Unlike rado, rubidium-87 was used, whilst at This tiny angular separation corre fermions, which obey the Pauli Rice University, the condensate was sponds to a distance 'on the ground' exclusion principle of only one formed from lithium-7. Both teams of 40,000 light-years. resident particle per allowed quantum started with the technique of laser There are strong indications that state, any number of bosons can cooling. This works by pointing finely this galaxy contains all the necessary pack into an identical quantum state. tuned laser beams at the sample nuclei to produce the observed This led Einstein to suggest that such that any atoms moving towards absorption effects. Only hydrogen under certain conditions, bosons a beam are struck by a photon, which and helium were produced in the Big would lose their individual identities, slows them down. -

Solid State Insurrection
INTRODUCTION WHAT IS SOLID STATE PHYSICS AND WHY DOES IT MATTER? Solid state physics sounds kind of funny. —GREGORY H. WANNIER, 1943 The Superconducting Super Collider (SSC), the largest scientific instrument ever proposed, was also one of the most controversial. The enormous parti- cle accelerator’s beam pipe would have encircled hundreds of square miles of Ellis County, Texas. It was designed to produce evidence for the last few elements of the standard model of particle physics, and many hoped it might generate unexpected discoveries that would lead beyond. Advocates billed the SSC as the logical apotheosis of physical research. Opponents raised their eyebrows at the facility’s astronomical price tag, which stood at $11.8 billion by the time Congress yanked its funding in 1993. Skeptics also objected to the reductionist rhetoric used to justify the project—which suggested that knowledge of the very small was the only knowledge that could be truly fun- damental—and grew exasperated when SSC boosters ascribed technological developments and medical advances to high energy physics that they thought more justly credited to other areas of science. To the chagrin of the SSC’s supporters, many such skeptics were fellow physicists. The most prominent among them was Philip W. Anderson, a No- bel Prize–winning theorist. Anderson had risen to prominence in the new field known as solid state physics after he joined the Bell Telephone Labora- tories in 1949, the ink on his Harvard University PhD still damp. In a House of Representatives committee hearing in July 1991, Anderson, by then at © 2018 University of Pittsburgh Press. -

A Modern View of the Equation of State in Nuclear and Neutron Star Matter
S S symmetry Article A Modern View of the Equation of State in Nuclear and Neutron Star Matter G. Fiorella Burgio * , Hans-Josef Schulze , Isaac Vidaña and Jin-Biao Wei INFN Sezione di Catania, Dipartimento di Fisica e Astronomia, Università di Catania, Via Santa Sofia 64, 95123 Catania, Italy; [email protected] (H.-J.S.); [email protected] (I.V.); [email protected] (J.-B.W.) * Correspondence: fi[email protected] Abstract: Background: We analyze several constraints on the nuclear equation of state (EOS) cur- rently available from neutron star (NS) observations and laboratory experiments and study the existence of possible correlations among properties of nuclear matter at saturation density with NS observables. Methods: We use a set of different models that include several phenomenological EOSs based on Skyrme and relativistic mean field models as well as microscopic calculations based on different many-body approaches, i.e., the (Dirac–)Brueckner–Hartree–Fock theories, Quantum Monte Carlo techniques, and the variational method. Results: We find that almost all the models considered are compatible with the laboratory constraints of the nuclear matter properties as well as with the +0.10 largest NS mass observed up to now, 2.14−0.09 M for the object PSR J0740+6620, and with the upper limit of the maximum mass of about 2.3–2.5 M deduced from the analysis of the GW170817 NS merger event. Conclusion: Our study shows that whereas no correlation exists between the tidal deformability and the value of the nuclear symmetry energy at saturation for any value of the NS mass, very weak correlations seem to exist with the derivative of the nuclear symmetry energy and with the nuclear incompressibility. -

Supersolid State of Matter Nikolai Prokof 'Ev University of Massachusetts - Amherst, [email protected]
University of Massachusetts Amherst ScholarWorks@UMass Amherst Physics Department Faculty Publication Series Physics 2005 Supersolid State of Matter Nikolai Prokof 'ev University of Massachusetts - Amherst, [email protected] Boris Svistunov University of Massachusetts - Amherst, [email protected] Follow this and additional works at: https://scholarworks.umass.edu/physics_faculty_pubs Part of the Physical Sciences and Mathematics Commons Recommended Citation Prokof'ev, Nikolai and Svistunov, Boris, "Supersolid State of Matter" (2005). Physics Review Letters. 1175. Retrieved from https://scholarworks.umass.edu/physics_faculty_pubs/1175 This Article is brought to you for free and open access by the Physics at ScholarWorks@UMass Amherst. It has been accepted for inclusion in Physics Department Faculty Publication Series by an authorized administrator of ScholarWorks@UMass Amherst. For more information, please contact [email protected]. On the Supersolid State of Matter Nikolay Prokof’ev and Boris Svistunov Department of Physics, University of Massachusetts, Amherst, MA 01003 and Russian Research Center “Kurchatov Institute”, 123182 Moscow We prove that the necessary condition for a solid to be also a superfluid is to have zero-point vacancies, or interstitial atoms, or both, as an integral part of the ground state. As a consequence, superfluidity is not possible in commensurate solids which break continuous translation symmetry. We discuss recent experiment by Kim and Chan [Nature, 427, 225 (2004)] in the context of this theorem, question its bulk supersolid interpretation, and offer an alternative explanation in terms of superfluid helium interfaces. PACS numbers: 67.40.-w, 67.80.-s, 05.30.-d Recent discovery by Kim and Chan [1, 2] that solid 4He theorem. -

Chapter 9 Phases of Nuclear Matter
Nuclear Science—A Guide to the Nuclear Science Wall Chart ©2018 Contemporary Physics Education Project (CPEP) Chapter 9 Phases of Nuclear Matter As we know, water (H2O) can exist as ice, liquid, or steam. At atmospheric pressure and at temperatures below the 0˚C freezing point, water takes the form of ice. Between 0˚C and 100˚C at atmospheric pressure, water is a liquid. Above the boiling point of 100˚C at atmospheric pressure, water becomes the gas that we call steam. We also know that we can raise the temperature of water by heating it— that is to say by adding energy. However, when water reaches its melting or boiling points, additional heating does not immediately lead to a temperature increase. Instead, we must overcome water's latent heats of fusion (80 kcal/kg, at the melting point) or vaporization (540 kcal/kg, at the boiling point). During the boiling process, as we add more heat more of the liquid water turns into steam. Even though heat is being added, the temperature stays at 100˚C. As long as some liquid water remains, the gas and liquid phases coexist at 100˚C. The temperature cannot rise until all of the liquid is converted to steam. This type of transition between two phases with latent heat and phase coexistence is called a “first order phase transition.” As we raise the pressure, the boiling temperature of water increases until it reaches a critical point at a pressure 218 times atmospheric pressure (22.1 Mpa) and a temperature of 374˚C is reached. -
![Arxiv:2012.04149V1 [Cond-Mat.Quant-Gas] 8 Dec 2020 Example, the Formation of Quantum Vortices When the System Is Enclosed in a Rotating Container](https://docslib.b-cdn.net/cover/7528/arxiv-2012-04149v1-cond-mat-quant-gas-8-dec-2020-example-the-formation-of-quantum-vortices-when-the-system-is-enclosed-in-a-rotating-container-1937528.webp)
Arxiv:2012.04149V1 [Cond-Mat.Quant-Gas] 8 Dec 2020 Example, the Formation of Quantum Vortices When the System Is Enclosed in a Rotating Container
Fermionic Superfluidity: From Cold Atoms to Neutron Stars Annette Lopez,1, 2 Patrick Kelly,1 Kaelyn Dauer,1 and Ettore Vitali1, 3 1Department of Physics, California State University Fresno, Fresno, California 93740 2Department of Physics, Brown University, Rhode Island 02912 3Department of Physics, The College of William and Mary, Williamsburg, Virginia 23187 From flow without dissipation of energy to the formation of vortices when placed within a rotating container, the superfluid state of matter has proven to be a very interesting physical phenomenon. Here we present the key mechanisms behind superfluidity in fermionic systems and apply our un- derstanding to an exotic system found deep within the universe|the superfluid found deep within a neutron star. A defining trait of a superfluid is the pairing gap, which the cooling curves of neu- tron stars depend on. The extreme conditions surrounding a neutron star prevent us from directly probing the superfluid’s properties, however, we can experimentally realize conditions resembling the interior through the use of cold atoms prepared in a laboratory and simulated on a computer. Experimentalists are becoming increasingly adept at realizing cold atomic systems in the lab that mimic the behavior of neutron stars and superconductors. In their turn, computational physicists are leveraging the power of supercomputers to simulate interacting atomic systems with unprece- dented accuracy. This paper is intended to provide a pedagogical introduction to the underlying concepts and the possibility of using cold atoms as a tool that can help us make significant strides towards understanding exotic physical systems. I. INTRODUCTION superfluidity, and in particular fermionic superfluidity, is described only in very advanced books and papers, which Moving from the \comfort zone" of classical mechanics makes it very hard for a student to have access to this to the more mysterious realm of quantum physics opens very beautiful chapter in physics. -

States of Matter
Educator Guide: States of Matter This document is a resource for teachers whose classes are participating in the Museum of Science’s States of Matter Program. The information in this document may be used as a classroom resource and/or as background information for the teacher concerning the subject of the states of matter. Table of Contents: Vocabulary List……………………………………………………………………………2 Further Background Reading…………………………………………………………...6 Suggested Classroom Materials……………………………………………………... 7 Activity Description………………………………………………………………………8 PowerPoint Description………………………………………………………………… 9 1 Vocabulary List This is a list of common terms that teachers may wish to be familiar with for the States of Matter program. This list is also a suggestion of vocabulary for students attending the program to learn, though prior study of these words is not required for student participation. Air – the collection of breathable gases that makes up the lower portion of the Earth’s atmosphere. The main components of air are Nitrogen (78%), Oxygen (21%), and other trace gases (1% ‐ Aragon, Carbon dioxide, Neon, Helium, etc…). Boiling – the transition from a liquid to a gas. Boiling is a much more energetic process than evaporation and happens throughout the liquid, not just at the surface. Boiling only occurs when a substance has reached its boiling point. Celsius – the unit of measurement for the most common temperature scale used throughout the world today. This is the temperature scale also used frequently by scientists.1 Condensing – the transition from a gas to a liquid. The temperature at which this change occurs is called the condensation point. Cryogenic Liquids – any liquid that exists at a really low temperature. -

Glossary of Terms In
Glossary of Terms in Powder and Bulk Technology Prepared by Lyn Bates ISBN 978-0-946637-12-6 The British Materials Handling Board Foreward. Bulk solids play a vital role in human society, permeating almost all industrial activities and dominating many. Bulk technology embraces many disciplines, yet does not fall within the domain of a specific professional activity such as mechanical or chemical engineering. It has emerged comparatively recently as a coherent subject with tools for quantifying flow related properties and the behaviour of solids in handling and process plant. The lack of recognition of the subject as an established format with monumental industrial implications has impeded education in the subject. Minuscule coverage is offered within most university syllabuses. This situation is reinforced by the acceptance of empirical maturity in some industries and the paucity of quality textbooks available to address its enormous scope and range of application. Industrial performance therefore suffers. The British Materials Handling Board perceived the need for a Glossary of Terms in Particle Technology as an introductory tool for non-specialists, newcomers and students in this subject. Co-incidentally, a draft of a Glossary of Terms in Particulate Solids was in compilation. This concept originated as a project of the Working Part for the Mechanics of Particulate Solids, in support of a web site initiative of the European Federation of Chemical Engineers. The Working Party decided to confine the glossary on the EFCE web site to terms relating to bulk storage, flow of loose solids and relevant powder testing. Lyn Bates*, the UK industrial representative to the WPMPS leading this Glossary task force, decided to extend this work to cover broader aspects of particle and bulk technology and the BMHB arranged to publish this document as a contribution to the dissemination of information in this important field of industrial activity. -

The Fourth State of Matter; an Introduction to Plasma Science
The Fourth State of Matter An Introduction to Plasma Science Second Edition Shalom Eliezer Plasma Physics Department Soreq Nuclear Research Center Yavne, Israel and Yaffa Eliezer Weizmann Institute of Science Rehovot, Israel Institute of Physics Publishing Bristol and Philadelphia IOP Publishing Ltd 2001 All rights reserved. No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without the prior permission of the publisher. Multiple copying is permitted in accordance with the terms of licences issued by the Copyright Licensing Agency under the terms of its agreement with the Committee of Vice-Chancellors and Principals. British Library Cataloguing-in-Publication Data A catalogue record of this book is available from the British Library. ISBN 0 7503 0740 4 Library of Congress Cataloging-in-Publication Data are available First edition 1989 Commissioning Editor: John Navas Production Editor: Simon Laurenson Production Control: Sarah Plenty Cover Design: Fre´de´rique Swist Marketing Executive: Colin Fenton Published by Institute of Physics Publishing, wholly owned by The Institute of Physics, London Institute of Physics Publishing, Dirac House, Temple Back, Bristol BS1 6BE, UK US Office: Institute of Physics Publishing, The Public Ledger Building, Suite 1035, 150 South Independence Mall West, Philadelphia, PA 19106, USA Typeset by Academic þ Technical, Bristol Printed in the UK by J W Arrowsmith Ltd, Bristol Dedication To our four children, Yosi, Lori, Orit and Dalya, their spouses and all our grandchildren. Where there is no vision, the people perish Book of Proverbs, Chapter 29, 18. -
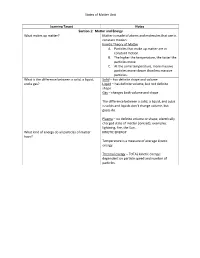
States of Matter Unit Learning Target Notes Section 1: Matter and Energy
States of Matter Unit Learning Target Notes Section 1: Matter and Energy What makes up matter? Matter is made of atoms and molecules that are in constant motion. Kinetic Theory of Matter A. Particles that make up matter are in constant motion. B. The higher the temperature, the faster the particles move. C. At the same temperature, more massive particles move slower than less massive particles. What is the difference between a solid, a liquid, Solid – has definite shape and volume and a gas? Liquid – has definite volume, but not definite shape Gas – changes both volume and shape The difference between a solid, a liquid, and a gas is solids and liquids don’t change volume, but gases do. Plasma – no definite volume or shape; electrically charged state of matter (ionized); examples: lightning, fire, the Sun… What kind of energy do all particles of matter KINETIC ENERGY have? Temperature is a measure of average kinetic energy. Thermal energy – TOTAL kinetic energy; dependent on particle speed and number of particles. States of Matter Unit Section 2: Changes of State What happens when a substance changes from The identity of the substance doesn’t change, but one state of matter to another? the energy of the substance does change. Freezing – Energy is released (liquid -> solid) Melting – Energy is absorbed (solid -> liquid) Condensation – Energy is released (gas -> liquid) Vaporization – Energy is absorbed (liquid -> gas) Sublimation – Energy is absorbed (solid -> gas) Deposition – Energy is released (gas -> solid) Temperature is constant during change of state. **You need to know the diagram at the bottom of page 84 What happens to mass and energy during physical Mass and energy are both conserved.