Low-Cost Microarchitectural Support for Improved Floating-Point Accuracy
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Intel® IA-64 Architecture Software Developer's Manual
Intel® IA-64 Architecture Software Developer’s Manual Volume 1: IA-64 Application Architecture Revision 1.1 July 2000 Document Number: 245317-002 THIS DOCUMENT IS PROVIDED “AS IS” WITH NO WARRANTIES WHATSOEVER, INCLUDING ANY WARRANTY OF MERCHANTABILITY, NONINFRINGEMENT, FITNESS FOR ANY PARTICULAR PURPOSE, OR ANY WARRANTY OTHERWISE ARISING OUT OF ANY PROPOSAL, SPECIFICATION OR SAMPLE. Information in this document is provided in connection with Intel products. No license, express or implied, by estoppel or otherwise, to any intellectual property rights is granted by this document. Except as provided in Intel's Terms and Conditions of Sale for such products, Intel assumes no liability whatsoever, and Intel disclaims any express or implied warranty, relating to sale and/or use of Intel products including liability or warranties relating to fitness for a particular purpose, merchantability, or infringement of any patent, copyright or other intellectual property right. Intel products are not intended for use in medical, life saving, or life sustaining applications. Intel may make changes to specifications and product descriptions at any time, without notice. Designers must not rely on the absence or characteristics of any features or instructions marked "reserved" or "undefined." Intel reserves these for future definition and shall have no responsibility whatsoever for conflicts or incompatibilities arising from future changes to them. Intel® IA-64 processors may contain design defects or errors known as errata which may cause the product to deviate from published specifications. Current characterized errata are available on request. Copies of documents which have an order number and are referenced in this document, or other Intel literature, may be obtained by calling 1-800- 548-4725, or by visiting Intel’s website at http://developer.intel.com/design/litcentr. -

Appendix D an Alternative to RISC: the Intel 80X86
D.1 Introduction D-2 D.2 80x86 Registers and Data Addressing Modes D-3 D.3 80x86 Integer Operations D-6 D.4 80x86 Floating-Point Operations D-10 D.5 80x86 Instruction Encoding D-12 D.6 Putting It All Together: Measurements of Instruction Set Usage D-14 D.7 Concluding Remarks D-20 D.8 Historical Perspective and References D-21 D An Alternative to RISC: The Intel 80x86 The x86 isn’t all that complex—it just doesn’t make a lot of sense. Mike Johnson Leader of 80x86 Design at AMD, Microprocessor Report (1994) © 2003 Elsevier Science (USA). All rights reserved. D-2 I Appendix D An Alternative to RISC: The Intel 80x86 D.1 Introduction MIPS was the vision of a single architect. The pieces of this architecture fit nicely together and the whole architecture can be described succinctly. Such is not the case of the 80x86: It is the product of several independent groups who evolved the architecture over 20 years, adding new features to the original instruction set as you might add clothing to a packed bag. Here are important 80x86 milestones: I 1978—The Intel 8086 architecture was announced as an assembly language– compatible extension of the then-successful Intel 8080, an 8-bit microproces- sor. The 8086 is a 16-bit architecture, with all internal registers 16 bits wide. Whereas the 8080 was a straightforward accumulator machine, the 8086 extended the architecture with additional registers. Because nearly every reg- ister has a dedicated use, the 8086 falls somewhere between an accumulator machine and a general-purpose register machine, and can fairly be called an extended accumulator machine. -
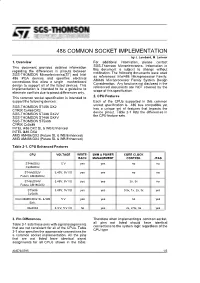
486 COMMON SOCKET IMPLEMENTATION by J
486 COMMON SOCKET IMPLEMENTATION by J. Lombard, M. Lerman 1. Overview For additional information, please contact This document provides detailed information SGS-Thomson Microelectronics. Information in this document is subject to change without regarding the differences in pinouts between notification. The following documents were used SGS-THOMSON Microelectronics(ST) and Intel as references: Intel486 Microprocessor Family, 486 PGA devices and specifies electrical connections that allow a single motherboard AM486 Microprocessor Family System Design Consideration. Any functions not disclosed in the design to support all of the listed devices. This referenced documents are NOT covered by the implementation is intended to be a guideline to scope of this specification. eliminate conflicts due to pinout differences only. 2. CPU Features This common socket specification is intended to support the following devices: Each of the CPUs supported in this common socket specification is 486 bus compatible yet SGS-THOMSON ST486 DX2 CYRIX Cx486 DX2 has a unique set of features that impacts the device pinout. Table 2-1 lists the differences in SGS-THOMSON ST486 DX2V the CPU feature sets. SGS-THOMSON ST486 DX4V SGS-THOMSON ST5x86 CYRIX Cx5x86 INTEL i486 DX2 SL & WB Enhanced INTEL i486 DX4 AMD AM486 DX2 (Future SL & WB Enhanced) AMD AM486 DX4 (Future SL & WB Enhanced) Table 2-1. CPU Enhanced Features CPU VOLTAGE WRITE- SMM & POWER CORE CLOCK BACK MANAGEMENT CONTROL JTAG ST486DX2 5 V yes yes no no Cx486DX2 ST486DX2V 3.45V, 5V I/O yes yes no no Future AM486DX2 ST486DX4V 3.45V, 5V I/O yes yes 2x, 3x no Future AM486DX2 ST5x86 3.45V, 5V I/O yes yes 0.5x, 1x, 2x, 3x yes Cx5x86 Intel i486DX/DX2 SL & WB 5 V yes yes no yes Enh. -

MICROPROCESSOR REPORT the INSIDERS’ GUIDE to MICROPROCESSOR HARDWARE Slot Vs
VOLUME 12, NUMBER 1 JANUARY 26, 1998 MICROPROCESSOR REPORT THE INSIDERS’ GUIDE TO MICROPROCESSOR HARDWARE Slot vs. Socket Battle Heats Up Intel Prepares for Transition as Competitors Boost Socket 7 A A look Look by Michael Slater ship as many parts as they hoped, especially at the highest backBack clock speeds where profits are much greater. The past year has brought a great deal The shift to 0.25-micron technology will be central to of change to the x86 microprocessor 1998’s CPU developments. Intel began shipping 0.25-micron A market, with Intel, AMD, and Cyrix processors in 3Q97; AMD followed late in 1997, IDT plans to LookA look replacing virtually their entire product join in by mid-98, and Cyrix expects to catch up in 3Q98. Ahead ahead lines with new devices. But despite high The more advanced process technology will cut power con- hopes, AMD and Cyrix struggled in vain for profits. The sumption, allowing sixth-generation CPUs to be used in financial contrast is stark: in 1997, Intel earned a record notebook systems. The smaller die sizes will enable higher $6.9 billion in net profit, while AMD lost $21 million for the production volumes and make it possible to integrate an L2 year and Cyrix lost $6 million in the six months before it was cache on the CPU chip. acquired by National. New entrant IDT added another com- The processors from Intel’s challengers have lagged in petitor to the mix but hasn’t shipped enough products to floating-point and MMX performance, which the vendors become a significant force. -

Extensions to Instruction Sets
Extensions to Instruction Sets Ricardo Manuel Meira Ferrão Luis Departamento de Informática, Universidade do Minho 4710 - 057 Braga, Portugal [email protected] Abstract. This communication analyses extensions to instruction sets in general purpose processors, together with their evolution and significant innovation. It begins with an overview of specific multimedia and digital signal processing requirements and then it focuses on feature detection to properly identify the adequate extension. A brief performance evaluation on two competitive processors closes the communication. 1 Introduction The purpose of this communication is to analyse extensions to instruction sets, describe the specific multimedia and digital signal processing (DSP) requirements of a processor, detail how to detect these extensions and verify if the processor supports them. To achieve this functionality an IA32 architecture example code will be demonstrated. To study the instruction sets supported by each processor, an analysis is performed to compare and distinguish each technology in terms of new extensions to instruction sets and architecture evolution, mapping a table that lists the instruction sets supported by each processor. To clearly identify these differences between architectures, tests are performed with an application example, determining comparable results of two competitive processors. In this communication, Section 2 gives an overview of multimedia and digital signal processing requirements, Section 3 explains the feature detection of these instructions, Section 4 details some of the extensions supported by IA32 based processors, Section 5 tests and describes the performance of each technology and analyses the results. Section 6 concludes this communication. 2 Multimedia and DSP Requirements Computer industries needed a way to improve their multimedia capabilities because of the demand for 3D graphics, video and other multimedia applications such as games. -

Communication Theory II
Microprocessor (COM 9323) Lecture 2: Review on Intel Family Ahmed Elnakib, PhD Assistant Professor, Mansoura University, Egypt Feb 17th, 2016 1 Text Book/References Textbook: 1. The Intel Microprocessors, Architecture, Programming and Interfacing, 8th edition, Barry B. Brey, Prentice Hall, 2009 2. Assembly Language for x86 processors, 6th edition, K. R. Irvine, Prentice Hall, 2011 References: 1. Computer Architecture: A Quantitative Approach, 5th edition, J. Hennessy, D. Patterson, Elsevier, 2012. 2. The 80x86 Family, Design, Programming and Interfacing, 3rd edition, Prentice Hall, 2002 3. The 80x86 IBM PC and Compatible Computers, Assembly Language, Design, and Interfacing, 4th edition, M.A. Mazidi and J.G. Mazidi, Prentice Hall, 2003 2 Lecture Objectives 1. Provide an overview of the various 80X86 and Pentium family members 2. Define the contents of the memory system in the personal computer 3. Convert between binary, decimal, and hexadecimal numbers 4. Differentiate and represent numeric and alphabetic information as integers, floating-point, BCD, and ASCII data 5. Understand basic computer terminology (bit, byte, data, real memory system, protected mode memory system, Windows, DOS, I/O) 3 Brief History of the Computers o1946 The first generation of Computer ENIAC (Electrical and Numerical Integrator and Calculator) was started to be used based on the vacuum tube technology, University of Pennsylvania o1970s entire CPU was put in a single chip. (1971 the first microprocessor of Intel 4004 (4-bit data bus and 2300 transistors and 45 instructions) 4 Brief History of the Computers (cont’d) oLate 1970s Intel 8080/85 appeared with 8-bit data bus and 16-bit address bus and used from traffic light controllers to homemade computers (8085: 246 instruction set, RISC*) o1981 First PC was introduced by IBM with Intel 8088 (CISC**: over 20,000 instructions) microprocessor oMotorola emerged with 6800. -

Programmable Digital Microcircuits - a Survey with Examples of Use
- 237 - PROGRAMMABLE DIGITAL MICROCIRCUITS - A SURVEY WITH EXAMPLES OF USE C. Verkerk CERN, Geneva, Switzerland 1. Introduction For most readers the title of these lecture notes will evoke microprocessors. The fixed instruction set microprocessors are however not the only programmable digital mi• crocircuits and, although a number of pages will be dedicated to them, the aim of these notes is also to draw attention to other useful microcircuits. A complete survey of programmable circuits would fill several books and a selection had therefore to be made. The choice has rather been to treat a variety of devices than to give an in- depth treatment of a particular circuit. The selected devices have all found useful ap• plications in high-energy physics, or hold promise for future use. The microprocessor is very young : just over eleven years. An advertisement, an• nouncing a new era of integrated electronics, and which appeared in the November 15, 1971 issue of Electronics News, is generally considered its birth-certificate. The adver• tisement was for the Intel 4004 and its three support chips. The history leading to this announcement merits to be recalled. Intel, then a very young company, was working on the design of a chip-set for a high-performance calculator, for and in collaboration with a Japanese firm, Busicom. One of the Intel engineers found the Busicom design of 9 different chips too complicated and tried to find a more general and programmable solu• tion. His design, the 4004 microprocessor, was finally adapted by Busicom, and after further négociation, Intel acquired marketing rights for its new invention. -

Intel Prepares MMX CPU Wave After Weak 1996, AMD and Cyrix Ready 1997 Counterstrike
MICRODESIGN R ESOURCES SPECIAL REPORT Intel Prepares MMX CPU Wave After Weak 1996, AMD and Cyrix Ready 1997 Counterstrike by Michael Slater Nineteen ninety six was a remarkably successful one for Intel and a difficult one for its competitors. It was a quiet year for Intel in terms of new products, but the company nevertheless increased both its market share and its gross margin—thanks, in large part, to weak performances from AMD and Cyrix. (See list on page 14 for a summary of the key events of 1996 and pointers to Microprocessor Report’s coverage.) This year promises to be far more turbulent. Not only is Intel intro- ducing two major new product lines—P55C (officially, Pentium Processor with MMX Technology) and Klamath—but AMD and Cyrix will each launch their own next-generation processors, which will be more formi- dable competitors to Intel’s line. Intel is sure to do well despite the stepped-up challenge, but its dominance of the market is unlikely to be quite as complete in 1997 as in 1996. Intel Shifting into In 1996, Intel’s microprocessor lineup changed little. After the introduction High Gear of the 150- and 166-MHz Pentiums in January, the only new products were the 200-MHz Pentium and 150-MHz Mobile Pentium. The P55C would have been a great kicker for fall sales, but Intel apparently didn’t have the part ready in time. Intel began producing P55C processors in the late fall but chose not to announce the part until January in order to minimize the impact on the Christmas selling season. -

APPLICATION NOTE Ap·113
APPLICATION Ap·113 NOTE February 1981 Intel Corporation makes no warranty for the use of its products and assumes no responsibility for any errors which may appear in this document nor does it make a commitment to update the information contained herein. Intel software products are copyrighted by and shall remain the property of Intel Corporation. Use, duplication or disclosure is subjectto restrictions stated in Intel's software license, or as defined in ASPR 7-104.9 (a) (9). Intel Corporation a!=;sumes no resDonsibilitv for the use of anv circuitry other than circuitry embodied in an Intel product. No other circuit patent licenses are implied. No part of this document may be copied or reproduced in any form or by any means without the prior written consent of Intel Corporation. The following are trademarks of Intel Corporation and may only be used to identify Intel products: BXP Intelevision MULTIBUS* CREDIT Intellec MULTIMODULE i iSBC Plug-A-Bubble ICE iSBX PROMPT ICS Library Manager Promware im MCS RMX Insite Megachassis UPI Intel Micromap ~Scope System 2000 and the combinations of ICE, iCS, iSBC, MCS or RMX and a numerical suffix. MDS is an ordering code only and is not used as a product name or trademark. MDS® is a registered trademark of Mohawk Data Sciences Corporation. *MULTIBUS is a patented Intel bus. Additional copies of this manual or other Intel literature may be obtained from: Intel Corporation Literature Department SV3-3 3065 Bowers Avenue Santa Clara, CA 95051 © INTEL CORPORATION, 1981 AFN-013008-1 Ap·113 Getting Started With Contents the Numeric Data INTRODUCTION Processor iAPX 86,88 Base ............................. -

Introduction to Cpu
microprocessors and microcontrollers - sadri 1 INTRODUCTION TO CPU Mohammad Sadegh Sadri Session 2 Microprocessor Course Isfahan University of Technology Sep., Oct., 2010 microprocessors and microcontrollers - sadri 2 Agenda • Review of the first session • A tour of silicon world! • Basic definition of CPU • Von Neumann Architecture • Example: Basic ARM7 Architecture • A brief detailed explanation of ARM7 Architecture • Hardvard Architecture • Example: TMS320C25 DSP microprocessors and microcontrollers - sadri 3 Agenda (2) • History of CPUs • 4004 • TMS1000 • 8080 • Z80 • Am2901 • 8051 • PIC16 microprocessors and microcontrollers - sadri 4 Von Neumann Architecture • Same Memory • Program • Data • Single Bus microprocessors and microcontrollers - sadri 5 Sample : ARM7T CPU microprocessors and microcontrollers - sadri 6 Harvard Architecture • Separate memories for program and data microprocessors and microcontrollers - sadri 7 TMS320C25 DSP microprocessors and microcontrollers - sadri 8 Silicon Market Revenue Rank Rank Country of 2009/2008 Company (million Market share 2009 2008 origin changes $ USD) Intel 11 USA 32 410 -4.0% 14.1% Corporation Samsung 22 South Korea 17 496 +3.5% 7.6% Electronics Toshiba 33Semiconduc Japan 10 319 -6.9% 4.5% tors Texas 44 USA 9 617 -12.6% 4.2% Instruments STMicroelec 55 FranceItaly 8 510 -17.6% 3.7% tronics 68Qualcomm USA 6 409 -1.1% 2.8% 79Hynix South Korea 6 246 +3.7% 2.7% 812AMD USA 5 207 -4.6% 2.3% Renesas 96 Japan 5 153 -26.6% 2.2% Technology 10 7 Sony Japan 4 468 -35.7% 1.9% microprocessors and microcontrollers -

IDT Winchip 2A Data Sheet
Preliminary Information PROCESSOR Version A Data Sheet Preliminary Information January 1999 IDT WINCHIP 2ATM PROCESSOR DATA SHEET This is Version 1.0 of the IDT WinChip 2 version A Processor data sheet. The latest versions of this data sheet may be obtained from www.winchip.com © 1999 Integrated Device Technology, Inc. All Rights Reserved Integrated Device Technology, Inc. (IDT) reserves the right to make changes in its products without notice in order to improve design or performance characteristics. This publication neither states nor implies any representations or warranties of any kind, including but not limited to any implied warranty of merchantability or fitness for a particular purpose. No license, express or implied, to any intellectual property rights is granted by this document. IDT makes no representations or warranties with respect to the accuracy or completeness of the contents of this publication or the information contained herein, and reserves the right to make changes at any time, without notice. IDT disclaims responsibility for any consequences resulting from the use of the information included herein. LIFE SUPPORT POLICY Integrated Device Technology's products are not authorized for use as components in life support or other medical devices or systems (hereinafter life support devices) unless a specific written agreement pertaining to such intended use is executed between the manufacturer and an officer of IDT. 1. Life support devices are devices which (a) are intended for surgical implant into the body or (b) support or sustain life and whose failure to perform, when properly used in accordance with instructions for use provided in the labeling, can be reasonably expected to result in a significant injury to the user. -

Computer Architectures an Overview
Computer Architectures An Overview PDF generated using the open source mwlib toolkit. See http://code.pediapress.com/ for more information. PDF generated at: Sat, 25 Feb 2012 22:35:32 UTC Contents Articles Microarchitecture 1 x86 7 PowerPC 23 IBM POWER 33 MIPS architecture 39 SPARC 57 ARM architecture 65 DEC Alpha 80 AlphaStation 92 AlphaServer 95 Very long instruction word 103 Instruction-level parallelism 107 Explicitly parallel instruction computing 108 References Article Sources and Contributors 111 Image Sources, Licenses and Contributors 113 Article Licenses License 114 Microarchitecture 1 Microarchitecture In computer engineering, microarchitecture (sometimes abbreviated to µarch or uarch), also called computer organization, is the way a given instruction set architecture (ISA) is implemented on a processor. A given ISA may be implemented with different microarchitectures.[1] Implementations might vary due to different goals of a given design or due to shifts in technology.[2] Computer architecture is the combination of microarchitecture and instruction set design. Relation to instruction set architecture The ISA is roughly the same as the programming model of a processor as seen by an assembly language programmer or compiler writer. The ISA includes the execution model, processor registers, address and data formats among other things. The Intel Core microarchitecture microarchitecture includes the constituent parts of the processor and how these interconnect and interoperate to implement the ISA. The microarchitecture of a machine is usually represented as (more or less detailed) diagrams that describe the interconnections of the various microarchitectural elements of the machine, which may be everything from single gates and registers, to complete arithmetic logic units (ALU)s and even larger elements.