DOCSLIB.ORG

Ic-23 Optimization of a Rolling And

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Ic-23 Optimization of a Rolling And Joint International Conference on Computing and Decision Making in Civil and Building Engineering June 14-16, 2006 - Montréal, Canada OPTIMIZATION OF A ROLLING AND FLOATING LOCK GATE FOR THE ANTWERP PORT T. Richir1, J.-P. Pecque 2, C. Toderan3, F. Bair4 and P. Rigo5 ABSTRACT The Antwerp port authority recently decided to convert one of its shipping locks into a dedicated inland navigation lock to improve the traffic between the port and the Scheldt River. The rolling gate, considered for this lock, has to float to be led into the port for maintenance and repairing operations. Two partitioned floating tanks are used inside the gate. Water ballast can be pumped from the floating tanks to float the structure or to restore the mass equilibrium in case of damage due to ship impact. This paper presents a methodology to minimi e the weight of the gate by optimi ing simultaneously the height of the floating tanks, the number of their watertight partitions and the gate scantling while considering the floating stability (Pecquet 2005). KE, WORDS multi-ob(ective optimi ation, LBR-5 software, floating lock gate INTROD-CTION Antwerp (Belgium) is less than 100 km away from the embouchure of the Scheldt River into the ,orth Sea so that the Scheldt River is there still sensitive to the tides. To keep a constant water level inside the Antwerp port, seven shipping locks are used (-igure 1). The Antwerp port authority recently decided to convert one of these shipping locks (the .an Cauwelaert lock) into a dedicated inland navigation lock to improve the traffic between the port and the Scheldt River. A rolling gate, so-called 0wheelbarrow1 or 0lateral displacement gate1 (P2A,C 1385), is considered for this lock (-igure 2). 2ts dimensions are 35 7 8 7 13 m (length 7 width 7 height). 9oreover this gate has to float to be led into the port for maintenance and repairing operations. Two partitioned floating tanks are thus used inside the gate. Water ballast can be pumped from the floating tanks to float the structure or to restore the mass equilibrium in 1 Ph.D. Student, -.R.2.A. Scholarship, A,AST, University of Liege, Bat. B52/3, Chemin des Chevreuils 1, B-4000 Liege, Belgium, Phone +32-4-3554853, -a7 +32-4-3553133, thomas.richir? ulg.ac.be 2 Pro(ect Engineer, Study and Engineering Affice, SBE, Slachthuisstraat 81, B-3100 Sint-,iklaas, Belgium, Phone +32-3-8883513, -a7 +32-3-8883883, (p.pecquet? sbe.be 3 Research Engineer, A,AST, University of Liege, Bat. B52/3, Chemin des Chevreuils 1, B-4000 Liege, Belgium, Phone +32-4-3553341, -a7 +32-4-3553133, catalin.toderan? ulg.ac.be 4 Research Engineer, A,AST, University of Liege, Bat. B52/3, Chemin des Chevreuils 1, B-4000 Liege, Belgium, Phone +32-4-3553521, -a7 +32-4-3553133, f.bair? ulg.ac.be 5 Professor, -.,.R.S. Research Director, A,AST, University of Liege, Bat. B52/3, Chemin des Chevreuils 1, B-4000 Liege, Belgium, Phone +32-4-3553355, -a7 +32-4-3553133, ph.rigo? ulg.ac.be Page 155 Joint International Conference on Computing and Decision Making in Civil and Building Engineering June 14-16, 2006 - Montréal, Canada case of damage due to ship impact. Solid ballast is placed at the bottom of the gate to ensure floating stability. Dandvliet lock Berendrecht lock Baudewi(n lock .an Cauwelaer loc1 Eallo lock Royens lock Eattendi(k lock -igure 1: 2mplantation of the Shipping Locks of the Antwerp Port E7ceptional high tide level Usual level PORT OF ANTWERP 3.00 m Constant level 4.50 m 13.13 m E7ceptional low tide level 1 Abservation tube 2 2 2 -loating tanks 1 12.34 m SCHELDT RI.ER 3 Water ballast 3 3 4 Solid ballast 10.13 m 4 1.00 m 8.12 m -igure 2: Cross-Section of the .an Cauwelaert Lock Cate Page 156 Joint International Conference on Computing and Decision Making in Civil and Building Engineering June 14-16, 2006 - Montréal, Canada The floating stability analysis of the gate is e7plained in the first part of the paper. The LBR-5 software (Rigo 2001a, Rigo 2001b, Rigo 2003) used to optimi e the gate scantling is described in the second part. The third part presents the way to minimi e the weight of the gate by optimi ing simultaneously the height of the floating tanks, the number of their watertight partitions and the gate scantlings while considering the floating stability. FLOATING STABILIT, The rolling gate considered for the .an Cauwelaert lock has to float to be led into the port for maintenance or repairing operations. 9oreover the gate has still to float with a ma7imum 8 m wide hole in one floating tank caused by a boat impact. WATER BALLAST Two partitioned floating tanks are filled partially with water ballast which can be pumped out to float the structure and to restore the mass equilibrium in case of damage. The minimum height of water ballast is thus given by -igure 3 and Equations 1 to 4: L F 35.43 m B F 8.12 m Ht Hwb Lp BOAT B F 8.12 m Bb F 8.00 m Li (a) (b) -igure 3: E7ample for Damaged -loating Tanks (a) Plan .iew (b) Cross-Section .olume of income water: .i F B/2 7 (Ht H Hwb) 7 Li I1J .olume of water ballast to pump out: .o F B/2 7 Hwb 7 (L H Li) I2J Water ballast height (I1J F I2J): Hw2 3 H 4 Li 5 L I3J Length of income water: Li F Kroundup (Bb / Lp) + 1L 7 Lp I4J with Lp distance between two transverse watertight partitions Ht height of the floating tanks SOLID BALLAST The floating stability is assessed through the metacentric height, which is given by Equation 5: GM = KB + BM − KG − ∆GM I5J with C9 metacentric height Page 157 Joint International Conference on Computing and Decision Making in Civil and Building Engineering June 14-16, 2006 - Montréal, Canada E* distance between the gate bottom (E) and the buoyancy center (B) EC distance between the gate bottom (E) and the gravity center (C) BM metacentric radius F 2T / ∇ where 2T water plane moment of inertia ∇ under water volume (displacement) ∆C9 0free surface effect1 due to water ballast F i / ∇ where i free surface moment of inertia The role of solid ballast is to lower the gravity center and thus to increase the metacentric height. 2n case of damage the mass equilibrium is restored by pumping out water ballast but the gravity center goes up so that the metacentric height decreases. The minimum height of solid ballast is thus given by Equation 5 in case of damage and by considering a minimum 40 cm metacentric height as floating stability condition. The considered density of solid ballast is 80 k,/mM (steel blocks). SCANTLING OPTIMIZATION The .an Cauwelaert lock gate is composed by steel stiffened plates. A least weight optimi ation of the gate scantling (profile si es, dimensions and spacing) can be performed with the LBR-5 software (Rigo 2001a, Rigo 2001b, Rigo 2003). LBR-5 SOFTWARE Structural design is always defined during the earliest phases of a pro(ect. 2t is thus not difficult to understand why a preliminary design stage optimi ation tool is attractive. This is precisely the way the LBR-5 optimi ation software for stiffened structures was conceptuali ed. LBR-5 is an integrated package to analy e and optimi e naval and hydraulic structures at their earliest stages: tendering and preliminary design. 2nitial scantling is not mandatory. Designers can start directly with an automatic search for optimum si ing (scantling). Design variables (plate thicknesses, stiffener dimensions and spacing) are freely selected by the user. LBR-5 is composed of 3 basic modules (APT2, CA,STRA2,T and CAST). The user selects the relevant constraints (geometrical and structural constraints) in e7ternal databases. When the optimi ation deals with least construction costs, unitary material, welding, cutting and labor costs must be specified by the user to define an e7plicit ob(ective function (not empirical). -or least weight, these unitary costs are not used and the ob(ective function depends only on the geometrical parameters. Using all these data (constraints, ob(ective function and sensitivity analysis), the optimum solution is found using an optimi ation algorithm based on conve7 lineari ations and a dual approach (-leury 1383, Rigo and -leury 2001). 2ndependent of the number of design variables and constraints, the number of iterations requiring a complete structural re-analysis is limited to 10 or 15. MODELLING DESCRIPTION The LBR-5 mesh model (-igure 4) of the .an Cauwelaert lock gate includes: • 25 stiffened panels with 3 design variables each, i.e.: Page 158 Joint International Conference on Computing and Decision Making in Civil and Building Engineering June 14-16, 2006 - Montréal, Canada o Plate thickness o -or longitudinal stiffeners and transverse frames: ° Web height and thickness ° -lange width ° Spacing • 155 design variables (some design variables of stiffened panels are not considered) • 35 equality constraints, e.g. to impose uniform frames spacing and transverse symmetry • 213 geometrical constraints • 1400 structural constraints (280 per loading case), such as: o Plate yielding (.on 9ises) o Stiffener yielding (web and flange) o -rame yielding (web and flange) o Stiffener ultimate strength • 1 constraint imposing the gravity center cannot go up during the optimi ation process 1 6 6 13 6 2 12 23 24 25 (a) 3 6 6 6 6 11 6 6 4 10 18 13 6 6 6 5 22 3 (b) 20 21 6 6 6 5 8 8 14 6 6 15 15 6 6 18 -igure 4: LBR-5 9odelling (a) 9esh 9odel of the .an Cauwelaert Lock Cate (b) Stiffened Panel Element -ive loading cases are considered during the optimi ation process: • Three different levels of the Scheldt River (-igure 2), • Emptying of the port when the Scheldt River is at the average level, • 240 k,/mN test pressure in each floating tank when the gate is not yet in the water.
Load more

Recommended publications
  • Controlling Se Iment Accumulation Behind He Locks of Zandvliet and Be En Rech
    CONTROLLING SE IMENT ACCUMULATION BEHIND HE LOCKS OF ZANDVLIET AND BE EN RECH by Edward De Broe Head of the Dredging Department, Port Authority of Antwerp. 20, Siberiastreet, quay 63, B-2030 Antwerp (Belgium). E-mail: [email protected] Fax: 03/205.24.37. Key words The lower Scheldt is that part of the Scheldt from the roadstead of Antwerp to the Dutch border. Sediment Antwerp, Scheldt, docks, sedimentation pattern, reaches the lower Scheldt from upstream as well as measurement campaign, siltation downstream. The silt tends preferably to settle in the access channels to the locks. Sedimentation-rates of 100 to 350 kg d.s./m2/month (d.s.: dry sediment) were Mots-clefs measured. The lower Scheldt can, in this respect, be regarded as a huge silt reservoir of unconsolidated silt. Anvers, Escaut, dock, modalites de sedimentation, The access channel to the Zandvliet and Berendrecht acquisition de donnees, envasement locks has a surface area of 60 ha and computations proved the quasi-permanent presence of an unconsol­ 1. DESCRI TION OF idated silt volume of about 2 million m3. THE SEDIMENT SUPPLY Past measurements to identify the sedimentation mechanism at work in the access channel to the locks MECHANISM FROM proved the existence of density flows of salt water laden with silt. The presence of this saline wedge is THE RIVER SCHELDT most emphatic at high tide. The density flows, which are driven by small differences of salinity, may be TO THE DOCKS reinforced by differences in suspension concentra­ tions and a difference in temperature. Presumably, the same mechanism is at work during lock opera­ tions due to the contact between imushing water of 1.1 Analysis of historical an average salinity which is always greater than the data one of the less brackish water in the docks.
    [Show full text]
  • National Activities 2013
    NATIONAL ACTIVITIES 2013 Traditionally the PIANC-AIPCN. Belgium Young Professionals started their year 2013 on January 17 with a culinary road trip. This time organized in Brussels, on which 15 gourmands participated. On March 26 2013, the annual general assembly of PIANC-AIPCN. Belgium took place. About 92 members participated in the assembly. This year, it was the Brussels region that organised the annual meeting in the neighbourhood of the Port of Brussels, on a place where you can still find the ancient warehouses and sheds. The assembly itself took place in one of the marvellous old wine cellars of the port. Ancient warehouses and sheds General assembly in the old wine cellers During the statutory part of the assembly, three new board members were appointed: ir. Freddy Aerts (Flemish authority), prof. dr. ir. Peter Troch (UGhent) and ir. Jean Polet (Besix) in replacement of ir. Luc Van Damme, prof. dr. ir. Julien De Rouck and ir. Jules Janssen. Ir. L. Van Damme, now retired, was appointed as treasurer of PIANC-AIPCN.be. During the academic part of the assembly, interesting presentations about the foundation and the construction of the Up-site-project, bordering the ABC canal were presented. Up-site building the new landmark of Brussels-North. Up-site building Port of Brussels from the top of the tower Tour & Taxis Top-information to the PIANC group The lunch was served in the Royal Depot of Tour & Taxis. Afterwards a numerous part of the PIANC members took the opportunity to climb up the highest residence tower in Brussels (140 m high), still in construction.
    [Show full text]
  • Data Analysis Water Levels Bath Lower Sea Scheldt
    Werkgroep O&M - Projectgroep Veiligheid SUB PROJECT 1: DATA ANALYSIS AND HYPOTHESIS - LOWER SEA SCHELDT 756_05 WL Rapporten Werkgroep O&M - Projectgroep Veiligheid Sub project 1: Data analysis and hypothesis - Lower Sea Scheldt Plancke, Y.; Maximova, T.; Ides, S.; Peeters, P.; Taverniers, E.; Mostaert, F. April 2012 WL2012R756_05_rev4_0 FORM: F-WL-PP10-2 Version 02 VALID AS FROM: 17/04/2009 This publication must be cited as follows: Plancke, Y.; Maximova, T.; Ides, S.; Peeters, P.; Taverniers, E.; Mostaert, F. (2012). Werkgroep O&M - Projectgroep Veiligheid: Sub project 1: Data analysis and hypothesis - Lower Sea Scheldt. Version 4.0. WL Rapporten, 756/05. Flanders Hydraulics Research: Antwerp, Belgium Waterbouwkundig Laboratorium Flanders Hydraulics Research Berchemlei 115 B-2140 Antwerp Tel. +32 (0)3 224 60 35 Fax +32 (0)3 224 60 36 E-mail: [email protected] www.watlab.be Nothing from this publication may be duplicated and/or published by means of print, photocopy, microfilm or otherwise, without the written consent of the publisher. FORM: F-WL-PP10-2 Version 02 VALID AS FROM: 17/04/2009 Document identification Werkgroep O&M - Projectgroep Veiligheid: Sub project 1: Data analysis and hypothesis - Title: Lower Sea Scheldt Werkgroep O&M - Projectgroep Customer: Ref.: WL2012R756_05_rev4_0 Veiligheid Keywords (3-5): Tides, morphology, Sea Scheldt, historical evolution Text (p.): 49 Tables (p.): 1 Appendices (p.): / Figures (p.): / Yes Customer Exceptions: Internal Confidentiality: Flemish government Released as from No Available online Approval Author Reviser Project leader Division Head Ir. Yves Plancke Ir. Eric Taverniers Ir. Patrik Peeters Dr. Frank Mostaert Ir. Tatiana Maximova Revisions Nr.
    [Show full text]
  • The Panama Canal
    www.PDHcenter.com www.PDHonline.org Table of Contents Slide/s Part Description 1N/ATitle The 2 N/A Table of Contents 3~41 1 A Place of Many Fishes 42~172 2 The French Era Pana 173~372 3 Essayons 373~547 4 Gatun 548~631 5 Making the Cut ma 632~680 6 On to the Pacific 681~722 7 A Path Between the Seas 723~823 8 Strategically & Otherwise 824~853 9 Something Must Be Done Canal 854~900 10 A Canal for the 21st Century A Land Divided, A World1 2 United In1494–twoyearsafterhe set out for the East-Indies by sailing westward, master mariner and navigator Cristobol Colon (a.k.a. Part 1 Christopher Columbus), in service to the Spanish crown, announced his discovery of a “New World.” His four voyages (1492– A Place of Many Fishes 1493, 1493–1496, 1498–1500 and 1502–1504) would open the way for European exploration, exploitation, and colonization. 3 4 “…On September 25, 1513, Vasco Nunez de Balboa “…From where Balboa stood his new ocean lay directly climbed the peaks of the Continental Divide and south, because of the S-shaped twist of the Isthmus…When discovered the Pacific Balboa’s report of his discovery reached Spain, it was Ocean, which he named ‘The accompanied by the recommendation that a canal be South Sea…’” immediately dug across the Isthmus. What the explorer had Popular Mechanics, Dec. 1913 RE: the idea of digging a water in mind was a sea-level canal, for although Leonardo Da passage across the Isthmus of Vinci, the great Italian painter-engineer, had recently invented Panama to connect the Atlantic the hydraulic lock now generally used for lifting vessels over and PifiPacific O/Ocean/s emerged in the early 16th century, when elevations, it had not become widely known.
    [Show full text]
  • Tariff Regulations for Inland Shipping
    Tariff regulations for inland shipping FREE TRANSLATION – Only the Dutch version is legally valid Antwerp Port Authority www.portofantwerp.com Board of Directors of the 10th of December 2018 Date of commencement : 1st of January 2019 Index Basic principles .................................................................................................................. 6 ARTICLE 1 Nomenclature ......................................................................................... 6 1.1 Dredging vessels ............................................................................................ 6 1.2 Destination ..................................................................................................... 6 1.3 Inland shipping dues ...................................................................................... 6 1.4 Inland vessels ................................................................................................. 6 1.5 Bunker vessels ............................................................................................... 6 1.6 Bunker vessels type N ................................................................................... 6 1.7 Container ships .............................................................................................. 7 1.8 Passage fee .................................................................................................... 7 1.9 Push barges .................................................................................................... 7 1.10 Pushers ..........................................................................................................
    [Show full text]
  • PIANC Workshop: What's New in the Design of Navigation Locks?
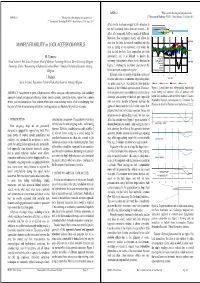
    PAPER 6-2 “What’s new in the design of navigation locks” nd PAPER 6-2 “What’s new in the design of navigation locks” 2 International Workshop, PIANC – New-Orleans, 13-14 Sept. 2011 2nd International Workshop, PIANC – New-Orleans, 13-14 Sept. 2011 effect similar to a bank or quay wall – attraction to the wall combined with a bow-out moment – the + effect of a permeable wall is completely different. Moreover, flow asymmetry clearly still affects the ship after the latter has entered completely into the repulsion MANEUVERABILITY in LOCK ACCESS CHANNELS lock or, during an exit maneuver, even before the ship has left the lock. Lock approaches are often asymmetric, and it is difficult to predict the M. Vantorre 12000 TEU occurring hydrodynamic effects; this is illustrated in Centric approach attraction Naval Architect, Full Senior Professor, Head of Maritime Technology Division, Ghent University, Belgium Dead slow Figure 2, showing the oscillatory character of the 2 knots Knowledge Centre ‘Maneuvering in Shallow & Confined Water’, Flanders Hydraulics Research, Antwerp, 20% UKC Belgium forces acting on an approaching ship. No density exchange Although locks are mostly planned in a protected -1.5 -1 -0.5 0 0.5 1 1.5 J. Richter location with respect to currents, approaching ships Position [Lpp] Naval Architect, Researcher, Flanders Hydraulics Research, Antwerp, Belgium are quite sensitive to even moderate flow patterns no wall permeable wall closed wall 'invisible' wall because of their limited approach speed. Moreover, Figure 1. Lateral force on a self-propelled guided ship ABSTRACT: An overview is given of hydrodynamic effects acting on a ship approaching a lock, including lock operations may cause additional currents due to model during lock approach: effect of approach wall approach channel and approach structure layout, density currents, translation waves, return flow, cushion discharge and opening of the lock gate; especially layout.
    [Show full text]
  • Investment Guide
    Investment guide The port of Antwerp, an international integrated platform ith this investment guide we seek to support you W in your decision-making process to realize an investment project in the heart of Europe. The Port of Antwerp is a crucial link in a supply chain that connects you to the inner European market and the rest of the world. With an annual volume of more than 200 million tons of maritime freight handled, the extensive storage capacity and the presence of the largest petrochemical cluster in Europe, the Port of Antwerp NADA CA Antwerp is the largest maritime, logistics and ND A A industrial cluster in Europe. US CA RI MEDITE E RR M A A N N E Good nautical access, a dense TI AN LA M of hinterland connections I network D D L E CONNECTING and its geographical location are just E A S T the top three in the list of advantages. / IS C In addition, the Port of Antwerp offers YOUR an attractive investment climate in INVESTMENT IA an innovative environment, with A S USTRALIA/ A a wide range of support, excellent A TO THE WORLD quality of life for expats and a can-do FRICA mentality that pervades the entire port community. N REGIO PACIFIC 2 Investment guide Investment guide 3 oslo Stockholm t ANTWERP Denmark Copenhagen IN WESTERN EUROPE IE NL Dublin Berlin Berlin Amsterdam Great Britain London Antwerp PL Germany Brussels BE Prague Luxembourg CZ 250 km Paris Wien NADA Bern Austria CA Antwerp ND 500 km A A Switzerland Ljubjana US France Zagreb CA RI MEDITE SL E RR HR M A A N N E TI AN LA 750 km BA M ID D L E CONNECTING Italy E A S T / IS Rome C Spain YOUR Madrid INVESTMENT IA A S PT USTRALIA/ A NL Lisbon A TO THE WORLD FRICA Antwerp t ANTWERP IN BELGIUM 45 km Flanders DE N Brussels REGIO PACIFIC BELGIUM Wallonia FR LUX 4 Investment guide 5 Investment guide Investment guide 1 Your choice to invest in the port of Antwerp is We offer you a cluster with room to invest in a future the right one for many reasons.
    [Show full text]
  • Ship-Breaking.Com 2012 Bulletins of Information and Analysis on Ship Demolition, # 27 to 30 from January 1St to December 31St 2012
    Ship-breaking.com 2012 Bulletins of information and analysis on ship demolition, # 27 to 30 From January 1st to December 31st 2012 Robin des Bois 2013 Ship-breaking.com Bulletins of information and analysis on ship demolition 2012 Content # 27 from January 1st to April 15th …..……………………….………………….…. 3 (Demolition on the field (continued); The European Union surrenders; The Senegal project ; Letters to the Editor ; A Tsunami of Scrapping in Asia; The END – Pacific Princess, the Love Boat is not entertaining anymore) # 28 from April 16th to July 15th ……..…………………..……………….……..… 77 (Ocean Producer, a fast ship leaves for the scrap yard ; The Tellier leaves with honor; Matterhorn, from Brest to Bordeaux ; Letters to the Editor ; The scrapping of a Portuguese navy ship ; The India – Bangladesh pendulum The END – Ocean Shearer, end of the cruise for the sheep) # 29 from July 16th to October 14th ....……………………..……………….……… 133 (After theExxon Valdez, the Hebei Spirit ; The damaged ship conundrum; Farewell to container ships ; Lepse ; Letters to the Editor ; No summer break ; The END – the explosion of Prem Divya) # 30 from October 15th to December 31st ….………………..…………….……… 197 (Already broken up, but heading for demolition ; Demolition in America; Falsterborev, a light goes out ; Ships without place of refuge; Demolition on the field (continued) ; Hong Kong Convention; The final 2012 sprint; 2012, a record year; The END – Charlesville, from Belgian Congo to Lithuania) Global Statement 2012 ……………………… …………………..…………….……… 266 Bulletin of information and analysis May 7, 2012 on ship demolition # 27 from January 1 to April 15, 2012 Ship-breaking.com An 83 year old veteran leaves for ship-breaking. The Great Lakes bulker Maumee left for demolition at the Canadian ship-breaking yard at Port Colborne (see p 61).
    [Show full text]
  • MOTIONS of MOORED VESSELS DUE to PASSING VESSELS: FULL-SCALE MEASUREMENTS at a CONTAINER TERMINAL in the PORT of ANTWERP By
    PIANC-World Congress Panama City, Panama 2018 MOTIONS OF MOORED VESSELS DUE TO PASSING VESSELS: FULL-SCALE MEASUREMENTS AT A CONTAINER TERMINAL IN THE PORT OF ANTWERP by S. Ides1, C. Pauwels2 and P. Torfs3 EXTENDED ABSTRACT The North Sea terminal (Figure 1) is a busy container terminal in the port of Antwerp which is located in the tidal river Scheldt along the navigation channel. At this terminal multiple deep-drafted container vessels in the range of Neo Panamax up to Ultra Large Container Vessels berth on weekly basis. On the other hand, all seagoing vessels coming to and leaving the port of Antwerp pass this terminal. All passing vessels cause a displacement of the water resulting in forces working on the moored vessel. The size of these forces are dependent on the water level, the passing speed, the passing distance as well as the dimensions of the passing and the moored vessel (Talstra et al, 2014). The mooring lines as well as the fenders will try to absorb the forces working on the moored vessel, however the latter one will experience some motions due to the elasticity of both mooring lines and fenders. Figure 1: Port of Antwerp – North Sea terminal (north) and Europe terminal (south) located along the river Scheldt. The Zandvliet-Berendrecht lock complex to the non-tidal port area on the right bank is also visible on the figure. ______________________ 1 Antwerp Port Authority, Port Area Development, [email protected] 2 Antwerp Port Authority, Port Area Development, [email protected] 3 Antwerp Port Authority, Vessel Traffic Management, [email protected] 1 PIANC-World Congress Panama City, Panama 2018 The North Sea terminal was designed and built in the 1990’s.
    [Show full text]
  • Port of Antwerp Invests in Top-Notch Infrastructure
    Port of Antwerp invests in top-notch infrastructure It is impossible Between now and 2025 the port of to stand beside Antwerp and the Flemish government ‘’the lock’s massive will be pumping more than 1.6 billion euros into infrastructure. “Large-scale 28m tall concrete projects such as the new lock for the walls without being Deurganck dock and the Liefkenshoek blown away by the rail tunnel will ensure optimal and scale of it. sustainable infrastructure to support further development of the port,” declares Mark Hansford Deputy editor Eddy Bruyninckx, CEO of Antwerp NEW CIVIL ENGINEERING Port Authority. “Continued investment in world-class port infrastructure is essential for a world player such as the port of Antwerp.” Port of Antwerp invests in top-notch infrastructure he port of Antwerp will pass to the new Deurganck cherishes its advantages dock lock, which will be even PANAMA CANAL T and underpins them with deeper than its Berendrecht state-of-the-art infrastructure. cousin. “The construction of AUTHORITY DRAWS The Port Authority currently has the Deurganck dock lock is civil INSPIRATION FROM quite a number of infrastructure engineering on a grand scale. It ANTWERP projects being carried out. In is impossible to stand beside the addition to the Deurganck dock lock’s massive, 28m tall concrete Antwerp Port Authority and the Panama lock and the Liefkenshoek rail walls without being blown away Canal Authority collaborate closely in tunnel there is maintenance work by the scale of it”, says Mark sharing information. The new locks for on bridges, renovation of docks, Hansford, deputy editor of New the Panama canal are based on the locks and port sites, develop- Civil Engineering.
    [Show full text]
  • Title of Paper
    LOCK MANOEUVRES: PRACTICAL CASES IN EUROPE AND PANAMA K Eloot, Flanders Hydraulics Research, Ghent University, Belgium M Vantorre, Ghent University, Belgium J Verwilligen, Flanders Hydraulics Research, Belgium D Bus, R Cleeren and E Gheyle, Flemish Pilotage, Belgium E Veche, Station de Pilotage de Dunkerque, France E Heugen and J van Drongelen, Dutch Pilotage, the Netherlands R Salas, Panama Canal Pilots, Panama R Detienne, Brabo, Belgium SUMMARY Lock manoeuvres are daily practice for the ships in their approach to harbours worldwide. The experiences of five pilotages operating in Europe (Belgium, France and the Netherlands) and Panama are brought together in a paper describing the operation of pilots in the entrances to and in the locks. A division is made concerning locks with approach walls at one or both sides of the lock and locks without approach walls. The lock construction and the approach areas are described and compared for the locks in Panama, in Dunkirk (Charles de Gaulle lock), in Terneuzen (West lock) and in Antwerp (Berendrecht lock). Correspondence between the lock manoeuvres and the use of tugs can be recognised and shows that lock effects must be overcome by developing and maintaining a good strategy in pilotage which can be shared all over the world. 1. INTRODUCTION techniques are widely used by institutes as a research tool and by pilotages as a training tool. Transfer of Lock manoeuvres are daily practice for ships in their knowledge and expertise helps in defining the similarities approach to the Flemish harbours. The Berendrecht lock and differences between lock operations in Europe and – the largest lock in the world – receives Ultra Large Panama and how to speed up the accessibility issue Container Ships from the Mediterrean Shipping making use of the research results and the operational Company on their way to the Delwaide dock.
    [Show full text]
  • Notices to Mariners No
    Vlaanderen is maritiem Notices to Mariners No. 01 07 JANUARY 2021 NOTICES: 001-078 www.flemishhydrography.be Positions are given in the reference system World Geodetic System 84 (WGS84). Incorrect interpretation of the reference system can lead to errors in the position of several hundred of metres. Depths (in metres): are reduced to Lowest Astronomical Tide (LAT) for tidal areas and to local dock datum for non-tidal areas. Heights (in metres): drying heights are above LAT. Vertical clearance is above Mean High Water Spring (MHWS). Other heights are above Mean Sea Level (MSL). Heights for non-tidal areas are above local dock datum. Directions, bearings, leading lines and light sectors (in degrees) are true reckoned from seawards. NOTICES TO MARINERS No. 01 07 JANUARY 2021 Notices: 001-078 This is a free translation of the official “Berichten aan Zeevarenden, nr. 01 jaargang 2021” In case of dispute the Dutch text is the only valid copy. www.flemishhydrography.be Contents 1/1 NOTICES TO MARINERS 5 1/2 REGULATIONS 6 1/3 OFFICIAL RADIO MESSAGES INTENDED FOR BELGIAN MERCHANT VESSELS: THE BELMAR SYSTEM 7 1/4 BELGIAN COAST STATION OSTEND RADIO - CALLSIGN : OSU - FREQUENCIES, BROADCASTS AND LISTENING OUT 10 1/5 ISPS REGULATIONS 12 1/6 INTERNATIONAL SANITARY REGULATIONS 14 1/7 NAVAL COOPERATION AND GUIDANCE FOR SHIPPING (NCAGS) 15 1/8 RADIO NAVIGATION MESSAGES 19 1/9 RIVER INFORMATION SERVICES 19 1/10 COASTAL-WEATHER-FORECAST 19 1/11 WEATHER FORECASTS AND ANNOUNCEMENTS OF STORMY WEATHER AND GALE FORCE WINDS 20 1/12 GNB MANAGEMENT AREA: PROCEDURE
    [Show full text]