Analysis of MIRO/Rosetta Data
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Stardust Comet Flyby
NATIONAL AERONAUTICS AND SPACE ADMINISTRATION Stardust Comet Flyby Press Kit January 2004 Contacts Don Savage Policy/Program Management 202/358-1727 NASA Headquarters, Washington DC Agle Stardust Mission 818/393-9011 Jet Propulsion Laboratory, Pasadena, Calif. Vince Stricherz Science Investigation 206/543-2580 University of Washington, Seattle, WA Contents General Release ……………………………………......………….......................…...…… 3 Media Services Information ……………………….................…………….................……. 5 Quick Facts …………………………………………..................………....…........…....….. 6 Why Stardust?..................…………………………..................………….....………......... 7 Other Comet Missions ....................................................................................... 10 NASA's Discovery Program ............................................................................... 12 Mission Overview …………………………………….................……….....……........…… 15 Spacecraft ………………………………………………..................…..……........……… 25 Science Objectives …………………………………..................……………...…........….. 34 Program/Project Management …………………………...................…..…..………...... 37 1 2 GENERAL RELEASE: NASA COMET HUNTER CLOSING ON QUARRY Having trekked 3.2 billion kilometers (2 billion miles) across cold, radiation-charged and interstellar-dust-swept space in just under five years, NASA's Stardust spacecraft is closing in on the main target of its mission -- a comet flyby. "As the saying goes, 'We are good to go,'" said project manager Tom Duxbury at NASA's Jet -

Achievements of Hayabusa2: Unveiling the World of Asteroid by Interplanetary Round Trip Technology
Achievements of Hayabusa2: Unveiling the World of Asteroid by Interplanetary Round Trip Technology Yuichi Tsuda Project Manager, Hayabusa2 Japan Aerospace ExplorationAgency 58th COPUOS, April 23, 2021 Lunar and Planetary Science Missions of Japan 1980 1990 2000 2010 2020 Future Plan Moon 2007 Kaguya 1990 Hiten SLIM Lunar-A × Venus 2010 Akatsuki 2018 Mio 1998 Nozomi × Planets Mercury (Mars) 2010 IKAROS Venus MMX Phobos/Mars 1985 Suisei 2014 Hayabusa2 Small Bodies Asteroid Ryugu 2003 Hayabusa 1985 Sakigake Asteroid Itokawa Destiny+ Comet Halley Comet Pheton 2 Hayabusa2 Mission ✓ Sample return mission to a C-type asteroid “Ryugu” ✓ 5.2 billion km interplanetary journey. Launch Earth Gravity Assist Ryugu Arrival MINERVA-II-1 Deployment Dec.3, 2014 Sep.21, 2018 Dec.3, 2015 Jun.27, 2018 MASCOT Deployment Oct.3, 2018 Ryugu Departure Nov.13.2019 Kinetic Impact Earth Return Second Dec.6, 2020 Apr.5, 2019 Target Markers Orbiting Touchdown Sep.16, 2019 Jul,11, 2019 First Touchdown Feb.22, 2019 MINERVA-II-2 Orbiting MD [D VIp srvlxp #534<# Oct.2, 2019 Hayabusa2 Spacecraft Overview Deployable Xband Xband Camera (DCAM3) HGA LGA Xband Solar Array MGA Kaba nd Ion Engine HGA Panel RCS thrusters ×12 ONC‐T, ONC‐W1 Star Trackers Near Infrared DLR MASCOT Spectrometer (NIRS3) Lander Thermal Infrared +Z Imager (TIR) Reentry Capsule +X MINERVA‐II Small Carry‐on +Z LIDAR ONC‐W2 +Y Rovers Impactor (SCI) +X Sampler Horn Target +Y Markers ×5 Launch Mass: 609kg Ion Engine: Total ΔV=3.2km/s, Thrust=5-28mN (variable), Specific Impulse=2800- 3000sec. (4 thrusters, mounted on two-axis gimbal) Chemical RCS: Bi-prop. -

MIT Japan Program Working Paper 01.10 the GLOBAL COMMERCIAL
MIT Japan Program Working Paper 01.10 THE GLOBAL COMMERCIAL SPACE LAUNCH INDUSTRY: JAPAN IN COMPARATIVE PERSPECTIVE Saadia M. Pekkanen Assistant Professor Department of Political Science Middlebury College Middlebury, VT 05753 [email protected] I am grateful to Marco Caceres, Senior Analyst and Director of Space Studies, Teal Group Corporation; Mark Coleman, Chemical Propulsion Information Agency (CPIA), Johns Hopkins University; and Takashi Ishii, General Manager, Space Division, The Society of Japanese Aerospace Companies (SJAC), Tokyo, for providing basic information concerning launch vehicles. I also thank Richard Samuels and Robert Pekkanen for their encouragement and comments. Finally, I thank Kartik Raj for his excellent research assistance. Financial suppport for the Japan portion of this project was provided graciously through a Postdoctoral Fellowship at the Harvard Academy of International and Area Studies. MIT Japan Program Working Paper Series 01.10 Center for International Studies Massachusetts Institute of Technology Room E38-7th Floor Cambridge, MA 02139 Phone: 617-252-1483 Fax: 617-258-7432 Date of Publication: July 16, 2001 © MIT Japan Program Introduction Japan has been seriously attempting to break into the commercial space launch vehicles industry since at least the mid 1970s. Yet very little is known about this story, and about the politics and perceptions that are continuing to drive Japanese efforts despite many outright failures in the indigenization of the industry. This story, therefore, is important not just because of the widespread economic and technological merits of the space launch vehicles sector which are considerable. It is also important because it speaks directly to the ongoing debates about the Japanese developmental state and, contrary to the new wisdom in light of Japan's recession, the continuation of its high technology policy as a whole. -

Japanese Reflections on World War II and the American Occupation Japanese Reflections on World War II and the American Occupation Asian History
3 ASIAN HISTORY Porter & Porter and the American Occupation II War World on Reflections Japanese Edgar A. Porter and Ran Ying Porter Japanese Reflections on World War II and the American Occupation Japanese Reflections on World War II and the American Occupation Asian History The aim of the series is to offer a forum for writers of monographs and occasionally anthologies on Asian history. The Asian History series focuses on cultural and historical studies of politics and intellectual ideas and crosscuts the disciplines of history, political science, sociology and cultural studies. Series Editor Hans Hägerdal, Linnaeus University, Sweden Editorial Board Members Roger Greatrex, Lund University Angela Schottenhammer, University of Salzburg Deborah Sutton, Lancaster University David Henley, Leiden University Japanese Reflections on World War II and the American Occupation Edgar A. Porter and Ran Ying Porter Amsterdam University Press Cover illustration: 1938 Propaganda poster “Good Friends in Three Countries” celebrating the Anti-Comintern Pact Cover design: Coördesign, Leiden Lay-out: Crius Group, Hulshout Amsterdam University Press English-language titles are distributed in the US and Canada by the University of Chicago Press. isbn 978 94 6298 259 8 e-isbn 978 90 4853 263 6 doi 10.5117/9789462982598 nur 692 © Edgar A. Porter & Ran Ying Porter / Amsterdam University Press B.V., Amsterdam 2017 All rights reserved. Without limiting the rights under copyright reserved above, no part of this book may be reproduced, stored in or introduced into a retrieval system, or transmitted, in any form or by any means (electronic, mechanical, photocopying, recording or otherwise) without the written permission of both the copyright owner and the author of the book. -

JAXA's Planetary Exploration Plan
Planetary Exploration and International Collaboration Institute of Space and Astronautical Science Japan Aerospace Exploration Agency Yoshio Toukaku, Director for International Strategy and Coordination Naoya Ozaki, Assistant Professor, Dept of Spacecraft Engineering ISAS/JAXA September, 2019 The Path Japanese Planetary Exploration 1985 1995 2010 2018 Sakigake/ Nozomi Akatsuki BepiColombo Suisei MMO/MPO Comet flyby Planned and Venus Climate Mercury Orbiter launched Mars Orbiter orbiter Asteroid Sample Asteroid Sample Martian Moons Lunar probe Return Mission Return Mission explorer Hiten Hayabusa Hayabusa2 MMX 1992 2003 2014 2020s (TBD) Recent Science Missions HAYABUSA 2003-2010 HINODE(SOLAR-B)2006- KAGUYASELENE)2007-2009 Asteroid Explorer SolAr OBservAtion Lunar Exploration AKATSUKI 2010- Venus Meteorology IKAROS 2010 HisAki 2013 SolAr SAil PlAnetary atmosphere HAYABUSA2 2014-2020 Hitomi(ASTRO-H) 2016 ArAse (ERG) 2016 Asteroid Explorer X-Ray Astronomy Van Allen Belt proBe Hayabusa & Hayabusa 2 Asteroid Sample Return Missions “Hayabusa” spacecraft brought back the material of Asteroid Itokawa while establishing innovative ion engines. “Hayabusa2”, while utilizing the experience cultivated in “Hayabusa”, has arrived at the C type Asteroid Ryugu in order to elucidate the origin and evolution of the solar system and primordial materials that would have led to emergence of life. Hayabusa Hayabusa2 Target Itokawa Ryugu Launch 2003 2014 Arrival 2005 2018 Return 2010 2020 ©JAXA Asteroid Ryugu 6 Martian Moons eXploration (MMX) Sample return from Marian moon for detailed analysis. Strategic L-Class A key element in the ISAS roadmap for small body exploration. Phase A n Science Objectives 1. Origin of Mars satellites. - Captured asteroids? - Accreted debris resulting from a giant impact? 2. Preparatory processes enabling to the habitability of the solar system. -

Japan's Asteroid Missions Hayabusa and Hayabusa2
Japan's Asteroid Missions Hayabusa and Hayabusa2 COPUOS 2013 February 15, 2013, Vienna, Austria Makoto Yoshikawa Hayabusa & Hayabusa2 Project Team, JAXA Lunar and Planetary Missions of Japan ×LUNAR- Hiten A ×Nozom Moon IKAROS 1985 i Moon Sakigake Kaguya 1990 Mars △Akatsuki 1998 Moon Suisei 2003 Hayabusa Venus 2007 BepiColombo 2010 2014 Comet Halley Asteroid Itokawa Hayabusa2 Mercury Asteroid 1999 JU3 February 15, 2013 COPUOS 2013 2 Challenges of Hayabusa and Hayabusa2 Development of the technology for asteroid sample return •Ion engine •Autonomous navigation •Sample collection system •Reentry capsule Impactor system * Study of the origin and evolution of the solar system Molecular cloud Proto solar system disk Solar system Evolution of planets Minerals, H 2O *, Organic matters * (*Hayabusa2) February 15, 2013 COPUOS 2013 3 History of Hayabusa and Hayabusa2 Idea for sample Serious troubles return began in1985 in Hayabusa Now Year 200 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 0 Sample MUSES-C Hayabusa Analysis ▲ ▲ launch Earth return project Started Hayabusa Mk2 in 1996 Post MUSES-C Post Hayabusa Post Marco Polo Haybusa2 Launch Hyabusa2 Phase-B ▲ Initial proposal in 2006 New proposal in 2009 Copy of Hayabusa but modified Modified Hayabusa adding new challenges Target : C-type asteroid 1999 JU3 Target : C-type asteroid 1999 JU3 Launch: 2010 Launch: 2014 February 15, 2013 COPUOS 2013 4 Starting point of Hayabusa Small Meeting for Asteroid Sample Return Mission ISAS June 29, 1985 Cover of meeting February 15, 2013 COPUOS 2013 5 Mission Scenario of Hayabusa Observations, sampling Earth Swingby Launch 19 May 2004 9 May 2003 Asteroid Arrival 12 Sept. -

Çin Ve Japon Mitolojisi
Dönâld A. Mackenzie China and Japnn. Myths and Legends © İmge Kitabevi Yayınları, 1995 Bu çevirinin tüm hakları saklıdır. ISBN 975-533-155-7 1. Baskı: Nisan 1996 Yayıma Hazırlayan Kubilay Aysevener Kapak Tasarımı Fatma Korkut Dizgi İmge Ajans Kapak Baskısı Pelin Ofset 418 70 93 İç Baskı ve Cilt Zirve Ofset 229,66 84 îmge Kitabevi Yayıncılık Paz. San. ve Tic. Ltd. Şti. Konur Sok. No: 3 Kızılay 06650 Ankara Tel: (90 312) 419 46 10 - 419 46 11 Faks: (90 312) 425 65 32 İÇİNDEKİLER Önsöz........................................................................................7 I. .Medeniyetin Doğuşu.......................................................... 11 II. Uzaklara Ulaşan Bir İcat.....................................................21 III. İlk Denizciler ve Kaşifler....................................................30 IV. Dünya Çapmcla Zenginlik Arayışı....................................4ü, V. Çin Ejderha. Bilimi................................................................49 VI. Kuş ve Yılan Mitleri..............................................................65 VII. Ejderha Halk Hikayeleri......................................................73 VIII. Deniz Altındaki Krallık ....................................................... 88 IX. Kutsal Adalar.........................................................................97 X. Çin Ve Japonya'nın Ana Tanrıçası.......................... '...... 116 XI. Ağaç, Ot ve Taş Bilimi...................................................... 338 XII. Bakır Kültürü Çin’e Nasıl Ulaştı?.......;.............................162 -
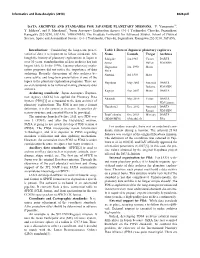
Data Archives and Standards for Japanese Planetary Missions
Informatics and Data Analytics (2018) 6026.pdf DATA ARCHIVES AND STANDARDS FOR JAPANESE PLANETARY MISSIONS. Y. Yamamoto1,2, Y. Ishihara1, and S. Murakami1, 1Japan Aerospace Exploration Agency (3-1-1 Yoshinodai, Chuo-ku, Sagamihara, Kanagawa 252-5210, JAPAN). 2SOKENDAI, The Graduate University for Advanced Studies, School of Physical Science, Space and Aeronautical Science (3-1-1 Yoshinodai, Chuo-ku, Sagamihara, Kanagawa 252-5210, JAPAN). Introduction: Considering the long-term preser- Table 1 Data of Japanese planetary explorers vation of data, it is important to follow standards. Alt- Name Launch Target Archives hough the history of planetary explorations in Japan is Sakigake Jan.1985 Comet DARTS over 30 years, standardization of data archives has just Suisei Halley PDS/SBN begun(Table 1). In the 1990s, Japanese planetary explo- Hagoromo Jan. 1990 Moon - ration programs did not notice the importance of data Hiten archiving. Recently discussions of data archives be- Nozomi Jul. 1998 Mars - come active, and long-term preservation is one of the topics in the planetary exploration programs. There are Hayabusa May 2003 Asteroid DARTS several standards to be followed making planetary data Itokawa PDS/SBN archives. Kaguya Sep. 2007 Moon DARTS Archiving standards: Japan Aerospace Explora- tion Agency (JAXA) has applied the Planetary Data Akatsuki May 2010 Venus DARTS System (PDS)[1] as a standard to the data archives of PDS/Atmos. planetary explorations. The PDS is not just a format Hayabusa2 Dec. 2012 Asteroid DARTS definition, it is the system as its name. It specifies di- Ryugu PDS/SBN rectory structure and essential files to be provided. BepiColombo Oct. -

Distribution and Status of the Introduced Red-Eared Slider (Trachemys Scripta Elegans) in Taiwan 187 T.-H
Assessment and Control of Biological Invasion Risks Compiled and Edited by Fumito Koike, Mick N. Clout, Mieko Kawamichi, Maj De Poorter and Kunio Iwatsuki With the assistance of Keiji Iwasaki, Nobuo Ishii, Nobuo Morimoto, Koichi Goka, Mitsuhiko Takahashi as reviewing committee, and Takeo Kawamichi and Carola Warner in editorial works. The papers published in this book are the outcome of the International Conference on Assessment and Control of Biological Invasion Risks held at the Yokohama National University, 26 to 29 August 2004. The designation of geographical entities in this book, and the presentation of the material, do not imply the expression of any opinion whatsoever on the part of IUCN concerning the legal status of any country, territory, or area, or of its authorities, or concerning the delimitation of its frontiers or boundaries. The views expressed in this publication do not necessarily reflect those of IUCN. Publication of this book was aided by grants from the 21st century COE program of Japan Society for Promotion of Science, Keidanren Nature Conservation Fund, the Japan Fund for Global Environment of the Environmental Restoration and Conservation Agency, Expo’90 Foundation and the Fund in the Memory of Mr. Tomoyuki Kouhara. Published by: SHOUKADOH Book Sellers, Japan and the World Conservation Union (IUCN), Switzerland Copyright: ©2006 Biodiversity Network Japan Reproduction of this publication for educational or other non-commercial purposes is authorised without prior written permission from the copyright holder provided the source is fully acknowledged and the copyright holder receives a copy of the reproduced material. Reproduction of this publication for resale or other commercial purposes is prohibited without prior written permission of the copyright holder. -

Pos(RTS2012)011
Space-VLBI as seen from Japan Hisashi Hirabayashi The Institute of Space and Astronautical Science PoS(RTS2012)011 Japan Aerospace Exploration Agency #-1-1, Yoshinodai, sagamihara,Kanagawa, 229-8510 Japan E-mail: [email protected] Abstract Space-VLBI started to be talked about in 1980s as a small test ISAS mission with small existing launcher. The idea evolved into a larger program with new ISAS launcher development, significant collaboration with NASA Jet Propulsion Laboratory, and with world wide collaborations with ground VLBI facilities. Space-VLBI needed good international coordination, and frameworks for its complex operation were established. IACG (Inter-Agency Consultative Group of Space Science) Panel-1 for Radio Astronomy was formed from space- agencies side, and GVWG (Global VLBI Working Group) was formed from radio astronomy side. And the Japanese VSOP (VLBI Space Observatory Programme) mission formed VISC, VSOG, etc for the mission as were suggested by the guideline. Richard Schilizzi, with his experience and wisdom contributed in many ways in these activities.. Early stage of Japanese space-VLBI planning Nobeyama Radio Observatory was dedicated for mm-wave radio astronomy and was opened in 1982. Using the 45m radio telescope as a very sensitive element for mm-VLBI and targeting to active galactic nuclei was planned. Small VLBI group started to work on this. After confirming 1.3cm fringes with the help of Haystack Radio Observatory, coherency checks were carefully done at Nobeyama 45m telescope, and first international 7mm fringes with Nobeyama was obtained in 1986, and the first 3mm international fringes with Nobeyama followed in 1988. -

Inter-Agency Consultative Group for Space Science (IACG) Handbook Of
Inter-Agency Consultative Group for Space Science (IACG) Handbook of Missions and Payloads May 1994 Inter-Agency Consultative Group (IACG) Handbook of IACG Missions and Payloads May 1994 Table of Contents Introduction ..................................................................................................................... iii Advanced Composition Explorer (ACE) ......................................................................... 1 Akebono ........................................................................................................................... 6 APEX ............................................................................................................................. 11 Cluster ............................................................................................................................ 13 CORONAS .................................................................................................................... 19 Fast ................................................................................................................................. 23 Galileo ............................................................................................................................ 25 Geotail ............................................................................................................................ 36 GOES ............................................................................................................................. 40 Interball ......................................................................................................................... -
![Arxiv:1803.07022V2 [Astro-Ph.EP] 11 Apr 2018 Ment](https://docslib.b-cdn.net/cover/7960/arxiv-1803-07022v2-astro-ph-ep-11-apr-2018-ment-3097960.webp)
Arxiv:1803.07022V2 [Astro-Ph.EP] 11 Apr 2018 Ment
DRAFT VERSION APRIL 12, 2018 Preprint typeset using LATEX style emulateapj v. 12/16/11 THE FEASIBILITY AND BENEFITS OF IN SITU EXPLORATION OF ‘OUMUAMUA-LIKE OBJECTS DARRYL SELIGMAN1 ,GREGORY LAUGHLIN1 , Draft version April 12, 2018 ABSTRACT A rapid accumulation of observations and interpretation have followed in the wake of 1I ‘Oumuamua’s passage through the inner Solar System. We briefly outline the consequences that this first detection of an interstellar asteroid implies for the planet-forming process, and we assess the near-term prospects for detecting and observing (both remotely and in situ) future Solar System visitors of this type. Drawing on detailed heat- transfer calculations that take both ‘Oumuamua’s unusual shape and its chaotic tumbling into account, we affirm that the lack of a detectable coma in deep images of the object very likely arises from the presence of a radiation-modified coating of high molecular weight material (rather than a refractory bulk composition). Assuming that ‘Oumuamua is a typical representative of a larger population with a kinematic distribution similar to Population I stars in the local galactic neighborhood, we calculate expected arrival rates, impact parameters and velocities of similar objects and assess their prospects for detection using operational and forthcoming facilities. Using ‘Oumuamua as a proof-of-concept, we assess the prospects for missions that intercept interstellar objects (ISOs) using conventional chemical propulsion. Using a “launch on detection” paradigm, we estimate wait times of order 10 years between favorable mission opportunities with the detection capabilities of the Large-Scale Synoptic Survey Telescope (LSST), a figure that will be refined as the population of interstellar asteroids becomes observationally better constrained.