Improving and Validating Data-Driven Genotypic Interpretation Systems for the Selection of Antiretroviral Therapies
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
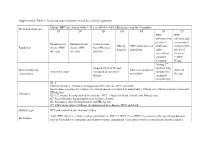
Inclusion and Exclusion Criteria for Each Key Question
Supplemental Table 1: Inclusion and exclusion criteria for each key question Chronic HBV infection in adults ≥ 18 year old (detectable HBsAg in serum for >6 months) Definition of disease Q1 Q2 Q3 Q4 Q5 Q6 Q7 HBV HBV infection with infection and persistent compensated Immunoactive Immunotolerant Seroconverted HBeAg HBV mono-infected viral load cirrhosis with Population chronic HBV chronic HBV from HBeAg to negative population under low level infection infection anti-HBe entecavir or viremia tenofovir (<2000 treatment IU/ml) Adding 2nd Stopped antiviral therapy antiviral drug Interventions and Entecavir compared Antiviral Antiviral therapy compared to continued compared to comparisons to tenofovir therapy therapy continued monotherapy Q1-2: Clinical outcomes: Cirrhosis, decompensated liver disease, HCC and death Intermediate outcomes (if evidence on clinical outcomes is limited or unavailable): HBsAg loss, HBeAg seroconversion and Outcomes HBeAg loss Q3-4: Cirrhosis, decompensated liver disease, HCC, relapse (viral and clinical) and HBsAg loss Q5: Renal function, hypophosphatemia and bone density Q6: Resistance, flare/decompensation and HBeAg loss Q7: Clinical outcomes: Cirrhosis, decompensated liver disease, HCC and death Study design RCT and controlled observational studies Acute HBV infection, children and pregnant women, HIV (+), HCV (+) or HDV (+) persons or other special populations Exclusions such as hemodialysis, transplant, and treatment failure populations. Co treatment with steroids and uncontrolled studies. Supplemental Table 2: Detailed Search Strategy: Ovid Database(s): Embase 1988 to 2014 Week 37, Ovid MEDLINE(R) In-Process & Other Non- Indexed Citations and Ovid MEDLINE(R) 1946 to Present, EBM Reviews - Cochrane Central Register of Controlled Trials August 2014, EBM Reviews - Cochrane Database of Systematic Reviews 2005 to July 2014 Search Strategy: # Searches Results 1 exp Hepatitis B/dt 26410 ("hepatitis B" or "serum hepatitis" or "hippie hepatitis" or "injection hepatitis" or 2 178548 "hepatitis type B").mp. -

Classification Decisions Taken by the Harmonized System Committee from the 47Th to 60Th Sessions (2011
CLASSIFICATION DECISIONS TAKEN BY THE HARMONIZED SYSTEM COMMITTEE FROM THE 47TH TO 60TH SESSIONS (2011 - 2018) WORLD CUSTOMS ORGANIZATION Rue du Marché 30 B-1210 Brussels Belgium November 2011 Copyright © 2011 World Customs Organization. All rights reserved. Requests and inquiries concerning translation, reproduction and adaptation rights should be addressed to [email protected]. D/2011/0448/25 The following list contains the classification decisions (other than those subject to a reservation) taken by the Harmonized System Committee ( 47th Session – March 2011) on specific products, together with their related Harmonized System code numbers and, in certain cases, the classification rationale. Advice Parties seeking to import or export merchandise covered by a decision are advised to verify the implementation of the decision by the importing or exporting country, as the case may be. HS codes Classification No Product description Classification considered rationale 1. Preparation, in the form of a powder, consisting of 92 % sugar, 6 % 2106.90 GRIs 1 and 6 black currant powder, anticaking agent, citric acid and black currant flavouring, put up for retail sale in 32-gram sachets, intended to be consumed as a beverage after mixing with hot water. 2. Vanutide cridificar (INN List 100). 3002.20 3. Certain INN products. Chapters 28, 29 (See “INN List 101” at the end of this publication.) and 30 4. Certain INN products. Chapters 13, 29 (See “INN List 102” at the end of this publication.) and 30 5. Certain INN products. Chapters 28, 29, (See “INN List 103” at the end of this publication.) 30, 35 and 39 6. Re-classification of INN products. -

This Project Has Been Supported with Unrestriced Grants from Abbvie Gilead Sciences HEXAL Janssen-Cilag MSD Viiv Healthcare By
This project has been supported with unrestriced grants from AbbVie Gilead Sciences HEXAL Janssen-Cilag MSD ViiV Healthcare By Marcus Altfeld, Hamburg/Boston (USA) Achim Barmeyer, Dortmund Georg Behrens, Hannover Dirk Berzow, Hamburg Christoph Boesecke, Bonn Patrick Braun, Aachen Thomas Buhk, Hamburg Rob Camp, Barcelona (Spain/USA) Rika Draenert, Munich Christian Eggers, Linz (Austria) Stefan Esser, Essen Gerd Fätkenheuer, Cologne Gunar Günther, Windhoek (Namibia) Thomas Harrer, Erlangen Christian Herzmann, Borstel Christian Hoffmann, Hamburg Heinz-August Horst, Kiel Martin Hower, Dortmund Christoph Lange, Borstel Thore Lorenzen, Hamburg Tim Niehues, Krefeld Christian Noah, Hamburg Ramona Pauli, Munich Ansgar Rieke, Koblenz Jürgen Kurt Rockstroh, Bonn Thorsten Rosenkranz, Hamburg Bernhard Schaaf, Dortmund Ulrike Sonnenberg-Schwan, Munich Christoph D. Spinner, Munich Thomas Splettstoesser (Figures), Berlin Matthias Stoll, Hannover Hendrik Streeck, Essen/Boston (USA) Jan Thoden, Freiburg Markus Unnewehr, Dortmund Mechthild Vocks-Hauck, Berlin Jan-Christian Wasmuth, Bonn Michael Weigel, Schweinfurt Thomas Weitzel, Santiago (Chile) Eva Wolf, Munich HIV 2015/16 www.hivbook.com Edited by Christian Hoffmann and Jürgen K. Rockstroh Medizin Fokus Verlag IV Christian Hoffmann, M.D., Ph.D. ICH Stadtmitte (Infektionsmedizinisches Centrum Hamburg) Glockengiesserwall 1 20095 Hamburg, Germany Phone: + 49 40 2800 4200 Fax: + 49 40 2800 42020 [email protected] Jürgen K. Rockstroh, M.D., Ph.D. Department of Medicine I University of Bonn Sigmund-Freud-Strasse 25 53105 Bonn, Germany Phone: + 49 228 287 6558 Fax: + 49 228 287 5034 [email protected] HIV Medicine is an ever-changing field. The editors and authors of HIV 2015/16 have made every effort to provide information that is accurate and complete as of the date of publication. -

Synthetic Compounds with 2-Amino-1, 3, 4-Thiadiazole Moiety
molecules Review Synthetic Compounds with 2-Amino-1,3,4-Thiadiazole Moiety Against Viral Infections Georgeta Serban Pharmaceutical Chemistry Department, Faculty of Medicine and Pharmacy, University of Oradea, 29 Nicolae Jiga, 410028 Oradea, Romania; [email protected]; Tel.: +4-0756-276-377 Academic Editor: Antonio Carta Received: 29 January 2020; Accepted: 18 February 2020; Published: 19 February 2020 Abstract: Viral infections have resulted in millions of victims in human history. Although great efforts have been made to find effective medication, there are still no drugs that truly cure viral infections. There are currently approximately 90 drugs approved for the treatment of human viral infections. As resistance toward available antiviral drugs has become a global threat to health, there is an intrinsic need to identify new scaffolds that are useful in discovering innovative, less toxic and highly active antiviral agents. 1,3,4-Thiadiazole derivatives have been extensively studied due to their pharmacological profile, physicochemical and pharmacokinetic properties. This review provides an overview of the various synthetic compounds containing the 2-amino-1,3,4-thiadiazole moiety that has been evaluated for antiviral activity against several viral strains and could be considered possible prototypes for the development of new antiviral drugs. Keywords: 2-amino-1,3,4-thiadiazole; viral infections; antiviral agents; drug resistance; inhibitory concentration; mechanism of action 1. Human Viral Infections Viruses are the smallest among -

Phosphinic Acids: Current Status and Potential for Drug Discovery
REVIEWS Drug Discovery Today Volume 24, Number 3 March 2019 Reviews POST SCREEN Phosphinic acids: current status and potential for drug discovery 1,2,3 3,4 2 2 Moaz M. Abdou , Paul M. O’Neill , Eric Amigues and Magdalini Matziari 1 Egyptian Petroleum Research Institute, Nasr City, PO 11727, Cairo, Egypt 2 Department of Chemistry, Xi’an Jiaotong Liverpool University, Suzhou, Jiangsu 215123, PR China 3 Department of Chemistry, University of Liverpool, Liverpool, L69 7ZD, UK 4 Department of Pharmacology, School of Biomedical Sciences, MRC Centre for Drug Safety Science, University of Liverpool, Liverpool, L69 3GE, UK Phosphinic acid derivatives exhibit diverse biological activities and a high degree of structural diversity, rendering them a versatile tool in the development of new medicinal agents. Pronounced recent progress, coupled with previous research findings, highlights the impact of this moiety in medicinal chemistry. Here, we highlight the most important breakthroughs made with phosphinates with a range of pharmacological activities against many diseases, including anti-inflammatory, anti-Alzheimer, antiparasitic, antihepatitis, antiproliferative, anti-influenza, anti-HIV, antimalarial, and antimicrobial agents. We also provide the current status of the corresponding prodrugs, drug-delivery systems, and drug applications of phosphinic acids in the clinical stage Introduction and scope On searching ‘phosphinic acid’ as a keyword in any chemistry The phosphinic acid chemistry story began with the pioneering database; a countless amount of literature references; journal work of August Wilhelm Hofmann in 1855 on methylphosphinic articles; books; and patents appear as proof of its importance acid [1]. The broad biological applications of phosphinic acids are in chemical research; thus; it is impractical to survey the litera- driven by their four combined features: tetrahedral transition state ture of phosphinic acids without narrowing the search to specific resemblance; ability to form electrostatic interactions;, hydrogen perspectives. -

Stembook 2018.Pdf
The use of stems in the selection of International Nonproprietary Names (INN) for pharmaceutical substances FORMER DOCUMENT NUMBER: WHO/PHARM S/NOM 15 WHO/EMP/RHT/TSN/2018.1 © World Health Organization 2018 Some rights reserved. This work is available under the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 IGO licence (CC BY-NC-SA 3.0 IGO; https://creativecommons.org/licenses/by-nc-sa/3.0/igo). Under the terms of this licence, you may copy, redistribute and adapt the work for non-commercial purposes, provided the work is appropriately cited, as indicated below. In any use of this work, there should be no suggestion that WHO endorses any specific organization, products or services. The use of the WHO logo is not permitted. If you adapt the work, then you must license your work under the same or equivalent Creative Commons licence. If you create a translation of this work, you should add the following disclaimer along with the suggested citation: “This translation was not created by the World Health Organization (WHO). WHO is not responsible for the content or accuracy of this translation. The original English edition shall be the binding and authentic edition”. Any mediation relating to disputes arising under the licence shall be conducted in accordance with the mediation rules of the World Intellectual Property Organization. Suggested citation. The use of stems in the selection of International Nonproprietary Names (INN) for pharmaceutical substances. Geneva: World Health Organization; 2018 (WHO/EMP/RHT/TSN/2018.1). Licence: CC BY-NC-SA 3.0 IGO. Cataloguing-in-Publication (CIP) data. -

A Abacavir Abacavirum Abakaviiri Abagovomab Abagovomabum
A abacavir abacavirum abakaviiri abagovomab abagovomabum abagovomabi abamectin abamectinum abamektiini abametapir abametapirum abametapiiri abanoquil abanoquilum abanokiili abaperidone abaperidonum abaperidoni abarelix abarelixum abareliksi abatacept abataceptum abatasepti abciximab abciximabum absiksimabi abecarnil abecarnilum abekarniili abediterol abediterolum abediteroli abetimus abetimusum abetimuusi abexinostat abexinostatum abeksinostaatti abicipar pegol abiciparum pegolum abisipaaripegoli abiraterone abirateronum abirateroni abitesartan abitesartanum abitesartaani ablukast ablukastum ablukasti abrilumab abrilumabum abrilumabi abrineurin abrineurinum abrineuriini abunidazol abunidazolum abunidatsoli acadesine acadesinum akadesiini acamprosate acamprosatum akamprosaatti acarbose acarbosum akarboosi acebrochol acebrocholum asebrokoli aceburic acid acidum aceburicum asebuurihappo acebutolol acebutololum asebutololi acecainide acecainidum asekainidi acecarbromal acecarbromalum asekarbromaali aceclidine aceclidinum aseklidiini aceclofenac aceclofenacum aseklofenaakki acedapsone acedapsonum asedapsoni acediasulfone sodium acediasulfonum natricum asediasulfoninatrium acefluranol acefluranolum asefluranoli acefurtiamine acefurtiaminum asefurtiamiini acefylline clofibrol acefyllinum clofibrolum asefylliiniklofibroli acefylline piperazine acefyllinum piperazinum asefylliinipiperatsiini aceglatone aceglatonum aseglatoni aceglutamide aceglutamidum aseglutamidi acemannan acemannanum asemannaani acemetacin acemetacinum asemetasiini aceneuramic -

Drug Interactions Between Hormonal Contraceptives and Antiretrovirals
Drug interactions between hormonal contraceptives and antiretrovirals Kavita Nandaa, Gretchen S. Stuartb, Jennifer Robinsonc, Andrew L. Grayd, Naomi K. Teppere and Mary E. Gaffieldf Objective: To summarize published evidence on drug interactions between hormonal contraceptives and antiretrovirals. Design: Systematic review of the published literature. Methods: We searched PubMed, POPLINE, and EMBASE for peer-reviewed publi- cations of studies (in any language) from inception to 21 September 2015. We included studies of women using hormonal contraceptives and antiretrovirals concurrently. Outcomes of interest were effectiveness of either therapy, toxicity, or pharmacokinetics. We used standard abstraction forms to summarize and assess strengths and weaknesses. Results: Fifty reports from 46 studies were included. Most antiretrovirals whether used for therapy or prevention, have limited interactions with hormonal contraceptive methods, with the exception of efavirenz. Although depot medroxyprogesterone acetate is not affected, limited data on implants and combined oral contraceptive pills suggest that efavirenz-containing combination antiretroviral therapy may compromise contraceptive effectiveness of these methods. However, implants remain very effective despite such drug interactions. Antiretroviral plasma concentrations and effectiveness are generally not affected by hormonal contraceptives. Conclusion: Women taking antiretrovirals, for treatment or prevention, should not be denied access to the full range of hormonal contraceptive options, but should be counseled on the expected rates of unplanned pregnancy associated with all contra- ceptive methods, in order to make their own informed choices. Copyright Q 2017 The Author(s). Published by Wolters Kluwer Health, Inc. AIDS 2017, 31:917–952 Keywords: antiretroviral therapy, contraceptive implant, depot medroxyprogesterone acetate, HIV, hormonal contraception, systematic review Introduction Decreasing unintended pregnancies also reduces vertical HIV transmission [5]. -

Hoffmann Rockstroh |
Hoffmann| Rockstroh HIV 2015/2016 www.hivbook.com Medizin Fokus Verlag This project has been supported with unrestriced grants from AbbVie Gilead Sciences HEXAL Janssen-Cilag MSD ViiV Healthcare By Marcus Altfeld, Hamburg/Boston (USA) Achim Barmeyer, Dortmund Georg Behrens, Hannover Dirk Berzow, Hamburg Christoph Boesecke, Bonn Patrick Braun, Aachen Thomas Buhk, Hamburg Rob Camp, Barcelona (Spain/USA) Rika Draenert, Munich Christian Eggers, Linz (Austria) Stefan Esser, Essen Gerd Fätkenheuer, Cologne Gunar Günther, Windhoek (Namibia) Thomas Harrer, Erlangen Christian Herzmann, Borstel Christian Hoffmann, Hamburg Heinz-August Horst, Kiel Martin Hower, Dortmund Christoph Lange, Borstel Thore Lorenzen, Hamburg Tim Niehues, Krefeld Christian Noah, Hamburg Ramona Pauli, Munich Ansgar Rieke, Koblenz Jürgen Kurt Rockstroh, Bonn Thorsten Rosenkranz, Hamburg Bernhard Schaaf, Dortmund Ulrike Sonnenberg-Schwan, Munich Christoph D. Spinner, Munich Thomas Splettstoesser (Figures), Berlin Matthias Stoll, Hannover Hendrik Streeck, Essen/Boston (USA) Jan Thoden, Freiburg Markus Unnewehr, Dortmund Mechthild Vocks-Hauck, Berlin Jan-Christian Wasmuth, Bonn Michael Weigel, Schweinfurt Thomas Weitzel, Santiago (Chile) Eva Wolf, Munich HIV 2015/16 www.hivbook.com Edited by Christian Hoffmann and Jürgen K. Rockstroh Medizin Fokus Verlag IV Christian Hoffmann, M.D., Ph.D. ICH Stadtmitte (Infektionsmedizinisches Centrum Hamburg) Glockengiesserwall 1 20095 Hamburg, Germany Phone: + 49 40 2800 4200 Fax: + 49 40 2800 42020 [email protected] Jürgen K. Rockstroh, M.D., Ph.D. Department of Medicine I University of Bonn Sigmund-Freud-Strasse 25 53105 Bonn, Germany Phone: + 49 228 287 6558 Fax: + 49 228 287 5034 [email protected] HIV Medicine is an ever-changing field. The editors and authors of HIV 2015/16 have made every effort to provide information that is accurate and complete as of the date of publication. -

WO 2017/048727 Al 23 March 2017 (23.03.2017) P O P C T
(12) INTERNATIONAL APPLICATION PUBLISHED UNDER THE PATENT COOPERATION TREATY (PCT) (19) World Intellectual Property Organization International Bureau (10) International Publication Number (43) International Publication Date WO 2017/048727 Al 23 March 2017 (23.03.2017) P O P C T (51) International Patent Classification: AO, AT, AU, AZ, BA, BB, BG, BH, BN, BR, BW, BY, A61K 31/519 (2006.01) A61P 31/18 (2006.01) BZ, CA, CH, CL, CN, CO, CR, CU, CZ, DE, DK, DM, DO, DZ, EC, EE, EG, ES, FI, GB, GD, GE, GH, GM, GT, (21) International Application Number: HN, HR, HU, ID, IL, IN, IR, IS, JP, KE, KG, KN, KP, KR, PCT/US20 16/05 1545 KW, KZ, LA, LC, LK, LR, LS, LU, LY, MA, MD, ME, (22) International Filing Date: MG, MK, MN, MW, MX, MY, MZ, NA, NG, NI, NO, NZ, 13 September 2016 (13.09.201 6) OM, PA, PE, PG, PH, PL, PT, QA, RO, RS, RU, RW, SA, SC, SD, SE, SG, SK, SL, SM, ST, SV, SY, TH, TJ, TM, (25) Filing Language: English TN, TR, TT, TZ, UA, UG, US, UZ, VC, VN, ZA, ZM, (26) Publication Language: English ZW. (30) Priority Data: (84) Designated States (unless otherwise indicated, for every 62/218,858 15 September 2015 (15.09.2015) US kind of regional protection available): ARIPO (BW, GH, 62/382,550 1 September 2016 (01.09.2016) US GM, KE, LR, LS, MW, MZ, NA, RW, SD, SL, ST, SZ, TZ, UG, ZM, ZW), Eurasian (AM, AZ, BY, KG, KZ, RU, (71) Applicant: GILEAD SCIENCES, INC. -

1 Anti-HIV Drug Discovery, Development and Synthesis Of
Anti-HIV Drug Discovery, Development and Synthesis of Delavirdine: Review article Wollela Behja1 Mudin Jemal 2 1 Chemistry Department, College of Natural and Computational Sciences, Wolkite University, Ethiopia P.O.Box 07 Wolkite University, Ethiopia 2 Chemistry Department, Natural Sciences College, Jimma University, Ethiopia P.O.Box 378 Jimma University, Ethiopia ABSTRACT Viruses are the smallest infectious agents of animal and plant tissues. Viruses are totally dependent on living cells to survive as they utilize the host cell's own replication processes, in order to reproduce themselves. HIV is the causative agent of AIDS. HIV is an unusually difficult to treat because it incorporate its own genetic material into the genome of an infected host cell. It infects T cells that carry the CD4 antigen on their surface. Binding and fusion, reverse transcription, integration, transcription, assembly and budding are the major steps of the HIV life cycle. The HIV/AIDS disease is treated by interrupting the HIV life cycle with specially designed drugs. The discovery of effective drugs against HIV has focused on targeting various critical components of the replication cycle of HIV. Depending on the target within the HIV replicative cycle they interact with, anti-HIV compounds are categorized into six groups. These are: nucleoside (nucleotide) reverse transcriptase inhibitors (NRTIs), non-nucleoside reverse transcriptase inhibitors (NNRTIs), protease inhibitors (PIs), cell entry inhibitors or fusion inhibitors (FIs), co-receptor inhibitors (CRIs) and integrase inhibitors (INIs). The development of effective anti-HIV drugs is difficult due to wide variations in nucleotide and amino acid sequences. The development of anti-HIV drug passes through several important steps. -

Screening for HIV Infection in Asymptomatic, Nonpregnant Adolescents and Adults: a Systematic Review for the U.S
Evidence Synthesis Number 176 Screening for HIV Infection in Asymptomatic, Nonpregnant Adolescents and Adults: A Systematic Review for the U.S. Preventive Services Task Force Prepared for: Agency for Healthcare Research and Quality U.S. Department of Health and Human Services 5600 Fishers Lane Rockville, MD 20857 www.ahrq.gov Contract No. HHSA-290-2015-00009-I, Task Order No. 7 Prepared by: Pacific Northwest Evidence-Based Practice Center Oregon Health & Science University Mail Code: BICC 3181 SW Sam Jackson Park Road Portland, OR 97239 www.ohsu.edu/epc Investigators: Roger Chou, MD Tracy Dana, MLS Sara Grusing, BA Christina Bougatsos, MPH AHRQ Publication No. 18-05246-EF-1 November 2018 This report is based on research conducted by the Pacific Northwest Evidence-based Practice Center (EPC) under contract to the Agency for Healthcare Research and Quality (AHRQ), Rockville, MD (Contract No. HHSA-290-2015-00009-I, Task Order No. 7). The findings and conclusions in this document are those of the authors, who are responsible for its contents, and do not necessarily represent the views of AHRQ. Therefore, no statement in this report should be construed as an official position of AHRQ or of the U.S. Department of Health and Human Services. The information in this report is intended to help health care decisionmakers—patients and clinicians, health system leaders, and policymakers, among others—make well-informed decisions and thereby improve the quality of health care services. This report is not intended to be a substitute for the application of clinical judgment. Anyone who makes decisions concerning the provision of clinical care should consider this report in the same way as any medical reference and in conjunction with all other pertinent information (i.e., in the context of available resources and circumstances presented by individual patients).