DOCSLIB.ORG

STATISTICAL GRAPHICS and EXPERIMENTAL DATA E. Nikolić

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
STATISTICAL GRAPHICS and EXPERIMENTAL DATA E. Nikolić ICOTS-7, 2006: Nikolic-Doric, Cobanovic and Lozanov-Crvenkovic STATISTICAL GRAPHICS AND EXPERIMENTAL DATA E. Nikoli ć-ðori ć, K. Čobanovi ć, and Z. Lozanov-Crvenkovi ć University of Novi Sad, Serbia and Montenegro [email protected] Statistical graphs are the usual form of visual communication. In the utilization of statistical graphs the emphasis is focused either on the presentation of data or their analysis. The primary function of graphs was the visual presentation of data. But, with the development and application of electronic computers and software the analytical function of graphs has an increasing importance (Schmid, 1983). Today’s graphical techniques allow comparisons between groups of data. Box-and-whisker plot is a simple graphical method that is introduced to students in teaching descriptive statistics as a useful exploratory data analysis tool for studying main characteristics of distribution, detecting outliers and extreme values. This paper deals with application of this diagram and its categorized form (trellis diagram) in analysis and modelling data from designed experiments in agriculture. INTRODUCTION The use of visualization is an essential way of teaching statistics. Preliminary data analysis using graphs should be emphasized in teaching of statistics. Students could very easily, using software possibilities in graphical presentation, get different information and draw conclusions concerning the study matter. The aim of this paper is to propose a way of presenting to students some methods of visualization in the analysis of real data. We will present some examples of the use of Box-Whiskers diagrams based on real data from agricultural practice. Statistical methods, particularly inferential methods, are usually based upon rigidly defined conditions that do not hold in the most practical situations. The most common probabilistic models are based on the often wrong assumption that errors about the deterministic model are normally distributed. Exploratory Data Analysis (EDA) is an alternative approach for data analysis, which employs a variety of techniques, mostly graphical, for data analysis. For EDA the focus is on data, its structure, outliers, extreme values and models suggested by the data. The new developments in computer hardware and software offer many possibilities in graphical presentation of multivariate data by employing sight, sound, colours and movement. The box- and-whisker (box-plot) diagram, introduced by Tukey in 1970, has a useful role in many situations when it is necessary to make preliminary analysis of data ( STATISTICA 7.0, 2004). Very often there exists the need of analyzing data sets according to many different characteristics. The data presented by box plots allow making comparisons between groups or treatments, comparing series of data according to the measures of central tendencies and dispersion, testing hypothesis about treatment means or totals, etc. Concerning the interaction test (Steel and Torrie, 1960), the existence of interaction between different groups or treatments, may be explored by box- plot diagrams. Box plot diagrams may be also used for exploring the normality of data set and the stationarity and seasonality of time series. Box plot diagrams allow ranking of many analyzed sets of data. When a great number of samples or treatments are analyzed, box-plots are very suitable for displaying results of multiple comparison tests, etc. Many authors are emphasizing the need of treatment comparisons by different statistical tests (Montgomery, 1997; Hadživukovi ć and Čobanovi ć, 1994; Čobanovi ć et al ., 2003). In such cases, box-plot diagrams can be very useful in the analysis of data results and in making decisions and conclusions about the tests of hypothesis. Box-plot diagrams, particularly box-whiskers diagrams, are very convenient for the use in the teaching process of basic statistics. The statistical software STATISTICA 7.0 allows for different box-plots diagrams like: Box-Whisker, Whiskers, Boxes, Columns, High-low close. The authors suggest the use of box-whisker diagrams on the base of median, upper and lower quartiles and interquartile range for exploratory data analysis, as they convey information on the central tendency, the spread of the values and tails of distribution. In the case that the data are normally distributed, box-plots on the base of mean value and standard deviation may be used. If the aim is 1 ICOTS-7, 2006: Nikolic-Doric, Cobanovic and Lozanov-Crvenkovic comparison of mean values of several groups, standard error instead of standard deviation is usually preferred. Box-plot may be divided into tiles (known as trellis) and each subset of data may be presented on one tile. Although trellis was developed initially in the context of large data sets it is also useful for modelling data from designed experiments, even small experiments and it is very powerful tool for revealing the structure of interactions (Cleveland and Fuentes, 1997 ). Data analysis using graphical methods in teaching Statistics could be very useful for those students who would continue studies in the research work. The paper offers some examples of a possible use of box-plots diagrams in the teaching of analysis of experiments to students of agriculture. ILLUSTRATIONS We consider the results of field experiment conducted at the Institute for Field and Vegetable Crops in Novi Sad in the period 1994-1998 with three fertilizers (nitrogen, phosphorus and potassium) in three repetitions with nine variants of wheat. In the experiment four quantities of each fertilizer were applied (0, 50, 100, 150 kg/ha) at plots of the same size in 20 out of 64 possible combinations and the yield of wheat (t/ha) was measured. A box-and-whisker diagram on the base of all 2120 experimental data (Figure 1) shows the main characteristics of its distribution. It can be seen that there exists some negative asymmetry as Q1 − Q2 > Q2 − Q3 , where Qi i(, = )3,2,1 is i-th quartile. Also, we see that there are no outliers in the data set. At this point it should be stressed that the box-plot cannot be used for proving normality, but can be used to detect violation of the normality assumptions. Although useful in detecting outliers, the box-plot can hide multimodality. To avoid misinterpretation, it should be explained that the condition Q1 − min X > max X − Q3 , (as met in this case), does not mean that there are more data in the lower part of data when compared to the upper part. Figure 1: Box-whisker plot of yield Figure 2: Box-whisker plots of yield data for levels of first factor Box-plot for each level of a particular variable helps us to make comparisons between subsets of data. Box-plots made for each variant of fertilizer (Figure 2), for all varieties of wheat (Figure 3) and for each year (Figure 4) help us to consider the influence of factors on the experimental units. From these graphs it can be easily seen that the yield of wheat depends on the variant of fertilizer, on the genetic factor and on the weather conditions. The importance of box- and-whisker plot increases when it is used to compare multiple data sets as it allows an easy comparison between the distributions of the data. Box-and-whiskers plots are comparable if subsamples are of the equal size. They may be used for examination if ANOVA assumptions are satisfied (i.e. if groups are roughly symmetric and are of similar spread). It may be seen that the assumptions are not grossly violated although variants 1,3,4,7 exhibit relatively less spread (Figure 2), and data groups in Figures 3 and 4 exhibit a slightly negative asymmetric distribution. 2 ICOTS-7, 2006: Nikolic-Doric, Cobanovic and Lozanov-Crvenkovic Figure 3: Box-whisker plots of yield data for Figure 4: Box-whisker plots of yield data for levels of second factor levels of third factor Categorized box-plot (trellis diagrams), obtained by arranging plots according to specified levels of a given categorical variable, helps in displaying interaction between factors. Taking variety as the variable of interest, categorized box-plots have been created as shown in Figure 5. Figure 5: Trellis box-plots It may be easily seen that the higher yields are obtained for variants 11-20 of fertilizer for all varieties of wheat. The stability of the yield for this variant depends on the variety; it is the least for Rana Niska and the highest for Novosadska Rana, so there exists an interaction between the fertilizer and the variant of wheat. In a similar way, the interaction between a fertilizer and years, years and varieties can be presented. The box-plot may be used for displaying conclusions of multiple comparisons. This is very useful when the number of comparisons is large. On the base of box-plots that contain mean value and corresponding 95% confidence interval for varieties of wheat (Figures 6) it may be concluded that the variants of wheat Balkan, Proteinka, Zvezda are homogeneous as their confidence intervals overlap. The same can be said for the variants Evropa, Italija and Rana niska. Standard errors are calculated using mean-squared error from ANOVA for three-factorial experiment. Similarly, the variants of fertilizer may be compared visually (Figure 7). In the case of unbalanced design or if the assumption of normality is not satisfied, the notched 3 ICOTS-7, 2006: Nikolic-Doric, Cobanovic and Lozanov-Crvenkovic plot may be applied. It consists of notches that are drawn about median on both sides of box-plot and are extended to ± 58,1 ⋅ IQR , where IQR= Q − Q . The notches that do not overlap n 3 1 represent significant difference between medians. Figure 6: Multiple comparisons of varieties of wheat Figure 7: Multiple comparisons of fertilizers CONCLUSION The paper emphasizes that the box-plots diagrams are very useful in preliminary data analysis, since they are very illustrative and simple for interpretation.
Load more

Recommended publications
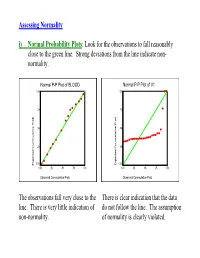
  • Assessing Normality I) Normal Probability Plots : Look for The
    Assessing Normality i) Normal Probability Plots: Look for the observations to fall reasonably close to the green line. Strong deviations from the line indicate non- normality. Normal P-P Plot of BLOOD Normal P-P Plot of V1 1.00 1.00 .75 .75 .50 .50 .25 .25 0.00 0.00 Expected Cummulative Prob Expected Cummulative Expected Cummulative Prob Expected Cummulative 0.00 .25 .50 .75 1.00 0.00 .25 .50 .75 1.00 Observed Cummulative Prob Observed Cummulative Prob The observations fall very close to the There is clear indication that the data line. There is very little indication of do not follow the line. The assumption non-normality. of normality is clearly violated. ii) Histogram: Look for a “bell-shape”. Severe skewness and/or outliers are indications of non-normality. 5 16 14 4 12 10 3 8 2 6 4 1 Std. Dev = 60.29 Std. Dev = 992.11 2 Mean = 274.3 Mean = 573.1 0 N = 20.00 0 N = 25.00 150.0 200.0 250.0 300.0 350.0 0.0 1000.0 2000.0 3000.0 4000.0 175.0 225.0 275.0 325.0 375.0 500.0 1500.0 2500.0 3500.0 4500.0 BLOOD V1 Although the histogram is not perfectly There is a clear indication that the data symmetric and bell-shaped, there is no are right-skewed with some strong clear violation of normality. outliers. The assumption of normality is clearly violated. Caution: Histograms are not useful for small sample sizes as it is difficult to get a clear picture of the distribution.
    [Show full text]
  • Fundamental Statistical Concepts in Presenting Data Principles For
    Fundamental Statistical Concepts in Presenting Data Principles for Constructing Better Graphics Rafe M. J. Donahue, Ph.D. Director of Statistics Biomimetic Therapeutics, Inc. Franklin, TN Adjunct Associate Professor Vanderbilt University Medical Center Department of Biostatistics Nashville, TN Version 2.11 July 2011 2 FUNDAMENTAL STATI S TIC S CONCEPT S IN PRE S ENTING DATA This text was developed as the course notes for the course Fundamental Statistical Concepts in Presenting Data; Principles for Constructing Better Graphics, as presented by Rafe Donahue at the Joint Statistical Meetings (JSM) in Denver, Colorado in August 2008 and for a follow-up course as part of the American Statistical Association’s LearnStat program in April 2009. It was also used as the course notes for the same course at the JSM in Vancouver, British Columbia in August 2010 and will be used for the JSM course in Miami in July 2011. This document was prepared in color in Portable Document Format (pdf) with page sizes of 8.5in by 11in, in a deliberate spread format. As such, there are “left” pages and “right” pages. Odd pages are on the right; even pages are on the left. Some elements of certain figures span opposing pages of a spread. Therefore, when printing, as printers have difficulty printing to the physical edge of the page, care must be taken to ensure that all the content makes it onto the printed page. The easiest way to do this, outside of taking this to a printing house and having them print on larger sheets and trim down to 8.5-by-11, is to print using the “Fit to Printable Area” option under Page Scaling, when printing from Adobe Acrobat.
    [Show full text]
  • Interactive Statistical Graphics/ When Charts Come to Life
    Titel Event, Date Author Affiliation Interactive Statistical Graphics When Charts come to Life [email protected] www.theusRus.de Telefónica Germany Interactive Statistical Graphics – When Charts come to Life PSI Graphics One Day Meeting Martin Theus 2 www.theusRus.de What I do not talk about … Interactive Statistical Graphics – When Charts come to Life PSI Graphics One Day Meeting Martin Theus 3 www.theusRus.de … still not what I mean. Interactive Statistical Graphics – When Charts come to Life PSI Graphics One Day Meeting Martin Theus 4 www.theusRus.de Interactive Graphics ≠ Dynamic Graphics • Interactive Graphics … uses various interactions with the plots to change selections and parameters quickly. Interactive Statistical Graphics – When Charts come to Life PSI Graphics One Day Meeting Martin Theus 4 www.theusRus.de Interactive Graphics ≠ Dynamic Graphics • Interactive Graphics … uses various interactions with the plots to change selections and parameters quickly. • Dynamic Graphics … uses animated / rotating plots to visualize high dimensional (continuous) data. Interactive Statistical Graphics – When Charts come to Life PSI Graphics One Day Meeting Martin Theus 4 www.theusRus.de Interactive Graphics ≠ Dynamic Graphics • Interactive Graphics … uses various interactions with the plots to change selections and parameters quickly. • Dynamic Graphics … uses animated / rotating plots to visualize high dimensional (continuous) data. 1973 PRIM-9 Tukey et al. Interactive Statistical Graphics – When Charts come to Life PSI Graphics One Day Meeting Martin Theus 4 www.theusRus.de Interactive Graphics ≠ Dynamic Graphics • Interactive Graphics … uses various interactions with the plots to change selections and parameters quickly. • Dynamic Graphics … uses animated / rotating plots to visualize high dimensional (continuous) data.
    [Show full text]
  • Infovis and Statistical Graphics: Different Goals, Different Looks1
    Infovis and Statistical Graphics: Different Goals, Different Looks1 Andrew Gelman2 and Antony Unwin3 20 Jan 2012 Abstract. The importance of graphical displays in statistical practice has been recognized sporadically in the statistical literature over the past century, with wider awareness following Tukey’s Exploratory Data Analysis (1977) and Tufte’s books in the succeeding decades. But statistical graphics still occupies an awkward in-between position: Within statistics, exploratory and graphical methods represent a minor subfield and are not well- integrated with larger themes of modeling and inference. Outside of statistics, infographics (also called information visualization or Infovis) is huge, but their purveyors and enthusiasts appear largely to be uninterested in statistical principles. We present here a set of goals for graphical displays discussed primarily from the statistical point of view and discuss some inherent contradictions in these goals that may be impeding communication between the fields of statistics and Infovis. One of our constructive suggestions, to Infovis practitioners and statisticians alike, is to try not to cram into a single graph what can be better displayed in two or more. We recognize that we offer only one perspective and intend this article to be a starting point for a wide-ranging discussion among graphics designers, statisticians, and users of statistical methods. The purpose of this article is not to criticize but to explore the different goals that lead researchers in different fields to value different aspects of data visualization. Recent decades have seen huge progress in statistical modeling and computing, with statisticians in friendly competition with researchers in applied fields such as psychometrics, econometrics, and more recently machine learning and “data science.” But the field of statistical graphics has suffered relative neglect.
    [Show full text]
  • Principles of Graph Construction
    PRINCIPLES OF GRAPH CONSTRUCTION Frank E Harrell Jr Department of Biostatistics Vanderbilt University School of Medicine [email protected] biostat.mc.vanderbilt.edu at Jump: StatGraphCourse Office of Biostatistics, FDA CDER [email protected] Blog: fharrell.com Twitter: @f2harrell DIA/FDA STATISTICS FORUM NORTH BETHESDA MD 2017-04-24 Copyright 2000-2017 FE Harrell All Rights Reserved Chapter 1 Principles of Graph Construction The ability to construct clear and informative graphs is related to the ability to understand the data. There are many excellent texts on statistical graphics (many of which are listed at the end of this chapter). Some of the best are Cleveland’s 1994 book The Elements of Graphing Data and the books by Tufte. The sugges- tions for making good statistical graphics outlined here are heavily influenced by Cleveland’s 1994 book. See also the excellent special issue of Journal of Computa- tional and Graphical Statistics vol. 22, March 2013. 2 CHAPTER 1. PRINCIPLES OF GRAPH CONSTRUCTION 3 1.1 Graphical Perception • Goals in communicating information: reader percep- tion of data values and of data patterns. Both accu- racy and speed are important. • Pattern perception is done by detection : recognition of geometry encoding physi- cal values assembly : grouping of detected symbol elements; discerning overall patterns in data estimation : assessment of relative magnitudes of two physical values • For estimation, many graphics involve discrimination, ranking, and estimation of ratios • Humans are not good at estimating differences with- out directly seeing differences (especially for steep curves) • Humans do not naturally order color hues • Only a limited number of hues can be discriminated in one graphic • Weber’s law: The probability of a human detecting a difference in two lines is related to the ratio of the two line lengths CHAPTER 1.
    [Show full text]
  • Boxplots for Grouped and Clustered Data in Toxicology
    Penultimate version. If citing, please refer instead to the published version in Archives of Toxicology, DOI: 10.1007/s00204-015-1608-4. Boxplots for grouped and clustered data in toxicology Philip Pallmann1, Ludwig A. Hothorn2 1 Department of Mathematics and Statistics, Lancaster University, Lancaster LA1 4YF, UK, Tel.: +44 (0)1524 592318, [email protected] 2 Institute of Biostatistics, Leibniz University Hannover, 30419 Hannover, Germany Abstract The vast majority of toxicological papers summarize experimental data as bar charts of means with error bars. While these graphics are easy to generate, they often obscure essen- tial features of the data, such as outliers or subgroups of individuals reacting differently to a treatment. Especially raw values are of prime importance in toxicology, therefore we argue they should not be hidden in messy supplementary tables but rather unveiled in neat graphics in the results section. We propose jittered boxplots as a very compact yet comprehensive and intuitively accessible way of visualizing grouped and clustered data from toxicological studies together with individual raw values and indications of statistical significance. A web application to create these plots is available online. Graphics, statistics, R software, body weight, micronucleus assay 1 Introduction Preparing a graphical summary is usually the first if not the most important step in a data analysis procedure, and it can be challenging especially with many-faceted datasets as they occur frequently in toxicological studies. However, even in simple experimental setups many researchers have a hard time presenting their results in a suitable manner. Browsing recent volumes of this journal, we have realized that the least favorable ways of displaying toxicological data appear to be the most popular ones (according to the number of publications that use them).
    [Show full text]
  • Statistical Concepts in Metrology — with a Postscript on Statistical Graphics
    NBS Special Publication 747 Statistical Concepts in Metrology — With a Postscript on Statistical Graphics Harry H, Ku NBS NBS NBS NBS NBS NBS NBS NBS NBS NBS iS NBS NBS NBS NBS NBS NBS NBS NBS NBS Nl NBS NBS NBS NBS NBS NBS NBS NBS NBS NBS tS NBS NBS NBS NBS NBS NBS NBS NBS NBS Nl NBS NBS NBS NBS NBS NBS NBS NBS NBS NBS iS NBS NBS NBS NBS NBS NBS NBS NBS NBS NlJ. NBS NBS NBS NBS NBS NBS NBS NBS NBS NBS iS NBS NBS NBS NBS NBS NBS NBS NBS NBS NlJ. NBS NBS NBS NBS NBS NBS NBS NBS NBS NBS tS NBS NBS NBS NBS NBS NBS NBS NBS NBS Nl NBS NBS NBS National Bureau ofStandards NBS NBS tS NBS NBS NBS NBS NBS NBS NBS NBS NBS Nl NBS NBS NBS NBS NBS NBS NBS NBS NBS NBS ^^mS NBS NBS NBS NBS NBS NBS NBS NBS Nl ^^NBS NBS NBS NBS NBS NBS NBS NBS NBS l^mS NBS NBS NBS NBS NBS NBS NBS NBS Nl m he National Bureau of Standards' was established by an act of Congress on March 3, 1901. The m Bureau's overall goal is to strengthen and advance the Nation's science and technology and facilitate their effective application for public benefit. To this end, the Bureau conducts research to assure international competi- tiveness and leadership of U.S. industry, science and technology. NBS work involves development and transfer of measurements, standards and related science and technology, in support of continually improving U.S.
    [Show full text]
  • Length of Stay Outlier Detection Through Cluster Analysis: a Case Study in Pediatrics Daniel Gartnera, Rema Padmanb
    Length of Stay Outlier Detection through Cluster Analysis: A Case Study in Pediatrics Daniel Gartnera, Rema Padmanb aSchool of Mathematics, Cardiff University, United Kingdom bThe H. John Heinz III College, Carnegie Mellon University, Pittsburgh, USA Abstract The increasing availability of detailed inpatient data is enabling the develop- ment of data-driven approaches to provide novel insights for the management of Length of Stay (LOS), an important quality metric in hospitals. This study examines clustering of inpatients using clinical and demographic attributes to identify LOS outliers and investigates the opportunity to reduce their LOS by comparing their order sequences with similar non-outliers in the same cluster. Learning from retrospective data on 353 pediatric inpatients admit- ted for appendectomy, we develop a two-stage procedure that first identifies a typical cluster with LOS outliers. Our second stage analysis compares orders pairwise to determine candidates for switching to make LOS outliers simi- lar to non-outliers. Results indicate that switching orders in homogeneous inpatient sub-populations within the limits of clinical guidelines may be a promising decision support strategy for LOS management. Keywords: Machine Learning; Clustering; Health Care; Length of Stay Email addresses: [email protected] (Daniel Gartner), [email protected] (Rema Padman) 1. Introduction Length of Stay (LOS) is an important quality metric in hospitals that has been studied for decades Kim and Soeken (2005); Tu et al. (1995). However, the increasing digitization of healthcare with Electronic Health Records and other clinical information systems is enabling the collection and analysis of vast amounts of data using advanced data-driven methods that may be par- ticularly valuable for LOS management Gartner (2015); Saria et al.
    [Show full text]
  • Graph Pie — Pie Charts
    Title stata.com graph pie — Pie charts Description Quick start Menu Syntax Options Remarks and examples References Also see Description graph pie draws pie charts. graph pie has three modes of operation. The first corresponds to the specification of two or more variables: . graph pie div1_revenue div2_revenue div3_revenue Three pie slices are drawn, the first corresponding to the sum of variable div1 revenue, the second to the sum of div2 revenue, and the third to the sum of div3 revenue. The second mode of operation corresponds to the specification of one variable and the over() option: . graph pie revenue, over(division) Pie slices are drawn for each value of variable division; the first slice corresponds to the sum of revenue for the first division, the second to the sum of revenue for the second division, and so on. The third mode of operation corresponds to the specification of over() with no variables: . graph pie, over(popgroup) Pie slices are drawn for each value of variable popgroup; the slices correspond to the number of observations in each group. Quick start Pie chart with slices that reflect the proportion of observations for each level of catvar1 graph pie, over(catvar1) As above, but slices reflect the total of v1 for each level of catvar1 graph pie v1, over(catvar1) As above, but with one pie chart for each level of catvar2 graph pie v1, over(catvar1) by(catvar2) Size of slices reflects the share of each variable in the total of v1, v2, v3, v4, and v5 graph pie v1 v2 v3 v4 v5 As above, and label the first slice with its percentage
    [Show full text]
  • Statistical Graphics Using ODS This Document Is an Individual Chapter from SAS/STAT® 13.2 User’S Guide
    SAS/STAT® 13.2 User’s Guide Statistical Graphics Using ODS This document is an individual chapter from SAS/STAT® 13.2 User’s Guide. The correct bibliographic citation for the complete manual is as follows: SAS Institute Inc. 2014. SAS/STAT® 13.2 User’s Guide. Cary, NC: SAS Institute Inc. Copyright © 2014, SAS Institute Inc., Cary, NC, USA All rights reserved. Produced in the United States of America. For a hard-copy book: No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, or otherwise, without the prior written permission of the publisher, SAS Institute Inc. For a Web download or e-book: Your use of this publication shall be governed by the terms established by the vendor at the time you acquire this publication. The scanning, uploading, and distribution of this book via the Internet or any other means without the permission of the publisher is illegal and punishable by law. Please purchase only authorized electronic editions and do not participate in or encourage electronic piracy of copyrighted materials. Your support of others’ rights is appreciated. U.S. Government License Rights; Restricted Rights: The Software and its documentation is commercial computer software developed at private expense and is provided with RESTRICTED RIGHTS to the United States Government. Use, duplication or disclosure of the Software by the United States Government is subject to the license terms of this Agreement pursuant to, as applicable, FAR 12.212, DFAR 227.7202-1(a), DFAR 227.7202-3(a) and DFAR 227.7202-4 and, to the extent required under U.S.
    [Show full text]
  • Graphical Perception: Theory, Experimentation, and Application to the Development of Graphical Methods Author(S): William S
    Graphical Perception: Theory, Experimentation, and Application to the Development of Graphical Methods Author(s): William S. Cleveland and Robert McGill Source: Journal of the American Statistical Association, Vol. 79, No. 387 (Sep., 1984), pp. 531-554 Published by: Taylor & Francis, Ltd. on behalf of the American Statistical Association Stable URL: http://www.jstor.org/stable/2288400 Accessed: 01-03-2016 14:55 UTC Your use of the JSTOR archive indicates your acceptance of the Terms & Conditions of Use, available at http://www.jstor.org/page/ info/about/policies/terms.jsp JSTOR is a not-for-profit service that helps scholars, researchers, and students discover, use, and build upon a wide range of content in a trusted digital archive. We use information technology and tools to increase productivity and facilitate new forms of scholarship. For more information about JSTOR, please contact [email protected]. Taylor & Francis, Ltd. and American Statistical Association are collaborating with JSTOR to digitize, preserve and extend access to Journal of the American Statistical Association. http://www.jstor.org This content downloaded from 162.105.192.28 on Tue, 01 Mar 2016 14:55:50 UTC All use subject to JSTOR Terms and Conditions Graphical Perception: Theory, Experimentation, and Application to the Development of Graphical Methods WILLIAM S. CLEVELAND and ROBERT McGILL* The subject of graphical methods for data analysis and largely unscientific. This is why Cox (1978) argued, for data presentation needs a scientific foundation. In this "There is a major need for a theory of graphical methods" article we take a few steps in the direction of establishing (p.
    [Show full text]
  • Non-Parametric Vs. Parametric Tests in SAS® Venita Depuy and Paul A
    NESUG 17 Analysis Perusing, Choosing, and Not Mis-using: ® Non-parametric vs. Parametric Tests in SAS Venita DePuy and Paul A. Pappas, Duke Clinical Research Institute, Durham, NC ABSTRACT spread is less easy to quantify but is often represented by Most commonly used statistical procedures, such as the t- the interquartile range, which is simply the difference test, are based on the assumption of normality. The field between the first and third quartiles. of non-parametric statistics provides equivalent procedures that do not require normality, but often require DETERMINING NORMALITY assumptions such as equal variances. Parametric tests (OR LACK THEREOF) (which assume normality) are often used on non-normal One of the first steps in test selection should be data; even non-parametric tests are used when their investigating the distribution of the data. PROC assumptions are violated. This paper will provide an UNIVARIATE can be implemented to help determine overview of parametric tests and their non-parametric whether or not your data are normal. This procedure equivalents; what assumptions are required for each test; ® generates a variety of summary statistics, such as the how to perform the tests in SAS ; and guidelines for when mean and median, as well as numerical representations of both sets of assumptions are violated. properties such as skewness and kurtosis. Procedures covered will include PROCs ANOVA, CORR, If the population from which the data are obtained is NPAR1WAY, TTEST and UNIVARIATE. Discussion will normal, the mean and median should be equal or close to include assumptions and assumption violations, equal. The skewness coefficient, which is a measure of robustness, and exact versus approximate tests.
    [Show full text]